基于融合注意力机制LSTM网络的地下水位自适应鲁棒预测

佃松宜，厉潇滢，杨 丹，芮胜阳，郭 斌*

(1.四川大学电气工程学院，四川成都 610065；2.成都兴蓉市政设施管理有限公司，四川成都 610065)

2019年，住房和城乡建设部、生态环境部和发展改革委联合发布了《城镇污水处理提质增效三年行动方案》（2019—2021）[1-2]，方案明确要求进水生化需氧量（BOD）浓度低于100mg/L的污水处理厂应开展系统化整治工作。城市污水管网的降雨入流及地下水入渗问题是污水处理厂进水浓度偏低的重要原因[3]。在实际生活中，旱天外来水入流、入渗水量受管网服务区域排水规律、管道结构条件等复杂因素影响[4]。因此，快速精准地预测地下水水位对预测污水浓度、准确计算旱天污水管网地下水入渗量[5]、辅助管网病害治理与维护具有重要意义。

城市地下水水位除受到降水入流、旱时入渗等因素影响，还受到其所在区域地质层及所铺设管网分布特征制约，导致其水位动态变化，呈现出复杂的非线性、趋势性、季节性、滞后性及随机性等特征[6]，导致其数据的不规律和杂乱性远超其他普通的时间序列数据，其预测面临着独特的挑战和严峻性。在实际水文测量结果中，易出现数据缺失、异常值、非平稳等质量问题[7]；除此之外，水位数据的时空相关性和周期性规律差，难以捕捉，即特征和地下水位间的关联难以被模型挖掘。这系列问题为城市区域级地下水水位预测带来了重大挑战。

目前常用的地下水水位预测方法可大致分为以下3种：基于物理模型的方法[8]、基于时间序列分析的方法[9]和数据驱动的预测方法[10]。基于物理模型的方法是依据地下水流方程和边界条件等物理规律，采用数值方法求解模型预测地下水位。但该方法原理复杂、水文参数定标难、模型开发周期长，还易受假设局限性和不确定性的影响[11]。基于时间序列分析的方法是根据趋势、季节性和周期性[12]等特征，通过对历史数据进行拟合来预测未来的数据[13]，但主要适用于具有周期性和趋势性的数据。以上两种传统的预测方法往往无法充分捕捉地下水位数据中的非线性关系和时空依赖性。基于数据驱动的方法是对已有数据进行学习和分析，通过构建模型完成预测[14]，其原理是基于数据的内在规律和模式识别。例如，杨建飞等[15]通过建立灰色残差模型对宝鸡峡灌区地下水位进行预测，结果显示该模型能够有效克服数据序列不稳定带来的误差并提高预测精度；Barzegar等[16]结合小波变换和神经网络模型对地下水位短期动态进行预测，取得了较为理想的效果。

由于水文数据的特殊性[17]，现有的基于数据驱动的方法不能保证对不同规模数据集的自适应能力[18]。该方法需要大量数据来训练模型，但水文数据常见缺失、异常值等问题，数据质量会影响模型预测的准确性和鲁棒性[19]。其次，数据的时空相关性和周期性并不显著，仅仅使用简单的线性模型或传统的神经网络模型不能够充分挖掘水文特征与地下水位间的关联[20]，无法满足预测的准确性和鲁棒性要求，故选择合适的预测模型尤为重要。随着深度学习模型的迅速发展，越来越多性能良好的模型被提出并被应用于不同的场景，例如长短时记忆网络（LSTM）[21]、门控单元神经网络（GRU）[22]等。其中，LSTM神经网络因方便进行时间序列建模，且具有长期记忆功能，在水位预测方面得到了广泛应用[23–25]。但LSTM网络不能专注于不同时间序列长度的不同变量，在预测过程中不能保证预测效果的鲁棒性[26]。

针对城市地下水位预测中的水位数据随机性与非线性强、时空依赖明显、数据波动规律难捕捉等特点，结合现有预测模型单一、处理时空相关任务弱、灵敏度低、泛化能力弱、鲁棒性能力低等问题，本文提出基于时空注意力机制的LSTM（STA–LSTM）水位预测算法。主要创新点如下：1）基于空间注意力机制快速识别与水位相关联的关键变量，准确捕捉影响地下水位的多因素间的依赖模式和关联性；2）时间注意机制捕捉时间上的依赖关系并自适应地找出不同时间序列长度下与地下水位相关的编码器隐藏状态，可更好捕捉地下水位数据的复杂性和不确定性；3）能够动态地调整权重，提高水位的预测精度，且算法对复杂水位数据有较好的自适应性和较强的鲁棒性，对于城市区域级地下水位预测具有重要的参考价值与工程意义。

1 基于STA–LSTM的水位预测方法

传统的LSTM网络是一种循环神经网络，但相比于原始的循环神经网络的隐层部分，LSTM增加了细胞状态，能保证信息不变地流过整个循环神经网络。LSTM网络还引入门机制用于控制特征的流通和损失，门机制包括输入门、遗忘门和输出门。门能够有选择性地决定让哪些信息通过，通过门机制对细胞状态进行删除或者添加信息。细胞状态和门机制使LSTM网络能够处理长期依赖关系。

本文提出的基于STA–LSTM的自适应鲁棒水位预测方法是在传统LSTM网络的基础之上加入空间注意力机制和时间注意力机制以提高该模型对关键信息的关注程度，主要可分为模型训练阶段和模型预测阶段。在模型训练阶段，基于训练数据计算局部注意力度量并构建相应的地下水位预测模型；在模型预测阶段，利用前一阶段所构建的预测模型进行地下水位预测。

1.1 模型训练阶段

本文提出的STA–LSTM是在传统LSTM网络基础上加入融合注意力机制[27]，其遵循编码器–解码器体系[28]结构，如图1所示。

图1 基于注意力机制的编码器解码器结构Fig. 1 Encoder-decoder structure based on attention mechanism

STA–LSTM首先在编码器中引入空间注意力机制（S–A），可快速识别与水位相关联的关键变量，并为输入变量分配不同的空间注意力值。可变的注意力加权样本数据作为编码器LSTM的新输入。之后，编码器LSTM网络学习新的加权输入的隐藏状态。在第二步中引入时间注意力机制，自适应地找出不同时间序列长度下与地下水位相关的编码器隐藏状态，捕捉时间上的依赖关系。最后，以自适应上下文向量为输入，由另一个解码器LSTM预测输出地下水位的预测值。完整的STA–LSTM算法结构如图2所示。

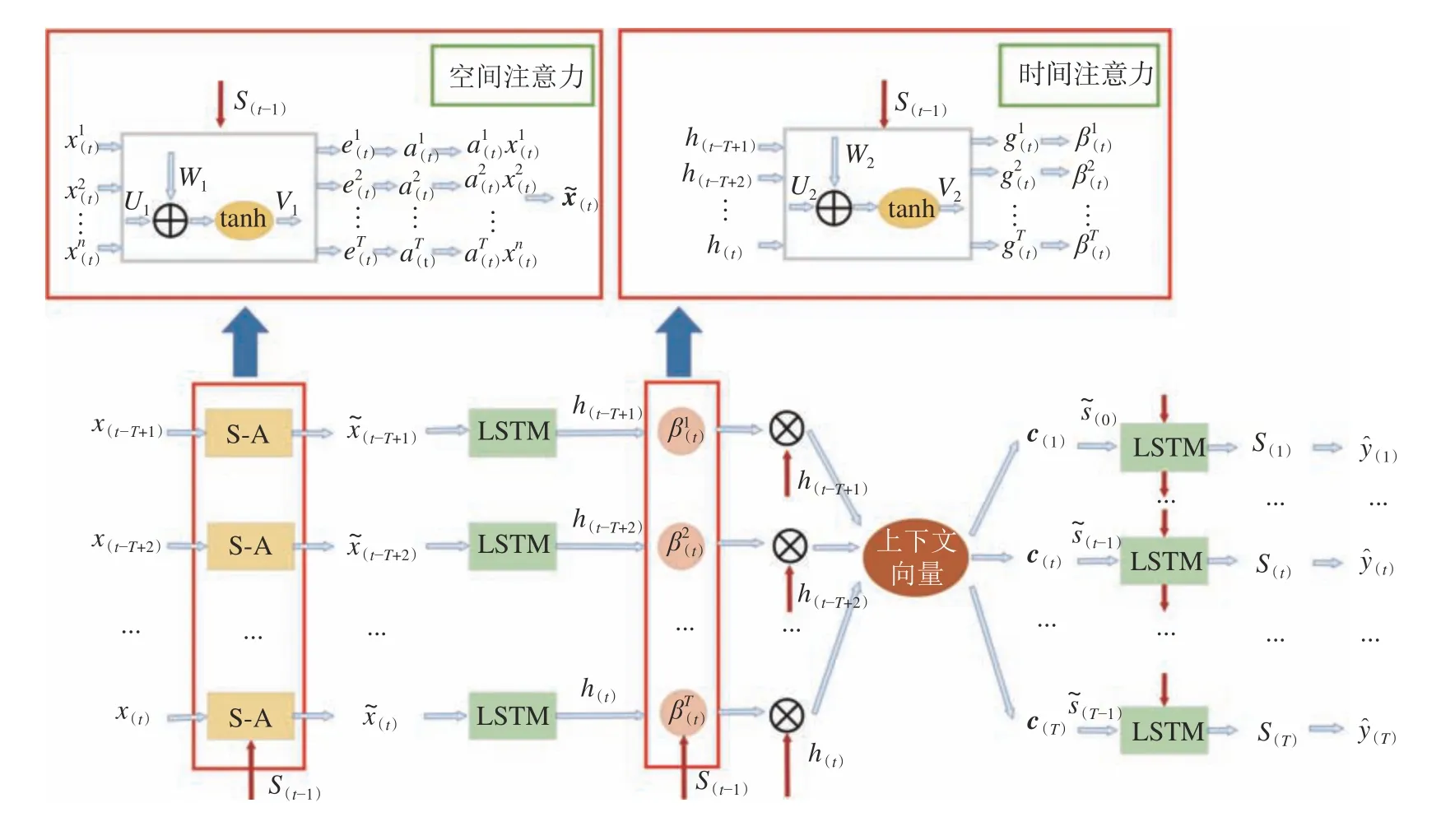
图2 STA–LSTM算法结构Fig. 2 Structure of STA–LSTM algorithm

1.1.1空间注意力机制

由于输入的特征对预测指标影响程度不同，不能简单地给输入特征赋予相同的影响权重，故在算法模型训练阶段提出空间变量注意力机制，可快速识别与水位关联的关键变量。

给定输入序列{x(1),x{(2),···,x(T)}，假设每}个样本有n个输入变量，即x(t)=x1(t),x2(t),···,xn(t)。通过参考先前的解码器隐藏状态获得每个输入变量与地下水位指标之间的关系，通常使用两层网络来获取可变的空间注意力值：

当得到样本x(t)的输入变量空间注意力值时，空间注意力加权样本表示为：

式（4）～（9）中：f(t)、i(t)、o(t)、表示编码器LSTM单元的遗忘门、输入门、输出门和中间状态； ⊙表示两个向量的逐点乘法； σ是非线性sigm oid激活函数；Wf∗、Wo∗、Wi∗、Wc∗、bf、bi、bo、bc是需要学习的参数；m(t)为存储单元。在基于空间注意的LSTM之后，隐藏状态h(t)被用作基于时间注意力机制的LSTM的输入。

1.1.2时间注意力机制

针对不同序列长度对预测效果的影响，设计了自适应时间注意力机制，帮助网络自适应地找出与不同序列长度预测指标相关的编码器隐藏状态，以更好地捕捉时间上的依赖关系。

编码器之后，使用另一个基于LSTM的解码器输出地下水位预测值yˆ(t)。在时间t的隐藏状态时间注意值为：

1.2 模型预测阶段

在模型预测阶段，对于历史水文数据，STA–LSTM网络训练出了最佳参数，网络结构和权重加载到内存中。当把测试集的水文数据输入到训练好的网络中时，STA–LSTM网络利用输入的序列数据，预测出下一个时刻的地下水水位输出。

STA–LSTM预测地下水位的流程如下所示。通过时间反向传播计算参数的梯度，使用Adam算法更新网络参数。

2 实例分析

为了验证基于时空注意力机制的LSTM网络对地下水位预测的有效性，将其应用于水务领域地下水位预测过程中。模拟计算机的配置为：操作系统为W indows10，CPU是Intel(R)Core(TM)i7-8550U CPU@1.80GHz1.99GHz，GPU是NVIDIAGeFo r ce MX 150，RAM为8GB，编码工具为Py t h o n 3.6。

图3为基于时空注意力机制的LSTM网络（STALSTM）预测框架。

图3 STA–LSTM模型框架Fig. 3 STA–LSTM model framework

为比较多种模型的性能，分别建立了GRU、Elman[29]、标准LSTM、VA–LSTM30]、S–LSTM[31]和STA–LSTM。其中，GRU是类似LSTM的递归神经网络，具有更简化的结构和较少的参数，善于在建模长期依赖关系和短期相关性之间实现平衡。Elman循环神经网络借助隐藏层和反馈连接捕捉时序数据的依赖关系；LSTM通过记忆单元和门控机制来捕捉和处理序列数据中的长期依赖关系；VA–LSTM综合了变分自编码器和LSTM的思想，提高模型对不确定数据的建模能力；S–LSTM借助监督机制来捕捉数据间的时序关系和依赖关系。上述方法对水位类时序预测任务进行了研究，同样适用于地下水位的预测任务，将上述算法作为比较算法更具有合理性。选取平均绝对误差(θMAE)、均方根误差(θRMSE)和相关系数( θR2)作为评价指标，θMAE度量预测值和真实值之间的平均差异，且对异常值不敏感、易于解释和计算，能体现模型的鲁棒性；θRMSE度量预测值与真实值之间的均方根误差，对大误差的影响更加敏感； θR2衡量模型对观测数据的解释能力。3个评价指标能够更全面地综合评估模型的鲁棒性和自适应能力，计算方式如下：

式（17）～（19）中，Ttesting为测试样本数，是测试数据中真实值的平均值。

2.1 数据集及数据预处理

意大利小镇Petrignano的地下水位由Chiascio河以及地下含水层提供，本文将STA–LSTM网络应用于预测该镇的地下水水位。地下水水位受降雨量、地下水深度、温度和自来水厂的取水量、Chiascio河的水位参数等的影响。数据时间跨度为2009年1月1日—2020年6月30日。数据来自Acea SmartWater Analytics[32]。输入特征包括降雨量、温度、河水位量、自来水取水量和地下水水位。

在自来水厂取水量和河水位量处出现异常零值时，将其替换成Nan后清除。对于清除后的数据以及缺失数据，选取插值填充的方式。具体的处理结果如图4所示。

数据可视化结果显示除温度外所有特征都具有非恒定的均值和方差。由于动态均值和动态方差的计算均要使用历史数据，动态均值和动态方差从2010年初开始记录，特征平稳性检验结果如图5所示。

本文采取差值处理的方法实现平稳性，以地下水水位的处理效果为例，差值处理过后数据趋于平稳，增广迪基–富勒检验（ADF）数据也证明该序列的平稳性增加，如图6所示。

2.2 结果和讨论

2.2.1参数调整

总共收集了4 199条数据。对于模型训练和测试，用29 4 0个样本组成训练集，剩余1 259个样本为测试数据。对于STA–LSTM，需要优化序列长度参数，候选集合{3，4，5，6}的θMAE、θRMSE和 θR2如图7所示。在该实验中序列长度选择为4，θMAE、θRMSE都取得最小值， θR2取得最大值，此时训练模型达到最佳性能。

除此之外，还需要选择最适合的batchsize，不同的batchsize所对应的详细θMAE、θRMSE和 θR2如图8所示，在batchsize为50时，θMAE、θRMSE都取得最小值， θR2取得最大值，此时模型达到最佳效果。另外，神经网络在空间和时间注意力机制都是两层神经网络。

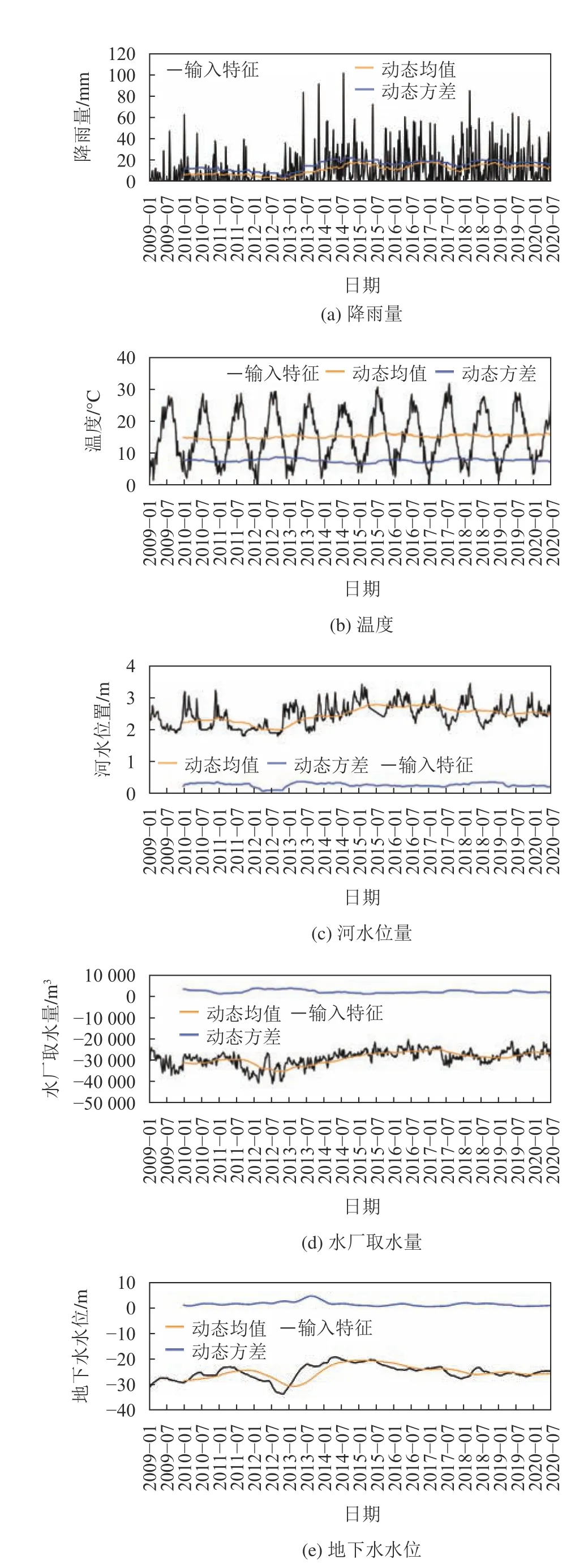
图5 特征平稳性检验Fig.5 Feature Stationarity test diagram

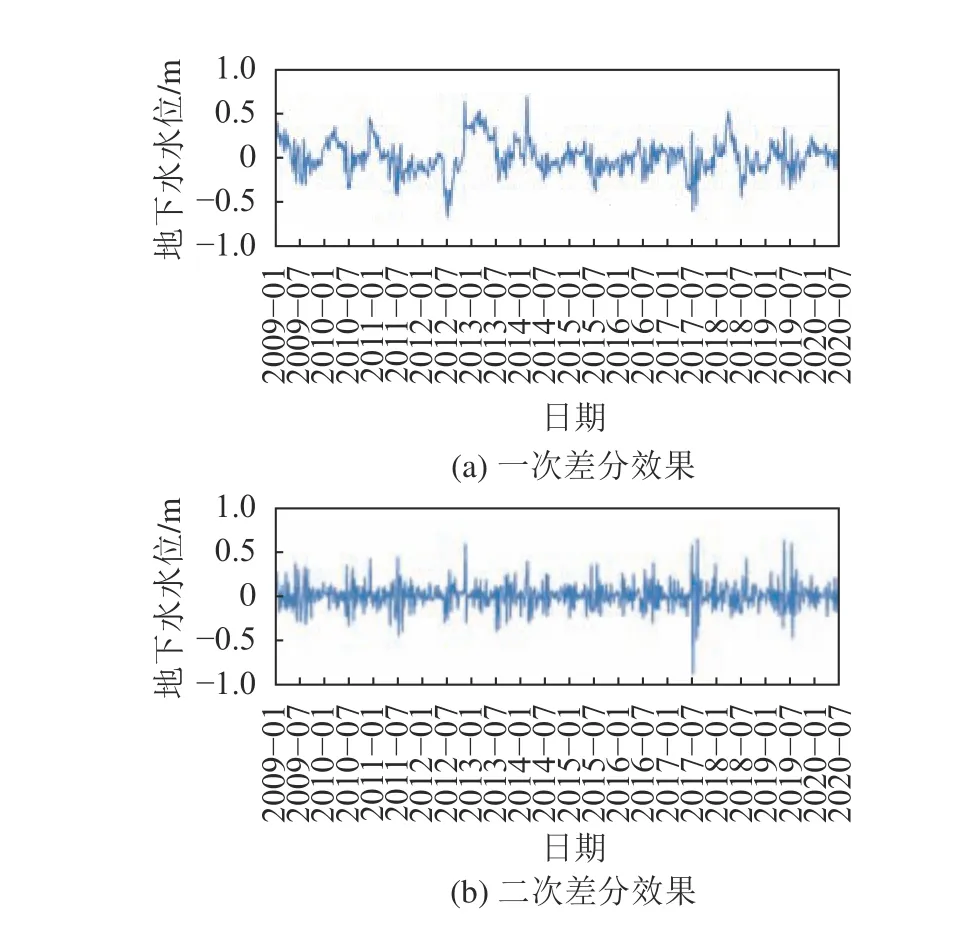
图6 差值处理实现平稳效果Fig.6 Effect of difference processing to achieve stability

图7 评价指标与序列长度之间的关系Fig.7 Relationship between evaluation index and sequence length

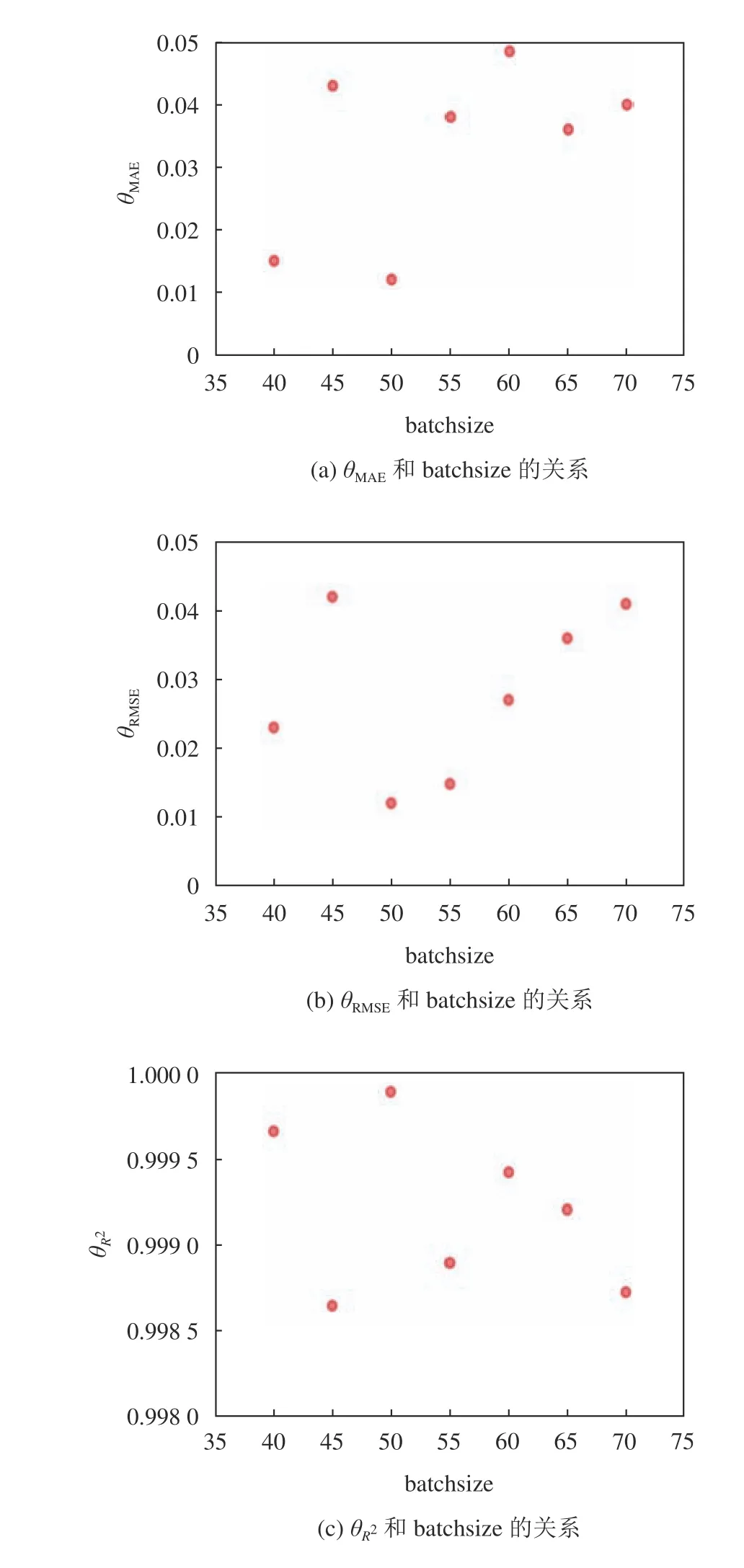
图8 评价指标与batchsize之间的关系Fig. 8 Relationship between evaluation index and batchsize

2.2.2模型有效性验证

为了证明模型的有效性，有必要验证该模型的结构和参数。因此对该模型进行了一些统计测试，如残差自相关（ACF）以及残差偏自相关（PACF）。

式（20）～（21）中，自相关函数的Cov(Xt,Xt–k)是时间点t和时间点(t–k)的观测值的协方差，Var(Xt)是时间序列Xt的方差。偏自相关函数是当前时刻的观测值和滞后k期的相关系数，偏自相关函数通过递归的方式进行，从而得到每个滞后期的偏自相关系数。计算结果如图9所示，由图9（a）和9（b）可知，残差是相互独立的，表明该模型表现良好。

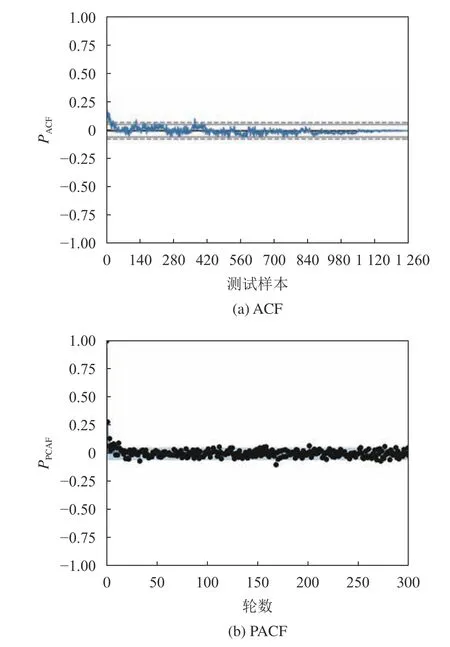
图9 模型性能评价图Fig. 9 Model performance diagram

2.2.3实验结果对比

原始LSTM网络通过非线性激活函数提取数据的非线性特征，并使用存储单元存放用于预测的长期信息。但没有对不同时间序列长度的数据给予不同的关注，故可能丢失重要隐藏状态信息。基于注意力的LSTM模型利用注意力机制以解码器前一次隐藏状态作为参考，为编码器隐藏状态分配不同的关注权重，以达到高精度预测的目的。本文使用的STA–LSTM模型不仅能自适应地发现跨时间序列长度的相关样本，还能自适应地识别与预测指标相关的输入变量。图10为6种算法的预测值和真实值的对比。GRU网络参数相对较少，对于复杂地下水位数据处理难度稍大，图10（a）表明，GRU在极值处存在较为明显的预测失效；Elman网络因其只有一层全连接层而无法充分捕捉数据中的复杂非线性关系，图10（b）表现出预测趋势与真实值接近但预测误差较大，其θRMSE高达0.799 43；传统的LSTM由于注意力不足导致无法充分考虑数据中不同时间点之间的重要性差异，在地下水位突变处尤容易出现预测失误；VA-LSTM重点处理数据的不确定性，对于长期趋势和季节性预测十分受限，面对时间跨度长达十余年的数据，该算法表现较差，其θMAE和θRMSE分别高达1.033 50和1.274 78；S–LSTM未能充分考虑地下水位数据的特殊性从而影响预测性能，预测值相对于真实值普遍偏低；由于STA–LSTM算法中的空间-时间融合注意力机制不仅可快速识别与水位相关联的关键变量还能有效捕捉时间上的依赖关系，实现动态调整权重，故能有效提高水位的预测精度，且算法对复杂水位数据有较好的自适应性和较强的鲁棒性。其θMAE和θRMSE低至0.01166和0.01462。

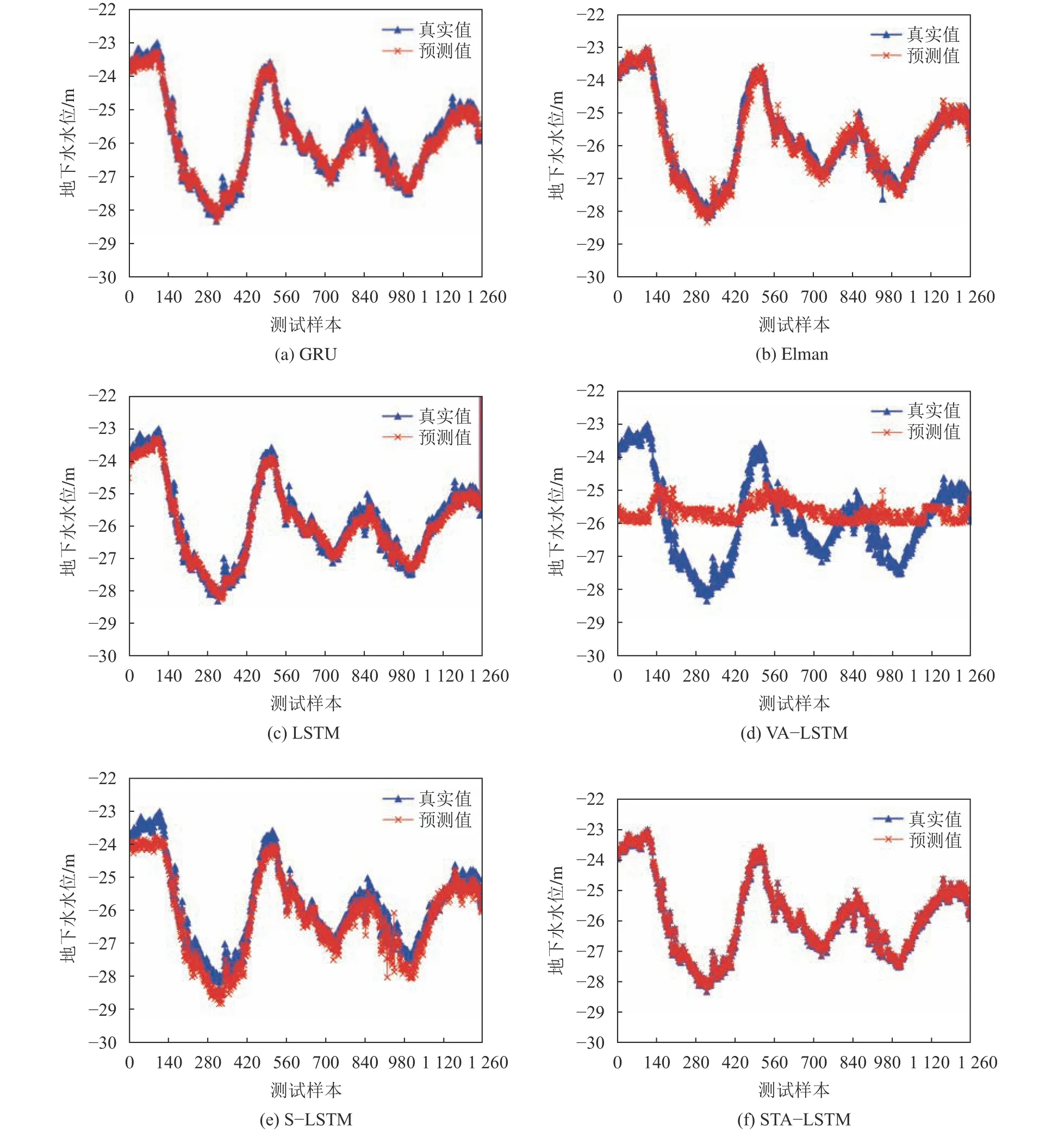
图10 不同算法预测效果对比Fig. 10 Comparison of prediction effects

图11展示了STA–LSTM算法的损失图和残差图，可以看出，STA–LSTM的损失在100轮以前已经降至较低水平，残差较小且都稳定集中分布在0左右。

表1比较了使用测试数据集的6个不同算法的预测性能。从表1可以看出，STA–LSTM算法具有最低的θMAE和θRMSE，以及最高的相关系数，证明其预测误差最小，也证明了该算法在处理复杂、时间跨度大的数据集时展现出的较好的鲁棒性和自适应能力。由图10、表1可知，STA–LSTM弥补了LSTM面对长期历史数据时的注意力低的问题，同时充分考虑地下水位数据中不同时间点之间的重要性差异以及数据的特殊性，显示了本文所提出的算法的优越性与有效性。

图11 STA–LSTM损失图、残差图Fig. 11 STA–LSTM loss diagram and residual diagram

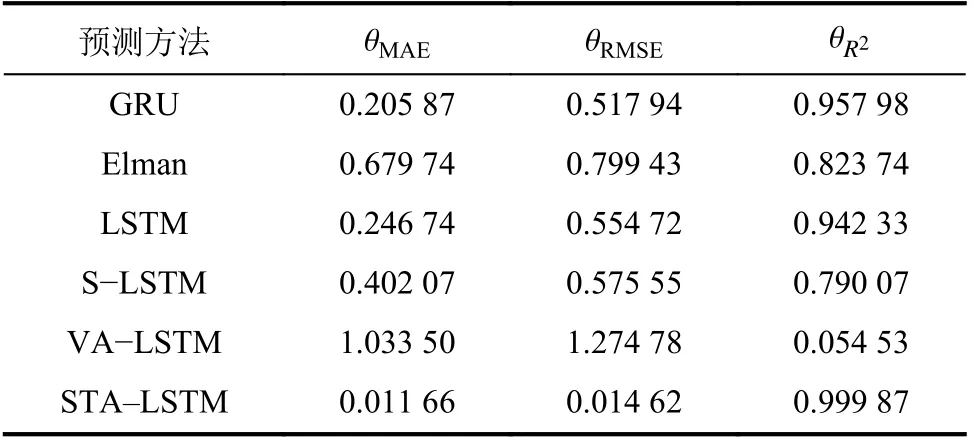
表1 不同预测方法的预测效果Tab.1 Prediction effects of different methods

为体现本文所使用的STA–LSTM算法面对复杂数据时的强适应性，除了使用意大利小镇Petrignano的地下水位数据集验证算法有效性，本文另外使用Powell湖水氧含量数据集和化工领域脱丁烷塔数据集来验证算法的泛化性能。Powell湖水氧含量数据集是通过流入水量、总排出量、湖水pH值、湖水蒸发量、湖水温度、水压等对湖水氧含量进行预测；脱丁烷塔数据集是通过塔顶温度和压力、回流流量、底部温度、流向下一阶段的流量等对丁烷浓度进行预测。表2和图12显示其预测效果仍然保持较好水平，表明本文的算法在面对不同复杂数据时的强适应性和强鲁棒性。

表2 不同数据集的预测效果Tab.2 Prediction effects of other datasets

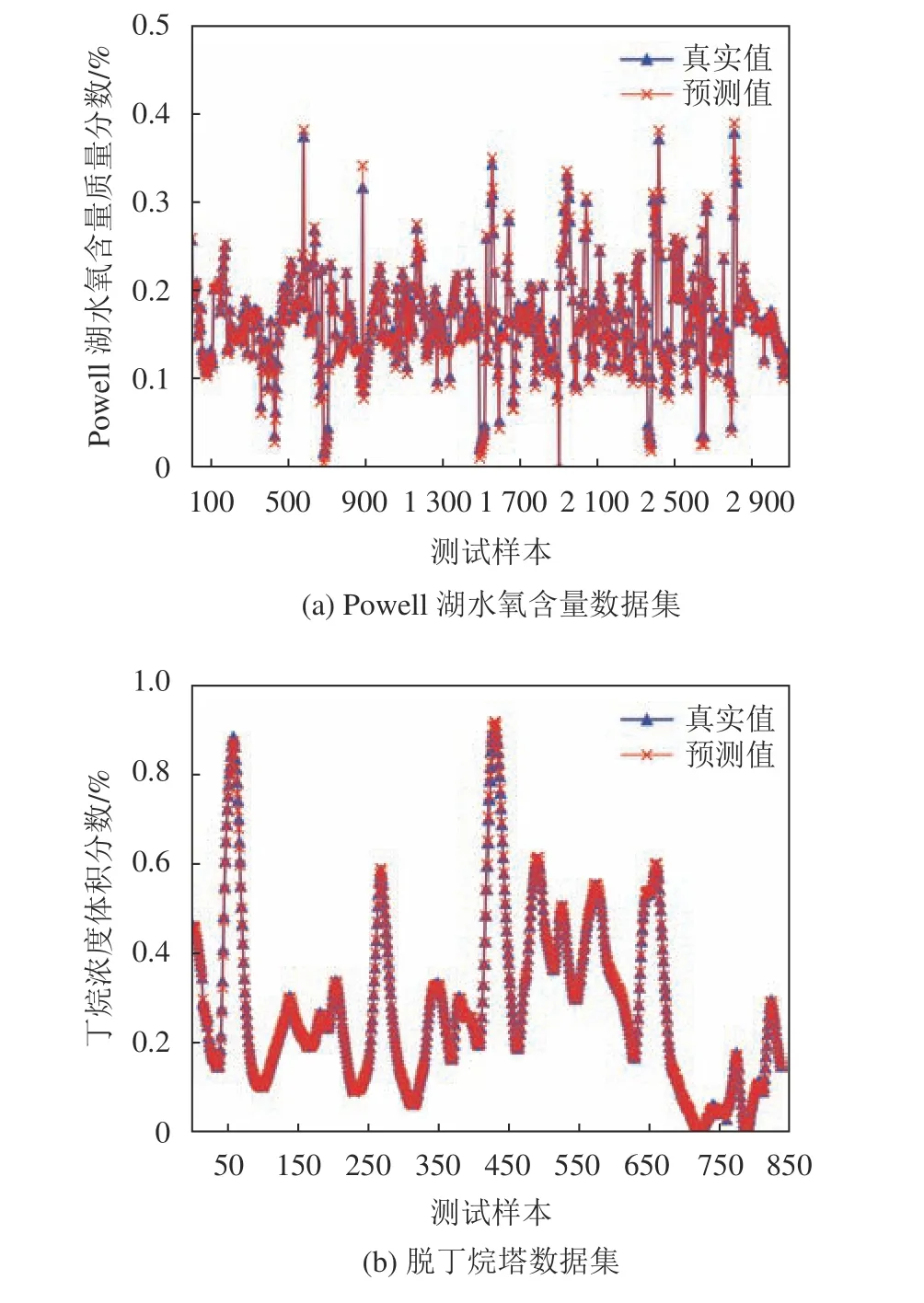
图12 不同数据集预测效果对比Fig. 12 Comparison of prediction effect of other datasets

3 结 论

本文针对水文预测中存在的准确度低、灵敏度低、泛化能力弱等问题，提出了基于融合注意机制LSTM预测模型（STA–LSTM）。融合了时间注意力机制和空间注意力机制的LSTM网络可以动态地调整权重。其中，空间注意力机制可快速识别与水位相关联的关键变量，更准确捕捉影响地下水位的多因素间的依赖模式和关联性；时间注意机制能有效捕捉时间上的依赖关系并自适应地找出不同时间序列长度下与地下水位相关的编码器隐藏状态。本文算法解决了传统算法中数据时空挖掘能力低、处理非线性能力弱、预测结果准确性与鲁棒性等问题，有效补偿了由于数据影响多元带来的数据杂乱和规律复杂造成的预测难度，而且能有效提高水位的预测精度，对复杂水位数据有较好的自适应性和较强的鲁棒性。与对比算法的对比结果表明，提出算法的综合指标优于对比算法，平均绝对误差、均方根误差和相关系数分别为0.011 66、0.014 62、0.999 87。