红外无损检测缺陷尺寸测量方法研究
江海军,马兆庆,王俊虎,张 凯,林 鑫
〈无损检测〉
红外无损检测缺陷尺寸测量方法研究
江海军1,马兆庆2,王俊虎2,张 凯1,林 鑫2
(1. 南京诺威尔光电系统有限公司,江苏 南京 210014;2. 航天材料及工艺研究所,北京 100076)
红外无损检测技术可有效检测金属、非金属、复合材料的内部缺陷,缺陷尺寸是评估缺陷影响的关键参数,本文以半宽高测量算法来实现对缺陷尺寸的半自动测量,首先手动绘制过缺陷中心的直线构成空间像素曲线,采用Savitzky-Golay滤波算法滤波,并自动寻找空间像素曲线半宽高位置,从而实现对缺陷尺寸的测量。通过对塑料试件、碳钢试件、碳纤维复合材料试件研究发现,不同时刻红外图像测量出的缺陷尺寸具有不同的误差,采用清晰时刻红外图像,测量误差在10%内,采用模糊时刻红外图像,测量误差在20%左右,相对于传统手动测量缺陷尺寸,本文方法将有效提高缺陷尺寸测量的精度。
红外无损检测;半宽高测量;缺陷尺寸;缺陷测量
0 引言
红外无损检测技术作为一种非接触式无损检测技术,在航空航天、交通运输、工业制造等领域都有较为广泛的应用[1-5]。红外无损检测技术采用热激励源对试件进行热激励,热激励源包括闪光灯、激光、卤素灯、红外灯、超声激励、涡流激励[6-12]。闪光灯激励作为一种脉冲热激励方式,瞬间产生平面可见光热源加热被测物表面,不仅可以检测导热快的试件,也可以检测极薄的试件,是目前主流的热激励技术之一[13-15]。
缺陷测量是红外无损检测技术一个重要的研究课题,缺陷测量包括测量缺陷深度和缺陷尺寸,缺陷测量受到缺陷深度的影响,随着缺陷深度的变化,缺陷测量误差也会发生变化。缺陷深度测量研究人员比较多,李美华等[16]采用Ansys模拟了二阶微分峰值法的理论,对缺陷深度测量进行了理论研究。曾智等[17]采用二阶微分峰值法对1~6mm平底孔铝试件进行缺陷深度的测量。李晓丽[18]采用二阶微分峰值法对1~6mm不锈钢平底孔与玻璃钢平底孔进行了检测,并与Ansys仿真进行了对比,宽深比满足的情况下,缺陷深度的测量精度为5%左右。缺陷深度测量可以通过二阶微分波峰精准进行定位,缺陷尺寸测量缺少精确定位的算法,目前对缺陷尺寸测量研究比较少,一般通过纯手动标注方式进行测量,手动标注过程很难界定缺陷的边缘,导致纯手动方式易受标注人员客观影响大,造成缺陷尺寸测量误差大。另一个常用的方法是采用半高宽法[19],提取缺陷对应的空间曲线,计算峰值一半对应的位置,从而计算出缺陷尺寸。半高宽法测量时需要选定一帧热图提取缺陷像素曲线,不同帧的热图是否会带来缺陷尺寸测量的误差,目前没有相应的研究。
本文通过半高宽法对不同试件的缺陷尺寸测量进行深度研究,对不同材料、不同深度、不同尺寸的缺陷进行分析,给出半高宽测量法具体测量步骤以及不同帧测量的误差。
1 缺陷宽度测量方法
红外无损检测技术获取的红外热图序列有多帧图像,能看到缺陷的也有多帧图像,不同深度缺陷检测到的时刻不尽相同,目前一般采用的是手动法在热图中直接手动标注,手动法一般是通过绘制直线来确定缺陷的尺寸,手动法标注过程会容易引起缺陷标注带来的人为误差。热图的噪声也会影响半宽高尺寸测量,为了避免人工干扰和噪声的影响,本文采用制冷红外热像仪采集红外热图序列;为了准确寻找过缺陷中心的直线,通过手动方式绘制一条过缺陷中心的直线,采用算法自动查找半高宽,并且会计算手动绘制直线错位一个像素距离上下6条直线的半高宽,共计算7条直线的半高宽,以最大的半高宽作为缺陷尺寸值,以防止手动绘制直线没有通过缺陷中心位置。
1.1 实验系统
采用脉冲红外无损检测技术对试件进行检测,脉冲激励源为闪光灯,系统如图1(a)所示,系统包括3个部分:红外采集系统、闪光灯激励系统、数据处理与控制系统。红外采集系统通过红外热像仪进行数据采集,红外热像仪为FLIR SC7000,属于制冷热像仪,图像分辨率为640×512,全幅帧频为100Hz,最小等效噪声温差<10mK;闪光灯共4个灯管,总能量为12800J,脉冲宽度3ms,闪光灯放置在灯罩内,图1(b)所示,灯罩有效防止闪光灯能量的溢出,使箱内形成均匀光环境,提高加热的效率;数据处理与控制系统,包括参数设置、闪光灯闪光与红外热像仪同步控制、红外热图序列图像处理。

图1 脉冲红外无损检测系统
1.2 半宽高测量
采用半宽高法对缺陷尺寸进行测量,以半宽高为判据方法对试件热图进行测量,从而得到缺陷的尺寸,半宽高法用来计算图像中物体的尺寸,在一定程度上解决了由于图像中边缘模糊导致定位不准的问题。图2是沿缺陷直径方向的温度分布曲线,横坐标为曲线上像素位置,纵坐标为对应直线上像素点的温度值。采用半宽高进行缺陷尺寸测量方法为缺陷边缘位于半宽高的位置1和2,2-1为缺陷的像素尺寸。为单位像素的实际物理距离,则缺陷物理尺寸可以表示为:
=(2-1)×

图2 缺陷像素曲线分布
本文采用的红外热像仪分辨率横向为640pix,对应的物理尺寸为345mm,因此=0.539mm/pix,物理含义是一个像素对应的实际物理尺寸是0.539mm。
1.3 曲线滤波
缺陷像素曲线分布带有噪声信息,如果采用的是非制冷红外热像仪采集的数据,噪声将更加明显,噪声的带入将给计算出来的半宽高带来误差,因此需要采用曲线滤波算法减少噪声带来的影响。Savitzky- Golay曲线滤波算法(SG算法)[20]是Abraham Savitzky和Marcel J. E. Golay提出的基于最小二乘原理的多项式平滑滤波算法,SG算法可有效降低噪声对信号的干扰,大幅提高信号曲线的平滑性。SG算法是一种滑动平均的曲线滤波算法。SG算法滤波效果如图3所示,图3(a)为塑料试件的空间曲线像素值分布,塑料试件温度上升较高,对比范围大的情况下滤波效果不明显,图中有局部放大图,通过局部放大图可以看出滤波效果明显,图3(b)为碳钢试件的空间曲线像素值分布,对比滤波前和滤波后可以看出,空间像素曲线经过SG算法,可以有效提高曲线的平滑度。
1.4 缺陷尺寸测量效果
从热图序列中选取一帧图像,确定缺陷位置,手动绘制一条过缺陷中心的直线,多个缺陷可以绘制多条曲线,图4展示了缺陷尺寸测量效果,图4(a)为手动绘制6条直线,该直线均穿过缺陷的正中心,6个缺陷尺寸均为20mm,缺陷深度从左到右分别为1.0mm、1.5mm、2.0mm、2.5mm、3.0mm、3.5mm。取出每一条空间曲线的像素值分布,再进行曲线滤波,滤波完成后找出最大值和最大值两边的最小值,依据最大值/最小值求出半高宽对应的位置1和2,再把手动绘制曲线缩短1和2,同时显示该缺陷的尺寸信息。选择时间靠后的热图,能看到深缺陷的热图,对于浅缺陷的区域、其清晰度会相对模糊一些,在同一帧热图上进行缺陷测量,从缺陷尺寸测量结果上看,缺陷越深,缺陷尺寸越准确,缺陷越浅,缺陷尺寸误差越大。
2 不同试件缺陷尺寸测量
为了对比材料、深度、缺陷尺寸对缺陷尺寸测量的影响,采用了金属、非金属、复合材料3种不同的材料进行对比研究。金属材料采用的是碳钢,非金属材料采用的是ABS(Acrylonitrile- butadine- styrene)塑料,复合材料采用的是碳纤维复合材料,所有的缺陷都是圆孔缺陷。碳钢和ABS塑料采用相同尺寸、相同缺陷深度,大小为190mm×80mm×6mm的试件,两种试件的缺陷分布如图5所示,主要对直径为20mm、15mm、10mm的3种缺陷尺寸进行测试。碳纤维复合材料试件尺寸为100mm×100mm×5mm,主要对30mm、20mm、15mm三种缺陷尺寸进行测试,缺陷尺寸分布如图6所示。

图3 曲线滤波效果对比

图4 缺陷尺寸测量效果展示

图5 碳钢和塑料缺陷分布
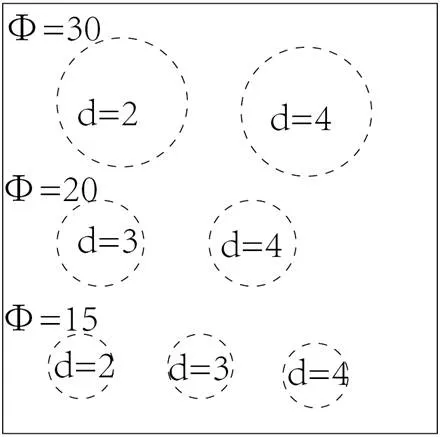
图6 碳纤维复合材料的缺陷分布
2.1 塑料试件
ABS塑料的导热率低,所需采集时间要长一些,因此采集时间设置为70s,采集频率为100Hz,共采集7000帧红外热图序列,选取不同时间的5帧热图,如图7所示,图中可以看出,到采集后期,可以看到全部的缺陷信息。
对于ABS塑料试件,对缺陷直径为20mm、15mm、10mm的不同深度缺陷进行缺陷尺寸的测量。为了更形象地展示缺陷尺寸的测量过程,以直径为20mm、深度为1mm的缺陷为例,取图7所示的7(c)图像,先手动绘制一条过缺陷中心的空间直线,绘制的空间直线需要过缺陷中心,并且直线的起点和终点必须在缺陷之外,确保能按照公式(1)计算出半高宽位置1和2,其余图像都是一样位置的直线。把5帧图像的空间直线对应的温度值绘制成曲线,称为温度-空间曲线,如图8(a)所示,时间越靠前,试件表面的温度越高,时间越靠后,试件的表面温度越低,图7中不同时间的5帧热图的温度-空间曲线呈现从上到下,温度逐渐降低,在热波三维热扩散的过程中,波峰由平顶逐渐变成了抛物线形状,温度-空间曲线为未滤波的原始曲线,计算半高宽时进行SG滤波。按照公式(1)计算每一条曲线的半高宽位置,标示在曲线位置上,计算半宽高位置差,便可以得到缺陷的尺寸。需要说明的是半高宽区域温度上升/下降比较陡峭,相邻两个像素点对应的温度差距比较大,在寻找半高宽位置时取整数,会导致从曲线上看求得的半宽高位置不是最小值和最大值一半的位置,如图8(a)时间为8.0s对应的半高宽2位置。5帧热图测量到的缺陷尺寸如图8(b)所示,不同时刻缺陷尺寸测量值在逐渐减小的。

图7 ABS塑料试件红外热图序列

图8 ABS塑料试件5帧热图测量结果
为了更详细研究时间对缺陷尺寸测量结果的影响,选取了更多不同时间的热图进行缺陷尺寸的测量,同一个缺陷尺寸和缺陷深度对应的手动绘制的直线是一致的,由于缺陷深度的不同,缺陷在热图中出现的时刻是不一样的,因此测量结果的根据缺陷深度的不同,测量时选用的图像起始帧和结束帧不同,本文通过手动方式选取,以该缺陷刚出现时刻为起点,以该缺陷消失为终点,图9(a)~(c)对应的是缺陷尺寸20mm的测量结果,图9(d)~(f)对应的是缺陷尺寸15mm的测量结果,图9(g)~(i)对应的是缺陷尺寸10mm的测量结果。对于1mm深度的缺陷,时间越靠前,缺陷尺寸测量越精确,在缺陷刚出现的时刻测量,测量误差可以在3%以内,10mm的缺陷测量时由于一个像素物理尺寸是0.5mm,所以导致测量时1个像素的错位就会导致较大的误差;时间越靠后,缺陷尺寸测量会越小,缺陷尺寸测量误差会越来越大,到60s附近时刻测量缺陷尺寸时,20mm的测量误差是11%,15mm的测量误差是大于11%,10mm的测量误差是16%。对于2mm深度和3mm深度的缺陷,选用不同帧图像测量出来的尺寸有所不同,有的是时间越靠后,测量结果越小,如图9(b)所示;有的是变化起伏比较大,如图9(i)所示,有的表现是无规律的,如图9(h)所示。从上述测量曲线可以得出以下结论,对于塑料试件,不同帧测量的缺陷尺寸有所不同,浅缺陷的尺寸,时间越靠后,测量误差越大。
2.2 碳钢试件
碳钢的导热率高,采集时间需要短一些,因此采集时间设置为3s,采集频率为100Hz,共采集300帧红外热图序列,选取不同时间的5帧热图,如图10所示,图中可以看出,到采集后期,可以看到全部的缺陷信息。
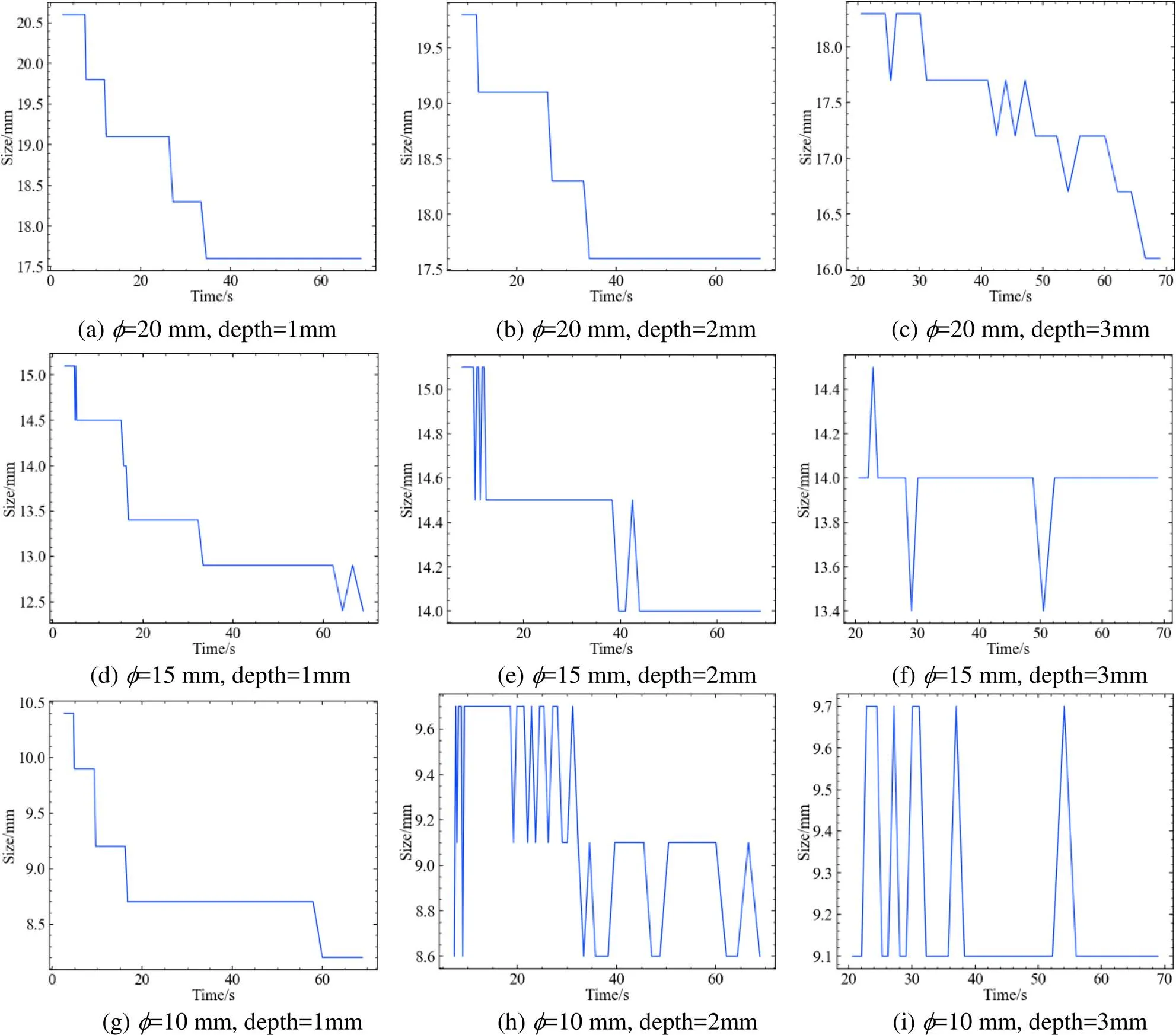
图9 ABS塑料试件不同尺寸/深度缺陷尺寸测量结果

图10 碳钢试件红外热图序列
对于碳钢试件,对缺陷尺寸为20mm、15mm、10mm的不同深度缺陷进行缺陷尺寸的测量,同样以缺陷尺寸20mm、缺陷深度为1mm的缺陷为例进行说明,取图10所示的(c)图像,先手动绘制一条过缺陷中心的空间直线,绘制的空间直线需要过缺陷中心,并且直线的起点和终点必须在缺陷之外,确保能按照公式(1)计算出半高宽位置1和2,其它帧图像计算的缺陷像素分布都是相同位置。把5帧图像的空间直线对应的温度值绘制成温度-空间曲线,如图11(a)所示,与塑料温度-空间曲线相比,碳钢试件表面吸收光脉冲后不仅温升小,而且三维热扩散更快,因此温度-空间曲线纵坐标显示范围只有2.5℃,更大范围地把噪声显示出来,温度-空间曲线表现更大的噪声水平。按照公式(1)计算每一条曲线的半高宽位置,标示在曲线位置上,计算半宽高位置差,便可以得到缺陷的尺寸。5帧热图测量到的缺陷尺寸如图11(b)所示,不同时刻缺陷尺寸测量值在逐渐减小。
图12(a)~(c)是缺陷尺寸20mm的测量结果,图12(d)~(f)是缺陷尺寸15mm的测量结果,图12(g)~(i)是缺陷尺寸10mm的测量结果。相对于ABS塑料试件,碳钢试件缺陷尺寸测量结果跳跃比较快,主要在于碳钢试件表面温升小,表现噪声大,从而计算半高宽时会引入噪声误差,自动计算出来的结果变化大。从上述测量曲线可以得出以下结论,对于碳钢试件,不同帧测量的缺陷尺寸有所不同;采用缺陷刚出现的时刻,缺陷尺寸测量误差会偏小。

图11 碳钢试件5帧热图测量结果

2.3 碳纤维复合材料试件
碳纤维复合材料导热率介于ABS塑料和碳钢之间,采集时间设置为40s,采集频率为100Hz,共采集4000帧红外热图序列,选取不同时间的5帧热图,如图13所示,到采集后期,可以看到全部的缺陷信息。
对于碳纤维复合材料试件,对缺陷尺寸为30mm、20mm、15mm的不同深度缺陷进行缺陷尺寸的测量,以缺陷尺寸30mm、缺陷深度为2mm的缺陷为例进行说明。图13所示的5帧图像的空间直线对应的温度值绘制成温度-空间曲线,如图14(a)所示。5帧热图测量到的缺陷尺寸如图14(b)所示,不同时刻缺陷尺寸测量值在逐渐减小的。
图15(a)~(b)是缺陷尺寸30mm的测量结果,图15(c)~(d)是缺陷尺寸20mm的测量结果,图15(e)~(f)是缺陷尺寸15mm的测量结果。从上述测量曲线可以得出以下结论,对于碳纤维复合材料试件,不同帧测量的缺陷尺寸有所不同,除了=30缺陷深度2mm的缺陷测量结果表现出时间越靠后,测量尺寸越小;其余的测量结果表现出不同时刻测量缺陷尺寸无规律,采用缺陷刚出现的时刻,缺陷尺寸测量误差会偏小。选择清晰化的图像,缺陷尺寸测量将得到更高的精度。

图13 碳纤维复合材料试件红外热图序列

图14 碳纤维复合材料试件5帧热图测量结果
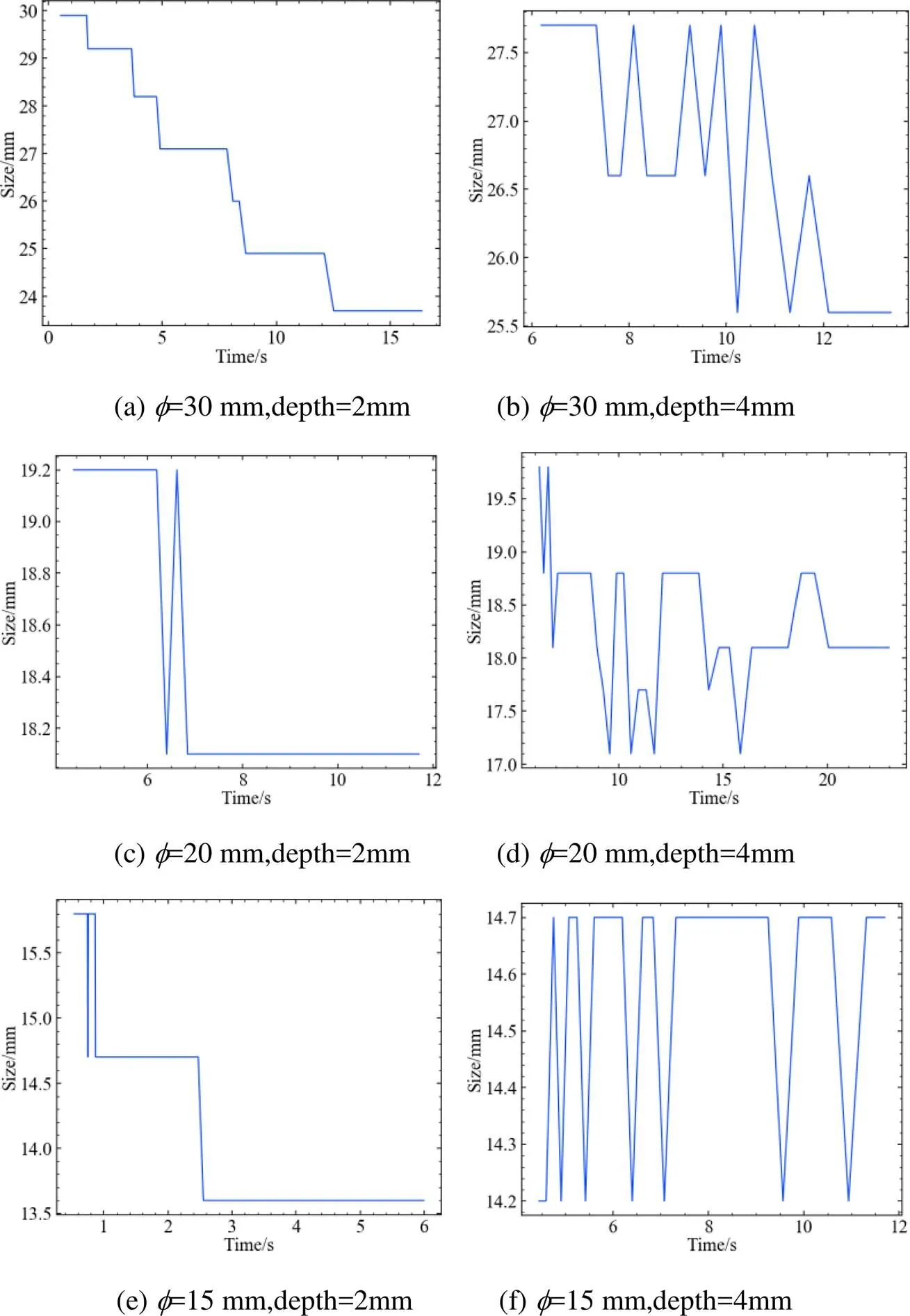
图15 碳纤维复合材料试件不同尺寸/深度缺陷尺寸测量结果
3 缺陷尺寸测量结果分析
本文对不同材质、不同缺陷深度的试件进行缺陷尺寸的测量,采用半宽高测量方法可以实现不同帧缺陷尺寸的自动测量。红外无损检测技术采用主动热激励源对试件进行热激励,并采集热激励后的红外图像序列,在图像采集的过程中,热波(变化的温度场)会进行三维热扩散,热波遇到缺陷时热波会反射到试件表面,试件表面的温度就会产生异常,本文试件采用的都是平底孔缺陷,平底孔缺陷为隔热性缺陷,在红外图像上表象就是缺陷对应的表面位置出现明显的亮斑,亮斑出现的时间和消失的时间与试件材质、缺陷尺寸、缺陷深度都有关系,从而给缺陷的尺寸测量带来偏差。缺陷刚开始出现时,缺陷边缘相对比较清晰,随着热波三维热扩散的进行,缺陷边缘越来越模糊,给缺陷测量带来不利的影响。图16展示了塑料试件、碳钢试件、复合材料试件缺陷尺寸测量最小误差(Min Error)和最大误差(Max Error),最小误差取值处于缺陷显示最清晰的时刻,最小误差取值基本在10%以内;最大误差取值基本上处于缺陷显示最模糊的时刻,最大值误差基本在20%左右。在缺陷测量过程中,采用模糊时刻图像进行缺陷测量,将导致很大的误差,不同缺陷的深度采用同一帧图像进行缺陷尺寸测量,将会导致很大误差,如上文所述图4所示的检测结果。

图16 缺陷尺寸测量误差分析
对于不同深度的缺陷,将采用不同帧的图像进行缺陷测量,如图17所示,缺陷浅的位置,缺陷清晰的时刻在前面帧;缺陷深的位置,缺陷清晰的时刻在后面帧,采用不同帧的图像进行缺陷的尺寸测量,将极大提高缺陷的尺寸测量,对本文的塑料试件、碳钢试件、碳纤维复合材料试件,不同缺陷深度图像,采用不同时刻的图像,再用半宽高自动测量算法,其缺陷尺寸测量误差基本保持在10%以内,测量误差的均值在5%左右,采用该方法将极大提高缺陷尺寸测量的精度。
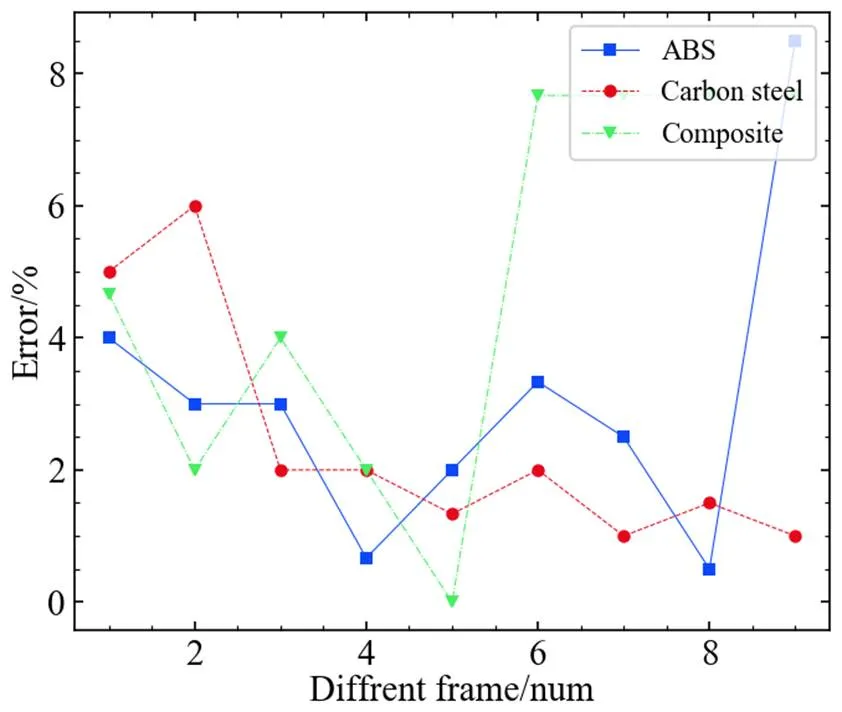
图17 缺陷尺寸测量误差
4 结语
红外无损检测技术的最终目标是检测出试件内部缺陷,并且测量出缺陷尺寸信息,缺陷尺寸信息对于缺陷影响的评估以及缺陷是否可修复具有非常重要的意义。缺陷尺寸一般通过红外图像进行手动测量,手动测量具有很大的误差,且每一次手动测量结果都会不太相同,本文通过手动方式绘制一条过缺陷中心的直线,采用半宽高测量算法自动计算缺陷尺寸,并且会计算手动绘制直线错位一个像素距离上下6条直线的半高宽,共计算7条直线的半高宽,以最大的半高宽作为缺陷尺寸值;为了提高半宽高算法的鲁棒性,采用SG算法对空间像素曲线进行滤波,可以使得空间像素曲线更加平滑。最后通过塑料试件、碳钢试件、碳纤维复合材料试件进行缺陷尺寸测量,采用不同帧红外图像对缺陷尺寸测量,具有不同的测量误差,清晰时刻红外图像误差小,一般小于10%;模糊时刻红外图像误差大,误差在20%,在清晰时刻采用红外图像对3种不同材质、不同深度、不同尺寸的缺陷进行测量,测量误差基本在10%以内,测量误差的均值在5%左右,本文的研究对于脉冲红外无损检测缺陷尺寸测量具有重要的作用和应用价值,下一步研究将自动实现不同缺陷区域清晰时刻的判断,进一步从不同帧图像中提取更加精准的缺陷尺寸。
[1] 刘颖韬, 郭广平, 杨党纲, 等. 脉冲热像法在航空复合材料构件无损检测中应用[J]. 航空材料学报, 2012, 32(1): 72-77. LIU Y T, GUO G P, YANG D G. Pulsed thermography of composite components used in aerospace applications[J]., 2012, 32(1): 72-77.
[2] Khodayar F, Sojasi S, Maldague X. Infrared thermography and NDT: 2050 horizon[J]., 2016, 13(2): 22-25.
[3] 郑凯, 江海军, 陈力. 红外热波无损检测技术的研究现状与进展[J]. 红外技术, 2018, 40(5): 401-411. ZHENG K, JIANG H J, CHEN L. Infrared thermography NDT and its development[J]., 2018, 40(5): 401-411.
[4] 郭伟, 董丽虹, 徐滨士, 等. 主动红外热像无损检测技术的研究现状与进展[J]. 无损检测, 2016, 38(4): 58-66. GUO W, DONG L H, XU B S, et al. Research status and progress of active infrared thermographic nondestructive testing[J]., 2016, 38(4): 58-66.
[5] 刘颖韬, 郭广平, 曾智, 等. 红外热像无损检测技术的发展历程、现状和趋势[J]. 无损检测, 2017, 39(8): 63-70. LIU Y T, GUO G P, ZENG Z, et al. The development history, status and trends of infrared thermographic nondestructive testing[J]., 2017, 39(8): 63-70.
[6] WANG Q, HU Q P, QIU J X, et al. Using differential spread laser infrared thermography to detect delamination and impact damage in CFRP[J]., 2020, 106: 103282.
[7] BU C W, LIU G Z, ZHANG X B, et al. Debonding defects detection of FMLs based on long pulsed infrared thermography technique[J]., 2020, 104: 103074.
[8] Moskovchenko A I, Vavilov V P, Chulkov A O. Comparing the efficiency of defect depth characterization algorithms in the inspection of CFRP by using one-sided pulsed thermal NDT[J]., 2020, 107: 103289.
[9] WANG Hongjin, WANG Nichen, HE Zhiyi, et al. Phase-locked restored pseudo heat flux thermography for detecting delamination inside carbon fiber reinforced composites[J]., 2019, 15(5): 2938-2946.
[10] WANG F, WANG Y H, PENG W, et al. Independent component analysis enhanced pulse thermography for high silicon oxygen phenolic resin (HSOPR) sheet with subsurface defects [J]., 2018, 92: 345-349.
[11] PAN M C, HE Y Z, TIAN G Y, et al. Defect characterization using pulsed eddy current thermography under transmission mode and NDT applications [J]., 2012, 52: 28-36.
[12] FEUILLET V, IBOS L, FOIS M, et al. Defect detection and characterization in composite materials using square pulse thermography coupled with singular value decomposition analysis and thermal quadrupole modeling [J]., 2012, 51: 58-67.
[13] WANG Qiang, HU Qiuping, QIU Jinxing, et al. Using differ-ential spread laser infrared thermography to detect delami-nation and impact damage in CFRP[J]., 2020, 10(6): 1-10.
[14] LEI L, Ferrarini G, Bortolin A, et al. Thermography iscool: defect detection using liquid nitrogen as a stimulus[J]., 2019, 10(2): 137-143.
[15] LIU Y, WU J Y, LIU K X, et al. Independent component thermography for non-destructive testing of defects in polymer composites[J]., 2019, 30(4): 44-49.
[16] 李美华, 曾智, 沈京玲, 等. 脉冲红外无损检测缺陷深度定量测量的数值模拟[J]. 红外与激光工程, 2013, 42(4): 875-879.LI M H, ZENG Z, SHEN J L, et al. Numerical simulation of defects depth quantitative measurement in pulsed infrared nondestructive testing[J]., 2013, 42(4): 875-879.
[17] ZENG Zhi. Depth prediction of non-air interface defect using pulsed thermography[J]., 2012, 48(6): 39-45.
[18] 李晓丽. 红外热波定量测量技术研究及其应用[D]. 北京: 北京理工大学, 2018. LI X L. Studies for Quantitatively Measuring Technique by Using Thermal Wave Imaging and Their Applications[D]. Beijing: Beijing Institute of Technology, 2018.
[19] 黄新萍. 基于脉冲红外热像法的缺陷尺寸测量及有限元模拟分析[D]. 北京: 首都师范大学, 2014. HUANG X P. The Study of Finite-Element Modeling of Defect Size Measuring for Pulsed Thermography Measurement[D]. Beijing: Capital Normal University, 2014.
[20] Nodes T A, Galla gher N C J. Median filters: some modifications and their properties[J], 1982, 30(5): 739-746, Doi: 10.1109/TASSP.1982.1163951.
Research on Defect Size Measurement Methods for Infrared Thermography
JIANG Haijun1,MA Zhaoqing2,WANG Junhu2,ZHANG Kai1,LIN Xin2
(1. Novelteq Ltd., Nanjing 210014, China;2. Aerospace Research Institute of Materials and Processing Technology, Beijing 100076, China)
Infrared thermography effectively detects internal defects in metals, non-metals, and composite materials. Defect size is a key parameter for evaluating the impact of defects. We used a half width height measurement algorithm to achieve semi-automatic measurement of defect size, manually drawing a straight line through the center of the defect to form a spatial pixel curve, and used the SG filtering algorithm to filter, automatically finding the half width height position of the spatial pixel curve, thus achieving defect size measurement. Through research on ABS plastic, carbon steel, and carbon fiber composite material specimens, it was found that the defect sizes measured by infrared images at different times have different errors. Using clear infrared images at different times, the measurement error was within 10%, whereas using fuzzy infrared images at different times, the measurement error was approximately 20%. This will effectively improve the accuracy of defect size measurements.
infrared thermography, half width height measurement, defect size, defect measurement
TN219
A
1001-8891(2024)01-0107-10
2023-09-19;
2023-11-03.
江海军(1988-),男,硕士,研究方向为红外无损检测技术及图像处理。E-mail:hjiang@novelteq.com。

