考虑绿灯末期非机动车通行安全的四相位交叉口信号配时优化

唐 轶,朱从坤

(苏州科技大学,江苏 苏州 215011)

0 引 言

作为道路弱势者,非机动车在道路行驶过程当中更容易受到伤害。据统计,2020年非机动车交通事故发生数为29 969起,死亡人数为4 373人[1],2021年交通事故数量上升到35 141起,其中死亡人数更是达到了4 525人[2],在这之中交叉口是事故高发地。因此如何解决交叉口非机动车通行安全问题已经成为了迫在眉睫的事情。

白辂韬等[3]提出一种基于机动车、非机动车、行人同时考虑道路、环境等方面因素的交通管理控制模型,将机非混行交叉口的通行效益最大化。邢冰等[4]考虑非机动车对机动车的阻滞性,以区域内机动车总延误为优化目标,折减交叉口通行能力,提出相邻交叉口的相位差优化模型。韩印等[5]优化了相邻交叉口的相位差。以机动车的总延误为优化指标,建立基于非机动车影响下的交通控制优化模型。李强[6]以饱和度为约束,选取机动车、非机动车、行人三者的延误时间加上机动车停车次数、交叉口通行能力5个指标作为优化指标,确定权重系数,运用遗传算法对多目标优化模型进行求解。

综上,目前对非机动车信号配时优化设计的研究大多集中在混合交通流的通行效率方面,将非机动车安全因素考虑进信号配时设计却很少涉及。因此以重点解决绿灯末期非机动车通行安全为目标,对四相位信号交叉口信号配时进行优化设计,其研究成果对交叉口非机动车的交通安全管理具有重要的价值。

1 绿灯间隔时间优化

绿灯间隔时间的定义为即将失去通行权的相位绿灯结束到得到通行权的相位绿灯开始之间的间隔。绿灯间隔时间的长短直接关系到信号交叉口的事故率。当绿灯间隔时间的长短不合理时,将会对信号交叉口的车辆通行安全造成很大的威胁。所以,在设计绿灯间隔时间时,必须将相邻两相位的停车线至可能发生交通冲突的点之间的行驶时间差完全考虑在内[7]。

在以往的研究中绿灯间隔时间的设计仅仅考虑了机动车的通行安全,对非机动车的通行安全涉及很少。因此为了确保本相位绿灯即将截止时通过交叉口的非机动车不会与下一相位绿灯刚启亮时驶出的机动车发生冲突,四相位信号交叉口绿灯间隔时间的确定方法如下。

根据目前的交通规则,黄灯启亮后,如果车辆已经越过停止线将仍然可以继续通行。因此,冲突的相交过程应符合以下条件:

t优i=tbf+tfi-tS-thi

(1)

式中:t优i为优化后i相位绿灯间隔时间,s;tbf为交叉口正常行驶的非机动车辆的制动时间,s,一般情可取 2.0 s;tfi(ffi=Sfi/Vfi,Sfi为i相位末期非机动车辆从停车线到冲突点的距离,m,Vfi为行驶速度,m/s)为i相位末期非机动车车辆由停止线行驶至冲突点的时间,s;tS为机动车辆启动和反应所需的时间,s,一般可取1.8～2.0 s(与车型有关,当大型车占比较大时,需要另外计算);thi为i相位的下一相位机动车车辆从停止线行驶到冲突点并且停车所用的时间,s。

这时相交车流的任意一方运行状态将发生改变,也就是要强制减速和停车,以避免发生交通碰撞。

当交叉口行人流量较大,且没有设置行人专用相位,但是斑马线上设置了行人过街安全岛,在这种情况下,大多数行人在绿灯末期会选择进入交叉口,在安全岛上等待下一个绿灯相位。为了避免下一个相位机动车和非机动车与行人之间的冲突,绿灯时间间隔优化为

(2)

式中:abi为i相位过街人行横道的长度,m。vp为行人过街平均速度,m/s。

这里公式(2)有两个假设,假设一:本相位绿灯刚结束时,行人刚好进入交叉口,此为最不利条件;假设二:行人到达人行横道安全岛后,便停止过街,等候下一个绿灯相位。

绿灯间隔时间的设计存在着一个最低值,在国外,最低值通常为4 s,而且在进行信号控制器的设计和制作时,都会用内部的电路编程来固定这一最低限值,无论在什么情况下,信号控制器都会确保两个相位之间的绿灯间隔时间不小于4 s。

2 非机动车绿灯提前截止

当交叉口较大,或者交叉口单方向较长,按照以上优化方案可能会导致绿灯间隔时间过长,信号周期总损失时间过大,造成总周期过长,增加交叉口车辆的延误。此时为了保障非机动车的行驶安全,可以使用非机动车绿灯提前截止的方法。交叉口非机动车绿灯提前截止计算如公式(3)所示。

Tji=tbf+tfi-tS-thi-ti

(3)

式中:Tji为i相位非机动车提前截止时间,s;ti为i相位原绿灯间隔时间,s。

绿灯提前截止虽然可以有效地减少非机动车与下一相位的机动车交叉冲突,但是由于通行时间的缩短,非机动车的通行效率并不能得到良好的保障。因此需要根据交叉口的实际条件和不同相位的实际需求选择不同的优化方案,在同一个交叉口也以选择将两种方案相结合的方式可以达到一种很好的优化效果。

3 机非冲突影响下的非机动车最小绿灯时间确定

最小绿灯时间指为了保证车辆通行安全,在一个信号周期内取得通行权相位的车辆最小绿灯通行时间。为保障非机动车交叉口通行安全,非机动车通行最小绿灯时间确定如下。

3.1 左转非机动车最小绿灯时间

当机动车与非机动车发生交通冲突时,通常都会有一方选择避让以避免造成交通事故。在调查研究中发现,机动车与非机动车发生交通冲突时,会出现两种情况,机动车避让非机动车和非机动车避让非机动车。在某个周期时间内,将非机动车避让次数与机非冲突总数的比值定义为非机动车避让率,计算如公式(4)、公式(5)所示。

(4)

(5)

式中:Km为机动车避让率;Kn为非机动车避让率;Cmn为机动车避让非机动车的次数;Cnm为非机动车避让机动车的次数;C为机非冲突总次数。

建立线性回归模型,对非机动车避让率与机动车流量和非机动车流量之间的关系进行研究。建立非机动车避让率与机动车流量和非机动车流量之间的关系模型如公式(6)。

Kn=a·Qm+b·Qn1+c·Qn2+d

(6)

式中:Qm为机动车流量;Qn1为自行车车流量;Qn2为电动自行车流量;a,b,c,d为模型系数。

通过现场交通调查数据,对非机动车避让率与机动车和非机动车流量之间的关系进行线性回归分析,得出判定系数R2为0.836,说明该线性回归模型拟合度较好,模型的可行性良好。模型系数a,b,c,d分别为5.62×10-4、9.56×10-5、7.62×10-5、0.79。得出非机动车避让率和机动车和非机动车流量的关系模型如公式(7)所示。

Kn=5.62×10-4·Qm+9.56×10-5·Qn1+7.62×10-5·Qn2+0.79

(7)

当机非发生交通冲突时,避让的一方每次避让将会造成一定的时间损失。电动自行车由于启动速度较快每次避让的损失时间相比于普通自行车来说较短,这里考虑最不利因素即非机动车每次避让的损失时间按普通自行车每次避让的损失时间取值为1～2 s,这里取平均值1.5 s。

非机动车一次左转过街最小绿灯时间确定如公式(8)所示。

(8)

式中:gif左min为i相位左转非机动车最小绿灯时间,s;N左为左转非机动车与机动车冲突次数;T清为非机动车的清空时间,s,一般可取5 s;S左为非机动车左转过街长度,m;v左为非机动车左转过街平均速度,m/s;t优i为优化后i相位绿灯时间间隔时长,s。

这里设置的非机动车清空时间是考虑让上一周期停车等待绿灯的非机动车全部开始通过交叉口。

3.2 直行非机动车最小绿灯时间

根据上一节提出的考虑机非冲突造成的时间损失,直行非机动车最小绿灯时间确定如公式(9)。

(9)

式中:gi直min为i相位直行非机动车最小绿灯时间,s;N直为直行非机动车与机动车冲突次数;S直为非机动车直行过街长度,m;v直为非机动车直行过街平均速度,m/s;t优i为优化后i相位绿灯时间间隔,s。

但是交叉口直行最小绿灯时间同时要满足行人的最小过街需求。为了让行人安全通过交叉口,需要确定行人过街所需要的最小时间。行人过街最小绿灯长[8]如公式(10)所示。

(10)

式中:gi人min为i相位行人过街最小绿灯时间,s;D为行人的滞后时间,s;lp为行人过街长度,m;vp为行人过街平均速度,m/s;t优i为优化后i相位绿灯时间间隔,s。

这里设置的行人滞后时间是考虑让上一周期停止等待绿灯的行人全部开始通过交叉口。D的取值一般为7 s。因此最终直行非机动车最小绿灯时间取两者的最大值如公式(11)所示。

gif直min=max{gi直min,gi人min}

(11)

式中:gif直min为最终i相位直行非机动车最小绿灯时间,s。

在实际交通信号配时当中,都要确保每个相位有不低于15 s的绿灯时间,如果时间过短会造成车辆启动频繁,从而增加车辆延误,降低通行效率。

4 实例分析

为了检验方法在实践中的可行性,选取苏州市核心地带非机动车交通流量较大的典型四相位信号交叉口桐泾北路和金门路交叉口作为案例进行实证分析。

4.1 信号配时优化

(1)流量比计算。

使用HCM2000的估算方法来计算饱和流量,以信号交叉口各车道或车道组的饱和流量为基础,用车道或车道组的通饱和流量乘以各种影响因素的折算系数对饱和流量进行折减。

饱和流量的修正如公式(12)和公式(13)所示。

S修=SO·M·f总

(12)

式中:S修为修正后车道饱和流量;SO为车道或车道组的基本饱和流量;M为车道组的车道数;f总为综合校正系数。

f总=fH·fG·fL·fR·fW

(13)

式中:fH为重型校正系数;fG为坡度校正系数;fL为左转校正系数;fR为右转校正系数;fW为车道宽度校正系数。

左转车道、直行车道、右转车道的基本饱和流量分别取1 800、1 800、1 550 pcu/h。其中电动自行车换算成标准自行车的换算系数取1.3[9],将非机动车流折算成机动车流,换算系数为0.24[10]。交叉口各进口道车流量和冲突数据如表1所示,流量比计算如表2所示。

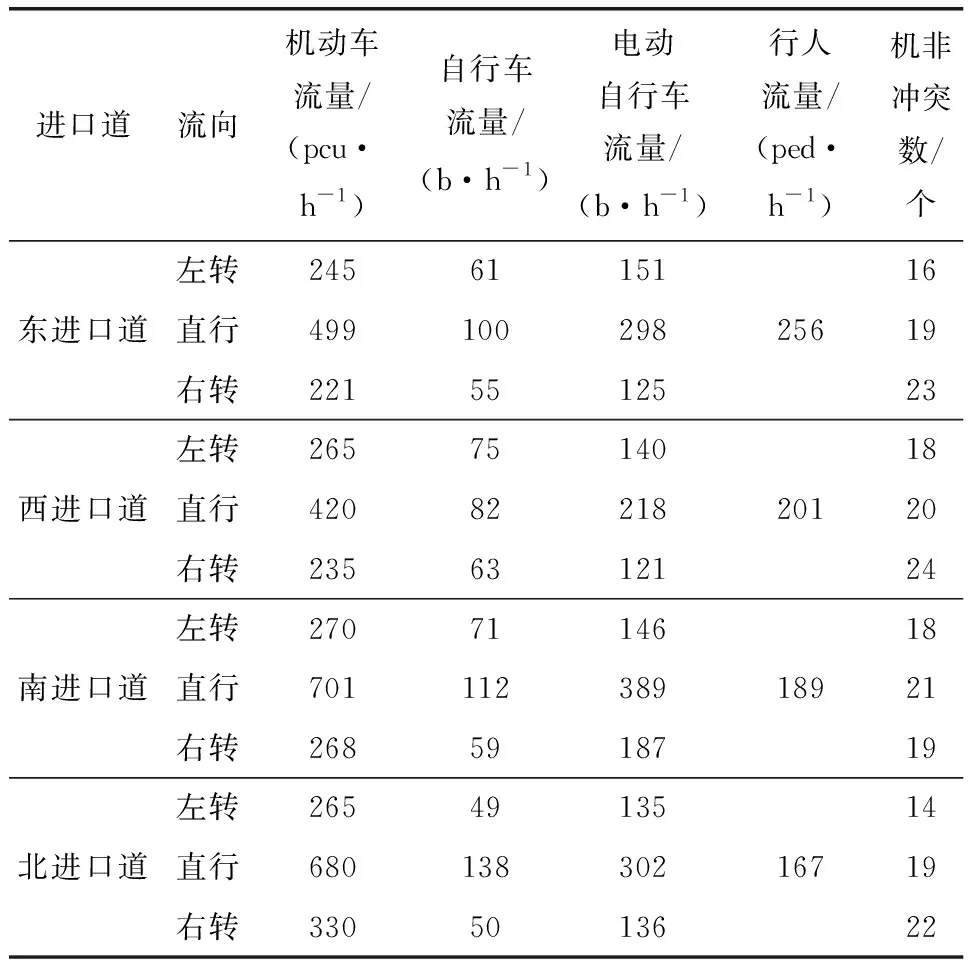
表1 交叉口各进口道高峰小时交通流量和冲突数

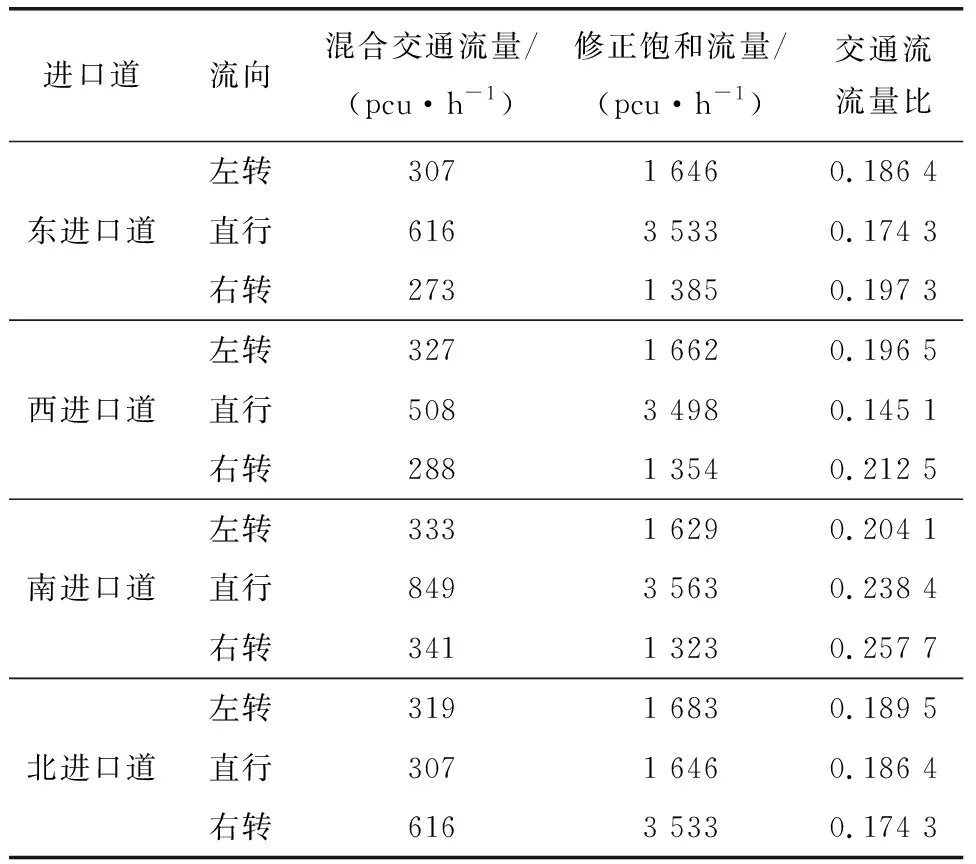
表2 交叉口各进口道高峰小时流量比统计表

则各相位的交通流流量比如下所示。

相位一(东西向直行)的流量比:y1=max(0.174 3,0.145 1)=0.174 3;

相位二(东西向左转)的流量比:y2=max(0.186 4,0.196 5)=0.196 5;

相位三(南北向直行)的流量比:y3=max(0.238 4,0.226 3)=0.238 4;

相位四(南北向左转)的流量比:y4=max(0.204 1,0.189 5)=0.204 1;

交叉口综合流量比:Y=0.813 3<0.9。

(2)绿灯间隔时间的求解。

根据优化方案每一相位绿灯间隔时间计算结果如下。

由此可以看出,第二相位和第四相位需要的绿灯间隔时间较大,信号周期偏大,因此第二相位和第四相位采用非机动车绿灯提前截止的方法保证绿灯末期非机动车的通行安全。

新的每一相位的绿灯间隔时间如表3所示。

表3 考虑非机动车绿灯提前截止的不同相位绿灯间隔时间

根据非机动车绿灯提前截止优化方案,第二相位和第四相位的非机动车绿灯提前截止时间计算得:

Tj2=tbf+tf2-ts-th2-t2=9-5=4 s,

Tj4=tbf+tf4-ts-th4-t4=8-5=3 s。

周期总损失时间为

L=∑(l+ti-A)=(3+5-3)×4=20 s。

(3)最小绿灯时间。

左转非机动车最小绿灯时间计算得:

直行最小绿灯时间计算得:

g1f直min=max{25,15}=25s,

g3f直min=max{24,14}=24 s。

所以东西向直行最小绿灯时间为25 s,南北向直行最小绿灯时间为24 s。东西向左转最小绿灯时间为17 s,南北向左转最小绿灯时间为19 s。

(4)最佳周期时长。

(5)有效绿灯时间。

GE=T-L=187-20=167 s。

交叉口各相位的有效绿灯时间计算得:

g2=40 s,g3=49 s,g4=42 s。

考虑到最小绿灯时间,则有效绿灯时间为:

ge1=max{g1fmin,g1}=36 s,

ge2=40 s,ge2=49 s,ge2=42 s。

每一相位的实际显示绿灯时间为:

G1=ge1-A+l=36 s,G2=40 s,G3=49 s,

G4=42 s。

因此优化配时方案为第一相位(东西向直行)绿灯36 s,黄灯3 s,全红时间2 s;第二相位(东西向左转)绿灯40 s,黄灯3 s,全红2 s,非机动车绿灯提前截止4 s;第三相位(南北向直行)绿灯49 s,黄灯3 s,全红2 s;第四相位(南北向左转)绿灯42 s,黄灯3 s,全红2 s,非机动车绿灯提前截止3 s。信号周期时长为187 s。

4.2 VISSIM仿真与效果分析

当机非发生冲突时,机动车和非机动车的延误必然增加,当延误增加时,非机动车强行穿越机动车或机动车强行穿越非机动车的可能性都会增加,机非冲突也会有所增加,造成非机动车的行车安全性下降。可以得出机动车和非机动车的车均延误间接反映了交叉口的机非冲突数。因此采用机动车和非机动车的车均延误作为评价指标对优化前后非机动车的安全性进行对比分析。

通过VISSIM软件对交叉口信号配时优化后的方案与原交叉口交通控制方案进行仿真对比分析,优化前后的机动车和非机动车平均延误如表4、表5所示。

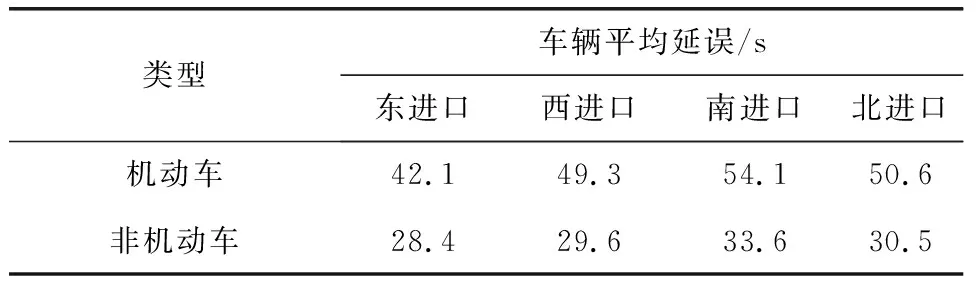
表4 信号配时优化前车辆平均延误

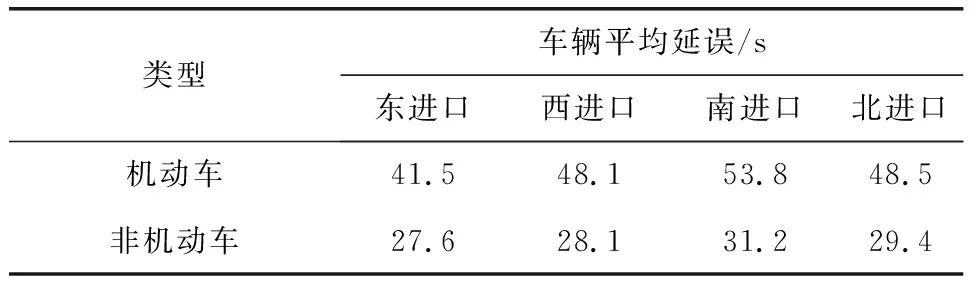
表5 信号配时优化后车辆平均延误

根据表4和5可知,其中机动车东进口道平均延误时间降低了1.4%,西进口道降低了2.4%,南进口道降低了0.6%,北进口道降低了4.2%。非机动车东进口道降低了2.8%,西进口道降低了5.1%,南进口道降低了7.1%,北进口道降低了3.6%。可以看出机动车延误和非机动车不同进口道均有少量降低。由于信号配时优化方案重点解决绿灯末期通行的非机动车与下一相位机动车之间的冲突,而这一部分的冲突占比较少,因此优化后延误降低较少,符合文章优化需求,验证了优化方案的可行性。

5 结 论

以绿灯末期非机动车的通行安全为优化目标,以改进的韦伯斯特信号配时方法为基础,对绿灯间隔时间、非机动车最小绿灯时间、饱和流量等参数进行优化。同时构建了与绿灯间隔时间相协调的非机动车绿灯提前截止配时方案。用VISSIM仿真软件对优化后的信号配时方案进行效果评价,结果表明,交叉口机动车平均延误降低了2.2%,非机动车平均延误降低了4.7%,间接表明绿灯末期机非冲突有所降低,绿灯末期的非机动车行驶安全得到良好保障。该研究成果对解决交叉口绿灯末期非机动车的通行安全具有重要意义,同时也为城市道路交叉口非机动车的交通管理与设计规划提供理论依据。