316L不锈钢非比例循环硬化特性的数值模拟

金 丹,郭超越,孙梦莹,刘 壮,李卓群

(沈阳化工大学 机械与动力工程学院,沈阳 110142)

0 引 言

316L不锈钢因其良好的力学性能和耐腐蚀性能而被广泛用在核电站中的热交换器、主容器和第四代核反应堆等设备中[1],其工作条件比较恶劣,通常承受复杂的多轴载荷作用,因此研究该材料的多轴疲劳特性具有重要意义。

目前,采用本构关系探讨复杂载荷条件下应力-应变特性已成为各国学者关注的课题。自从ARMSTRONG和FREDERICK[2]在线性随动硬化模型中引入动态恢复项,提出著名的A-F模型以来,学者们在将背应力分为多个分量、动态恢复项中引入门槛值以及模型叠加等方面均做了大量的工作[3-6]。ABDEL-KARIM等[6]将A-F和O-WI模型叠加,得到了AF-OW模型,实现了对多轴棘轮效应的准确模拟。将随动硬化模型与各向同性硬化准则结合可描述疲劳过程中的循环硬化或循环软化现象[7-12]。SAAD等[9]在各向同性硬化准则中耦合线性项,并结合Chaboche随动硬化模型对P91钢的循环软化特性进行了较准确的模拟。ZHOU等[10]采用上述方法实现了对316L不锈钢初始循环硬化而后循环软化现象的描述。XIE等[11]分别在Chaboche随动硬化模型和各向同性硬化准则中引入记忆平面相关的描述,准确地模拟了316L不锈钢循环硬化行为的幅值相关性。曹宇等[12]基于Chaboche理论,发展了一个能够描述材料蠕变和循环特性的本构模型,对P92钢在复杂载荷下的蠕变-疲劳曲线进行了较准确的模拟。

综上,随动硬化模型与各向同性硬化准则相结合能够较好地描述材料的循环特性,但是仅限于单轴路径和比例路径等简单路径,而在描述非比例路径下的循环特性,尤其是用于描述附加强化较强的材料时,模拟结果误差较大[13]。因此,对现有模型进行修正来实现对非比例路径下循环特性的准确模拟是很有必要的。基于此,作者对316L不锈钢在比例和非比例应变路径下的循环特性进行分析,以可描述复杂载荷路径下应力-应变关系的AF-OW模型为基础,结合各向同性硬化准则对各加载路径下的循环特性进行模拟;基于材料在非比例应变路径下所表现出来的附加强化效应,将非比例度的概念嵌入到各向同性硬化准则中,对非比例路径下的循环特性进行模拟,并进行试验验证。研究结果可为316L不锈钢相关构件的结构设计提供参考。

1 试样制备与试验方法

试验材料为316L奥氏体不锈钢,其化学成分(质量分数/%)为0.12C,0.31Si,1.65Mn,12Ni,16.87Cr,2.05Mo,0.037P,0.012S;室温下的弹性模量为200 GPa,泊松比为0.3,屈服强度和抗拉强度分别为247 MPa和564 MPa。在经过1 080 ℃保温后进行水冷处理的试验钢上截取薄壁圆管试样[14]。试样中心标距段长度为12 mm,内、外直径分别为9 mm和12 mm,具体尺寸及形状见图1。

图1 薄壁圆管试样的形状和尺寸Fig.1 Shape and dimension of thin-walled round tube specimens

采用多轴液压疲劳试验机进行室温应变控制拉-扭疲劳试验[14],选择等效应变范围为0.7%,等效应变速率为1×10-3s-1,采用对称三角波控制,加载应变路径为单轴路径、比例路径、十字路径和圆路径,具体路径如图2所示。

图2 不同应变路径示意Fig.2 Schematic of different strain paths: (a) uniaxial path; (b) proportional path; (c) cruciform path and (d) circular path

2 试验结果与讨论

由图3可以看到,不同应变路径下316L不锈钢在循环初期均表现出不同程度的循环硬化,等效峰值应力在循环次数为30周次左右达到饱和,随后进入循环稳定阶段。采用硬化率RH表达材料循环硬化程度[15],其表达式为

图3 不同应变路径下等效峰值应力与循环 次数的关系Fig.3 Relation between equivalent peak stress and cycle number under different strain paths

RH=σmax/σmax(1)-1

(1)

式中:σmax为最大等效峰值应力;σmax(1)为第1周次的等效峰值应力。

在单轴和比例路径下,计算得到的硬化率分别为5.2%和4.5%,而十字和圆路径下的硬化率分别为38.2%和44.6%。十字路径和圆路径为非比例应变路径,可见在非比例应变路径下,316L不锈钢产生了明显的附加强化。

3 本构模型的建立与试验验证

3.1 模型的建立

循环塑性本构模型包括应变分解、流动准则、随动硬化律和各向同性硬化律[16]。对于小变形问题,总应变可分为弹性应变和塑性应变:

ε=εe+εp

(2)

εe=C…σ

(3)

式中:εe为弹性应变;εp为塑性应变;σ为应力张量;C为四阶刚度张量。

材料的应力状态服从Von Mises准则:

(4)

式中:s,a分别为偏应力和偏背应力张量;σy为屈服应力。

塑性部分采用塑性流动准则表示,如下:

(5)

(6)

随动硬化律采用AF-OW随动硬化模型[6],具体公式为

(7)

ai=

(8)

假定材料的循环硬化主要来自各向同性强化,即屈服面的扩展,采用Chaboche提出的非线性各向同性硬化准则(Chaboche准则)[7]描述,具体表达式为

σy=σy0+R

(9)

R=Q[1-exp(-bp)]

(10)

式中:σy0为材料的初始屈服应力;R为各向同性硬化增量;Q和b为材料参数;p为累积塑性应变。

316L不锈钢在非比例路径下产生了明显的附加强化,因此将非比例度的概念嵌入到非线性各向同性硬化准则中[17]。将屈服面半径分为比例和非比例载荷屈服面半径两部分,即

R=R1+R2=Q1[1-exp(-b1p)]+

Q2[1-exp(-b2p)]

(11)

Q2=QAS(A){1-exp[D(A)p]}

(12)

D(A)=(d-f)A+f

(13)

QAS(A)=AQ∞+Q0

(14)

A=1-cos2θ

(15)

(16)

3.2 参数的确定

根据单轴拉伸曲线确定随动硬化参数ci和ri[16],依据不同条件下试验得到的峰值应力和累积塑性应变,利用式(9)～式(14)确定各向同性硬化相关参数,其中累积塑性应变p由2ΔεpNf(Δεp为半寿命塑性应变范围,Nf为疲劳寿命)计算得到。得到的参数值见表1。

表1 材料参数Table 1 Material parameters

3.3 试验验证

3.3.1 比例应变路径

采用AF-OW模型结合Chaboche准则对单轴路径和比例路径下正应力-正应变滞回环进行模拟,并与试验结果进行对比。由图4可以看出,316L不锈钢在单轴路径和比例路径下初始循环硬化的模拟结果与试验结果吻合较好,最大相对误差分别为2.1%和4.2%。对单轴路径和比例路径下前100周次内等效峰值应力演化进行模拟,并与试验结果进行对比。由图5可以看到,各路径下模拟得到的等效峰值应力约在第30周次达到饱和,进入循环稳定阶段。单轴路径和比例路径下模拟得到的最大等效峰值应力分别为304 MPa和331 MPa,与试验结果的相对误差分别为0.7%和1.8%。综上,将AF-OW和Chaboche各向同性硬化准则结合可以较准确地模拟单轴和比例路径下316L不锈钢的循环硬化行为。

图4 AF-OW模型结合Chaboche准则模拟得到单轴和比例路径下正应力-正应变滞回环与试验结果的对比Fig.4 Comparison of simulated normal stress-normal strain hysteresis loop by AF-OW model combined with Chaboche criterion and test results under uniaxial path (a) and proportional path (b)

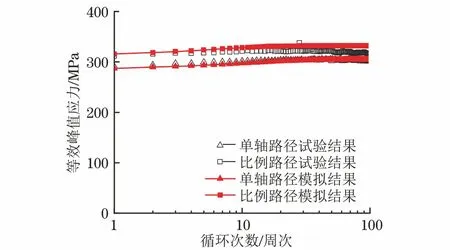
图5 AF-OW模型结合Chaboche准则模拟得到单轴和比例路径下等效峰值应力演化与试验结果对比Fig.5 Comparison of simulated evolution of equivalent peak stress by AF-OW model combined with Chaboche criterion and test results under uniaxial path and proportional path

3.3.2 非比例应变路径

采用将AF-OW模型和Chaboche准则结合的方法对十字路径和圆路径下的正应力-正应变滞回环和等效峰值应力演化进行模拟。由图6可以看出,模拟得到的十字路径和圆路径下的正应力-正应变滞回环与试验结果相差较大,最大相对误差分别为23.9%和28.8%。将非比例度的概念嵌入各向同性硬化准则对模型进行改进,模拟得到的十字路径和圆路径下的正应力-正应变滞回环与试验结果吻合良好,最大相对误差分别为1.3%和3.2%,结果如图7所示。

图6 AF-OW模型结合Chaboche准则模拟得到十字和圆路径下的正应力-正应变滞回环与试验结果的对比Fig.6 Comparison of simulated normal stress-normal strain hysteresis loop by AF-OW model combined with Chaboche criterion and test results under cruciform path (a) and circular path (b)

图7 改进模型模拟得到十字和圆路径下的正应力-正应变滞回环与试验结果的对比Fig.7 Comparison of simulated normal stress-normal strain hysteresis loop by modified model and test results under cruciform path (a) and circular path (b)

由图8可知:采用AF-OW模型结合Chaboche准则的方法模拟得到100周次内十字路径和圆路径下等效峰值应力演化结果与试验结果相差较大,模拟得到的最大等效峰值应力分别为473 MPa和497 MPa,与试验结果的相对误差分别为25.5%和36.4%;采用考虑非比例度的改进模型模拟得到十字和圆路径下的等效峰值应力演化结果与试验结果吻合良好,模拟得到的最大等效峰值应力分别为618 MPa和686 MPa,接近试验得到的最大等效峰值应力(622 MPa和681 MPa),相对误差分别为1.9%和1.2%,计算得到硬化率分别为40.2%和46.3%,接近于试验得到的硬化率(38.2%和44.6%)。可见,考虑非比例度的模型可以更加准确地描述多轴非比例载荷下的循环特性。

图8 AF-OW模型结合Chaboche准则和改进模型模拟得到十字和圆路径下等效峰值应力演化与试验结果的对比Fig.8 Comparison of simulated evolution of equivalent peak stress by AF-OW model combined with Chaboche criterion (a) and modified model (b) and test results under cruciform path and circular path

4 结 论

(1) 在等效应变范围为0.7%条件下,316L不锈钢在单轴、比例、十字和圆路径下的疲劳循环初期均产生了循环硬化,且等效峰值应力在循环次数为30周次左右达到饱和,随后进入循环稳定阶段;在单轴、比例、十字和圆路径下的硬化率分别为5.2%,4.5%,38.2%,44.6%,在十字和圆2种非比例应变路径下,316L不锈钢产生了明显的附加强化。

(2) AF-OW模型结合各向同性硬化准则可以准确地描述单轴和比例路径下的正应力-正应变滞回环和等效峰值应力演化,其中正应力-正应变滞回环的最大相对误差分别为2.1%和4.2%,最大等效峰值应力的相对误差分别为0.7%和1.8%,但是该模型对十字和圆路径下的模拟效果较差,相对误差均大于20%。

(3) 将非比例度的概念嵌入到各向同性硬化准则中后,该模型可以准确地描述十字和圆路径下的循环硬化特性,正应力-正应变滞回环的最大相对误差分别为1.3%和3.2%,最大等效峰值应力的相对误差分别为1.9%和1.2%。