煤矸分拣机械爪结构优化设计及有限元分析

张宝锋，王鸿飞，董雅文，宋栓军

（1.西安理工大学机械与精密仪器工程学院，陕西西安 710048；2.西安工程大学机电工程学院，陕西西安 710048）

0 前言

近年来，我国的煤炭行业一直处于高产量状态，而在实际生产中，原煤中夹杂着大量的煤矸石，由于煤矸石热值较低，需要将其分拣出去，同时挑选其中的劣质煤和黄铁矿［1］。但是煤矸石自动分拣过程中普遍存在矸石分拣机械爪抓取不牢固等问题，这在一定程度上制约了优质原煤的生产效率。针对手爪结构、受力和磨损等问题，有关学者进行了大量研究。

段念、范平清［2］设计一种煤矸分拣拨爪，主要依靠一根拨爪转动，实现将矸石从传送带拨出，这种方法需要煤和矸石整齐排列在传送带上才能实现分拣。郭大林等［3］设计一种煤矸连续分离装置，该装置提前将煤和矸石整齐排列在传送带上，利用两根拨爪进行分选，每根拨爪侧面安装耐磨橡胶板，在一定程度上减少了矸石对爪体的磨损，但不适用于大块煤矸石的分拣。王海舰等［4］设计一种煤矸分拣机械爪，该机械爪为三指抓取，虽然可以稳固抓取，但由于矸石大小不一，三指不便于抓取矸石。朱文博、陈建文［5］提出一种机械爪和拨爪配合使用实现煤矸分拣的装置，该装置整合了二者的优点，机械爪结构简单，但整体尺寸较大，运动不灵活。张军等人［6］设计一种夹持式机械爪，由两侧对称的4 根手指进行夹取，该机械爪抓取稳定，但未考虑机械爪耐磨问题。张勇等人［7］设计一种煤矸分拣机械爪，该机械爪体积适中，结构简单，可稳定抓取，但未考虑爪头耐磨性的问题。曹现刚等［8］设计一种煤矸机械爪，结构紧凑，可稳定抓取，同时在手指内侧安装橡胶衬垫，但耐磨性能较差，不能持续长时间使用。

现有煤矸分拣执行机构主要采用拨爪和夹爪两种方式。采用拨爪方式控制系统的设计，结构简单，执行效率高且动作少，但无法分离大块煤矸石；采用夹爪可以实现传送带上任意位置煤矸石的准确抓取，但存在抓取不牢固的问题，这会导致煤矸石中途掉落，影响抓取效率。另一方面煤矸分拣工作量较大，需要对煤矸分拣机械爪进行力学性能分析和结构优化设计，以保证机械爪抓取煤矸石时牢固、可靠，且具备一定的使用寿命。针对以上问题，本文作者以目前煤矸分拣生产线广泛采用的一种机械爪为研究对象，在建立三维模型的基础上，拟使用Adams 对机械爪进行运动分析和受力分析，对其结构进行优化设计，并结合优化后机械爪的受力分析结果，对主要构件进行有限元分析，以期改善煤矸分拣机械爪主要构件的力学性能，延长其使用寿命。

1 煤矸分拣机械爪受力和运动分析

1.1 煤矸分拣机械爪三维模型

煤矸分拣机械爪作为煤矸分拣系统的执行机构，其设计的好坏直接影响到最终的抓取效率。目前煤矸分拣生产线广泛采用的机械爪模型如图1 所示，该机械爪机构运动简图如图2（a）所示。机械爪采取两侧对称布置，每侧5 根手指，手指末端向抓取的一侧有少许弯折，便于抓牢煤矸石；固定块与手指相连，使手指一点固定；手指另一点之间穿插有连杆并通过一根两端有螺纹连接的细长轴连接；连杆另一端连接传动板，传动板与气缸的伸缩杆相连，通过伸缩杆上下移动带动传动板上下运动，从而使连杆和手爪产生相应的运动。

图1 煤矸分拣机械爪三维模型Fig.1 3D model of coal gangue sorting machine claw

图2 煤矸分拣机械爪机构简图Fig.2 Schematic of coal gangue sorting mechanical claw：（a）kinematic sketch；（b）force state of rod 3；（c）force state of rod 1

1.2 机械爪的机构受力分析

煤矸石的比重约为1.8 t／m3［9］，若抓取的煤矸石体积为200 mm×200 mm×100 mm，则一块煤矸石的质量m大致为7.2 kg。考虑到煤矸石中含有各类砂石岩，取摩擦因数μ＝0.48。在抓取煤矸石过程中，煤矸石对机械爪表面产生的反力为FN，夹持状态的保持完全靠煤矸石与机械爪之间的压力产生的摩擦力Ff，由Ff＝mg＝2μFN可得一侧机械爪所需的夹持力FN＝73.5 N。

如图2（a）所示，杆3 为输入端，驱动力为F，两侧连杆2 对杆3 的反作用力为F1和F2，其方向沿连杆2 指向杆3，并于水平方向夹角为α。

杆3 的力平衡条件如图2（b）所示，由∑Fx＝0，可得F1＝F2。由∑Fy＝0，得：

如图2（c）所示，设杆2 对杆1 的作用力为F′1，因为杆2 为二力杆，所以F′1＝-F1，由杆1 的力矩平衡条件：

当夹紧矸石时，α＝17.7°，β＝25.4°，c＝18 mm，b＝182 mm，代入公式（4）计算，可得驱动力F＝283 N。

使用SolidWorks 建立机械爪装配体模型并导入到Adams 中；修改相关系统设置，零件材料、单位制和重力等；添加运动副和约束，共设置15 个运动副和约束，其中包括2 个固定约束、12 个转动副和1 个移动副，添加10 根手指与物体之间的接触，物体与地面之间的接触。最终结果如图3 所示。

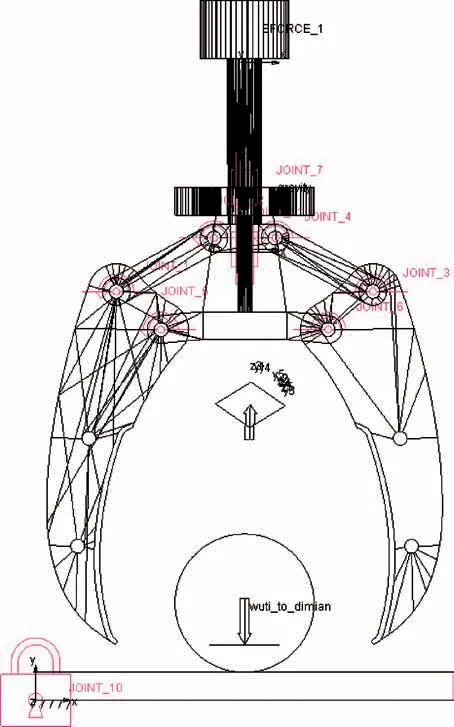
图3 Adams 仿真示意Fig.3 Diagram of Adams simulation

添加输入驱动力F＝283 N，假定夹紧时间为0.4 s，设定STEP 函数如下：

STEP（time，0，0，0.4，283）

在进行煤矸分拣时，还需将煤矸石从传送带抓起。为模拟实际效果，添加机械爪整体向上移动的驱动，设定STEP 函数如下：

STEP（time，0.4，0，1，100）

机械爪首先受到竖直向下的驱动力，在0.4 s 时完全夹紧物体，0.4～1 s 保持夹紧姿态且竖直向上运动。图4 为其中一根手指与煤矸石接触力的变化情况，可知：在0.4 s 之后，机械爪处于夹紧状态，单根手指夹持力稳定在15 N，所以一侧机械爪的夹持力为75 N，与理论计算结果相差不大。出现误差的原因是在理论计算时，为计算方便，个别角度取整数，所以存在少许误差。

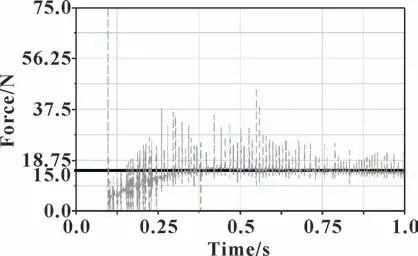
图4 单根手指接触力变化情况Fig.4 The contact force change of single finger

结果表明：仿真的夹持力与理论计算的夹持力基本吻合，所以，该机械爪能满足煤矸石的抓取要求。

1.3 机械爪的运动要求分析

对煤矸分拣机械爪的运动分析主要是分析机械爪末端的开合距离和活塞杆的行程，机械爪末端的开合距离决定机械爪可以抓取煤矸石大小的范围，活塞杆的行程可以确定气缸的大小。

Adams 仿真结果如图5 所示：机械爪在0～0.5 s从任意位置向中间靠拢，此时两手指之间可达的最小距离为12 mm；在0.5～1 s 时机械爪张开，到1 s 时最大开合距离为335 mm，即机械爪最大张开宽度为335 mm，该开合范围满足实际需求；0.5 s 时活塞杆位于气缸底端，此时活塞杆在参考坐标系中y方向的位置为38 mm；1 s 时活塞杆位于气缸顶端，此时活塞杆在参考坐标系中y方向的位置为98 mm，活塞杆的运动行程为60 mm。

图5 机械爪末端的开合距离和活塞杆的行程Fig.5 Opening and closing distance of mechanical jaw end and stroke of piston rod

2 煤矸分拣机械爪优化设计

2.1 参数化模型建立

文中优化目标是在不改变输入驱动力的情况下，通过改变构件结构参数，使机械爪的夹持力越大越好。优化前首先建立煤矸分拣参数化模型，通过已经建立好的模型确定各个铰链点在平面中的位置。获得各个关键点的坐标如表1 所示。

表1 参数化机械爪关键点坐标值Tab.1 Coordinates of key points of parametric mechanical jaw

由于机械爪为对称式，为了简化模型，在不影响优化结果的基础上仅取一对手指进行参数化建模。建立模型后，在连接处添加运动副，在传动杆处添加驱动力，添加两根手指与物体的接触力和物体与台面的接触力。参数化模型如图6 所示。

图6 煤矸分拣机械爪参数化模型Fig.6 Parametric model of gangue sorting mechanical jaw

2.2 设计变量分析

因为机械爪为对称结构，所以选择机械爪一侧的关键点作为设计变量即可，两侧关键点之间建立关系，使对称的两个点变化相同。由公式（4）可知：

所有的参数中对夹持力FN有影响的为b、c、α、β、F，F为机械爪的驱动力，在夹紧煤矸石时，认为是一个固定值。b为机械爪末端夹持力到固定铰链点的距离，由于煤矸石大小不一，距离b依据煤矸石大小的不同而发生变化，关键点E、G、I、K的变化均会引起b的变化。参数c、α、β均与铰链点A和C有关，铰链点A和C位置变化将引起c、α、β的变化。所以机械爪一侧的6 个关键点根据需要作为设计变量，由于该机械爪为对称结构，此次优化以左侧为主要设计变量，右侧变量与左侧变量建立对应关系，以A、B两点为例，如表2 所示。

表2 A、B 两点设计变量关系Tab.2 Design variable relations between points A and B

接着确定各个变量的优化范围。以DVA_X 为例，该设计变量表示的是关键点A的横坐标，选择变量的类型为Real（实数）。当DVA_X 在指定范围内变化时，取目标结果最优条件下DVA_X 的值作为最优值。

该优化主要以左侧关键点为设计变量，各个设计变量均在原来的基础上变动。由于关键点A和C的影响参数较多，所以A和C两点的变化范围取得较大，便于观察其对目标结果的影响；关键点E、G、I、K影响b，同时也决定了手指的结构，对这4 个点的变化范围取得较小，避免优化后手指结构变化较大，不利于实际抓取。

进行Design Study 确定各个设计变量对目标优化结果的敏感度，让敏感度较高的设计变量参与优化，忽略敏感度低的设计变量，加快计算速度。敏感度Si的公式如式（5）所示：

式中：O为目标优化结果；V为设计变量；i为迭代次数。

图7 为对设计变量DVA_X 进行Design Study 的仿真结果，Sensitivity 一栏为设计变量DVA_X 对目标优化结果的敏感度。DVA_X 一栏表示的是连杆的长度，所以其绝对值为杆的长度。DVA_X 的大小对夹持力的影响如图8 所示，可知：末端夹持力随着DVA_X（连杆）的增大而减小。

图7 变量DVA_X Design Study 仿真结果Fig.7 Variable DVA_X Design Study simulation results

图8 接触力随设计变量DVA_X 的变化曲线Fig.8 The variation curve of contact force with design variable DVA_X

相似地，判断所有主要设计变量对目标优化结果的敏感度，最终选定的设计变量为DVA_X、DVC_X、DVE_X、DVG_X、DVI_X、DVK_X。

2.3 结构优化设计

优化分析与Design Study 不同之处在于设计变量需要选择多个，考虑多个变量变化时，使目标优化结果最优。这里输入Design Study 中分析出的几个对结果敏感度较大的设计变量进行优化分析。

选择算法OPTDES-GRG（Generalized Reduced Gradient，广义简约梯度法）进行优化，其通用性、有效性和可靠性在处理非线性优化问题具有优势。该算法的主要特点是寻优时沿边界进行计算，而结构优化的解往往在边界上。该算法求解的实质是通过变量的隐式消元，转化为无约束极值问题处理，是目前求解一般非线性优化问题的最有效算法之一。

广义简约梯度法［10］求解的非线性问题如式（6）所示：

式中：H（X）＝［h1（X），h2（X），…，hm（X）］T，L＝［l1，l2，…，ln］T，U＝［u1，u2，…，un］T。

在求解时，先将X的全部分量分解为2 部分，如式（7）所示：

式中：XB为基向量，m维；XN为非基向量，n维。

相应地，将L和U的全部分量分解为两部分。

由隐函数存在定理知，存在连续映射如式（8）所示。

目标函数F（X）转化为

于是，原来n个变量的目标函数F（X）变为n -m个变量的函数f（XN），则f（XN）在Xk关于XN的梯度即为简约梯度。

则F（X）关于XN的简约梯度为

简记简约梯度

运用Adams 中的Optimization 功能完成优化，优化前后各个设计变量取整后如表3 所示。结合表3 和图6 可知，传动杆和固定块的参数没有发生变化，连杆的长度变长，手指外观有微小变动。

表3 设计变量优化前后对比 单位：mmTab.3 Comparison of design variables before and after optimization Unit：mm

优化后末端夹持力如图9 所示：在稳定抓取时，优化前机械爪的夹持力为15.1 N，优化后机械爪的夹持力为24.5 N，约增加了62%，使机械爪末端的抓取更加牢固可靠。

图9 末端夹持力优化前后对比Fig.9 Comparison of end clamping force before and after optimization

3 煤矸分拣机械爪有限元分析

在进行Adams 动力学分析时，分析结果显示连杆两端受到的力较大，并且手指是与物体直接接触的构件，所以，有必要对连杆和手指进行静力学分析，判断在夹紧状态下，构件的强度是否满足使用要求。通过Ansys Workbench 对构件进行静力学分析，可以看出构件的应力和变形情况，进而对零件的强度进行评估，为后续优化提供参考。

3.1 连杆有限元分析

连杆使用的材料为结构钢，首先将在SolidWorks中建好的连杆模型导入Ansys Workbench 中，在导入之前对构件做简化处理，压缩掉不必要的倒角、圆角和孔等特征。选择静力学分析模块，定义材料为Q345，主要参数如表4 所示。

表4 Q345 材料属性Tab.4 Q345 material properties

定义网格大小为2 mm，在圆孔处细化处理。定义两圆孔处施加两个压力。网格划分结果和边界条件约束如图10（a）所示。

图10 连杆有限元分析Fig.10 Finite element analysis of connecting rod：（a）mesh division results and boundary condition constraints；（b）stress and deformation

对连杆的应力分布和变形分布进行分析，如图10（b）所示。在机械爪夹紧煤矸石时，从应力分布云图可以看出，连杆应力最大处为圆柱面与杆身过渡处，此时最大应力为2.051 6 MPa；从应变分布云图可以看出，连杆变形最大处为两端圆柱面的端面，此时最大变形为5.761 5×10-5mm。所以，在夹取煤矸石的过程中，连杆的应力和变形均在合理范围内，满足实际使用要求。

3.2 手指有限元分析

手指使用的材料为结构钢，定义网格大小为2 mm，在圆孔处细化处理。外侧圆孔施加固定约束，内侧圆孔添加力约束，由于煤矸石大小不一，手指与煤矸石接触的部位取接触概率较大的表面。网格划分结果和边界条件约束结果如图11（a）所示。

图11 手指有限元分析Fig.11 Finite element analysis of finger：（a）mesh division results and boundary condition constraints；（b）stress and deformation

对手指的应力和变形进行分析，如图11（b）所示。在机械爪夹紧煤矸石时，从应力分布云图可以看出，手指应力最大处为圆孔固定约束处，此时最大应力为4.057 4 MPa；从应变分布云图中可以看出，手指变形最大处为手指头部，此时最大变形为2.089 4×10-3mm。所以，在夹取煤矸石的过程中，机械爪的应力和变形均在合理范围内，满足实际使用要求。

3.3 机械爪整体结构有限元分析

在对机械爪的主要构件进行分析之后，本文作者对机械爪整体结构进行应力应变分析。首先，添加材料Q345，为连杆添加材料属性，再导入模型，压缩掉螺母、螺钉等不影响分析结果的零部件，保留结构的主要部分；定义各个构件之间的约束，进行调试确保正常运动；主要受力构件的网格大小为5 mm，单元类型为四面体单元；添加机构的驱动力和煤矸石对手指的压力，整体分析时将手指与煤矸石的接触设置为手指表面整体接触，定义支撑板为固定支撑，网格划分结果和边界条件约束如图12 所示。

图12 机械爪的网格划分结果（a）和边界条件约束（b）Fig.12 Mesh division results（a）and boundary condition constraints（b）of mechanical claw

对机械爪整体应力和变形进行分析，如图13 所示。机械爪抓取煤矸石时，从应力分布云图中可看出：机械爪应力最大处为连杆与手指接触的部位，最大应力所处部位与连杆和手指单独分析时一致，最大应力为3.158 1 MPa；从应变分布云图中可看出：机械爪变形最大的地方在手指头部，与手指分析结果接近，最大变形为4.060 9×10-3mm。

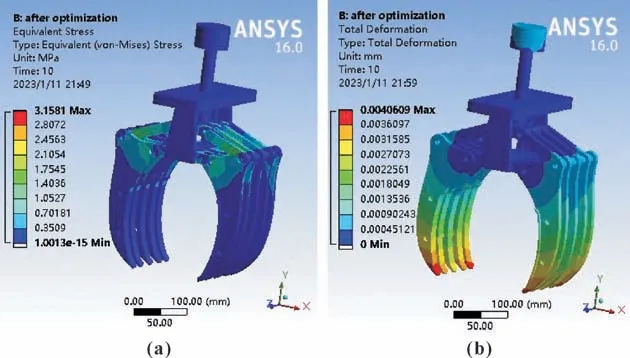
图13 机械爪的应力（a）和变形（b）Fig.13 Stress（a）and deformation（b）of mechanical claw

因此，在夹取煤矸石的过程中，机械爪的应力和变形均在合理范围内，满足实际使用要求。

4 结论

分析煤矸分拣机械爪存在的问题，建立目前煤矸分拣生产线广泛采用的一种机械爪三维模型，进行机械爪末端理论受力计算，并与Adams 仿真结果进行对比，仿真结果与理论计算结果一致；进行运动分析得出机械爪末端最大张开宽度为335 mm，满足抓取要求，得出活塞行程为60 mm，便于气缸选型；进行优化设计，在不改变驱动力的情况下，通过改变各个设计变量使得机械爪末端的夹持力最大，使机械爪抓取更牢固；使用单侧机械爪关键点数据建立参数化模型，创建设计变量，分析各个设计变量的敏感度，提取敏感度大的设计变量进行优化分析，优化之后夹持力提升了约62%。最后，结合Adams 动力学分析结果和ANSYS Workbench 对连杆、手指以及机械爪整体结构进行应力分析，结果表明，优化之后机械爪满足使用要求，且力学性能有了显著提高。