不确定性分布式电源优化配置分析

戚思源 吴文龙 周 艳 朱 慧

（国网江苏省电力有限公司盐城市大丰区供电分公司）

0 引言

当前，我国电力系统主要采用大电网、大机组、高电压的配电方式。这种配电方式可靠性相对较差，供电欠缺灵活性，且无法充分满足配电网终端的电能需求，容易受到各方面因素的干扰，甚至可能出现系统大面积瘫痪的问题。随着社会对电能需求不断提高，对电能质量要求不断提升，大型电力系统的运行呈现出越来越明显的弊端，而若是采用增大输送容量的方式，满足电能增长需要，势必会造成运行难度大、损耗高、环境污染严重等问题。要想解决此问题，接入分布式电源具有重要作用。

1 分布式电源接入对配电网的影响

分布式电源主要包括风力发电和光伏发电。其中，风能作为可再生能源，其发电方式主要有独立发电、并网发电和其他方式互补；光伏发电是太阳能直接应用的形式，主要有集中式光伏发电、分布式光伏发电。

分布式电源在配电网中接入，向接入节点负荷直接注入功率，会使得配电网原本的潮流分别出现变化，一定程度上影响系统网损，而其影响效果则由分布式电源在配电网中的接入位置、容量和节点负荷等因素决定。通常情况下，若配电网系统中的各节点负荷均比节点所注入的分布式电源功率要大，那么分布式电源的接入就能够减轻系统网损，相反则会使得局部支路或整个系统网损升高。当分布式电源接入电网的总容量一致，但各节点容量分配不同，那么网损效果也不同，往往接入节点位置越靠后，越会减轻系统网损程度。

此外，分布式电源的接入，还会影响配电网的电压分布情况。在配电系统当中，电压随着配电网馈线潮流方向逐渐降低，各节点对负荷的需求各不相同，网络中电压分布也会有所不同。一般来说，沿着配电网潮流输送的方向，节点电压不断下降，所以线路的末端电压最低，可能会影响电网运行的安全性。在分布式电源接入后，在接入位置向系统节点注入无功功率和有功功率。其中，无功功率能够在一定程度上支撑节点电压，使节点处电压升高，若功率过大，则容易出现潮流倒送的问题，使得电压超标；有功功率则可以有效减小线路输送容量，对电压分布产生影响［1］。

2 不确定性分布式电源优化配置

2.1 不确定性多场景分析

多场景分析，主要解决无法通过数学模型加以描述的不确定性问题，其重点在于以一定规则基础，枚举不确定变量，将其问题分析变成多个确定性问题分析，保证问题解决准确性。若生成的场景规模越大，则意味着不确定性问题描述越精准，若场景规模较小，则可能会遗漏其中部分代表性场景，精准度变低。

分布式电源主要包括风力发电和光伏发电。以往在研究分布式电源时，大多研究其负荷需求和出力值，但事实上，无论是风力发电还是光伏发电，都容易受到地理位置和区域气候等因素影响，在向配电网供能时，功率基本无法保持恒定，而是会在环境变化下，不断改变出力效率，实际的负荷需求也并非完全一致。所以，在研究分布式电源优化配置时，还需多加研究实际出力和负荷需求波动等情况。

预测风力发电有功功率难度相对较大，其出力容易受到所处位置风速影响，凭借二者之间的关系，可得出风力发电有功功率。利用不确定性概率模型，获得风机出力值，风速符合两参数Weibull分布，其函数模型如下：

其中，v、k、c分别为实际风速、Weibull分布函数形状参数和尺度参数。当概率模型参数不同时，出现风速最大概率时，所对应的风速也各有不同，产生的最大风速也可能存在不同。此外，风机实际有功出力，与其所处位置的风速大小也有关联。若风速小于切入风速或大于切出风速时，风机的实际输出有功功率为0，此时由于风速过低或风机运行不安全，导致风机无法正常运行；若风速大于切入功率、小于切出功率时，那么风机实际有功出力则与风速之间呈线性关系，风速不断加大，风机的输出有功功率也会随之加大；若风速大于切出功率、小于切入功率时，风机稳定运行，此时有功出力则为额定输出功率［2］。

光伏发电的实际出力，主要受光照强度的影响。根据光照强度概率模型，在不同的Beta分布参数下，产生的光照强度分布概率密度函数各不相同。参数影响密度函数曲线形状，影响光照强度概率分布情况。光伏的实际有功出力，随着光照强度发生变化。通常情况下，当光照强度小于额定光照强度时，光伏发电机实际有功出力和光照强度之间呈线性增长关系；当光照强度大于额定光照强度时，太阳能电池组件达到最大发电功率，光伏有功输出也会保持恒定。

2.2 多场景分析下的优化配置模型

以风力发电、光伏发电为基础的分布式电源，能够有效保证经济性和环保性指标效果，以经济性角度，构建分布式电源优化配置模型，并考虑其所带来的环境效益。

规划分布式电源时，主要考虑四个约束条件，分别为电流、电压、潮流和安装容量约束。分布式电源优化配置模型的构建，属于典型的约束性规划问题，可运用传统数学规划法和群体智能优化法进行计算求解。在本文研究中，主要采用粒子群算法，以群体间信息共享，寻找最优解。粒子群算法应用中，首先初始化粒子群算法种群参数，对各参数的粒子适应度函数值计算，对其大小进行排列，选择个体和全局最优粒子。根据计算结果，更新粒子位置和速度，判断计算过程是否完成，输出最优解。

针对粒子算法进行改进，主要改进其中的惯性权重因子，以此提高粒子群算法在迭代前期的全局搜索能力和后期的局部收敛性能，提高求解过程的收敛速度。同时，引进遗传算法中的交叉变异思想，增加种群多样性，加大最优解跳出的可能性［3］。粒子群算法中的重要参数之一即为惯性权重因子，其体现粒子在寻优过程中达到整体状态。在前期，为搜寻最优解，粒子群搜索空间应尽量扩大，提高其全局搜索能力，在迭代后期，则快速收敛到最优解，此时惯性权重因子需减小。

遗传算法，以人工演化为基础，得出的随机搜索算法。这一算法的基本思想，是以适应度函数值为基础，构建种群淘汰机制，对种群进行筛选，将其中的最优种群作为最优解。遗传算法在迭代过程中，全局搜索能力更强，其具有一定的变异能力，但局部搜索能力相对较差。所以，在改进算法过程中，适当运用遗传算法的选择、变异操作、交叉等功能，将其应用到粒子群算法当中，提高粒子群算法全局搜索能力和收敛精度。

粒子群算法寻最优解的过程中，需要利用群体间的信息共享，确保粒子始终向最优解方向移动。在此改进优化下，粒子收敛速度更快，且可有效避免最优粒子由于交叉变异等操作出现丢失问题，确保保留最优粒子并继承［4］。若同时有多个粒子为最优粒子，为确保其全局搜索能力，可限制保留的粒子个数，以此更好地发挥遗传算法操作性能。

2.3 分布式电源优化配置

根据以上优化配置模型和粒子算法改进，从三种方案中确定最优的分布式电源优化配置方法。其中，方案1为不安装分布式电源；方案2为在待选节点上安装分布式电源；方案3为在待选节点上安装分布式电源，并且考虑源荷的不确定性影响。如表1所示，为不同方案下分布式电源规划结果。其中，表中的4（0，5）所表示的为在电网系统节点4位置安装0台风机和5台光伏。

表1 不同方案下分布式电源规划结果

通过三个方案对比分析，发现在分布式电源并网后，会产生一定的费用投入，但综合费用仍然比不接入分布式电源时要低。究其原因，主要在于接入分布式电源后，相当于配电网中的节点负荷需求下降，线路传输功率有所减小，所以系统的网损费用和上级电网的购电费用均会有所减少。通过方案2和方案3对比分析，加入不确定性考虑后，分布式电源优化配置会更加合理。这主要由于分布式电源在并入电网后，节点大概分别在于线路末端靠近的位置，由于输送容量变多所产生的网损有所减小，在末端负荷注入无功功率可有效改善末端的电压情况［5］。

加入不确定性因素进行考虑时，所得到的方案综合费用更低，与实际情况更相符。在此基础上，分析不同方案对配电网电压分布的影响。在电网中接入分布式电源后，向待安装节点注入无功和有功功率，可一定程度上支撑节点电压，并考虑不确定性源荷对电网电压分布的影响。

为进一步证明改进的粒子算法在分布式电源优化配置中的有效性，将其与基本粒子群算法和混沌粒子群算法进行对比分析，得出不同算法下的规划结果，如表2所示。

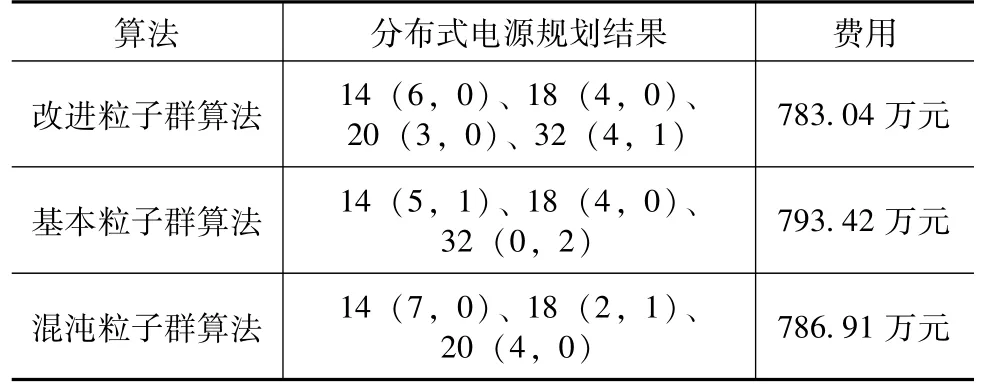
表2 不同算法下的规划结果

通过上述对比分析，发现在不同算法下，通过改进粒子群算法所得到的分布式电源规划结果更优，所使用的费用最少，这就意味着，通过改进粒子群算法，能够在考虑源荷不确定性的基础上，保证更高的精度，所得到的接入方案也更加具有经济性。

3 结束语

综上所述，本文根据分布式电源的特征和对配电网的影响，分析探究了不确定性分布式电源的优化配置方法。通过采用改进粒子群算法，结合遗传算法的方式，提高最优解找寻效率。并且，经研究发现，在待选节点上安装分布式电源，并且考虑源荷的不确定性影响可有效达到优化配置效果。