一种基于USB 摄像头QR 码识别优化算法

孙洪涛，李炎，李望荣

（1.歌尔股份有限公司，山东潍坊，261006；2.潍坊歌尔电子有限公司，山东潍坊，261021）

0 引言

随着QR（Quick Response）码新兴技术的不断发展，其本身具有储存量大、保密性高、追踪性高、成本便宜等特性，使得在手机支付、身份识别、物流追踪等领域得到了广泛的应用[1]。

针对精密件QR 码的定位与识别技术已经被大量研究和开发。其中，对于二维码的成像失真现象问题，刘宏伟[2]提出了一种基于Hough 变换的校正算法，最终实现了对QR码的定位，但缺陷在于，该算法无法实现对二维码在曲面环境下的变形处理。甘岚[3]等人提出了一种基于亚像素边缘检测的QR 码识别算法，该算法解决了QR 码因边缘模糊导致的识别率下降的问题。李军[4]采用扫描边界点来确定畸变控制点的方法，实现了对QR 码的曲面变形校正，能够显著提高识别率。考虑到生产车间的组装实际环境和使用成本，基于图像处理方式，需要结合具体场景进行定制算法开发。

结合以上研究，本文基于USB 摄像头硬件平台，提出一种针对生产车间精密件的视频数据、低图像质量的二维码的识别优化算法，并进行开发实现与测试。

1 算法流程

结合现阶段生产车间的采集设备硬件条件和QR 码应用条件，提出了一种QR 码图像预处理的算法。本算法的处理流程如图1 所示：（1）通过对二维码图像进行灰度预处理，统一各类型摄像头的图像输入格式；（2）通过ROI 标定，选择二维码所在区域，使后续分析处理时重点关注该区域，提升图像处理流程的整体效率；（3）通过去噪解决摄像头分辨率过低以及图片放大后引入的噪点，提升解码率；（4）自适应二值化：通过二值化算法突出二维码有效信息，提升解码率，并通过设计自适应策略来提升图像处理速度；（5）解码部分采用第三方工具，输出文本格式的ID。

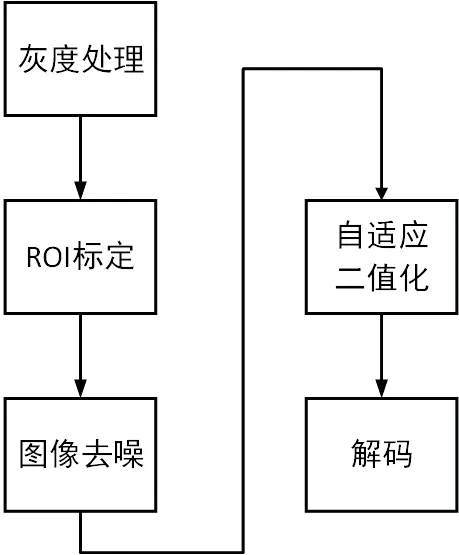
图1 算法流程图

2 算法实现

■2.1 图像预处理

2.1.1 灰度处理

彩色摄像相机录入的彩色的二维码图像包含R（红色）、G（绿色）、B（蓝色）三个分量，其中每个分量都有256个取值，即0 ≤R ≤255，0 ≤G ≤255，0 ≤B ≤255，灰度化则是将每一个像素点划定为0～255 范围中的一个确定的灰度值，由于二维码本身有效信息只有黑白两种色块，所以通过这样的操作并不会减少后续处理精度，并可以减少后期算法的运算量。灰度计算公式W 为：

另一部分USB 摄像头设备可以设置在拍摄时采用灰度模式从而直接获得灰度图像，如此灰度化操作便可以由硬件完成，减少了软件处理图像的环节。

2.1.2 ROI 标定

感兴趣区域（ROI）是从图像中选择一个图像区域，该区域内的数据是后续分析处理时重点关注的部分，对于部分固定位置的扫码场景，ROI 定位尤其重要。

由于在实际生产车间中测试工装及各类型硬件的位置相对固定，所以每次二维码出现的位置在图像中所占区域也相对固定，故一次选取ROI 区域后即可保存设定，后续图像自动使用此参数，通过ROI 定位来初步定位目标图像中的QR二维码，绿线即为认为标定的二维码区域，如图2所示。

图2 定位目标图像中的QR 二维码

经测试，合理地设置ROI 选区，可以在测试中使图像处理的速度提升4%左右，对提升算法整体效率具有一定的作用。

2.1.3 图像去噪

在得到灰度图像之后，对于低分辨率摄像头，有部分噪声满足泊松分布的盐粒噪声[5]，尤其是在成像质量不高或二维码本身比较小的情况下，此类噪音对于最终解码性能的具有一定的影响[6]，这便需要对图像进行去噪处理。

LabView 支持的IMAQVision 工具包中提供了多种滤波器，其中包括高斯滤波器、低通滤波器以及中值滤波器等方法[7]，经过实际测试，在上述滤波方法中，中值滤波效果最为显著，可以有效降低干扰噪声，并且保护原始信号，得到明显的平滑效果，故采用中值滤波。

中值滤波是一种较为常见的非线性处理方法，一般会采用图像中像素点及周围临近的像素点，并把像素值进行排列，取中值像素值作为当前像素点的数值。该方法运算简单，易于实现，可消除图像中孤立的噪声点，又可产生较少的模糊。在处理相机采样导致的噪声时，一般情况下中值滤波的处理效果要比邻域均值处理的低通滤波效果要好。以640×480 的低分辨率USB 摄像头为例，经测试，在都不使用后置算法的前提下，滤波去噪可以改善后续解码环节，提升2%左右的精准度。

■2.2 自适应二值化

由于二维码图像是由一系列的黑白码块组成，故利用黑色实线以及黑白切换的辅助线或定位块来定位，实现二维码信息图像在灰度级上两极分化，从而突出二维码图像信息，过滤其他灰度图形对定位处理带来的干扰。

在LabView 中调用IMAQImage2ArrayVI 函数把滤波后图形中的所有像素的点转化为二维数组，在循环中设定一个阈值，大于该阈值的点输出255，小于该阈值的点输出0，最后通过IMAQArray2ImageVI 函数即可将二位数组转化为二值化图像。

2.2.1 处理模式

算法的性能瓶颈就发生在本“二值化”环节，所以为了提升算法处理速度，在本环节设计了两种处理模式：“普通模式”和“光照修正模式”[8]。对于成像良好的图像采取“普通模式”进行处理，对于成像较差无法正常识别的图像采取“光照修正模式”进行处理，“光照修正模式”引入了局部阈值方法，在亮度较高的区域，考虑使用较大的阈值进行分割，而在亮度较小的区域，考虑使用较小的阈值进行分割，以便实现对一幅图像中不同亮度区域进行有效的二值化操作。同时，通过一定的策略来自动的调整内部参数，自动确定二值化阈值[9]。

2.2.2 原二值化算法的问题

LabView 中NI Vision 模块中的两种局部阈值法都有一些缺点，导致其不太适合直接应用于产线环境：

（1）一种是使用最大类间方差法的背景纠正法，背景纠正法先通过像素与邻域内的灰度均值做减法运算，来消除光照不均对图像的影响，然后再使用最大类见方差法计算局部阈值。它的缺点是在图像和背景灰度差异明显时会丢失图像细节，容易导致处理过后的二维码边缘难以识别。

（2）另一种是Niblack 二值化算法，基本思想是对每一个像素点都计算其邻域内的均值m(x,y)和方差s(x,y)，随后每个像素计算公式如下：

其中k 为修正系数，最终以T(x，y)的值作为阈值来二值化图像。Niblack 算法虽然能够实现图像的二值化，但是如果选取的区域均为背景点时，该算法会将灰度值较高的点当做是目标点，导致伪噪声的引入，同时由于每个像素都要计算邻域的均值和方差，所以Niblack 法的计算量很大，只适合用作单张照片的二值化处理，无法应用于视频环境。

2.2.3 基于比例系数的混合阈值法

本文通过参考最大类间方差法和只计算像素邻域均值的局部阈值法，提出了基于比例系数的混合阈值法。设最大类间方差法得到的整体阈值为t1，局部阈值法的阈值为t2，邻域内的综合阈值为T，比例参数为scale，则T 可以表示为：

其中，scale 取值范围是从0 到1 的数，通过调节scale 来获取合适的阈值。当scale 取0.4 时，二值化效果如图3 所示，可以看出二值化后，图形中重要细节明显增强，从根本上改善了视觉质量，二维码信息几乎没有细节丢失，并且算法的计算量得到了控制，可以支持20 帧每秒的视频检测速度。

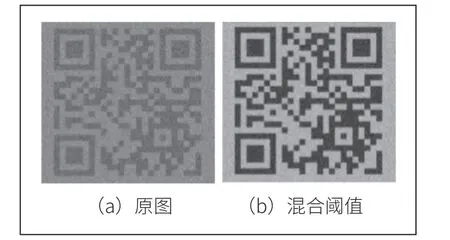
图3 二值化效果图

2.2.4 自适应策略

自适应策略表现为两点：（1）算法将在默认情况下采取“普通模式”进行二值化处理，只有在普通模式处理二维码无解析结果时，切换为“光照修正”模式继续进行处理。（2）在算法切换为光照修正模式后，可以自动调节scale 参数，来应对不同光照不均程度的图片。

为了测试出最适合解决产线环境所产生的干扰的scale值，本部分做了以下工程化可视化的操作：首先对scale 的合理区间进行初步的统计，方法是在算法内将scale 值设置为开放接口，可于界面上实时调节，用于查看不同scale 值对于图像解码率的影响。经测试不同的scale 值对应着这200 张照片不同的平均解码率，scale 在小于等于0.2 时解码率较低，而在0.8 以上解码率也会有一定程度的降低，如表所示，所以根据此结果认定scale 区间设置为0.2～0.8 之间比较合适车间环境。

表1

3 实验结果与分析

在测试数据获取方面，数据来源自640×480 分辨率的USB 摄像头生产车间实拍照片。测试数据获取过程不使用算法处理，将无法直接解码的图像列为受光照不均干扰影响较大的图片，记为“光照不均数据集”，当极端数据集的数量达到200 张后，统计当前总图像数为42022 张，记为“常规数据集”，其中成像良好的图像数量占41822 张。

■3.1 光照不同对比测试

本测试将分为两部分进行验证，（1）对光照不均数据集进行单独测试，检测算法对于处理干扰的有效性和效率；（2）对常规数据集进行测试，检验算法对于扫码模块正常运行时精准度的实际提升率。不同阈值算法对于解码效果的对比，本算法中的自适应处理机制，提升了算法整体效率，可达到99.91%，符合处理帧数20 帧左右每秒的设计要求。

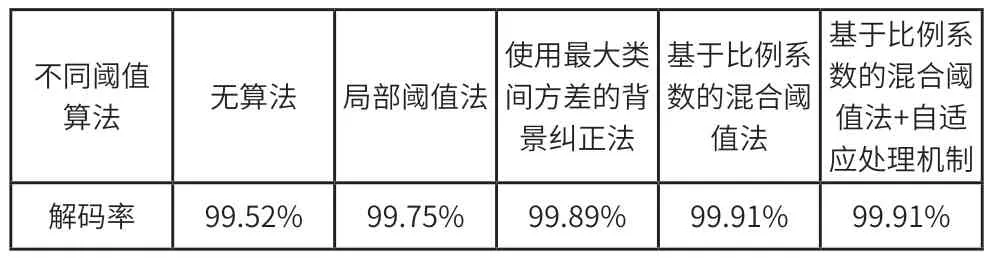
表2

■3.2 设备对比测试

通过对比使用USB 摄像头扫码的系统和传统采用扫码枪进行扫码的系统，来评价本系统的误检率，实际测试结果如图4 所示。

图4 系统测试误检率

在测试批次小于等于16 万次时，测试系统可正常运行，测试批次大于等于17 万次时，本系统的误检率超出业务规定要求，但已满足系统硬件在业务上要求10 万批次内正常运行测试误检率在0.1%以内的要求。为了避免误差的积累，系统均会在10 万测试批次后进行检修维护。总体来讲，基于USB 摄像头扫码的本系统，固然在硬件价格上低于公司传统使用扫码枪扫码的系统，但也带来了一定程度的测试误检率的提升，不过仍符合业务标准，系统具有可用性。

4 结论

由于在生产环境中存在外界因素的干扰，本文采用基于比例系数的混合阈值法+自适应处理机制方式，得到较高的QR 识别率。通过与扫码枪识别性能对比，减少了识别成本，具有良好的稳健性，为工程应用提供了新的算法方案。但由于自适应二值化部分对于不同精密件的适配度并不理想，因此在今后的研究中，需要进一步丰富和完善算法模型。