沙漠砂PE纤维ECC的拉伸性能与本构模型研究*

郑志超，韩风霞,2†，刘继颜

（1.新疆大学建筑工程学院，新疆 乌鲁木齐 830017；2.新疆建筑结构与抗震重点实验室，新疆 乌鲁木齐 830017）

0 引言

超高韧性水泥基复合材料（ECC）是一种具有高延性、高韧性、抗冲击性能良好和多裂缝开展特征的纤维增强水泥基复合材料，与普通混凝土及其它高性能混凝土相比，ECC在结构承载力、变形能力和能量耗散吸收等方面更为优秀.但ECC相较普通混凝土而言，其碳排放量与工程造价均较高[1].针对这一问题，国内外学者使用粒径较大的细骨料替代硅砂，以及使用高炉矿渣、硅灰等替代部分水泥等手段解决碳排放量和工程造价等问题.Guan等[2]利用粗河砂替代硅砂制备了极限拉应变大于9%并呈现应变硬化和多裂缝开展行为的ECC；Yu等[3]利用高炉矿渣和硅灰替代部分水泥制备了极限拉应变为8.7%的超高性能ECC.为了进一步降低ECC的制作成本，遵循原材料本地化的原则[4]，使用中国新疆本地沙漠砂替代部分天然砂制备ECC.由于沙漠砂粒径小，掺入后可以改善砂骨料的级配，使纤维更好地在基体中分布，从而增强PE-ECC试件的拉伸性能.

单轴拉伸应力-应变关系是ECC最基本的本构关系，可以反映ECC受力阶段的破坏过程和变形特点[3].国内外学者针对ECC受拉性能及本构关系开展了一系列试验及理论研究[5-10].Kanda等[11]提出了仅考虑弹性阶段和应变硬化阶段的双线性模型，并未对软化阶段进行描述.张聪等[12]通过引用混凝土断裂力学和细观力学的概念，提出了用于SF-PVA/SHCC（钢纤维与PVA纤维混杂增强应变硬化水泥基复合材料）的单轴拉伸三线本构模型.姚淇耀等[13]提出了以强化段和软化段来描述SECC拉伸应力-应变关系的波动上升段和下降段，并得到适用于SECC的三线拉伸本构模型.虽然国内外学者针对ECC提出了很多种本构模型，但尚未形成统一的认识，对沙漠砂PE-ECC的拉伸本构模型也少有研究.

综上所述，基于课题组前期所得配合比及其相关研究的基础[14-15]，使用新疆本地原材料沙漠砂替代部分天然砂，制备哑铃型试件并进行单轴拉伸试验，分析不同聚乙烯（PE）纤维体积掺量和水胶比两种因素对PEECC拉伸性能的影响规律，建立其拉伸本构模型，并进行验证分析.

1 试验研究

1.1 原材料

制备沙漠砂PE-ECC试件的原材料为：P·O 42.5级水泥；Ⅱ级粉煤灰；天然砂与沙漠砂混掺，沙漠砂的成分如表1所示；聚羧酸系高性能减水剂，减水率为21%，含固量为12%；由中国山东莱芜特力夫纤维制造厂研发的PE纤维，物理性能指标如表2所示.

表1 沙漠砂化学组成成分质量百分比

表2 PE纤维物理性能指标

1.2 试件设计

以纤维掺量及水胶比为变量，制备沙漠砂PE-ECC单轴拉伸试件，试件编号及配合比如表3所示.沙漠砂PEECC的制作流程为：将胶凝材料与砂称好后放入搅拌桶中搅拌2～3 min，使其分布均匀.然后加入1/3的水和减水剂搅拌1 min，再加入1/3的水和减水剂，搅拌2 min；最后加入剩余的水、减水剂和增稠剂，使其呈现良好的流动性；最后边搅拌边缓慢加入PE纤维，将拌好的拌合物分别放入刷油的哑铃型亚克力模具中浇筑并振捣，24 h后脱模，并在标准养护室内养护28 d.

表3 PE-ECC配合比/g

1.3 拉伸试验

拉伸试验设备选用型号为LDS-5的液晶显示电子拉力机，采用位移式自动控制加载，加载速率为0.5 mm/min，在试件测试段放置LVDT采集位移数据，位移数据采集频率为3次/秒.试件尺寸及拉伸装置示意图如图1所示.

图1 试件尺寸及拉伸装置示意图

2 试验结果与分析

通过单轴拉伸试验得出沙漠砂PE-ECC应力-应变曲线，如图2所示.其中初裂应力、极限拉应力、极限拉应变及拉伸韧性结果如表4所示.由图2、表4可知，随着纤维掺量的增加，对沙漠砂PE-ECC试件的拉伸性能产生有利影响，但是纤维过多则不利于纤维在基体中均匀分布，对沙漠砂PE-ECC试件拉伸性能造成不利影响；水胶比的增大有利于纤维在基体中均匀分布，对沙漠砂PE-ECC试件拉伸性能产生有利影响，但是水胶比过大则会削弱纤维与基体之间的摩擦黏结力，对沙漠砂PE-ECC试件拉伸性能造成不利影响.

图2 PE-ECC拉伸应力-应变曲线

表4 单轴拉伸试验结果

试验过程中，由于PE纤维的抗拉强度较高，试件破坏时纤维被拔出，纤维拔出长度与纤维直径有关.一般情况下，随着纤维长径比的增大，纤维与基体之间的摩擦力增大，从而增加试件的初裂应力、极限拉应力、极限拉应变与拉伸韧性.本文仅研究纤维掺量及水胶比对PE-ECC拉伸性能的影响规律，未量化纤维长径比对PE-ECC拉伸性能的影响.

1）初裂应力

由图3、表4可知，初裂应力随着纤维掺量的增大而变大，相较PE-0.25-0.5试件，纤维掺量为1%、1.5%、2%、2.5%时初裂应力分别提高了27%、29%、43%、66%.上述结果表明：当纤维掺量较多时，可以降低沙漠砂PEECC试件的初始缺陷尺寸，提高初裂应力；初裂应力随着水胶比的增大而减少，相较PE-0.25-1.5试件，水胶比为0.28、0.31、0.34时初裂应力分别减少了8%、19%、23%.可能是随着水胶比的增大，基体颗粒之间的黏结力较小，空隙率增大，从而降低了初裂应力.

2）极限拉应力

由图4、表4可知，极限拉应力随着纤维掺量的增大呈现先增大后减小的趋势，在纤维掺量为1.5%时达到最大.相较PE-0.25-0.5试件，纤维掺量为1%、1.5%、2%、2.5%时极限拉应力分别提高了20%、44%、31%、22%.可能是纤维体积掺量较小时，纤维桥接能力不足导致极限拉应力增加较少，当纤维体积掺量较大时，纤维在基体中分布不均，导致不能发挥全部的桥接作用.极限拉应力随着水胶比的增大而减小.相较PE-0.25-1.5试件，水胶比为0.28、0.31、0.34时极限拉应力分别减少了19%、20%、32%.试件抗拉强度主要取决于纤维的桥接作用，PE纤维抗拉强度较高，在试件拉伸破坏中多为拔出破坏，PE纤维属于憎水性材料，与基体之间无化学黏结力[4].随着水胶比的增加，纤维与基体之间的摩擦黏结力较弱，阻裂效果不明显，极限拉应力随之减小.

3）极限拉应变

由图5、表4可知，随着纤维掺量的增大，极限拉应变先增大后减小，在纤维掺量为1.5%时达到最大.相较PE-0.25-0.5试件，纤维掺量为1%、1.5%、2%、2.5%时极限拉应变分别提高了31%、140%、72%、49%.结果表明：掺入纤维可以增大试件的极限拉应变.其中纤维掺量为1.5%时增加的最多，说明1.5%掺量可以使纤维在基体中均匀分布，充分发挥纤维的桥接作用，进而提高极限拉应变.随着水胶比的增大，极限拉应变先减小后增大.相较PE-0.25-1.5试件，水胶比为0.28、0.31、0.34时极限拉应变分别减少了34%、26%、19%.随着水胶比的降低，纤维与基体之间的摩擦黏结力变弱，但是纤维在基体中的分布更均匀，使得试件的延性增加.

图5 水胶比及纤维掺量对极限拉应变的影响

4）拉伸韧性

PE-ECC的拉伸变形性能可以通过韧性指数进行评价，拉伸韧性指数为应力-应变曲线包围的面积[11].由图6、表4可知，PE-0.25-1.5试件的拉伸韧性指数最大.水胶比增大有利于纤维在基体中的分布，但对纤维与基体之间的摩擦黏结力有影响；纤维掺量的增大有利于增加纤维的桥接作用，但不利于纤维在基体中的分布.当纤维掺量为1.5%、水胶比为0.25时，PE-ECC试件的拉伸性能达到最佳.

图6 水胶比及纤维掺量对拉伸韧性指数的影响

3 本构模型

3.1 PE-ECC受拉应力-应变关系分析

由图2可知，沙漠砂PE-ECC的破坏模式呈现三阶段特征：1）线弹性阶段.此阶段基体为受力主体，纤维由于物理性质在试件初期并不承担拉力，试件表面无裂缝产生.2）强化阶段.此阶段PE纤维与基体共同受力，随着荷载的增加，基体产生裂缝，此时裂缝间的纤维承担拉力，抑制裂缝扩展与延伸，并将应力传递到周围未开裂的基体上，将应力重分布，图中表现为波动上升.3）破坏阶段.纤维承担主要拉力，此阶段多条细密裂缝逐渐相汇，形成一条主裂缝，随着裂缝宽度的不断增大，裂缝间的纤维被拔出从而失去作用，当裂缝宽度达到一定值时，试件破坏.

3.2 模型建立

ECC材料发展至今，其拉伸本构关系可以分为双线模型和三线模型，其中双线模型较为普遍.双线模型将极限拉应力定义为临界点，超过极限拉应力则视为破坏，并在此处取极限拉应变.通过线性回归或理论计算的方法将强化阶段定义为线性关系来近似反映应力-应变关系.由图7（b）可知，沙漠砂PE-ECC试件的极限拉应力与极限拉应变并不在同一个点，故该双线模型不适用沙漠砂PE-ECC的单轴拉伸试验曲线；若将该模型用于预测沙漠砂PE-ECC的应力-应变曲线，将极限拉应力对应的点作为试件破坏点，则后半段的曲线作为软化段会被忽略，造成承载力过剩的问题.

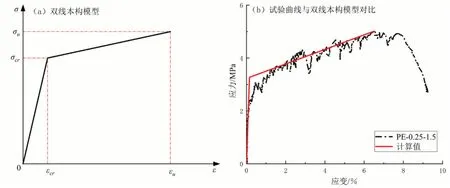
图7 双线本构模型和试验曲线与双线本构模型对比

三线模型则在上述基础上考虑极限拉应力与极限拉应变不在同一位置，并增加软化阶段，防止承载力过剩；传统的三线模型将强化段近似表现为线性关系，如图8所示，但与本文试验结果误差较大.

图8 三线本构模型和试验曲线与三线本构模型对比

综上所述，本文通过对PE-ECC进行单轴拉伸试验，并结合相关学者已发表研究成果[5-13]，为了更加准确描述强化阶段应力-应变关系使其更加贴近试验值，将强化阶段使用非线性曲线表示，见式（1）：

式中：σcr、σu、σc分别表示PE-ECC的初裂应力、极限拉应力、极限拉应变所对应的抗拉强度；E为弹性模量；A为强化系数，t为修正系数，D为软化系数；εcr、εu、εc分别表示PE-ECC的初裂应变、极限拉应变、极限拉应力所对应的拉应变.

3.3 模型参数定义

试验过程中夹具夹紧试件时可能会造成加载方向不在试件中心轴线上，使得所测初裂荷载值偏小.故将弹性阶段与强化阶段拟合所得的交点定义为名义初裂点[16].将弹性阶段定义为线性关系，即弹性阶段斜率为沙漠砂PE-ECC弹性模量E，弹性阶段的应力-应变关系用式（2）表示：

试件在弹性阶段过后，于最大初始缺陷处开裂，试件开裂后由纤维承担抗拉应力.随应力逐渐增大，缺陷较小处开始开裂，开裂处纤维继续承担抗拉应力，过程反复直至裂缝贯穿试件，试件破坏.由于沙漠砂的掺入，改变了基体的材料组成，影响纤维在基体中的分布及纤维与基体之间、基体颗粒之间的摩擦黏结力，导致试件在应变硬化阶段呈现出应力增长逐渐减缓的趋势.

将强化阶段定义为非线性关系，引入强化系数A，表示纤维掺量及水胶比对PE-ECC抗拉强度的增强幅度；同时引入修正系数t，表示ECC掺有沙漠砂后，沙漠砂对PE-ECC抗拉强度影响的修正.强化阶段的应力-应变关系用式（3）表示：

将软化阶段应力-应变关系简化为线性关系，引入软化系数D，表示PE-ECC试件达到极限应力之后，PE纤维在基体中桥接应力的衰减趋势.通过试验可知，PE-ECC试件在达到极限拉应力之后，下降趋势缓慢，仍有较高的承载力，呈现多裂缝开展行为，软化阶段的应力-应变关系用式（4）表示：

使用最小二乘法对试验数据进行回归分析，得到强化系数A、修正系数t、软化系数D，结果如表5所示.由表5可知，纤维掺量及水胶比不同对PE-ECC拉伸性能的影响不同.t值越大，表明沙漠砂对PE-ECC抗拉性能的影响越小；A值越大，表明纤维及水胶比对PEECC抗拉性能的增幅越明显；软化阶段D值越小，应力下降得越慢.对于PE-ECC，在纤维掺量为1.5%、水胶比为0.25时抗拉性能最好，沙漠砂在基体中发挥优势明显.本研究中t值随着水胶比的增大而减小，随着纤维体积掺量的增大呈现先增大后减小的趋势，而纤维掺量为2.0%相较2.5%的t值减小，可能是纤维基体中的分布具有离散型.A值随着水胶比的增大而增大，随着纤维掺量的增大呈现先减小后增大的趋势.由于水胶比过大严重影响了基体颗粒之间、基体与纤维之间的摩擦黏结力，导致初裂应力及极限拉应力均变小，当水胶比为0.34时，试件的初裂应力与极限拉应力相较水胶比为0.25、0.28、0.31时减小，与前期试验结果一致.

表5 相关参数

3.4 模型验证

为了验证本文所提PE-ECC单轴拉伸本构模型的准确性，以水胶比为0.25和纤维掺量为1%、1.5%、2%重新制作PE-ECC哑铃型试件进行单轴拉伸试验.将PE-ECC单轴拉伸本构模型与试验曲线进行对比（图9），验证PEECC单轴拉伸本构模型的准确性；使用本构模型计算结果与试验值进行对比分析，具体结果如表6所示.由图9、表6可知，计算所得的应力-应变曲线与试验曲线较为吻合，得出变异系数分别为0.064、0.052、0.035，说明计算值与试验值离散程度较小.本文提出的PE-ECC拉伸本构模型可以较好地预测沙漠砂PE-ECC的拉伸应力-应变关系.

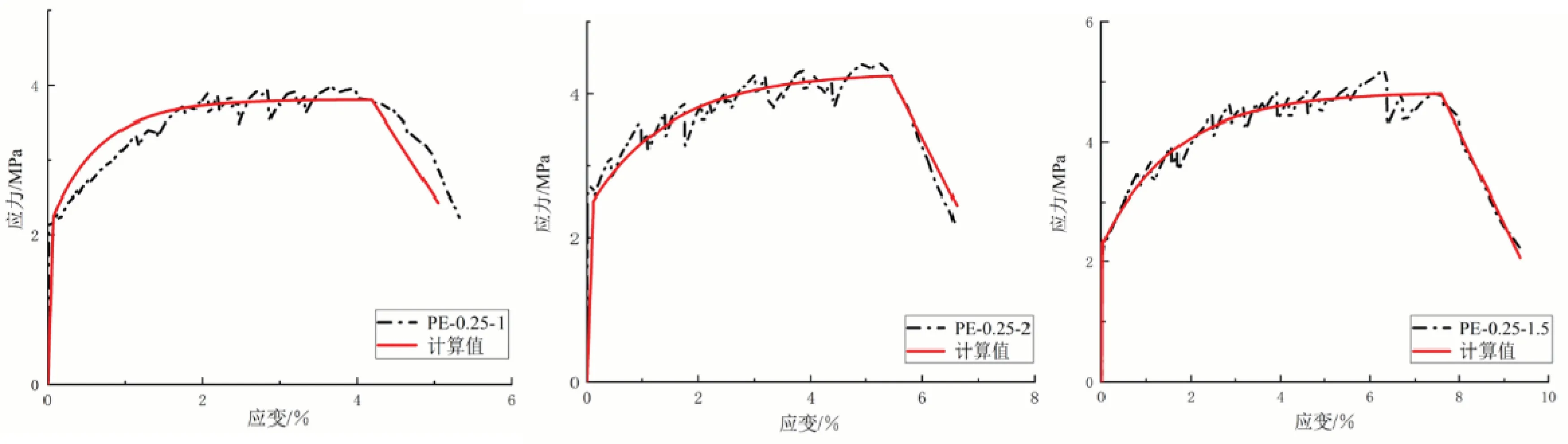
图9 PE-ECC受拉本构模型计算结果与试验曲线对比

表6 沙漠砂PE-ECC计算值与试验值对比

4 结论

1）随着纤维体积掺量的增加，沙漠砂PE-ECC的抗拉性能呈现先升高后降低的趋势.纤维体积掺量的增加可以提高纤维的桥接作用，但是纤维体积掺量过多则会影响纤维在基体中的分布.当纤维体积掺量为1.5%时，极限拉应力、极限拉应变与拉伸韧性均达到最大值.

2）由于水胶比会影响纤维与基体之间的摩擦黏结力，故随着水胶比的增大，沙漠砂PE-ECC试件的初裂应力、极限拉应力以及极限拉应变均有所降低，降低幅度为8%～34%.在水胶比为0.25、纤维体积掺量为1.5%时，沙漠砂PE-ECC试件拉伸性能最好.

3）本文提出的沙漠砂PE-ECC拉伸本构模型的强化阶段使用非线性曲线表示，通过模型计算结果与试验结果的对比分析，该拉伸本构模型可以较好地预测沙漠砂PE-ECC的拉伸应力-应变关系.由于不同的纤维对其拉伸性能的影响不同，所建本构模型仅考虑了PE纤维对沙漠砂PE-ECC拉伸性能的预测.