基于去噪扩散概率模型的InSAR相位解缠

刘明泰,岳东杰

(河海大学,江苏 南京 210098)

0 引 言

近些年来相位图像在各个领域得到广泛应用,如干涉合成孔径雷达InSAR,磁共振成像 MRI以及激光雷达等相位成像技术,然而它们在应用过程中都面临一个共同的问题——相位解缠。传统相位解缠算法包括路径跟踪法(枝切法[1]、质量图引导法[2]、最小不连续法[3])、最小范数法 (最小二乘法[4])、基于网络流的优化方法(最小费用流法[5-6])等,都难以在噪声和形变较大的区域恢复出真实的地形和形变相位。随着深度学习模型的发展,在图像处理领域提出了越来越多的模型如CNN、RNN、GAN、 Transformer等,这些模型也被用于InSAR的相位解缠研究。Spoorthietal等[7]认为相位解缠是一个语义分割问题,即预测每个像素的缠绕数量(整数为2π),然后将其添加到缠绕相位中以获得最终解,通过卷积神经网络CNN构建PhaseNet模型来求解缠绕整周数,恢复展开相位。Zhou Lifan等[8]将GAN 用于相位解缠,将解缠视作图像到图像的转换问题,通过对抗学习来训练相位解缠模型 PUGAN。Wu Zhipeng等[9]提出了适用于矿区快速挖掘引起快速变形的解缠网络 PUNet[9-10]。近几年随着扩散模型DDPM[11]的提出,其在AI绘画领域取得了许多令人惊叹的研究成果,如stableDiffusion、NovelAI、Waifu 等。这些成果无不论证了扩散模型的潜力。基于此本文将扩散生成模型引入相位解缠领域,并与传统相位解缠算法、基于深度学习的解缠模型进行比较,从而评价模型的解缠能力。

1 扩散概率模型DDPM

(1)

图1 干涉相位图扩散过程

(2)

(3)

给定足够的T和表现良好的噪声表βt,最终时刻的潜在变量xt几乎是各相同性的高斯分布。因此,如果知道确切的反向分布q(xt-1|xt),就可以对xt～N(0,1)进行采样,并反向运行该过程,最终从q(x0)中获得结果。上述反向运算的过程称为逆扩散过程,由于逆向分布q(xt-1|xt)取决于整个数据分布,因此可使用神经网络来拟合每步的逆向分布,如公式(4)所示。

Pθ(xt-1|xt)=N[xt-1;uθ(xt,t),∑θ(xt,t)]

(4)

扩散模型通过优化目标函数的下界(ELBO)来最小化负对数似然函数,可以将变分下界写为:

LELBO=L0+L1+...+Lt

(5)

L0=-logpθ(x0|x1)

(6)

Lt-1=Dkl[q(xt-1|xt,x0)||pθ(xt-1|xt)]

(7)

Lt=Dkl[q(xt|x0)||p(xt)]

(8)

除了常数L0,ELBO的每一项都是两个高斯分布之间的KL散度,其中Lt项并不依赖于神经网络中的参数θ,因此,可以只对Lt-1项进行化简,虽真实分布q(xt-1|xt)未知,但加上条件x0的后验分布q(xt-1|xt,x0)可以通过贝叶斯公式得到公式(8),最终优化目标函数的下界写作各个步骤t的后验高斯分布与神经网络拟合的高斯分布之间的KL散度,如下所示。

(9)

为了便于计算,Ho等[11]将网络拟合的分布P的方差设为常数,根据高斯分布之间的KL散度公式,后验分布q(xt-1|xt,x0)与网络拟合的分布Pθ(xt-1|xt)之间的KL散度可以写作公式(11),并且使用网络去预测均值uθ(xt,t)的效果不如预测噪音ε的效果好,噪音ε与均值uθ的关系如下所示。

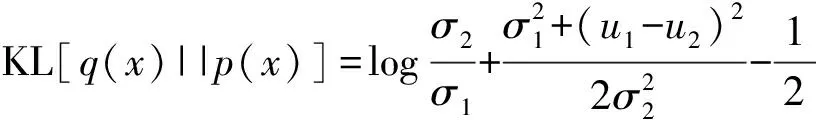
(10)

(11)

(12)

Lsimple=Et,x0{[ε-εθ(xt-t)]2}

(13)

2 实验数据以及训练、推理流程

在有噪声且快速变形的干涉图中,可靠的相位解缠是困难的,采集足够的地面测量数据进行训练是不可行的。因此,需要生成与真实干涉图特征接近的合成干涉图,并将其用于训练。干涉图的相位可以分解为地形相位、形变相位、大气湍流相位和噪声。本文采用了两种方法来获取干涉图数据,一种是构建干涉图模拟器,通过干涉图模拟器来模拟生成干涉相位图数据,另一种为使用LiCSAR系统自动处理生成的Sentinel-1干涉图数据,训练样本大小设置为256×256像素,覆盖面积约为5 km×5 km,小样本可以加快训练过程。

2.1 LiCSAR数据

LiCSAR的干涉图产品包括干涉图、相干图、解缠图,LiCSAR干涉图的数据以Frame为单位(250 km×250 km),提供tif和png格式的数据,空间分辨率110 m,为短时间基线干涉图(每张影像与其后续3张影像进行干涉),如图2所示。由于训练网络所需要数据的像素大小为256×256,因此要对下载得到的数据进行预处理,对数据进行旋转和裁切,如图3所示。

图2 LiCSAR数据

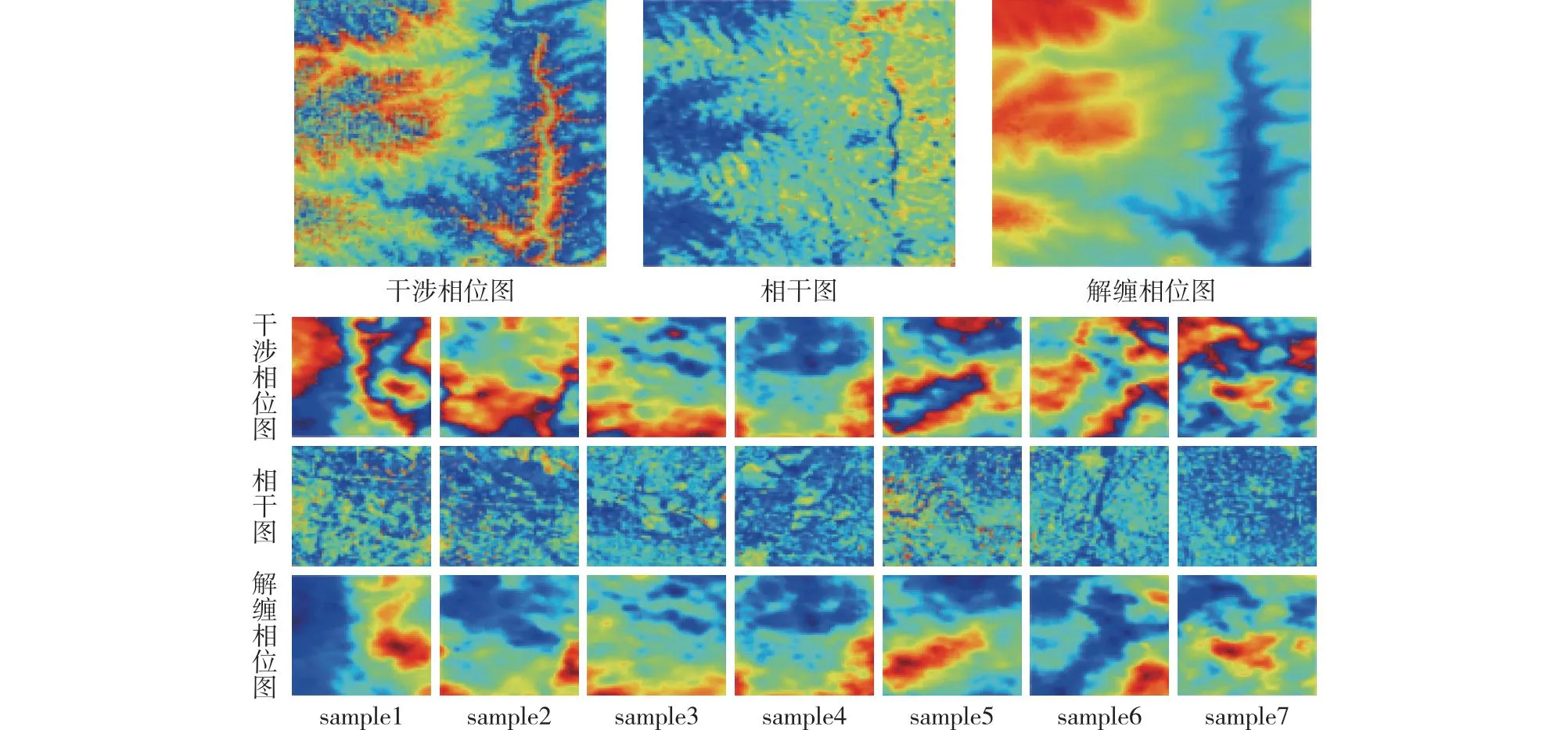
图3 预处理后的LiCSAR

2.2 干涉图模拟器

干涉图模拟器通过输入随机裁剪256×256像素的DEM地形数据用于生成地形相位图4(a)。除此之外,使用二维高斯曲面和5×5的随机向量生成二维扭曲高斯曲面来模拟形变相位图4(b),而大气相位图4(c)可以使用分形柏林噪声进行模拟。最后,考虑到噪声相位的影响,可以通过添加高斯噪声进行模拟。从而生成绝对相位图4(d)并进行相位缠绕运算,得到干涉相位图4(e),其流程如图4所示。

图4 模拟干涉相位图

2.3 训练推理流程

基于去噪概率扩散的相位解缠模型在训练过程中,根据真实相位x0以及t时刻随机采样的噪声值εt来获得扩散过程中t时刻经过加噪后的值xt,将xt和缠绕相位以及t时刻输入网络中得到预测的噪声εθ,t,根据公式(13),计算εt和εθ,t的均方误差MSE,来反向梯度传播优化网络。在推理过程中,将缠绕相位和随机采样的噪声值xt以及最终时刻T输入网络,获得T-1时刻的采样值xT-1,之后将缠绕相位和xT-1以及T-1时刻输入网络获得上一时刻的值。就这样逐步采样,最终获得预测的真实相位,其训练和推理流程如图5和表1所示。

表1 训练和推理流程

图5 训练和推理流程

3 实验结果及分析

3.1 评测指标

由于相位解缠的结果是绝对相位中各像素之间的相对值,其结果并非唯一解(即解缠相位与真实相位相差一个常数,其解缠结果依然能准确反映出地形的起伏变化),采用原始相位和解缠相位之间的均方误差并不能很好反映解缠结果的精度,因此本文采用原始相位和解缠相位之间差值的方差作为评测的L1指标,采用原始相位的相位梯度和解缠相位的相位梯度作为评测的L2指标:

L1=E[(Ψ-Ψθ)2]-E2(Ψ-Ψθ)

(14)

(15)

Gver=Ψi,j+1-Ψi,j

(16)

Ghor=Ψi+1,j-Ψi,j

(17)

3.2 不同相位解缠方法的结果比较

在相位解缠领域,有许多不同的方法可用于解缠干涉相位。在本文的实验中,将本文提出的基于去噪扩散概率模型的相位解缠模型与4种传统的相位解缠方法,包括枝切法、质量图引导法、最小二乘法、最小费用流相位解缠方法以及3种深度学习相位解缠模型PhaseNet2.0、PUNet、PU-GAN进行比较。本实验采样用3 000个样本对这些方法进行了测试,并对解缠结果进行比较和分析,其中3 000幅干涉相位图样本组成的测试数据集在L1指标下的误差分布如图6所示,在L2指标下的误差分布如图7所示。

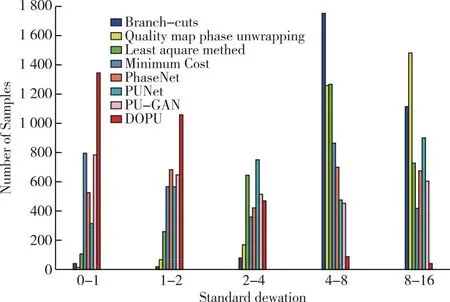
图6 数据集上在L1指标的相位展开误差分布

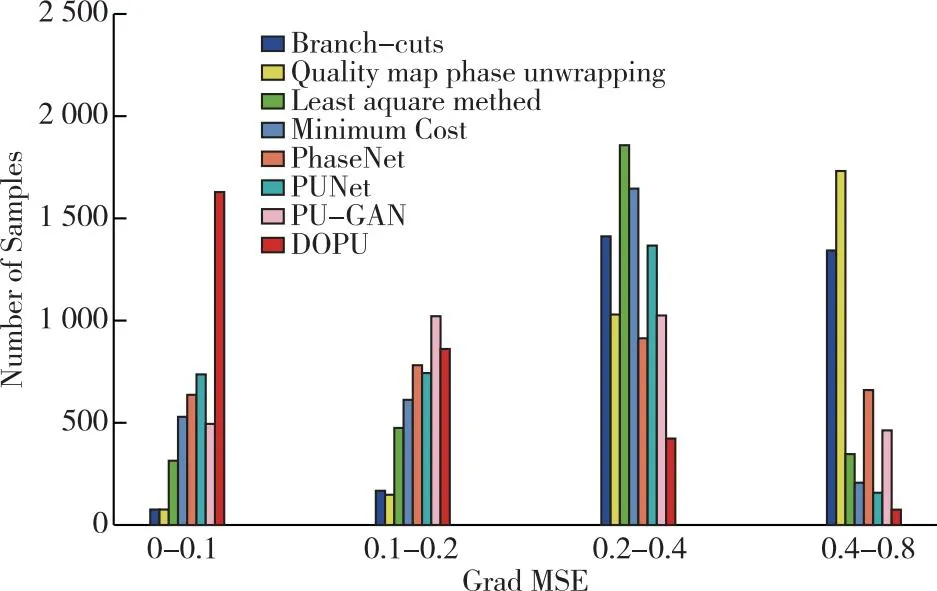
图7 数据集上在L2指标的相位展开误差分布

结果表明,DDPU的解缠结果在L1指标下,测试样本的误差σ多分布于0～2的区间内,|σ|<2的样本占86.53%,相比之下传统相位解缠算法中的枝切法和质量图引导法在不同信噪比的样本测试中,噪声的影响导致效果十分不理想,解缠结果的误差大多分布于4～16的区间,最小二乘法的效果表现一般,解缠效果优于枝切法和质量图引导法,较差于最小费用流方法,其解缠结果的误差多分布于2～8的区间内。最小费用流的相位解缠方法是4种传统相位解缠算法中表现最好的算法,在一些情况下甚至优于个别基于深度学习的相位解缠算法。在深度学习相位解缠算法中,DDPU的解缠效果要明显优于PUNet、PhaseNet和PU-GAN,DDPU通过抑制大偏差的发生,显著提高了展开干涉图的可靠性。

在L2指标下,测试样本的解缠相位梯度和原始相位梯度之间的均方误差多分布于0～0.1和0.1～0.2的区间内,占比83.2%。根据上述结果,可以看出使用对抗生成模型的PU-GAN解缠所得的数据较为平滑,不会出现较大的误差,因此其解缠结果的相位梯度多分布于中间值0.1～0.4的区间内,基于扩散概率的相位解缠模型DDPU不仅在整体上能更好符合原始相位,在梯度变化处也能更好地恢复出原始相位即大多数样本处于0～0.1这个低误差区间内。

根据3 000个样本在指标L1和指标L2下8种方法的解缠结果误差以及最大值和最小值,绘制箱型图来分析各个方法的鲁棒性,如图8所示。

图8 数据集上在L1指标L2指标的误差箱型图

由图8可知,DDPU方法所得到的解缠误差分布相对于其他方法来说更加紧凑,即四分位距(上下四分位之差)更小。这表明DDPU方法在不同信噪比条件下具有更强的稳定性和鲁棒性,能够有效地抑制大误差的发生。相比之下,其他方法的解缠误差分布比较散乱,四分位距较大,说明这些方法在不同程度的噪声情况下容易出现大幅度的偏差,稳定性相对较差。因此,DDPU方法在实际应用中具有更高的可靠性和准确性,能够更好地满足解缠需求。而且,DDPU解缠误差的均值和中位数也小于其他解缠方法,这表明DDPU的解缠结果更加准确。

为了更加直观展示DDPU的解缠效果,采用三幅不同噪声水平的模拟干涉图,并进行了相位展开处理,其结果如图9所示,相位展开误差如图10所示。其中,样本2的噪声水平低,条纹清晰,使得以上各种方法都能取得较好的解缠结果,然而随着信噪比的下降即干涉相位中噪声水平的提高如样本1和样本3,传统方法中的枝切法、质量图引导法便很难获得正确的解缠结果,最小二乘法的解缠误差覆盖了整个干涉图,最小费用流和其他深度学习相位解缠算法在地形起伏大的区域均有一定幅度的解缠误差,而本文提出的DDPU模型相对于其他相位解缠方法可以克服噪声的影响,精确地从干涉图中恢复出解缠相位。

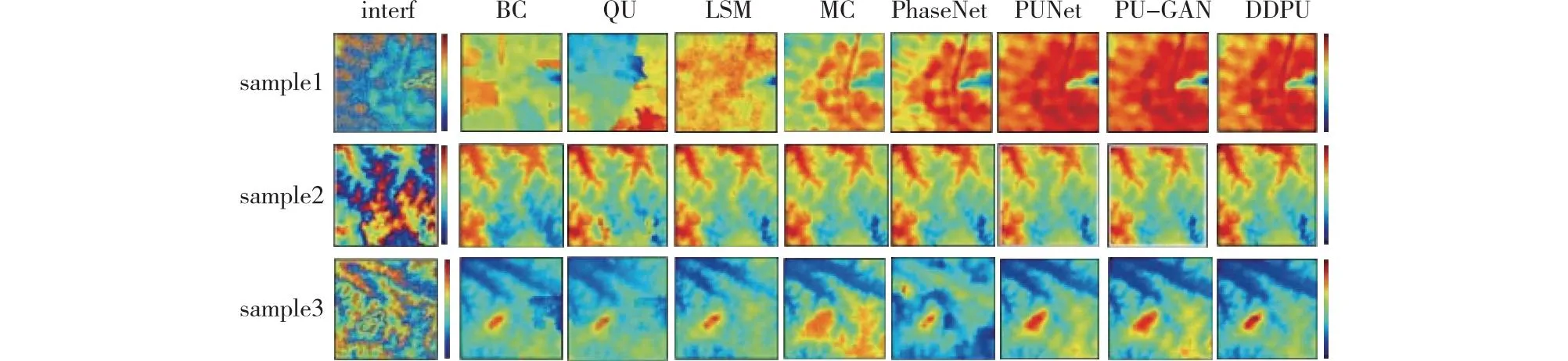
图9 不同噪声水平的干涉图实验结果

图10 不同方法解缠结果的误差

3.3 DDPU模型评估

为了评估DDPU相位解缠模型对于不同噪声水平和不同相位梯度干涉相位图的解缠效果,本文设计了一系列实验来对其进行全面的评测,旨在深入了解DDPU模型在不同噪声水平和相位梯度情况下的鲁棒性和性能表现,以验证其在实际应用中的可靠性和适用性。将不同噪声水平的测试样本传入DDPU模型中逐步获得解缠相位,使用评测指标L1对DDPU模型在不同噪声和相位梯度条件下的解缠效果进行定量评估和比较,其结果如图11所示。

图11 DDPU对不同噪声水平样本的解缠误差

结果表明,四组不同噪声水平的干涉图样本随着最大相位梯度的增大,起初,相位展开误差的标准差分布较为密集且都集中在较小的区域,之后随着最大相位梯度的增大,DDPU的解缠误差开始增大并且分布的更加离散。此外,DDPU表现出优秀的抗噪声能力,考虑到可接收的误差范围为小于1 rad,当噪声水平小于0.8π时,对于最大相位梯度小于4rad的干涉相位图,DDPU均能够获得良好的解缠结果。

4 结 语

将计算机视觉领域中的扩散生成模型引入相位解缠,通过与现有的几种相位解缠方法进行比较,发现扩散生成模型即使在严重的噪声条件下也能达到优秀的解缠性能,其对噪声的抵抗力非常适合于低信噪比的相位数据,且需要精确相位解缠结果的应用。展望未来,我们希望扩展该网络,以解决特定应用的挑战。