孔隙率对岩石力学性质和能量耗散影响的数值模拟*
严召松,梁 拯,黄义焕
(广东工商职业技术大学 建筑工程学院,广东 肇庆 526040)
岩石是一种天然地质体,在长期的地质作用下,其内部必然产生大量孔隙、裂隙,使得岩石具有不连续、非均质和各向异性的特征,这导致岩石的力学性质极为复杂。目前,已有部分专家对岩石不同孔隙率开展了相关的研究工作。例如:陆华等[1]利用SHPB冲击实验系统,开展2种孔隙率红砂岩的循环冲击试验,获得峰值应力、应变和变形模量随孔隙率的变化规律:孔隙率大的岩石抵抗冲击荷载的能力要弱于孔隙率小的岩石,并将岩石在循环荷载作用下的破坏过程归纳为孔隙闭合、裂隙开展、应力硬化和应变软化直至整体破坏四个阶段;肖巧林等[2]开展不同孔隙率玄武岩在干燥和饱水两种状态的单轴和三轴压缩力学试验,结果表明,岩石的抗压强度和弹性模量等力学参数随孔隙率增大呈指数递减规律;周巍等[3]将岩石的裂隙采用椭球形状的孔隙来模拟,改变椭球状的孔隙的纵向与横向尺寸比值,研究岩石的弹性、纵横波速等的变化规律,得出岩石的体积模量和弹性模量随孔隙纵向与横向尺寸比值增加而线性增大,泊松比呈非线性递减的规律;宋义敏等[4]开展红砂岩的单向压缩力学试验,分析岩石在荷载作用下的变形场和能量演化规律;李杨等[5]在研究孔隙率小于10%的岩石时,按照动能守恒原理和两相体的岩石模型,建立了弹性纵波波速与孔隙率之间关系的模型。
由此可见,孔隙率是影响岩石力学性质的一个较为重要的因素。本文基于岩石常规三轴压缩试验获取的基本力学参数,开展不同孔隙率岩石的数值模拟研究,探讨岩石的强度和变形,以及变形破坏过程中的能量演化规律,希望能对类似工程的开挖和支护设计提供一定的理论依据。
1 三轴压缩数值模拟
1.1 数值模型
采用直径为 25 mm、高度为 50 mm 的圆柱形试件模型。采用楔形网格,大小为 0.5 mm,对模型试件进行细化单元处理,共划分为417300个单元,如图1所示。通过ABAQUS运行python编程脚本,实现模型单元的随机删除,从而获得孔隙率分别为10%、20%、30%、40%的计算模型。

图1 数值模型
1.2 模型参数
本研究的计算模型单元采用的岩石弹性、 塑性力学参数由许江等[6]岩石渐进性破坏过程中变形和能量分析论文中围压 3 MPa 试验数据处理获得。 密度为2×10-3g/mm3,弹性模量E为 10.07 GPa,泊松比μ为0.25。 ABAQUS中超出弹性部分的受压应力应变曲线数据以δ-εp的形式输入。 计算公式如式(1)、 式(2)。
(1)
(2)
式中:ε为应变;σ为应力;E为弹性模量;εe为弹性应变;εp为塑性应变。
在轴向加载,设定恒定速率10-4/s加载[7],时间为 130 s,采用动力显示,质量缩放取108,围压为 3 MPa,底部单元轴向位移固定。
2 数值模拟结果
2.1 不同孔隙率岩石的应力、应变分析
主应力差在加载初期随轴向应变线性增加如图2所示。当应力超过起裂应力时,轴向应力呈非线性增长,且增长速率逐渐减小;到达峰值强度后,应力快速降低,形成明显应变局部化带。随着岩石中孔隙的增多,峰值强度之后,应力降低幅度减小,应变软化现象变得不明显。

图2 不同孔隙率岩石主应力差-轴向应变曲线
当孔隙率为10%时,在试件中下部形成一条明显的剪切应变局部化带,峰值应力之后,应力快速降低,发生脆性破坏;当孔隙率为20%、30%时,试件出现交汇于上端部的两条剪切破坏带;孔隙率为40%时,在试件的上、下端部出现较多的破坏带,峰值强度之后,应力缓慢降低,使得更多孔隙得以贯通,呈现延性破坏。如图3所示。
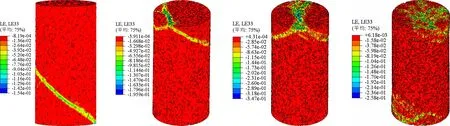
(a)10% (b)20% (c)30% (d)40%
由于孔隙增多,试件抵抗变形的能力减弱,孔隙间容易发生连通,故而试件的弹性模量E、峰值应力均线性降低,且线性相关性较好。如图4、图5所示。
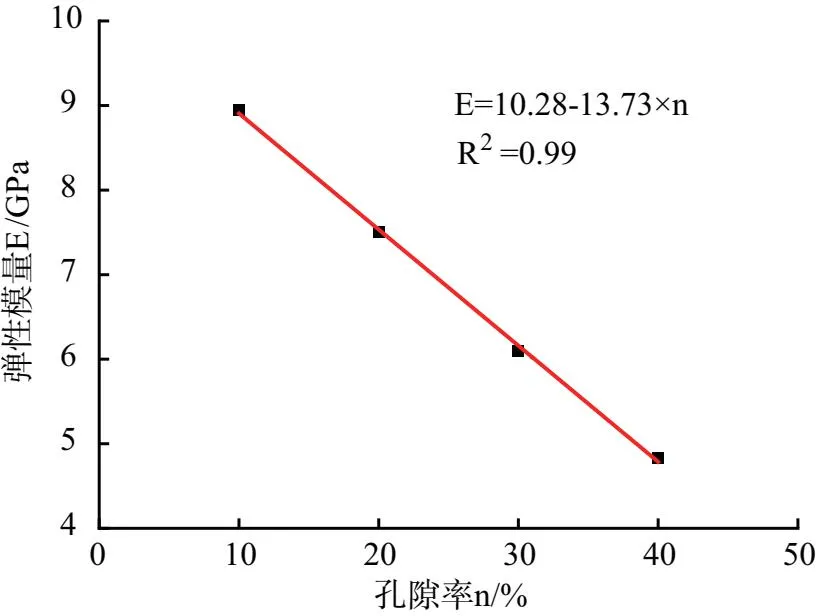
图4 岩石弹性模量-孔隙率曲线

图5 不同孔隙率条件下岩石的峰值应力
2.2 不同孔隙率条件下的能量分析
根据ABAQUS后处理提取能量输出数据,分析模型的内能Ei、弹性应变能Es、塑性耗散能Ep演化规律。
随着轴向应变的增加,内能缓慢增大,增加速率逐渐增加,曲线呈上凹;峰值应力之后,内能近似线性增加,这由于岩石发生破坏后将沿着破裂面发生滑移,输入的能量将主要用于克服破裂面间的摩擦作用而消耗。随着孔隙率的增加,试件的内能减小,且增加速率比较小,意味着使得岩石发生贯穿性裂纹破坏需要的能量比较小,孔隙多的岩石更加容易发生破坏。如图6所示。

图6 不同孔隙率条件下岩石的内能
峰值应力之前,岩石储存的弹性应变能随加载的进行逐渐增大,当达到峰值应力时,储存的弹性应变能最多;峰值应力之后,弹性应变能减小,一部分能量得以释放。
随着孔隙率的增大,岩石的弹性应变能增长速率减小;峰值强度之后弹性应变能释放量和释放速率均以随岩石中孔隙的增多而减小,孔隙率大的岩石弹性应变能缓慢释放,破坏过程较为缓慢,集中的应力得以充分转移,就使得更多的孔隙得以贯通,因而产生较多的裂纹,岩石呈现一定的延性破坏特性。如图7所示。

图7 不同孔隙率条件下岩石的弹性应变能
在加载初期,岩石在围压作用下较为致密,塑性耗散能接近于零;当应力达到一定值,孔隙开始扩展连通,产生塑性变形,塑性耗散能缓慢增加;在峰值应力附近塑性耗散能迅速增大,形成贯通裂纹之后,沿着破裂面产生滑移,此时塑性耗散能稳定增长。随着岩石中孔隙增多,岩石破坏不需要消耗过多的能量产生裂纹,故而耗散的能量及增长速率随孔隙率增大而减小。如图8所示。

图8 不同孔隙率条件下岩石的塑性耗散能
随着孔隙率的增加,峰值应力对应的内能、弹性应变能均线性减小,表示岩石中的孔隙越多,储存的弹性应变能越少,释放的能量越少,裂隙间相互贯通需要的内能少。如图9、图10所示。
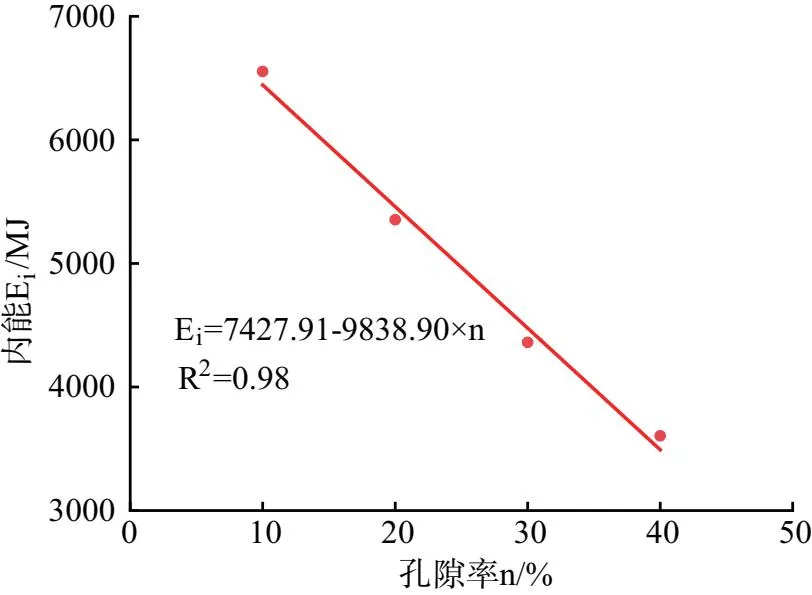
图9 岩石峰值应力对应的总应变能-孔隙率曲线
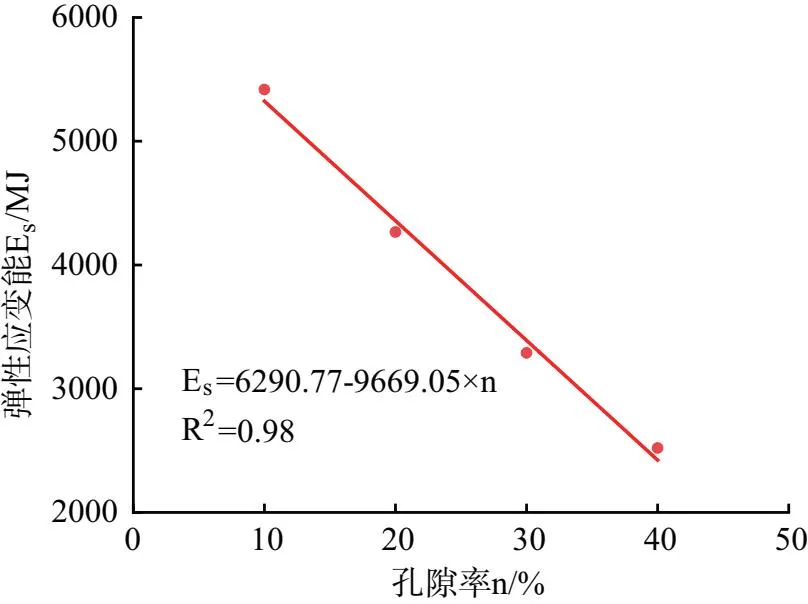
图10 岩石峰值应力对应的弹性应变能-孔隙率曲线
3 结论
1)随着孔隙率的增加,岩石抵抗变形的能力和强度减弱,弹性模量和峰值应力均呈线性减小;峰值应力之后,孔隙率越大,岩石应力的降低幅度越小,岩石由脆性破坏逐渐转为延性破坏。
2)在孔隙率较小时,岩石发生剪切破坏,形成一条明显的应变局部化带;随着孔隙率的增大,岩石出现多条交互的应变局部化带,使得岩石更加破碎。
3)在外载荷的作用下,岩石中的能量逐渐增多;随着孔隙率的增加,内能和储存的弹性应变能减小,峰值应力对应的内能和弹性应变能与孔隙率呈线性递减关系;峰值应力之后,内能稳定增加,弹性应变能则一部分释放,且随孔隙率的增加,释放量和释放速度均减小。
4)在加载初期,岩石发生弹性变形,此时塑性耗散能接近于零。当应力达到一定值时,塑性耗散能逐渐增大;在峰值应力附近,则快速增加,之后保持稳定增长。随着孔隙率的增大,峰值点附近的塑性耗散能增加幅度减小,峰值应力对应的塑性耗散能降低。

