基于5CV-Optuna-LightGBM回归模型的数据预测方法
顾靓 谈子楠 荣静

关键词:Pearson;五折交叉验证;Optuna;LightGBM;正则化
0 引言(Introduction)
机器学习模型相对于传统模型来说,其学习能力和泛化能力更强,占用的内存更低,训练速度更快而且效率也更高。随着机器学习的兴起,大量学者尝试建立相关的机器学习模型预测各种类型的数据,达到节约时间和经费的目的。与依赖于已知模式推导的线性回归等传统模型不同,机器学习模型不需要推导参数化详细的模型方程[1]。
本文以五折交叉验证、Optuna超参数优化和LightGBM回归预测模型为基础,建立LightGBM 混合模型,命名为5CVOptuna-LightGBM 回歸预测模型。为探讨5CV-Optuna-LightGBM回归预测模型的适用性,本文采用影响二手车价格的因素数据集对二手车价格进行预测。对比常用的5CVLightGBM回归预测模型和最优尺度回归模型,本文采用的5CV-Optuna-LightGBM回归预测模型占用的内存更低、预测值更加准确、建模效率更高及拟合度更高。
1 预备知识(Preliminary knowledge)
LightGBM 是一种机器学习算法,自2017年被首次提出以来,得到了广泛的研究和应用。KE等[2]提出了一种高效的基于决策树的梯度提升算法,采用多种优化技术提高了算法效率和泛化性能;SHEHADEH 等[3]建议使用修正决策树(MDT)、LightGBM 和XGBoost回归模型预测建筑设备的残值,提高了准确性并激发机器学习的潜力。除此之外,SRINIVAS等[4]利用优化的XGBoost分类器,使用超参数优化技术(OPTUNA)对超参数进行适当的调整,并使用五种指标评估系统的效率,证明该模型的预测结果更好。
1.1LightGBM 回归预测模型
1.1.1LightGBM 算法
LightGBM是一个实现梯度提升决策树(Gradient BoostingDecision Tree, GBDT)算法的框架[5],基于直方图的决策树算法,通过基于梯度的单边采样算法GOSS(Gradient-based One-Side Sampling)和互斥特征捆绑算法EFB(Exclusive FeatureBundling)改进,支持高效率并行训练,具有速度快、节省内存、泛化能力较好等优点[6]。直方图算法把连续的浮点特征值离散化成k 个整数,由此寻找最优切分点并取得最大增益,k 越小,其拟合准确度越低。利用直方图可以进行差分加速提高运算速度。在此基础上,LightGBM 使用按叶生长(Leaf-Wise)的算法[7]降低了模型损失。此外,LightGBM 需要设置一个决策树的最大深度用于分裂增益最大的结点,避免分裂的次数增加而发生过拟合的情况。在优化改进中,LightGBM 采用GOSS算法保留大梯度样本,对小梯度样本随机采样,减少训练误差;采用EFB算法将互斥特征进行合并,降低特征维度。
LightGBM中最重要的是模型训练。模型训练主要通过以下几个步骤进行参数设置[8]。(1)数据收集:收集影响二手车价格的因素数据;(2)特征工程:寻找能最大限度地反映因变量本质的自变量分类原始数据;(3)模型训练:不断训练数据,只有达到规定的迭代次数或者迭代过程,收敛才能停止;(4)交叉验证和模型评估:待LightGBM 模型达到最优后,通过模型评测对样本集和测试集进行模型检验,观察预测结果是否符合真实值。若数据不符合,则重新分类原始数据,重复上述步骤直到得出预期结果。
1.1.2L1正则化
LightGBM 在每次迭代时,会根据结果对样本进行权重调整,随着迭代次数的增加,模型偏差不断降低,导致模型对噪声越来越敏感。L1正则项将回归模型(regression_L1)作为目标函数(objective),通过参数稀疏化进行特征选择、降低噪声。随着正则项不断增大,相应变量系数不断缩减,直至为0。剔除零值特征,减少LightGBM 预测误差,损失函数达到全局最小值。损失函数L 的计算公式如下:
其中,L1正则项为μ‖w‖1,即权重向量中各元素的绝对值之和。在L1正则项回归模型中,μ 直接决定进入模型的变量个数,影响模型回归的准确性。
1.2 五折交叉验证
模型应用于验证数据中的评估常用的是交叉验证,又称循环验证[9]。特征交叉通过合成特征在多维特征数据集上进行非线性特征拟合,从而提高模型的准确性,防止过拟合。原始数据分成k 组不相交的子集,每个子集数据抽出m 个训练样例。在训练样例中随机抽取1组子集作为一次验证集,剩下的k-1组子集数据作为训练集,每组子集都经过一次验证,得到k 个模型。
假设数据集有特征x1 和x2,那么引入交叉特征值x3,使x3=x1x2,最终表达式如下:
1.3 Optuna超参数自动优化
Optuna是一种自动化软件框架,能对模型超参数进行优化[10]。Optuna可以通过选择多种优化方式确定最佳超参数,例如网格搜索、随机搜索和贝叶斯优化等。在Optuna的优化程序中,三个核心的概念分别为目标函数(objective)、单次试验(trial)和研究(study)。在机器学习中,为了找到最优的模型参数,研究人员需要定义一个待优化的函数objective,这个函数的输入是模型参数(也就是参/超参数),输出是针对这些模型参数的模型效果评估指标。对于每组参数,研究人员需要进行一次trial,通过贝叶斯优化或网格搜索等优化算法,探索参/超参数的范围。优化算法需要study对象进行管理和控制试验的次数、参数的探索范围等并记录下来,从而确定最优的模型参数组合。在优化过程中,Optuna利用修剪算法删除对分类作用小的过程,并通过反复调用和评估不同参数值的目标函数降低过拟合概率,获得最优解,降低误差。
2 数据处理(Data processing)
本文实验选取影响二手车价格的因素数据集,数据集样本共有30 000个。为方便处理数据,需要进行如下操作:提取tradeTime、registerDate、licenseDate等日期指标的年月日数值;anonymousFeature11数据表现为1+2、2+3等六种字符串,按顺序用数字1~6对这六种字符串数据进行标签编码。对其他数据按照本文2.1至2.4章节的步骤进行处理。
2.1 填补缺失值
条形密度图(图1)显示主要特征的缺失率,图中的空白越多,代表缺失的数据越多。部分二手车价格数据变量缺失率高于80%,直接去除會造成数据的严重浪费等问题。对高于80%的部分特征,如匿名特征(anonymousFeature4)等,则直接删除;余下的缺失率低于80%的部分特征,如cityid(车辆所在城市id)等,根据样本之间的相似性进行众数填充[11]。
2.2 长尾特征处理
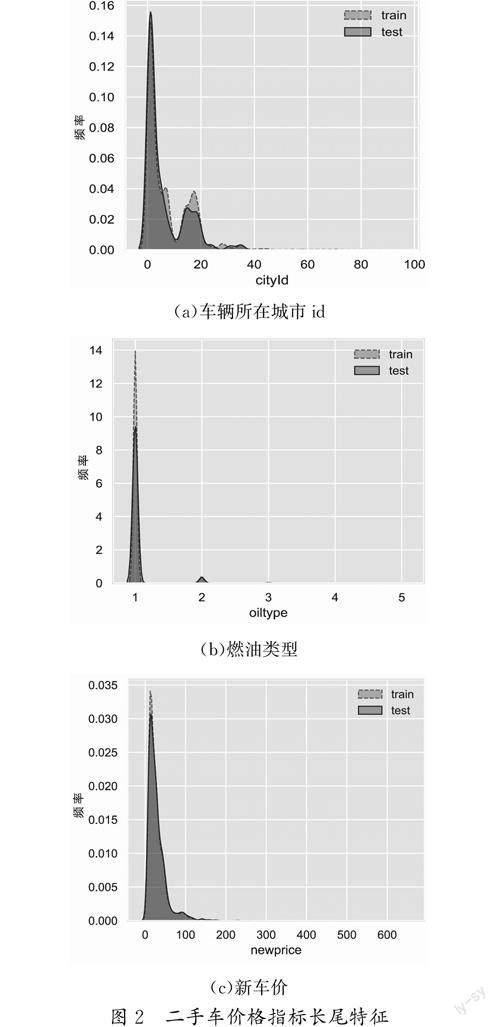
长尾是指某个或某几个连续变量的数值分布差别很大,呈现长尾图样式(图2)
对数变换的目标是帮助稳定方差,始终保持数据分布接近于正态分布,使得数据与分布的平均值无关。通过对数变换对cityid(车辆所在城市id)、oiltype(燃油类型)、newprice(新车价)等长尾特征进行处理[12]。
2.3 去除异常值
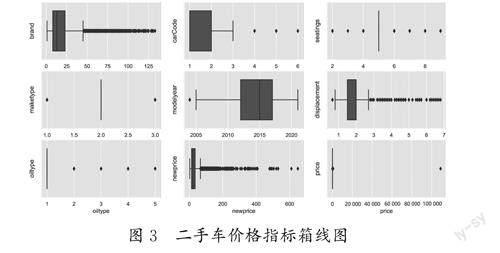
为了确保后续预测结果的准确性,训练数据必须符合实际情况。通过matplotlib(2D绘图库)的箱线图(图3)分析指标,去除数值大于或小于其整体数值(超出箱线图边距)的异常变量中的数据。
2.4 相关性分析
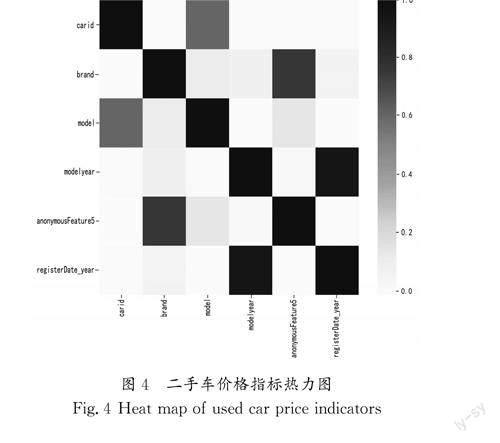
通过Pearson相关系数对时间特征进行相关性分析。Pearson相关系数是描述两个定距变量间联系的紧密程度和线性相关关系的参数[13]。通过Pearson相关系数可探求影响二手车价格变量之间的相关性,其计算公式如下:
其中:N 表示变量个数,x、y 表示变量的观测值。相关系数r的绝对值越大,其相关性越强;当r∈(0,1]时,表示x 与y 呈正相关,当r∈[-1,0)时,表示x 与y 呈负相关,当r=0时,x与y 无线性关系。
通过公式(3)对指标进行相关性计算,得到二手车价格指标热力图(图4),可知carid(车辆id)和model、brand(品牌id)和anonymousFeature5(匿名特征)、modelyear(年款)和registerDate_year(注册日期)等变量之间的相关系数均大于0.8,说明这些指标之间高度正相关,可以用其中一个指标代替其他指标[14]。
35CV-Optuna-LightGBM 回归预测模型(5CVOptuna-LightGBM regression prediction model)
为了提升预测结果的精度,本文在原始LightGBM 回归预测模型的基础上引入五折交叉验证和Optuna超参数自动优化,形成5CV-Optuna-LightGBM回归预测模型。
3.1 模型训练及参数优化
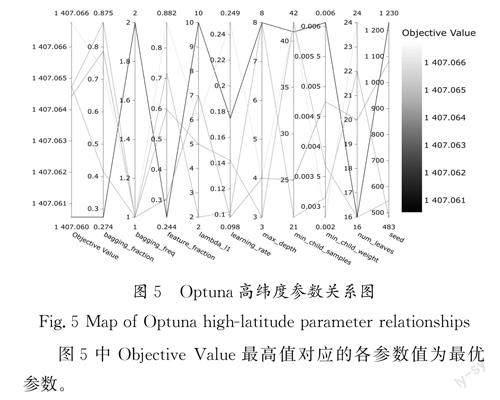
为提高LightGBM模型在默认参数下的诊断准确率,本文采用split方法将训练集和测试集划分为5份,每次迭代随机选取4份数据作为训练集,并对LighGBM模型中的10个特定超参数进行寻优,参数值在给定范围内随机生成,迭代1 000 000次。其中:参数num_leaves代表叶子节点数;参数max_depth代表树的深度,合适的树深度在一定程度上可以避免过拟合;参数feature_fraction代表子特征处理列采样;参数bagging_fraction代表建树的采样比例,具有泛化数据的能力;参数bagging_freq代表每k 次迭代进行子采样;参数learning_rate代表学习率,如果设定过小,会导致梯度下降很慢,而设定过大又会跨过最优值,产生振荡;参数min_child_weight代表叶子节点中样本数目;参数min_child_samples代表叶子节点最小记录数;参数seed代表指定随机种子数。Optuna高纬度参数关系图如图5所示。
3.2 交叉验证ROC 曲线
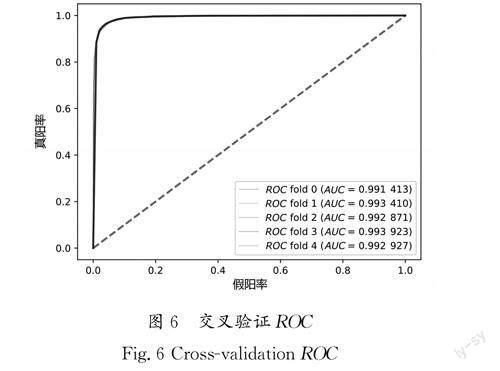
将训练集中price指标中低于10万元的标为0,高于10万元的标为1,利用受试者工作特征曲线ROC (ReceiverOperating Characteristic)判断交叉验证拟合度。其中,真阳性率(所有实际为阳性的样本被正确地判断为阳性的个数与所有实际为阳性的样本个数之比)为纵坐标,假阳性率(所有实际为阴性的样本被错误地判断为阳性的个数与所有实际为阴性的样本个数之比)为横坐标绘制的曲线,曲线越靠近左上方,则代表拟合程度越高。同时,二手车样本的检测数据变化较大,使用ROC 曲线可以使数据分析更加稳定,交叉验证ROC 如图6所示。
通过ROC 曲线分析,表明交叉验证下ROC 均大于0.99,模型性能优良。
3.3 评价指标
本文所采用的模型评价指标有平均绝对百分误差(MAPE)、对称平均绝对百分误差(SMAPE)、平均绝对值误差(MAE)、均方误差(MSE)、均方根误差(RMSE)和准确率(Accuracy),代表对样本的整体预测的准确程度,其中真实值y=(y1,y2,…,ym ),模型预测为^y=(^y1,^y2,…,^ym ),其计算公式分别如下:
Accuracy 采用相对误差在5%以内[count(Ape≤0.05)]的样本数量,其中Ape 为相对误差。
3.4 模型性能对比
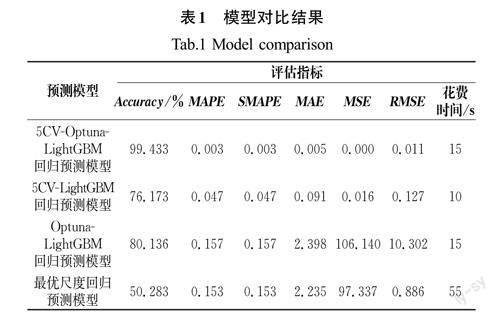
利用公式(4)至公式(9)分别求出5CV-Optuna-LightGBM回归预测模型、5CV-LightGBM 回归预测模型、Optuna-LightGBM回归预测模型和最优尺度回归预测模型的评价指标,并进行模型对比,模型对比结果如表1所示。
对比四个模型的准确率、平均决定值误差等误差指标和花费时间可以看出(表1),5CV-Optuna-LighGBM 回归预测模型的准确率最高,达到了99.433%。在预测值和实际值之间的差距方面,5CV-Optuna-LighGBM回归预测模型的MAE 等误差指标最小,预测最准确。在建模效率方面,5CV-Optuna-LightGBM回归预测模型花费的时间最少、效率最高。
4 预测结果(Predicted results
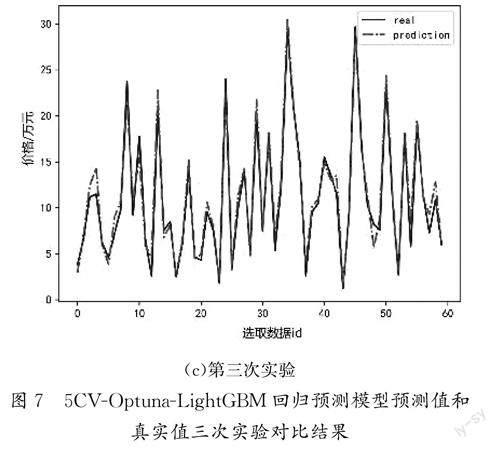
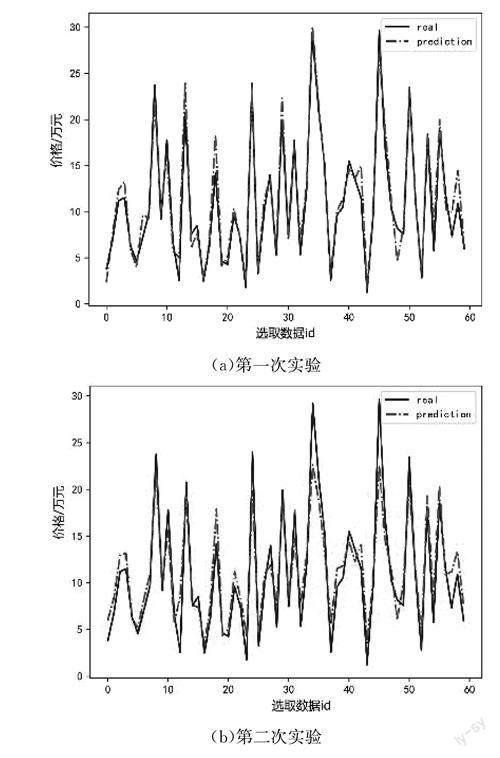
对二手车价格的预测值和真实值进行三次实验,提高结果的可靠性和泛化性,5CV-Optuna-LightGBM 回归预测模型预测值和真实值三次实验对比结果如图7所示。对比二手车价格的预测值和真实值分析得到数据基本一致,进一步验证模型的准确性。
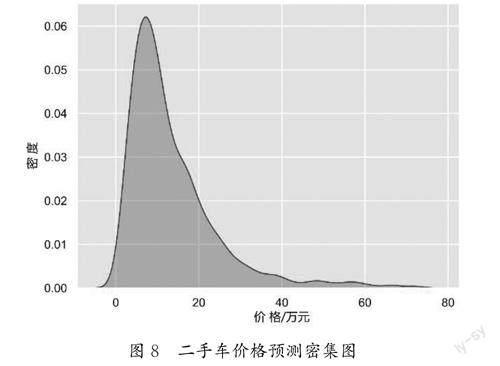
利用5CV-Optuna-LightGBM回归预测模型求出二手车价格预测结果,二手车价格预测密集图如图8所示。
图8中,预测价格在10万元左右的二手车成交频率最高,意味着大多数二手车的里程适中、座位数较少、车龄较老。通常,一些热门品牌和车型的二手车比较保价,而其他二手车的价格可能较低。10万元左右的二手车大多为中档车型或一些比较受欢迎的品牌,主要分布在二线和三线城市。此外,过户次数、车辆生产国家、排量等因素也在一定程度上影响二手车价格。
5 结论(Conclusion)
本文在影响二手车价格因素数据集上研究5CV-Optuna-LightGBM回归预测模型对于预测类问题的优势,并对该模型进行有效性检验。从实验结果来看,基于5CV-Optuna-LightGBM回归预测模型可将预测精度提高到99.433%,而预测时间降低到15 s,平均绝对值误差(MAE )、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分误差(MAPE)、对称平均绝对百分误差(SMAPE)分別减少到0.005、0.000、0.011、0.003、0.003,预测结果更准确。此模型可以在其他经济市场中为产品估价提供一定参考意见。
但是,本研究仍存在一些不足。数据处理解释了可能的误差来源,总体误差是可控的,但即使对几种方法的结果进行了比较,误差也依然存在。每种方法都有其优缺点,因此在不同的背景下,评估哪种方法是适宜的,具有一定的挑战性。此外,相关拟合方法仍有改进和完善的空间,可以添加拟合方法进行拟合度对比,获取更高的拟合度。今后,值得探索的一个领域是研究多组平行对照组。

