谷幅变形全天时自动化监测的精密气象改正方法

周 绿，张 凯，刘书明，杨泽发，肖亚子

(1.中国电建集团中南勘测设计研究院有限公司，湖南长沙410014；2.中南大学地球科学与信息物理学院，湖南长沙410083)

近些年来，我国一大批高拱坝投入建设运营，有效促进了社会经济发展。然而，在坝体运营过程中，尤其在蓄水期库区两岸山体受水位上升的影响，应力平衡状态易受扰动，从而形成大范围水平变形，简称“谷幅变形”[1-2]。数据显示，我国建成的高拱坝如溪洛渡水电站[3-4]、白鹤滩水电站[5]、锦屏一级水电站[6]等在正常蓄水过程中均监测到不同程度的谷幅变形。因此，准确监测高拱坝谷幅变形对保障水电站安全运营有重要意义。

目前，常用测量机器人等全自动化设备监测谷幅变形，其大都基于光电测距原理。然而，由于库区内气温、气压、湿度等因素变化复杂，其会对光电测距精度有显著影响。目前谷幅变形监测大都采用《中、短程光电测距规范》[7]推荐使用的经典气象改正模型提高监测精度。然而，该方法需假定观测时气象条件(比如气温、气压和湿度)相对平稳。因此，规范要求光电测距作业时间通常选取空气温度垂直变化梯度为零的前后1 h内(比如日出后0.5 h或日落前0.5 h)，而且在正午、雷雨、大雾、大风等复杂气象条件下气象模型精度较差。

随着我国水电站坝体高度和蓄水量的不断增加，对谷幅变形监测的精度和时间分辨率均提出了更高的要求(比如亚毫米精度、全天时监测等)。然而，受观测成本、天气条件等因素影响，人工谷幅变形监测不仅工作强度大，且时间分辨率也不高，难以满足水电站对于谷幅变形监测的时间分辨率要求。欲实现谷幅变形全天时自动监测，除仪器设备外，适用于全天时的测距气象改正方法显得尤为重要。目前，国内外学者在自动化气象改正方面开展了部分探索，并发展了邻边比例法、基线神经网络法、差分数据处理、似差分改正与模型改正等多种算法[8-10]，取得了一定效果。然而，这些方法大都需要以一条已知且长度不变的精确基线作为参考依据。由于水电站蓄水影响范围较大，且微气象学变化显著，因此，在谷幅观测线附近选取一条长度不变，且具有代表性的精确基线较为困难。

为此，本文通过充分挖掘谷幅变形自动化监测数据内部的演化趋势，通过引入现代测量平差理论发展一种谷幅变形全天时自动化监测精密气象改正方法。该方法首先采用传统气象改正模型对谷幅测距数据进行初步改正；随后，基于Fourier数进一步拟合并去除全天时测距趋势性偏差，并采用稳健Kalman滤波方法削弱随机误差；最后，基于非参数拟合的加权最小二乘方法计算全天时谷幅变形值。

1 研究方法

1.1 基于传统气象改正模型的谷幅测距初步改正

根据文献[7]，经典气象改正模型可表示为

dD≈(n0-n)D′=(N′g-N″g)×10-6×D′

(1)

式中，D′为待气象改正的原始测距值，m；N′g为仪器标称群折射率；N″g为实际作业大气条件下的群折射率；dD为气象修正值；n为测量时气象条件下的实际群折射率；n0为仪器气象参考点的群折射率。

Barrell和Sears所描述的标准大气条件(0 ℃，1 013.25 hPa，包含0.03%的二氧化碳的干燥空气)下可见光和近红外调制辐射的群折射率Ngo(标准大气)为

(2)

式中，电磁波波长为微米级时，A=287.604，B=1.628 8和C=0.013 6；λ为真空中光波的有效波长。代入计算得

(3)

波长在560～900 μm间，公式(3)的精度能精确到±0.1 ppm。为了适应测距时的实际大气条件，Barrell和Sears对公式做如下修改，为

(4)

式中，Ng为一般大气的群折射率，ppm；Ngo为标准大气的群折射率，ppm；T为绝对温度，K；P为大气压，hPa；e为水蒸气压力，hPa；Q为常数，取0.269 6；V为常数，取11.27。

由于湿度观测相对容易，因此，大多数谷幅变形自动化监测直接观测相对湿度h，与水蒸气压力e的关系式为

(5)

式中，E为饱和水蒸气压，可通过实测湿球温度tw(单位为℃)估计，即

(6)

1.2 基于Fourier级数的全天时测距趋势误差估计

通过分析传统大气改正后的距离值，发现其存在周期性系统性误差。出现该现象的原因可能是现有气象误差改正模型要求气象条件相对平稳，而该要求在全天时观测时难以准确满足导致的。由于本文采用加权最小二乘估计全天时谷幅变形，该方法要求观测数据仅含随机误差，因此，需对传统气象模型改正后的谷幅距离观测值进行趋势误差去除。考虑到Fourier级数具有较好的趋势项描述能力[11-12]，因此，本文采用该函数拟合并去除全天时测距趋势误差。

Fourier拟合算法可采用一对正交函数通过对Fourier级数的变换，不断逼近离散数据的平滑处理。通过Fourier级数拟合方法估计全天时谷幅距离值(经过传统气象模型校正之后)平均偏差误差趋势，发现其可用如下公式表示

(7)

式中，f(x)为周期的连续函数，周期为T；a0、ω为常系数；n为傅里叶展开级数；角频率ω=2π/T；ai、bi(1≤i≤n)为Fourier系数。

1.3 基于稳健Kalman滤波的全天时谷幅测距随机误差削弱

经过趋势项偏差去除之后，本文采用稳健Kalman滤波方法削弱全天时谷幅测距观测值的随机误差。Kalman滤波[13]算法可根据上一次的估计值与本次的测量值，结合二者的误差计算出的增益系数，从而计算本次的估计值，即

(8)

(9)

传统Kalman滤波算法是以可靠的函数模型和随机模型为前提，当其面对状态模型不准确或观测误差中含有粗差的场景时，其估计结果可能出现错误。为了克服该局限，本文采用稳健Kalman滤波算法[14]削弱谷幅测距的随机误差。稳健Kalman滤波算法将抗差理论与传统Kalman滤波方法结合，其重点在于权矩阵的设计。本文采用目前较为常用的IGG-I加权方案，即

(10)

(11)

式中，PXk为预报值的权矩阵，由其协方差矩阵DXk求逆获得。

1.4 联合非参数拟合与加权最小二乘的全天时谷幅变形监测

经过稳健Kalman滤波后，谷幅测距观测值的随机误差得到了较好的削弱。然而，此时的测距观测值精度可能仍难以满足亚毫米变形监测精度的要求，需对其进行进一步精化。考虑到全天时高时间分辨率测距(理论上可达到近实时)可提供大量的多余观测，因此，本节将引入加权最小二乘算法，进一步提高谷幅测距精度。

具体地，假定短时间内(比如数小时)谷幅变形值为0，且该时段内有m个距离观测值，据此可建立该时段内谷幅真实距离S与距离观测值L之间的函数模型，为

Am×1S1×1=Lm×1+εm×1

(12)

(13)

式中，P为观测值的权矩阵。

本文采用非参数拟合确定。具体地，首先以全天候测距数据中两岸气象条件相对稳定时刻测距观测值的中值作为参考；然后，将Kalman滤波后的距离观测值与参考值作差，获取各时刻观测值与参考值的差异图(简称“离差”)；之后，采用非参数拟合确定全天时观测值时序离差，并利用时序离差的倒数为全天时最小二乘权重；最后，根据选取的时段提取相应权值，即利用公式(13)求取该时段内的距离估计值。

在获得全天候谷幅测距数据后，即可利用相对于首次观测的距离差作为谷幅变形值。从上述描述中可以发现，本文方法仅依赖于谷幅测距同步的气温、气压和湿度数据，并通过自动挖掘全天候观测数据自身蕴含的信息削弱测距误差，为谷幅变形自动化监测的气象改正提供了全新的模型。

2 研究区域

本文采用锦屏一级水电站的谷幅变形自动化测线验证改正模型的可靠性。锦屏一级水电站拥有目前世界最高的蓄水坝体(305 m)，谷幅变形对于坝体安全的影响巨大。为此，水电站安全监测运维及实施相关单位在水电站坝体下游布设了一条自动化观测线。测距仪采用迪马斯高精度激光测距，同时同步观测两岸的气温、气压和湿度，采样频次为1次/小时。此外，在自动化测线邻近位置布设了人工高精度观测线，为本文模型与方法精度验证提供数据保障。

3 实验与结果分析

根据前述方法，首先采用了传统气象改正模型初步改正全天时自动化测线观测的谷幅距离值，如图1所示。图1展示了该测线2018年12月～2019年11月期间的原始测距值和经过传统模型校正后的距离值。从图1中可以看出，由于谷幅实测气象条件与光电测距参考气象条件的差异，经过传统气象校正模型改正后的距离值与原始观测值存在显著差异。此外，初步改正后的距离值仍存在较大的随机误差，且有一定的趋势误差，需对其进行进一步校正。

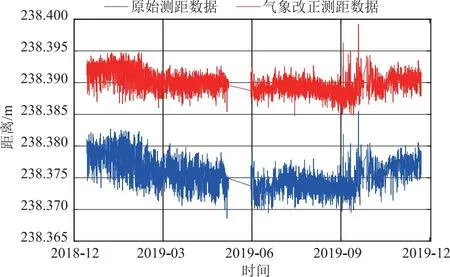
图1 原始测距数据与传统气象改正数据对比

为了更清晰地展示全天候谷幅测距值的趋势性误差，本文首先选取每天气象条件相对平稳时刻的测距值作为参考，并计算24 h距离值与参考值的偏差。图2为锦屏一级水电站在2018年12月～2019年11月期间的小时级测距偏差分布图。从图中可以看出，全天测距偏差存在趋势项误差，且年际尺度的最大振幅超过1 mm，该误差可能会严重削弱全天时形变的监测精度。因此，削弱全天时谷幅测距的趋势项误差至关重要。为此，本文选用了24 h测距离偏差作为样本，采用Fourier级数拟合并去除谷幅测距趋势性误差。图2中曲线为2018年12月～2019年11月期间的日均值离差傅里叶拟合曲线。

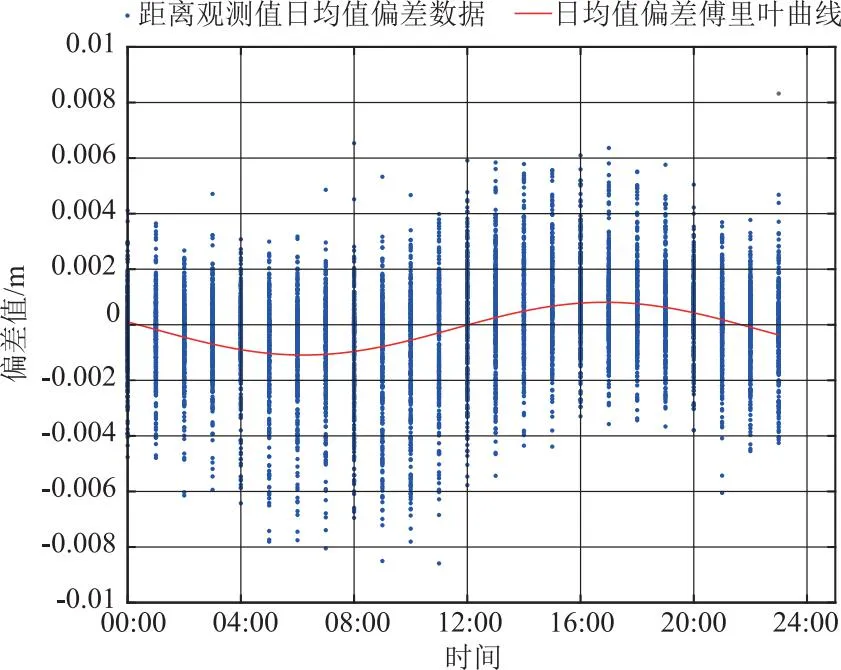
图2 传统气象改正引起的距离日均值偏差

经过趋势项误差削弱和稳健Kalman滤波后的测距数据对比图，如图3所示。图3灰色曲线表示经过趋势项误差校正后的全天时谷幅距离观测值。将图1中的传统气象改正与图3中去趋势项误差后的测距数据作对比，如图4所示。从图4可以看出，相较于传统气象模型校正后的观测值(图1中位于上部的曲线)，谷幅距离变化趋势更清晰，说明本文提出的Fourier级数拟合算法是有效的。然而，从图3中仍可看出，全天时谷幅距离观测值仍包含明显的随机误差，且存在个别差异较大的观测值(称为粗差)。

图3 趋势项误差削弱和稳健Kalman滤波后的测距数据对比

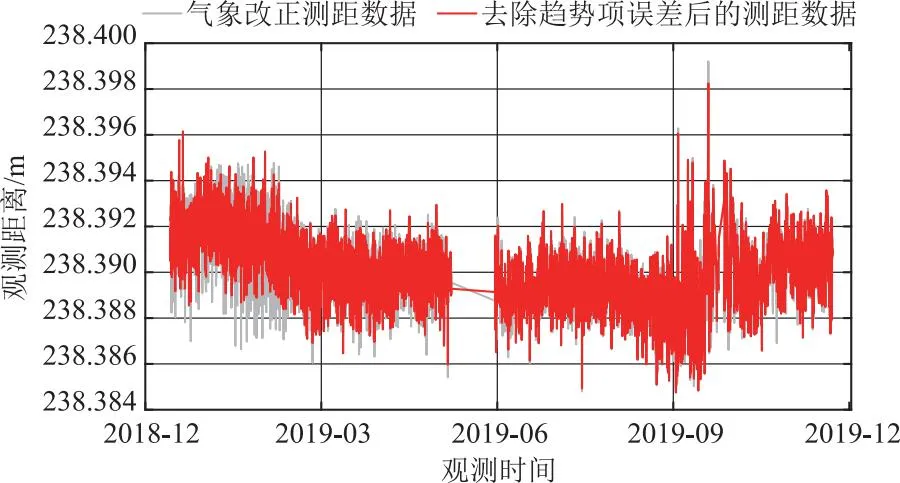
图4 传统气象改正与去除趋势线误差后的测距数据对比

为了更进一步削弱观测随机误差的影响，本文采用了稳健Kalman滤波对去除趋势误差后的测距值进行了改正，其结果如图3红色曲线所示。从图中可以看出，除个别观测点外，大部分观测值的随机误差得到了较好的抑制。与此同时，经过系统性偏差削弱后，谷幅距离变化趋势也逐渐清晰。

最后，本文采用第1.4节中描述的非参数拟合方法确定全天候24 h距离值的权重，并采用加权最小二乘方法估计了该自动化谷幅测线的距离观测值，如图5所示。从图5可以看出，经过加权最小二乘平差后谷幅变形趋势信号较为清晰，即2018年12月开始，该测线的水平距离逐渐增大，表明该地区的谷幅呈现扩张趋势，2019年2月，谷幅迅速收缩，最大收缩幅度达到了6 mm。之后，该谷幅基本保持稳定，到2019年6月有突然的扩张和收缩，随后平稳直至2019年9月，在此之后，该谷幅再一次快速扩张，直至2019年10月迅速收缩，之后便再一次趋于稳定。

图5 谷幅变形自动化测线的加权最小二乘解时序

自动化谷幅变形值与人工测线对比，如图6所示。图6蓝色线为采用加权最小二乘方法估计后该自动化谷幅测线的距离改正值，通过对比和人工谷幅测距结果(图中DY16红色测线)发现，本文方法计算的自动化谷幅测距精度约为0.9 mm，基本能够满足谷幅变形监测对精度的要求。

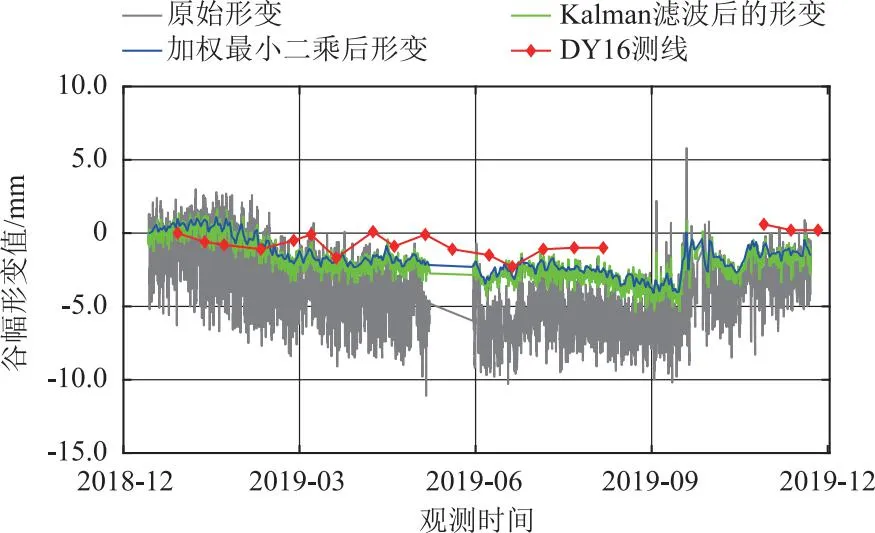
图6 计算的自动化谷幅变形值(蓝色实线)与人工测线(红色菱形)对比

4 结 论

本文提出了一种面向谷幅变形全天时自动化监测的精密气象改正方法，并在锦屏一级水电站中进行了方法测试。实验结果表明：

(1)经过传统气象模型改正后，全天时谷幅距离观测值存在趋势项误差，且本文提出的Fourier级数拟合算法能够有效地削弱该趋势项误差的影响。

(2)经过趋势项误差改正后，全天时谷幅距离观测值仍存在较为显著的随机误差和粗差，而本文提出的稳健Kalman滤波算法和基于非参数拟合的加权最小二乘算法能较好地抑制随机误差和粗差的影响，提高谷幅变形观测精度。

(3)通过与实测数据对比分析，本文提出的算法精度可达0.9 mm，基本符合谷幅变形监测需求。