基于群集控制的多移动机器人运动控制研究

汪明慧 王秋杰

摘要：多机器人运动控制主要包括编队、避障和向目标移动三个方面，文章研究基于群集控制的多机器人的避障和编队协调控制方法，针对复杂障碍物环境下群集控制的局部零势能点问题进行优化设计，并设计基于虚拟领航结构的编队协调控制Leader-follower的编队控制中因leader出现故障无法保持队形的问题。通过Matlab平台和ROS系统的Gazebo平台进行仿真实验验证了算法的有效性。

关键词： 多机器人系统；避障控制；编队控制；群集控制

中图分类号：TP399    文献标识码：A

文章编号：1009-3044（2023）35-0006-04

开放科学（资源服务）标识码（OSID） ：<G：＼飞翔打包文件一＼电脑2023年第三十五期＼2.00xs202335＼Image＼image9.jpeg>

0 引言

多移动机器人已广泛应用于工农业应用管理、空间和海洋探测、环境监测、救灾和国防。随着移动机器人在各领域的发展和应用，对多移动机器人的运动协调提出了更高的要求。在众多的运动协调算法中，一种新的协调方式——群集控制应运而生，群集控制用 “势场”统一实现趋向目标、避障和编队保持，对“势场”进行精确量化又使得群集运动成为一种可度量的运动协调模式，很多研究在不断优化群集控制理论[1-4]。Sakai等人[5]研究提出了一种不区分机器人和障碍物的群集控制算法。Gao等人[6]研究具有切换拓扑的多智能体系统的群集控制问题。Zhang[7]提出一个模型预测的群集控制方法，仅基于相邻测量值设计，建立保证收敛到刚性群的连通性条件。Chen[8]对传统的群集控制算法进行优化，以解决有界空间的跳跃边界引起的问题。Valbuena[9]提出了一种适用于多移动机器人的多功能控制律，控制器可以同时集成群集、编队控制和路径跟踪。Dong [10]从二阶系统的角度分析多智能体在群集运动过程中的稳定性问题。Chen 等人[11-12]则运用动态图理论研究群集控制模型的收敛性问题。Yazdani 等人[13]证明了群集控制在多机器人保持编队和路径跟踪上取得较好的控制效果，Hung [14] 研究有领航者的多智能体群集运动编队控制。

本文采用群集控制方法来实现多机器人的群集运动，将针对复杂障碍物环境下机器人运动存在的两个问题进行优化设计，增强多机器人群集系统的环境自适应能力。其一，当机器人运动环境障碍物密集度程度增加，有复杂凹型障碍物，群集控制会出现“势场陷阱”问题。其二，采用Leader-follower编队方式的多机器人可以通过群集控制进行编队并保持队形向目标前进，但如果领航者机器人出现故障，后面以它为参考点的跟随者机器人也将掉队，编队无法继续保持。本文将提出群集控制的优化模型解决这两个问题。

1 多机器人群集控制模型

群集控制是假设在各个机器人的周围存在一个分布三个区域的势场，这三个区域分别为排斥区域[Rr]、一致区域[Rm]和吸引区域[Ra]，且各个机器人的区域范围一致。当机器人A处于机器人B的排斥区域[Rr]时，机器人A将会受到来自机器人B的斥力，由于各机器人划分的区域一致，所以机器人受到的力将是相互的，即机器人B也会受到来自机器人A的斥力；同理，若机器人处于吸引区域[Ra]则会相互受到引力；而处于一致区域[Rm]则彼此不受到力的影响。每个机器人的势场根据队形的位置确定，当期望队形发生改变，势场也会随之发生改变。该势场能有效地保证各机器人保持一个合适的距离，机器人形成的隊形将会十分稳定。但是有时机器人可能会因为彼此牵扯而导致整体队伍无法前进。本文将通过引入虚拟领航者的方式解决，同时虚拟领航者还可以解决领航者出现状况导致跟随者们跟不上领航者的问题。本文设计的虚拟领航者同样存在势场，但它不会受到其他力的影响，只会受到目标位置的引力影响并对其他机器人产生力。

多机器人队伍有[N]个机器人成员，则用[P=（p1，p2，...，pi，...，pN）]和[V=（v1，v2，...，vi，...，vN）]分别表示[N]个机器人成员的位置向量和速度向量。其中，[vi]应满足如下约束条件：

[vi=vi，  vi≤VmaxVmaxvivi，  vi>Vmax] （1）

式（1）中，[vi]表示第[i]个机器人的速度的模，或者说步长；[Vmax]则表示机器人的最大速度。

当机器人[i]和机器人[j]之间的距离为[δij]时，两个机器人所受到的引力和斥力相等，则[δij]称为机器人[i]和机器人[j]之间的平衡距离。因此，当各机器人间的距离等于平衡距离时，它们彼此的相互作用力为零。

在没有外部环境干扰的情况下，多机器人队伍中，跟随者[i]只会受两种力的影响：一是来自虚拟领航者；二是来自其他跟随者。所受力的大小与跟随者[i]和其他跟随者或者虚拟领航者之间的距离和相对位置有关。根据群集控制的避碰与聚集原则，可建立关于[vi]的速度方程如下：

[vi=gipi-pL+j=1，j≠iNgijpi-pj，  i=1，...，N] （2）

则根据[vi=pi]可定义如下机器人i的运动方程：

[pi=gipi-pL+j=1，j≠iNgijpi-pj，  i=1，...，N] （3）

在式（3）中，[pi∈Rn]，[pj∈Rn]，[pL∈Rn]分别表示机器人[i]，[j]及虚拟领航者的位置；函数[gi∙]为虚拟领航者与机器人[i]的关系函数，函数[gij∙]为机器人[i]机器人[j]的关系函数。

对于[gi∙]和[gij∙]的构造，其表达式如下：

[gipi-pL=-aipi-pLpi-pL1-δipi-pL] （4）

[gijpi-pj=-aipi-pjpi-pj1-δijpi-pj] （5）

在式（4）和式（5）中，[ai∈R+]表示速度参数，速度参数是一个用来调节人工势场函数所产生的力的大小的参数，会对队伍的大小产生影响。它能灵活地调节机器人[i]的势场函数的强度；[pi-pL]表示机器人[i]与虚拟领航者之间的实际距离；[δi∈R+]表示机器人[i]与虚拟领航者之间的平衡距离。当[pi-pL>δi]即[gipi-pL<0]时，虚拟领航者对机器人[i]的势场力表现为引力；相反，当[pi-pL<δi]即[gipi-pL>0]时，虚拟领航者对机器人[i]的势场力表现为斥力。函数[gij∙]与[gi∙]同理。

2 多机器人避障控制

在多机器人的群集运动过程中，由群集内聚性运动分析和聚合群集内成员行为的分析设计出群集控制律，可以使群集机器人实现基本的避碰避障。但对于复杂障碍物，还需要有针对性的避障策略才能解决。本文重点研究机器人在包含凹型障碍物的复杂环境运动时，机器人进入势场的“陷阱”的解决方案。

多机器人在有复杂障碍物的环境下进行运动是采用一种利用势场原理的虚拟物理力方式进行模拟，主要分为两个方面：一方面是集群内部个体间的相互作用；另一方面是附近环境对各个机器人的影响作用，即环境障碍对智能体个体产生的排斥作用和目标位置对个体产生的吸引作用。势场法是一种应用广泛的借助虚拟物理力的路径规划方法，将目标位置看成势能低点，将环境障碍势能高点，机器人在运动过程中，会受到目标位置产生的引力以及环境障碍产生的斥力。令引力和斥力的合力方向作为对象的前进方向，则可以实现机器人既向目标位置移动又远离障碍的避障效果。这些引力和斥力，是一种虚拟物理力。

智能体与目标位置之间的欧几里得距离决定了引力的大小。相对于传统势场，人工势场中目标位置的势能较低，引力势能的大小与智能体和目标位置的距离呈正相关。当距离越大时，智能体所受的引力作用越大，否则越小。[Pr=（xr， yr）]表示机器人的位置信息，[Po=（xo， yo）表示环境障碍的位置信息，Pg=（xg， yg）]表示目标点的位置信息。目标位置对机器人产生的引力场为[Uatt]，障碍物对机器人产生的斥力场为[Urep]。引力势场函数表示为：

[UattP=0.5λ1Pr-Pg2] （6）

[式（6）中，λ1]为引力增益系数；[Pr-Pg]为智能体与目标位置的欧几里得距离。

对势场函数求负梯度，得引力[Fatt]：

[FattPr=-gradUattPr=-λ1Pr-Pg] （7）

环境障碍将会对智能体造成一个与相对位置成反比的斥力，即智能体所受到的排斥作用将随着距离的减小而增大，反之则越小。斥力势场函数定义为：

[UrepPr=0.5λ2（1Pr-Po-1ρ0）2，  Pr-Po<ρ00，  Pr-Po≥ρ0] （8）

式（8）中，[λ2]为斥力增益系数；[Pr-Po]为机器人与环境障碍的欧几里得距离；[ρ0]为环境障碍对机器人产生作用的影响半径。当机器人与环境障碍间的距离超出影响半径[ρ0]时，机器人不会受到来自环境障碍的斥力作用。

同理，对斥力势场函数求解负梯度斥力[Frep]的表达式为：

[FrepPr=-grad[UrepPr]=λ2Pr-Po2（1Pr-Po-1ρ0），  Pr-Po<ρ00，  Pr-Po≥ρ0] （9）

当機器人周围有n个障碍物时，机器人所受到的合力[Ftotal]的表达式为：

[Ftotal=FattPr+i=1nFrepiPr] （10）

合力[Ftotal]的方向即为机器人的运动方向，通常情况下能顺利躲避环境障碍抵达目标位置。

但势场法具有如下一些局限性：

1） 需要实时计算。使用人工势场法作为路径规划方法时，机器人需要根据自身与障碍物和目标点的距离来实时计算所受到的合力。

2） 局部极小值。由式（10）可得，机器人的前进方位与所受合力方向有关。假如机器人受到的斥力合力与引力共线且方向相反时，机器人可能会出现停滞或振荡的情况。

3） 无法抵达目标位置。由式（7）可得，当智能体与目标位置之间的相对位置越近，目标位置造成的吸引作用力越小；而式（9）则表明当智能体与环境障碍之间的相对位置越近，环境障碍造成的排斥作用力将越大。假如在目标位置旁边有障碍且在障碍影响范围内时，机器人所受到的排斥作用可能将大于吸引作用，造成机器人因振荡或停滞而难以抵达目标位置。

这些场景机器人都易发生停滞或振荡现象，对人工势场来说是一个势能极小点，一般对此称机器人落入了“势场陷阱”。解决方法可以通过打破引力和斥力在方向和数值上的平衡。本文采用对斥力进行偏转的方法来使机器人逃离“势场陷阱”。

当机器人所受斥力[Frep]和引力[Fatt]的夹角形成一个较大的钝角或平角时，就存在陷入“势场陷阱”的可能，若将斥力[Frep]的方向偏转一个角度[θ]，使[F]与[Fatt]之的夹角小于直角，则机器人可脱离“势场陷阱”。[θ]是[Frep]的偏转角度，[α]是目标位置到环境障碍与目标位置到机器人的连线夹角，[β]是环境障碍到机器人与目标位置到机器人的连线夹角，[l]是机器人到环境障碍的距离，[Frep]经过偏转得[F'rep]，使合力由[F]变换为[F']。

偏转角[θ]的大小主要与角[β]和距离[l]有关，其表达式为：

[d=l∙sin（β）] （11）

[θ=θ0-μ∙d∙l] （12）

式（12）中，设常数[θ0]为90°，μ是偏转角调整系数，其值为[θ0ρ02]。当[d]不变，距离减小或距离不变，[d]减小时，偏转角度变大。

目标不可达问题的主要原因是目标位置附近的环境障碍给机器人提供的排斥力大于机器人所受的引力。如果目标位置被环境障碍包围，在环境障碍的斥力势场笼罩范围内，即使存在能容纳机器人通过的空间，机器人也难以通过。

假如在保证安全的前提下，斥力增益系数随机器人与环境障碍的距离增加而递减，那么机器人将能够抵达被环境障碍斥力势场包围的目标位置。另外，对于机器人驶过的障碍以及目标位置之后的障碍，可以不必再给机器人提供斥力。因此，本文对斥力增益系数[λ2]进行调整，表达式如下：

[λ2=0，  β≥90° or α≥90°λ0Sr，  β<90° and α<90°] （13）

式（13）中，[λ0]是原系数基数，[S]是机器人与环境障碍之间的距离，[r]是非负实数。

3 多机器人编队协调控制

由于群集控制的编队算法一直保持刚性结构缺乏灵活性，本文设计基于虚拟领航结构的多机器人编队控制算法。由于轮式机器人到达设定的虚拟结构位置所需路程不一定达到最优，使得编队的形成较慢，且需要更多的时间。本文采用任务指定方法对各机器人在虚拟结构中的位置进行分配。步骤如下：

1） 分别计算第[j]个机器人到[j]个虚拟节点的距离，形成距离矩阵Q。

[Q=q11q12…q1nq21q22…q2n⋮⋮…⋮qn1qn2…qnn]       （14）

其中[qij]为机器人[i]到虚拟节点[j]的距离，即

[qij=（xi0-xj）2+（yi0-yj）2]    （15）

2） 在矩阵 Q中找到最小的元素 [Q（ij）]，即虚拟点[j]为第[i]个机器人的预定节点。

3） 删除 Q 矩阵中的第[i]行第[j]列，得到新的矩阵，反复循环，直到 Q矩阵内只剩下一个元素。最终可以得到各机器人与虚拟节点的对应关系。

虚拟领导者和虚拟节点作为领导层，虚拟领导者进行路径规划。运动过程中，跟随机器人在虚拟节点的引力、障碍物的斥力和队形力的合力下，向着各自期望的虚拟领导者，即对应的虚拟节点移动，以提高编队避障中各机器人的灵活性。

虚拟领导者以自身为参考点，生成期望的虚拟结构并在运动过程中形成和维持队形；跟随机器人以期望的虚拟结构中各参考点为目标移动，最终形成相应的队形。移动过程中，障碍物较少情况下多机器人进行编队移动，在较多障碍物情况下，每个机器人作为个体使用人工势场法进行避障，同时在虚拟结构的引导下尽量保持队形。

当动态障碍物向多机器人集群发起碰撞时，处于leader位置的领航机器人会因遭到碰撞而失联，无法继续带领剩余的机器人前行，此时每个机器人会作出相应的障碍物检测，通过比较各个检测结果选出当前的最佳虚拟领航者来带领整个队伍前行。

本文将虚拟结构和leader-follower的结合。虚拟结构的特点是将多个机器人的位姿记录起来，视作一个刚性结构，突出整个机器集群的队形，放大化了整个队伍的队形反馈机制，但是其缺少灵活性，在某些环境下队形的维持需要依靠大量的控制指令，造成较大的资源浪费。通过领航者-跟随者与虚拟结构相结合，将图拓扑与各个节点反馈控制协议交互，完成多机器人的协同控制与容错控制，提高复杂环境下的容错率和灵活性。

编队控制中主要通过位置控制、位移控制、距离控制来实现队形的控制。本文采用位移控制方案，通过领航者跟随者以及分布式控制实现多机器人的编队控制，核心思想为计算出编队队形时各机器人的所在位置，从而计算出领航[leader]和跟随者[followers]的相对位置，控制队形稳定关键在于控制多机器人之间的速度[V]、角度[ω]；其中编队系统的一阶连续模型表示为[Xi=Ui]，其中[Xi]和[Ui]属于[Rn]，[n]表示状态量的维度，[Xi]表示节点i的状态量，[Ui]表示节点i输入量，通过上文图论知识我们可得当且仅当拓扑图G只具有一棵生成树时，系统才可以达到一致性。采用一致性算法表示为

[Ui（K）=ϵjϵNiaij（Xj（k）-Xi（k）-rij（k））]  （16）

其中令[ϵ]> 0，机器人[i]和机器人[j]之间的相对位置表示为[rij]，[k]表示为在某一时刻k。在机器群集刚开始前行时，默认机器人0作为领航者[leader]，通过控制领航者与目标点之间的距离、领航者速度、领航者入度大小实现整个队伍的前进，领航者0的一致性控制算法为

[U（k）=q+tC（k）+iϵNiarij（k）]，[q]和[t]为常数系数。 （17）

4 仿真实验

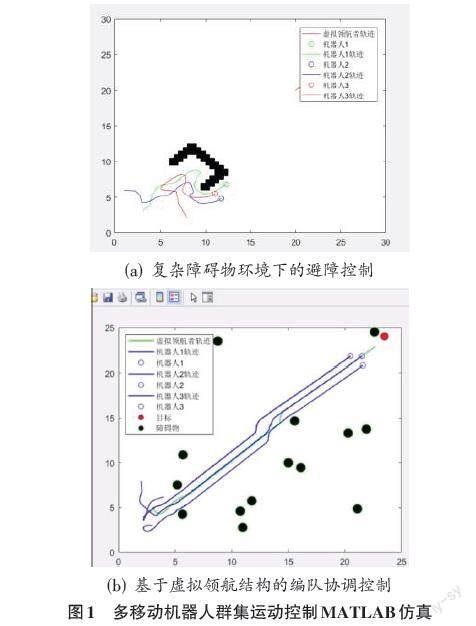
在MATLAB环境下对前面设计的控制算法进行仿真实现。如图1（a） ，黑色不规则物体为凹型障碍物，此环境是容易造成势场陷阱导致机器人无法逃离，在优化后的群集控制算法下，机器人能逃离势场陷阱。仿真图中不同颜色的圆圈代表不同机器人个体，不同颜色的曲线代表各机器人的运动轨迹。可以看出，本文设计的优化模型能解决传统群集控制存在的势场陷阱问题。如图1（b） ，是检验本文设计的基于虚拟结构体的一致性编队协调算法，虚拟领导者进行路径规划，跟随机器人在虚拟节点的引力、障碍物的斥力和队形力的合力下，向着虚拟领导者，即对应的虚拟节点移动，此设计提高编队避障中各机器人的灵活性。

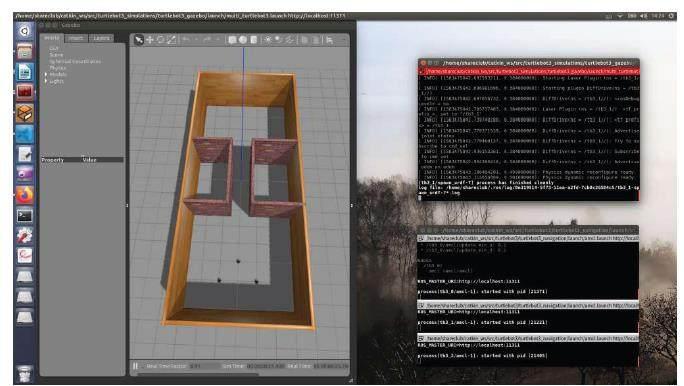
本文还在ROS环境对基于群集控制的多机器人运动控制算法进行仿真实验验证算法的有效性，仿真结果如图2。图2左边为gazebo的仿真可视区，右边为启动命令终端。仿真显示优化后的群集控制算法能使所有的机器人移动在一起，避免碰撞并向目标移动。

5 结束语

本文研究基于群集控制的多机器人的避障控制和编队协调控制。针对群集控制会出现的“势场陷阱”问题，设计了斥力偏转策略解决人工势场下局部零势能点问题。并针对Leader-follower的编队控制会因leader出现故障编队无法继续保持的问題，采用基于虚拟领航结构的编队协调控制算法，通过领航者-跟随者与虚拟结构相结合，将图拓扑与各个节点反馈控制协议交互，提高复杂环境下的容错率和灵活性。通过仿真实验验证了算法的有效性。

参考文献：

[1] Valbuena Reyes L A，Tanner H G.Flocking，formation control，and path following for a group of mobile robots[J].IEEE Transactions on Control Systems Technology，2015，23（4）：1268-1282.

[2] Saulnier K，Saldana D，Prorok A，et al.Resilient flocking for mobile robot teams[J].IEEE Robotics and Automation Letters，2017，2（2）：1039-1046.

[3] 毛昱天，陈杰，方浩，等.连通性保持下的多机器人系统分布式群集控制[J].控制理论与应用，2014，31（10）：1393-1403.

[4] 董慧.基于偏微分方程约束的机器人群集运动控制系统设计[J].计算机测量与控制，2023，31（4）：130-135.

[5] Sakai D，Fukushima H，Matsuno F.Flocking for multirobots without distinguishing robots and obstacles[J].IEEE Transactions on Control Systems Technology，2017，25（3）：1019-1027.

[6] Gao J Y，Xu X，Ding N，et al.Flocking motion of multi-agent system by dynamic pinning control[J].IET Control Theory & Applications，2017，11（5）：714-722.

[7] Zhang H T，Liu B，Cheng Z M，et al.Model predictive flocking control of the cucker-smale multi-agent model with input constraints[J].IEEE Transactions on Circuits and Systems I：Regular Papers，2016，63（8）：1265-1275.

[8] Z. Chen， H. T. Zhang， M. C. Fan， D. Wang and D. Li.Algorithms and experiments on flocking of multiagents in a bounded space[J].IEEE Transactions on Control Systems Technology，2014，22（4）：1544-1549.

[9] Valbuena Reyes L A，Tanner H G.Flocking，formation control，and path following for a group of mobile robots[J].IEEE Transactions on Control Systems Technology，2015，23（4）：1268-1282.

[10] Dong W J.Flocking of multiple mobile robots based on backstepping[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B （Cybernetics），2011，41（2）：414-424.

[11] Chen H Y，Wang C，Lou Y J.Flocking multiple microparticles with automatically controlled optical tweezers：solutions and experiments[J].IEEE Transactions on Biomedical Engineering，2013，60（6）：1518-1527.

[12] Wang Z Y，Gu D B.Cooperative target tracking control of multiple robots[J].IEEE Transactions on Industrial Electronics，2012，59（8）：3232-3240.

[13] Yazdani S，Haeri M.Flocking of multi-agent systems with multiple second-order uncoupled linear dynamics and virtual leader[J].IET Control Theory & Applications，2016，10（8）：853-860.

[14] Hung S M，Givigi S N.A Q-learning approach to flocking with UAVs in a stochastic environment[J].IEEE Transactions on Cybernetics，2017，47（1）：186-197.

【通聯编辑：朱宝贵】