多策略融合的粒子群优化算法*

王惠敏,孙 滢,高岳林

(1.北方民族大学 计算机科学与工程学院,宁夏 银川 750021;2.北方民族大学 数学与信息科学学院,宁夏 银川 750021;3.宁夏智能信息与大数据处理重点实验室,宁夏 银川 750021)

群智能优化算法是一种受生物群体行为启发而提出的优化技术,是计算智能4个分支中的重要一支。由于群智能优化算法具有快速性、并行性和鲁棒性的优点,近年来迅速发展并成为优化领域的热点研究方向之一。传统智能优化算法存在如算法规模冗余、复杂度过高、运算时间较长等缺点,而群智能优化算法可以通过模拟生物行为来弥补这些缺点,并在该领域取得了丰富的成果[1-3]。群智能优化算法包括模拟鸟群觅食行为的粒子群优化算法(Particle Swarm Optimization, PSO)[4-5],模拟萤火虫发光吸引其他个体的萤火虫算法(Firefly Algorithm, FA)[6],模拟海鸥群体迁徙和捕食的海鸥优化算法(Seagull Optimization Algorithm, SOA)[7]和模拟麻雀群体觅食行为的麻雀搜索算法(Sparrow Search Algorithm, SSA)[8]等类型。

传统PSO[4]算法最初设计用于解决连续搜索空间中的函数极值问题,具有结构操作较为简单、参数设置较少、计算内存较小、收敛速度较快、算法性能优越以及易于实现的优点。该算法提出后得到了研究者的广泛关注,用于解决实际优化问题,例如路径规划问题[9]、参数辨识问题[10]和图像处理问题[11]。然而,随着信息技术的发展,实际优化问题越来越复杂,传统PSO算法面临着收敛精度不高、易陷入局部最优的严峻挑战。针对这些问题,研究者们提出了许多改进的PSO变体,以提高算法的性能。LUO et al[12]提出的带有压缩因子的PSO算法改善了粒子难以跳出局部最优的问题,并提高了算法的收敛速度,在工程优化问题的解决中取得了显著效果。一些研究者将离散问题的搜索空间映射到连续粒子运动空间中,成功地将PSO算法应用于解决离散问题[13],并通过改变粒子的邻域拓扑结构提升算法的性能。许胜才等[14]将PSO算法与不同的拓扑结构相结合,使得粒子在前期能够保证搜索范围的同时在后期提高整个种群的收敛性,从而提高了算法的整体性能。相较于传统PSO算法,量子PSO算法能够保证粒子种群的多样性并且防止算法过早收敛。李玥等[15]提出了改进的量子PSO算法,采用高斯扰动的局部吸引子和粒子加权方法,显著提高了算法的优化精度和稳定性。此外,研究者们在调整参数取值、结合优化策略或混合其他算法等方面做了许多改进工作。参数的选择对算法也有不同程度的影响,目前比较流行的对惯性权重的选取策略仍然是SHI et al[16]提出的线性动态递减惯性权重策略,在进化过程中增加了勘探和开发能力。改进粒子的速度和位置更新公式以提高算法性能是目前的研究热点之一。李二超等[17]将粒子速度更新公式中个体最优和群体最优替换为其线性组合,提高了粒子之间信息共享的程度,增加了解的多样性。引入其他智能优化算法特性能够得到性能更优的混合算法,闫群民等[18]引入模拟退火操作提出的自适应模拟退火PSO算法,避免了PSO算法陷入局部最优解。KASEB et al[19]则在PSO算法中加入遗传算法的交叉算子和变异算子,进一步平衡算法的勘探与开发能力,改善了处理城市的风力条件的能力。

当前虽有大量的改进研究,但PSO算法的性能仍有进一步提升优化的空间。为了改进标准PSO算法搜索精度较差和易陷入局部最优的缺点,本文提出一种多策略融合的粒子群优化(Multi-strategy Fusion Particle Swarm Optimization, MFPSO)算法。本文的贡献如下:

(1)提出均值自适应判断机制,有效判别粒子处于开发阶段。自适应均值判断机制与逆向思维的权重相呼应。提出的逆向思维的权重有利于提升算法的稳定性以及全局寻优的效率,并且能够保证粒子的质量和提升收敛速度。在局部寻优时,扩大粒子的搜索范围,避免后续粒子陷入局部最优,从而获得更优结果。

(2)引入线性组合速度更新公式、自适应位置更新公式,增加了全局搜索中粒子找到更优位置的可能性,增加了解的多样性,使算法朝着最优解的方向演化。

(3)提出基于爬山算法思想[20]的局部搜索策略,通过随机步长调整粒子的位置,降低粒子陷入局部最优的概率。

(4)通过消融实验对MFPSO算法的各个组件进行了验证,并将其与标准PSO算法[5]、IPSO-VP算法[17]、SA-PSO算法[18]以及其他3种群智能优化算法(FA[6],SOA[7],SSA[8])进行对比实验。在12组测试函数中对每个算法进行对比实验,以验证本文所提MFPSO算法的有效性。实验结果表明,MFPSO算法的收敛速度和收敛精度均优于对比算法,提升了传统PSO算法的性能。

1 标准PSO算法

(1)

(2)

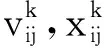
粒子i在第k+1次迭代中的速度、位置边界条件公式为:

(3)

(4)

个体、全局位置更新公式为:

(5)

(6)

公式(5)(6)中,函数f所得到的结果是适应度函数值。根据f来更新粒子群中个体极值pbesti和全局极值gbest的值,让粒子i向着更好的方向进行迭代寻优。

2 MFPSO算法设计

2.1 基于均值自适应判断机制的逆向思维惯性权重策略

群智能优化算法的寻优过程一般分为全局勘探和局部开发2个阶段。由于群智能算法有很大的随机性,使用恰当的适应度值特性判别条件作为评判搜索阶段的参考指标更有意义。更好的判断机制能够帮助算法提升解的质量,很多学者对此有不同的见解[17,21]。均值通常被用来体现一组数据的集中趋势。在迭代过程中,当前适应度值小于均值时,说明算法距最优值还有一定的偏差,粒子分布较为分散,此时适用全局搜索策略,提高算法的寻优速度和粒子质量。当前适应度值大于均值时,说明该粒子与粒子群整体的距离较小,粒子分布较为集中,此时适用局部搜索策略,扩大粒子的寻优范围避免陷入局部最优。均值自适应判断公式为:

(7)

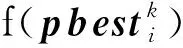
w是标准PSO算法最重要的参数之一。惯性权重线性递减策略提出较早,并未充分考虑到迭代过程中惯性权重与粒子整体适应度值变化的关联[22]。有学者经理论分析证实了权重线性递增策略的有效性。本文结合均值自适应判断机制创新性地提出逆向思维的惯性权重,前期粒子移动较后期有更大的随机性,引入较小的w保持搜索精度,后期不需要一味地提高搜索速度,引入较大的w扩大粒子的搜索区域,避免粒子陷入局部最优。同时采用小范围线性递增的w,能够提升整个算法的稳定性。逆向思维的惯性权重公式为:

该公式为惯性权重的调整提供了全新视角。根据参考文献[17],此处人为设定wmin=0.4,wmax=0.9。(wmax-wmin)×0.2为惯性权重的值,根据进化进程在20%范围内递增或递减。在全局搜索时采用较小的w减少粒子在没有希望的区域飞行,从而提高了解的质量;在局部搜索时采用较大的w保证解的多样性,避免算法早熟收敛。

2.2 线性组合速度更新和自适应位置更新公式

当算法处于全局搜索阶段时,个体最优和群体最优的线性组合速度更新策略[17,23]能够有效提升PSO算法的勘探能力和解的可靠性。粒子将从此线性组合中调整粒子间的影响力,更新速度。线性组合速度更新公式为:

(9)

自适应位置更新策略[21]具有不同的探测和开发能力。在勘探和开发阶段采用不同的位置更新公式能够提升算法的整体性能。位置更新公式(2)能够保证算法局部勘探能力,帮助算法跳出局部最优,而将惯性权重引入位置更新公式中能够提升解的精度,有助于加快算法的收敛速度,提高算法的全局开发能力。自适应位置更新公式为:

(10)

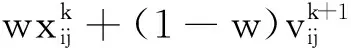
2.3 爬山算法思想

爬山算法[20]是对深度优先搜索的一种改进,在结合其他算法解决实际问题时非常有效[24]。爬山算法从当前解的最近解空间中选择最好的解作为当前解,只有在算法改进的情况下才会接受新的解。由于爬山算法是一种局部择优的方法,所得的解无好坏之分,粒子不会只向着大部分粒子认为有希望的地方飞行,这一缺陷恰好成为了MFPSO算法的优点,使算法有更多的机会得到其他的解,有效避免粒子陷入局部最优。基于爬山算法思想的公式组为:

(11)

(12)

公式(11)中,当前全局最优值的邻居极值rbestk的位置由当前全局最优值gbestk的位置加入随机步长rand得到邻居极值,其中rand∈[0,1]。公式(12)中,将邻居极值rbestk的值与当前全局极值gbestk的值进行比较,若f(rbestk)≤f(gbestk),则gbestk=rbestk;反之则保持不变。

2.4 MFPSO算法的整体流程

MFPSO算法的优异性体现在:(1)提出均值自适应判断机制,使得粒子选择更合适的更新方式进行寻优,从而逐步提升解的质量;引入逆向思维的惯性权重,在全局搜索时保持较小的搜索范围保证一定的精确度,提供较优解,在局部搜索时保持较大的搜索范围,避免陷入局部最优;(2)引入线性组合速度更新公式,这一组合结合了社会认知部分和个体认知部分,寻优时2个部分充分发挥作用,调整了全局最优粒子的影响力。引入自适应位置更新公式,加快解的收敛速度;(3)引入爬山算法思想,使粒子跃出局部最优。通过以上改进,让算法朝着更好的方向进化,最终提升标准PSO算法的整体性能。算法伪代码如下。

算法1MFPSO算法伪代码

Input:初始化MFPSO算法参数,包括种群N,维度D,迭代次数K,学习因子c1和c2,惯性权重w,位置边界xmax和xmin,速度边界vmax和vmin。

Ouput:最优适应度值

1: 随机生成初始化种群并且初始化粒子的位置和速度

2: 利用式(1)和式(2)计算种群的适应度值

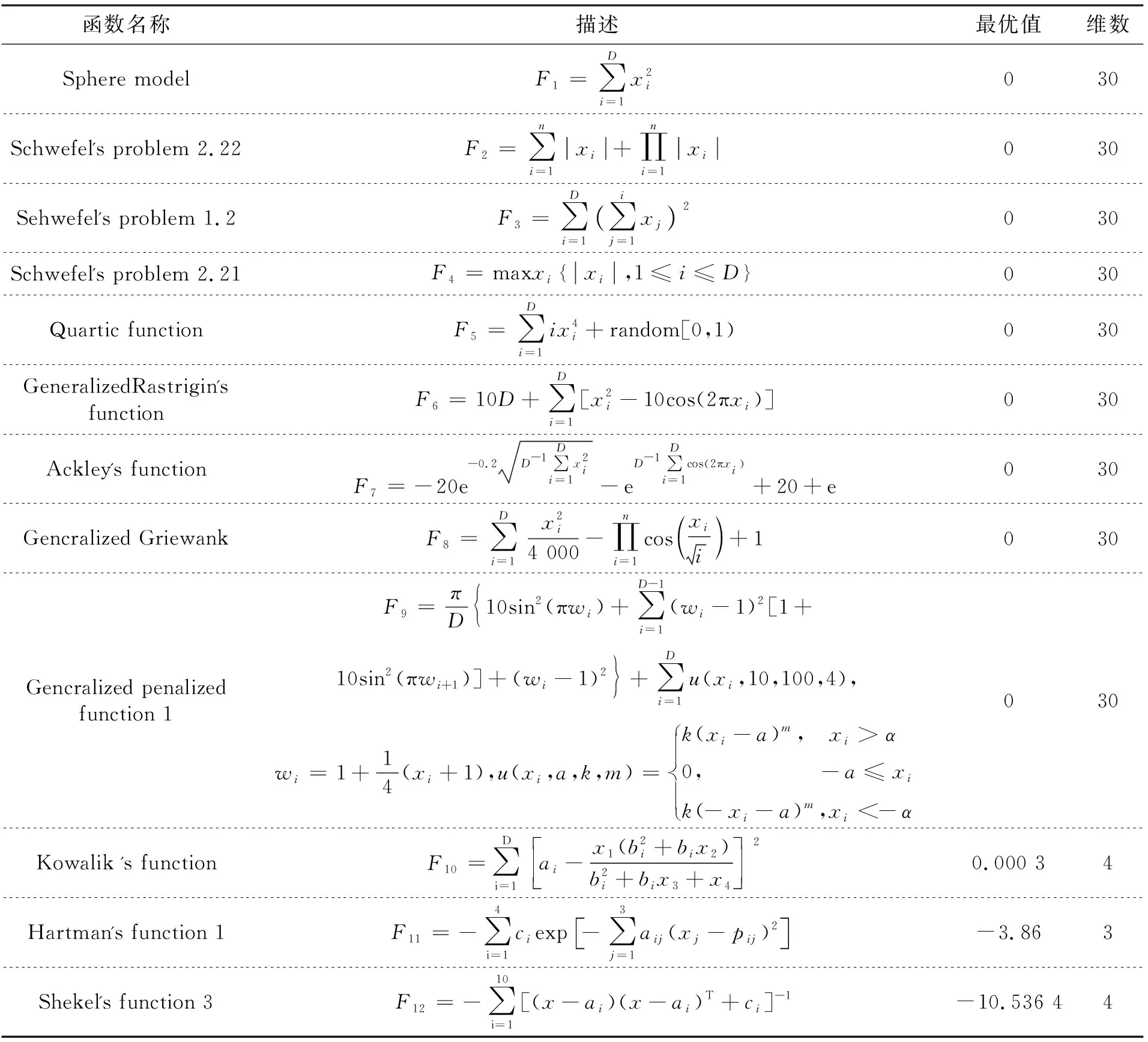
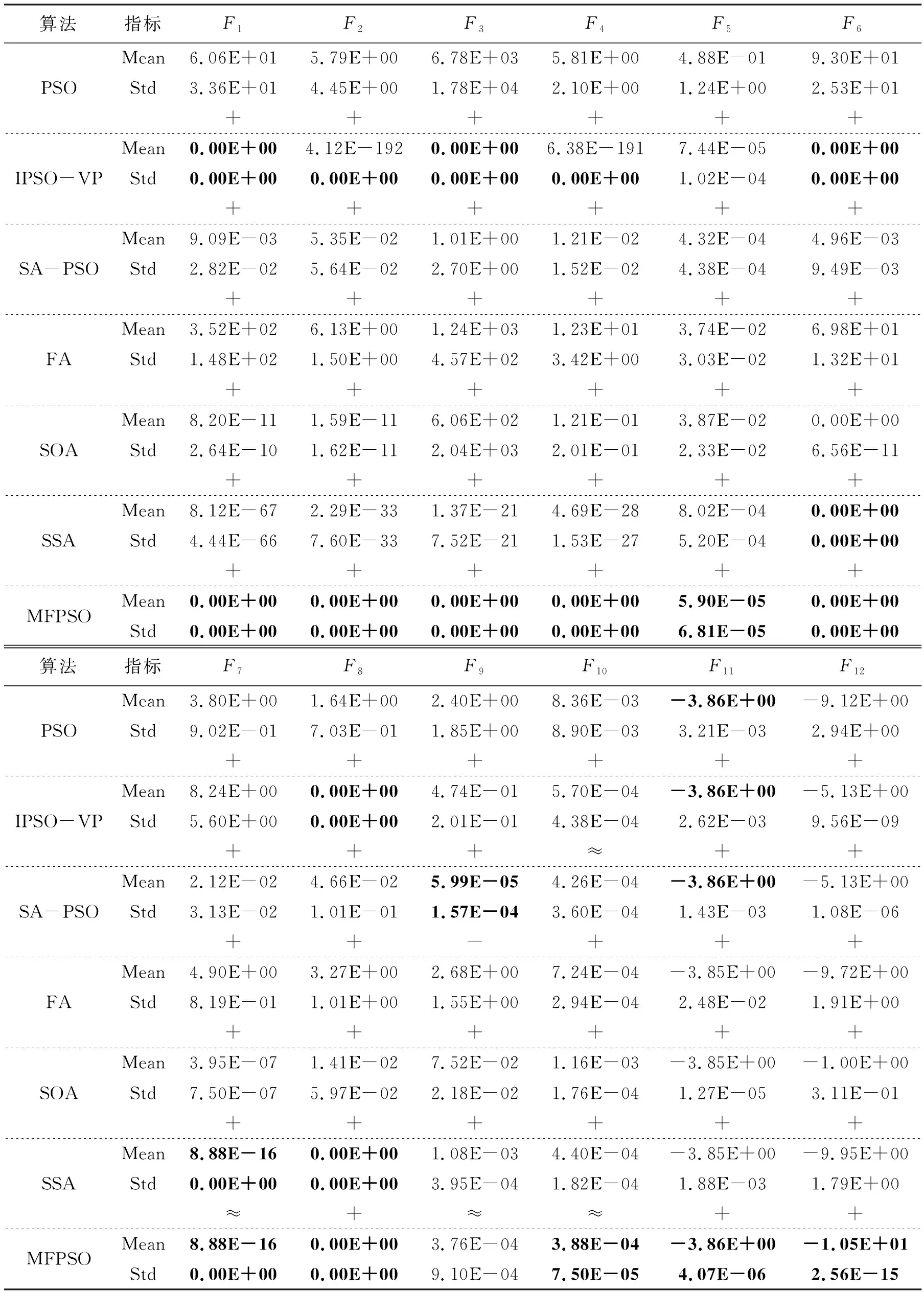
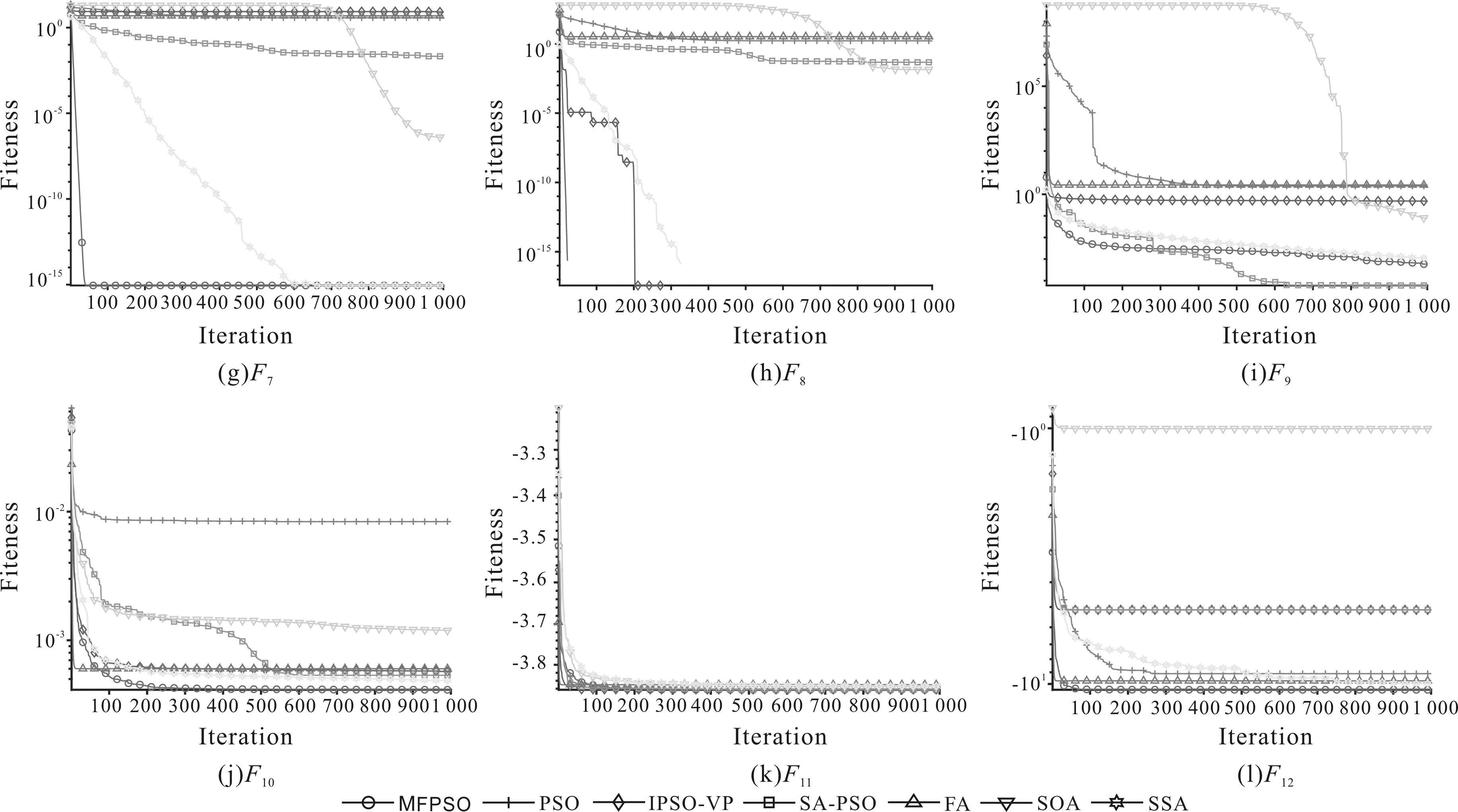
4: whilek

5: 利用式(7)判断本次更新方式

6: 利用式(8)更新惯性权重w

7: fori=1 toN

10: 更新个体计算适应度值

13: end if

15: 利用式(6)更新gbestk+1

16: end if

17: 利用式(11)和(12)更新gbestk

18: end for

19:k=k+1

20: end while

3 仿真实验

本文实验环境配置为Intel(R) Xeon(R) E-2224 CPU@3.40GHz,内存16 GB,使用MATLAB2021b实验平台进行仿真。为了验证算法的有效性,选取不同类型的测试函数进行消融实验与对比实验。MFPSO算法、IPSO-VP算法[17]、SA-PSO算法[18]、FA[6]、SOA[7]、SSA[8]分别在每组测试函数独立运行30次,每个算法的迭代次数为1 000次。在本次实验中,平均值代表算法运行30次找到全局最优解的均值,标准差代表算法30次实验找到解的稳定程度。性能指标均越小越好,表现最好的用粗体表示。

3.1 测试函数选取

本文在经典测试问题[25]中选取12个测试函数用于仿真实验。由于算法在不同类型的测试函数上表现不同,选取F1-F4为单峰函数,用于证明算法的收敛速度和寻优精度;F5-F9为多峰函数,是局部最小值的数量随维数呈指数增长的多模态函数;F10-F12为固定维函数,只有部分局部极小值。函数具体名称及全局最优值见表1。

表1 测试函数Tab. 1 Benchmark functions

3.2 消融实验与分析

为了验证MFPSO算法各个部分的有效性,选择基于均值自适应判断机制的逆向思维的惯性权重优化策略(S-PSO)。在除去自适应判断机制的情况下选择逆向思维的惯性权重分别应用全局优化策略(G-PSO)和局部优化策略(P-PSO)进行消融实验。为节省空间,选取单峰函数F1、多峰函数F9、固定维函数F10进行消融实验,实验结果见表2。

表2 消融实验结果Tab. 2 Ablation experiment results

从表2可以看出,仅靠一个全局优化策略或者局部优化策略的力量是不够的,单个优化策略对标准PSO算法有或多或少的改进,但是求解精度远不及MFPSO算法。G-PSO策略在单峰函数F1上取得了很好的成绩;在F10中的实验结果比P-PSO策略相对较好,但收敛速度比MFPSO算法慢,说明G-PSO策略需要执行局部优化策略来进一步提升寻优能力。P-PSO策略和S-PSO策略在3组实验中的效果均没有MFPSO算法好,P-PSO策略开始时在质量较低的解中寻优会造成算法早熟收敛,而在较优解附近进行寻优更有可能提升算法整体性能。S-PSO策略说明惯性权重的选取对算法整体性能影响很大,并且在F10中最优值表现很好。只有有效的优化策略相互补充才能更好地提升算法的整体性能,这进一步说明本文所提MFPSO算法的有效性。

3.3 实验结果数值实验与分析

为了进一步验证本文所提算法的有效性,将MFPSO算法与标准PSO算法、IPSO-VP、SA-PSO、FA、SOA、SSA在上述选取的测试函数中进行对比实验,并进行实验结果分析。本文对标准PSO算法进行改进,以标准PSO算法作为判别MFPSO算法性能的基准。同类型对比算法选取了包含不同优化策略和混合其他智能优化算法的改进PSO算法变体进行比较,体现MFPSO算法的优异性能。对比算法的参数选取遵循相应文献中的默认设置。实验结果如表3所示,收敛曲线如图1所示。

表3 MFPSO算法与对比算法的实验结果Tab. 3 Experimental results of MFPSO and comparative algorithms

图1 收敛曲线Fig. 1 Convergence curve

由表3可知,在F1和F3中,MFPSO算法、IPSO-VP算法、SSA均可以找到其全局最优值,其余4种对比算法均未找到理论最优值。其中SSA并不能每一次都找到全局最优,稳定性较低,MFPSO算法在这2组实验中以稳定性获胜,这可能是由于MFPSO算法中的自适应速度、位置更新公式增大了粒子间的信息共享能力,从而有效提高了粒子质量并且提升了算法的收敛速度。在F2中,IPSO-VP算法相较于其他对比算法有更高的精度并且稳定性更强。然而,通过图1中收敛曲线可知,MFPSO算法找到全局最优的速度更快,更具竞争性。在F4中,尽管IPSO-VP算法和MFPSO算法具有较高的稳定性,但只有MFPSO算法可以找到全局最优值,收敛精度更高。IPSO-VP算法、MFPSO算法和SSA在F6和F8中都取得了平均最优值,而MFPSO算法的收敛速度更快。这可能是由于爬山算法避免了粒子陷入局部最优,使算法不断朝着全局最优的方向进化。在F7中,MFPSO算法和SSA优于其他对比算法,并且在获得相同求解收敛精度的同时标准差最小。在F9中,SA-PSO算法在平均最优值、标准差指标上取得了本组实验中最好的成绩,MFPSO算法则排名第二。在F5,F10-F12中,MFPSO算法取得更好的平均最优值且发挥稳定,说明在自适应判断机制的逆向思维的惯性权重变化较小时,有利于提升PSO算法的稳定性。

仅从以上指标出发衡量各优化算法的整体性能还不足以说明MFPSO算法的优异性能,需要进一步进行Wilcoxon秩和检验以证明MFPSO算法比其他6种对比算法具有显著的性能优势。表3中,“+/≈/-”表示MFPSO算法优于、近似于、劣于相应的对比算法。从统计结果可以看出,MFPSO算法的性能分别在F1-F6,F8,F11和F12这9组测试函数上显著优于上述6种对比算法;在F7和F10这2组测试函数中与相应对比算法获得相似的结果;仅在F9中劣于AS-PSO算法。因此,MFPSO算法在上述12组基准函数上具有较好的性能,说明通过基于均值自适应判断机制的逆向思维惯性权重策略、线性组合速度更新策略、自适应位置更新策略以及爬山算法对标准PSO算法的改进能够有效平衡算法的勘探与开发能力,提升算法的搜索性能。

从收敛速度出发,图1中能够明显发现在面对相对容易寻优的单峰函数F1-F4时,MFPSO算法在寻优过程中的速度优势突出,且具有较高的精度。在F5中,IPSO-VP算法在前期表现最好,但是MFPSO算法后期收敛精度较高。后期大部分算法的粒子受全局历史最优个体粒子的影响较大,越来越多粒子被诱到局部最优解处,此时大多数粒子跳出局部最优位置的能力不断降低,大部分对比算法已经陷入局部最优。MFPSO算法在迭代后期利用爬山算法为粒子提供了跳出局部最优的能力,可以不间断地更新全局最优,从而提高寻优精度。在复杂多峰函数F6-F8中,寻优难度增加,但MFPSO算法仍然表现出了较好的收敛速度和精度,拥有最好的寻优性能。SA-PSO算法的优势突出体现在其融合模拟退火操作,但只在F9这组函数中表现较好,此时MFPSO算法的寻优结果仅次于SA-PSO算法。在函数F10-F12中,随着迭代的不断进行,各个算法的收敛速度都较为缓慢,但MFPSO算法以精度优势取得了较对比算法更好的成绩。

通过以上仿真实验和结果分析可知,相较于6种对比算法,MFPSO算法在收敛精度和收敛速度上都体现出了较大优势,整体性能更好。这说明本文所提3种改进策略切实有效,使得算法具有良好的全局搜索能力和跳出局部最优的能力,是一种值得采纳和推广的改进算法。

4 结束语

标准PSO算法在寻优时存在收敛速度较慢、收敛精度较低和易陷入局部最优等缺陷。针对以上不足,本文提出了MFPSO算法。首先,该算法通过引入基于均值自适应判断机制的逆向思维惯性权重,在不同阶段使用不同的更新方式帮助算法找到更好的寻优结果。其次,引入了线性组合速度和自适应位置更新公式,调整了粒子之间的信息共享程度,增加了全局搜索时解的精度,从而提升了收敛速度。最后,利用爬山算法思想在局部搜索时给粒子提供更多找到全局最优解的机会。相较于其他先进算法,各项仿真实验结果表明MFPSO算法取得了最好的效果,提升了PSO算法的整体性能。然而,在个别数值实验中MFPSO算法的表现还不够理想,今后将继续改进算法,提升算法在不同问题中的表现。