同步卫星漂移问题研究

黄俊杰

(江苏省海门中学, 江苏 南通 226100)

地球同步卫星轨道的空间资源是十分有限的,一方面不能在赤道上空无限制地发射同步卫星,另一方面,所发射的同步卫星也无法保证一定是在作圆轨道运动,它有可能会在同步圆轨道附近做离心率很小的周期为24 h椭圆运动．如图1所示,24 h椭圆轨道上P、P′点,椭圆轨道卫星的角速度等于同步圆轨道卫星的角速度,即ω=ω0.假定初始时刻,椭圆轨道卫星位于P′点,同步圆轨道卫星位于Q′点,在近地心区域P′AP范围内,椭圆轨道的角速度比同步圆轨道的角速度大,即椭圆轨道卫星追及直至超越同步轨道卫星到达椭圆轨道P点,同步圆轨道卫星落后到达Q点.在远地心区域PA′P′内,椭圆轨道的角速度比同步圆轨道小,同步圆轨道卫星反过来追及椭圆轨道卫星直至超越椭圆轨道卫星到达轨道Q′点,椭圆轨道卫星落后到达P′．椭圆轨道卫星与同步圆轨道卫星间的追及与反追及的周期性运动,在以同步圆轨道卫星的转动参考系中,椭圆轨道卫星在同步圆轨道卫星附近做周期性的往复运动,这里形象地称为椭圆轨道卫星相对于同步轨道卫星的“漂移”运动．

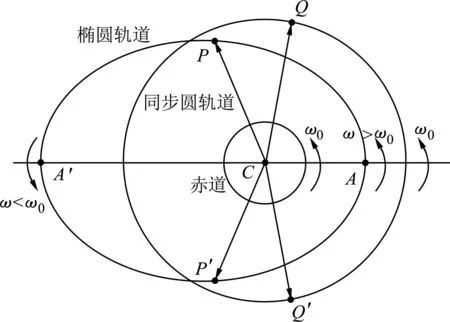
图1 地球同步卫星轨道

技术上对这类“漂移”是有一定的限制的,通常修正这类“漂移”是通过卫星自带的动力系统完成的．在中学物理培优教学中,对这种离心率很小的椭圆轨道卫星相对于同步圆轨道卫星的“漂移”运动的研究,对提升学生应用数学知识解决物理问题的能力具有较大的价值．下面选用一道卫星“漂移”问题进行分析探究以加深对这类问题的理解．

例1.假定各国在发射卫星时都遵从以下规定：卫星进入轨道后不可离开本国领土和领海对应的领空,即卫星与地心连线和地球表面的交点必须落在自己的领土或领海上．为下面讨论需要,给出同步卫星的轨道半径R0=4.2×104km．

下面分析一个具体问题：某国发射一颗周期为T0=1天的不用动力飞行的卫星,卫星的轨道平面位于赤道平面内．容易理解,如果卫星取一椭圆轨道,那么它相对于地心的角速度就不是定值,与地面上的参考点之间会发生相对运动．假设这个国家仅有θ=2°经度范围的赤道领空,发射者就必须将卫星轨道的偏心率e限制在一个很小的范围内,以保证卫星不离开本国领空．试确定偏心率e的最大可取值．

解析1：平面直角坐标系分析.

依题意,若这个国家仅拥有θ=2°纬度范围的赤道领空,而椭圆轨道卫星又不能离开这个领空,则依据对称性,椭圆轨道卫星相对于赤道只能在这个2°的纬度范围内作往复运动．由于赤道绕地心转动的角速度,即地球自转角速度ω0为一定值,则卫星相对于地心转动的角速度ω只能在ω0±Δω的小幅范围内变动．

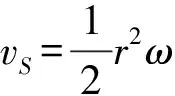
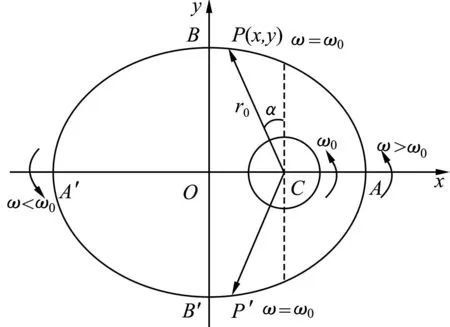
图2 卫星的椭圆轨道与赤道位置关系示意图

P、P′右侧ω>ω0,卫星相对赤道朝东飞行,设累积的偏转角度为θ东;P、P′左侧ω<ω0,卫星相对赤道朝西飞行,设累积的偏转角度为θ西．由椭圆轨道卫星相对于赤道在一定经度范围内的往返运动的周期性可得θ东=θ西,由于题中要求卫星不离开该国仅有的θ0=2°经度范围的赤道领空,则有θ东=θ西≤θ0=2°．

我们知道,对于圆轨道的同步卫星(偏心率e=0),是不会产生累积的偏转角度的,所以,上述累积的偏转角θ东、θ西都是由于椭圆轨道的角速度变化造成的．

下面选取θ东来讨论卫星在该国上空单向漂移的情况．

设卫星在P′点时恰好在该国赤道领空区域的西侧边界,卫星转到P点时恰好处在该国赤道领空区域的东侧边界,卫星由P′运动到P的过程相对于赤道累积转动的角度为θ东．而后卫星又将相对赤道移到赤道领空东侧边界,如此往复．

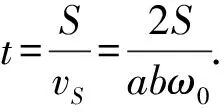
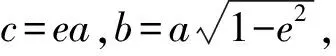
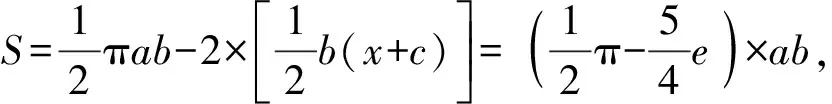
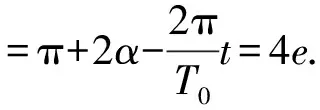
解析2：平面几何分析.

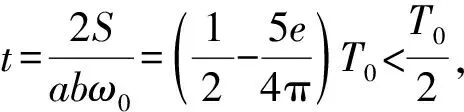
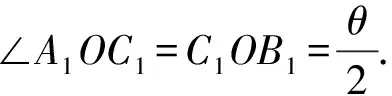
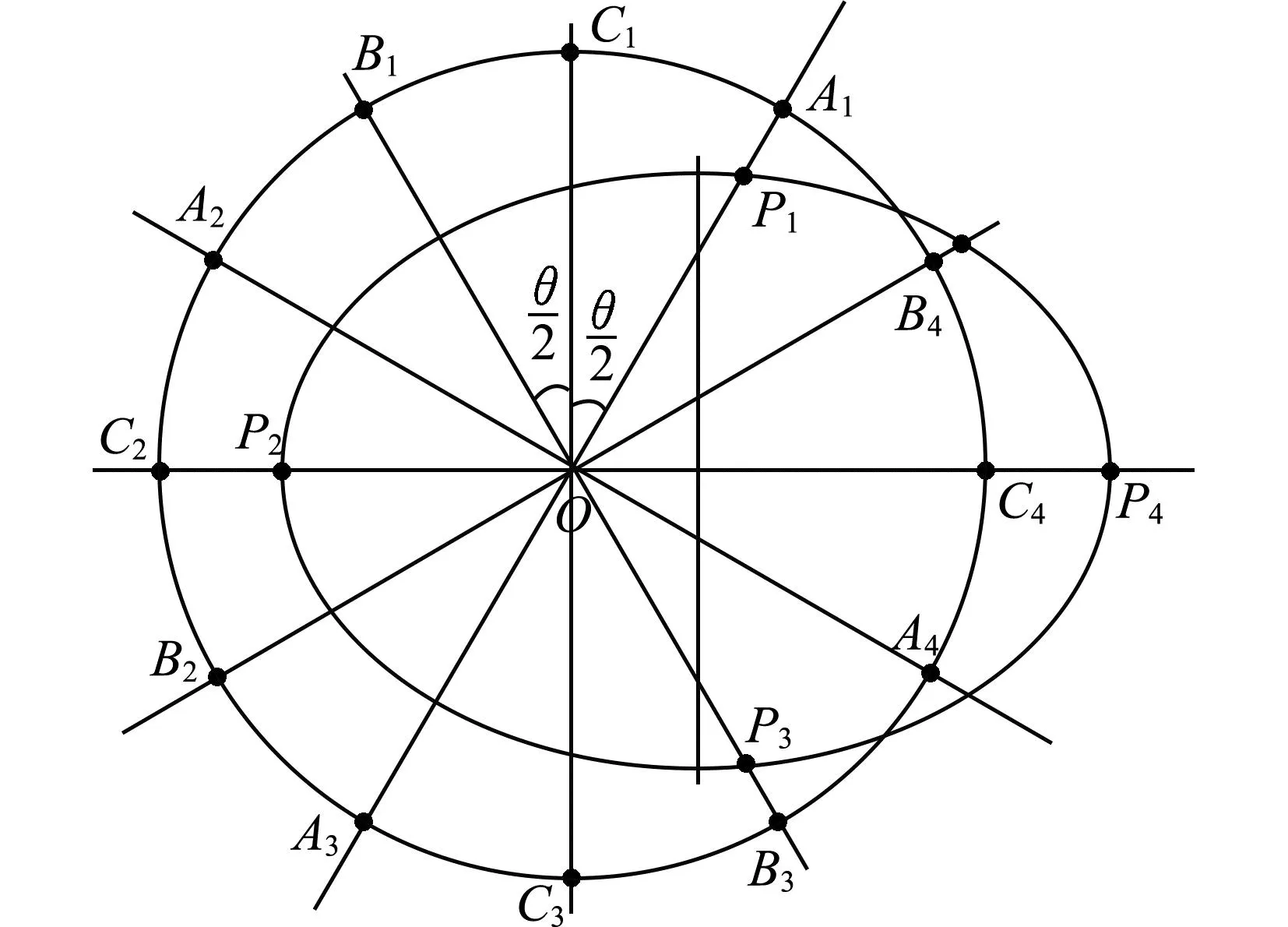
图3 将赤道转动用同步圆轨道卫星运动代替

可以认为要使椭圆轨道卫星相对于同步圆轨道卫星始终位于θ经度范围内,需满足前T/2椭圆轨道卫星P追同步圆轨道卫星,后T/2同步圆轨道卫星追椭圆轨道卫星P．我们用椭圆轨道的矢径OP与同步圆轨道半径OA、OB、OC的转动追及来分析.

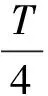
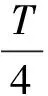
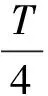
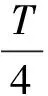
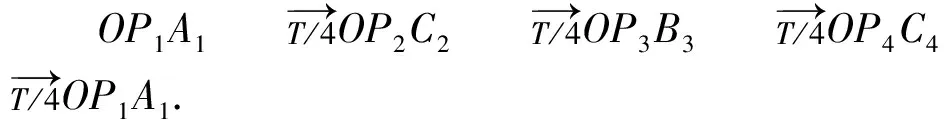
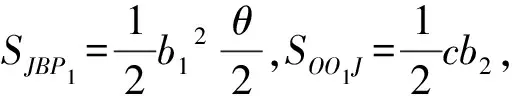
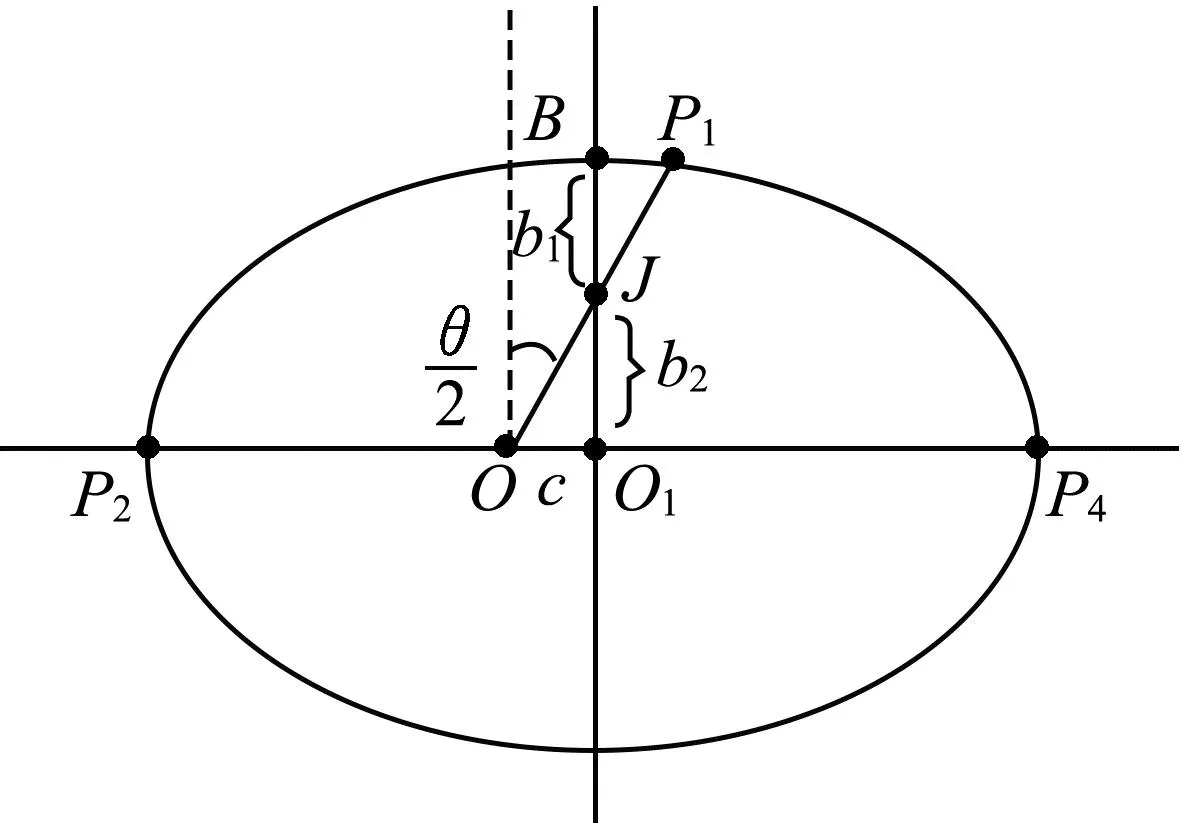
图4 椭圆轨道

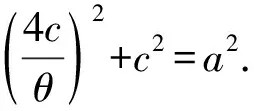
解析3：极坐标方程分析.

天体做圆锥曲线运动的问题研究中,极坐标系圆锥曲线方程是常用的数学方法．

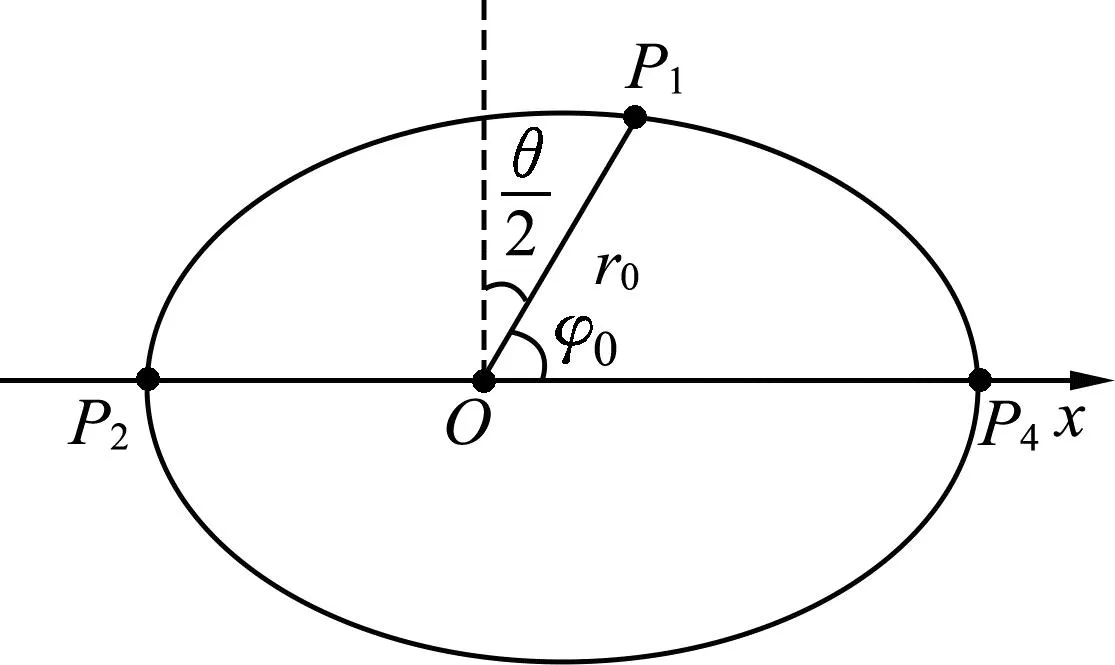
图5 椭圆的极坐标表示

椭圆运动时间分析.根据角速度

得到转动微小角度dφ的时间为

考虑到本题情境e为小量,可近似表示为

卫星运动过程P4→P1：矢径转动角度为φ0,经历时间T/4,有

卫星运动过程P1→P2：矢径转动φ0→π,经历时间T/4,有

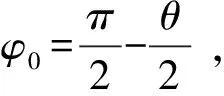
从上述对椭圆轨道卫星相对于赤道的漂移过程分析与解答过程不难体会到,给出的3种解法中除了必要的运动分析与小量近似之外,所用到的物理规律只有开普勒第二定律.该问题将开普勒第二定律与椭圆的性质结合得如此之紧密,需要具备较高的物理分析能力和相应的数学方法运用的能力．在物理培优教学过程中,不同板块的物理内容,对数学的要求也是有一定的针对性,在天体运动这一板块,对圆锥曲线,特别是椭圆的性质运用的要求极高．加之天体运动在中学生物理竞赛中又是不折不扣的高频考点,在教学过程可选用此类探究性的问题,以培养学生熟练运用数学知识研究物理问题的数理融合能力．