小球在非固定凹槽中的下滑时间研究

陈 胜 杨烁涓 杨 庆

(1. 电子科技大学,四川 成都 611731; 2. 邵东市城区第三初级中学,湖南 邵阳 422899;3. 成都七中,四川 成都 610042)

球槽模型中,如果轨道固定不动,小球沿旋轮线轨道从端点到最低点的下滑时间最短,并与自身质量无关.然而,当接触面光滑且凹槽形状较为复杂时,例如2023年新课标Ⅰ卷物理第15题考查小球在椭圆形轨道中的相对运动,小球的运动性质将受自身质量、凹槽质量及凹槽形状等因素的影响,呈现出较为特殊的动力学现象.

1 模型及问题

例1.如图1所示,在光滑水平地面上放置一个质量为M的匀质光滑凹槽,其轨道形状函数为y=

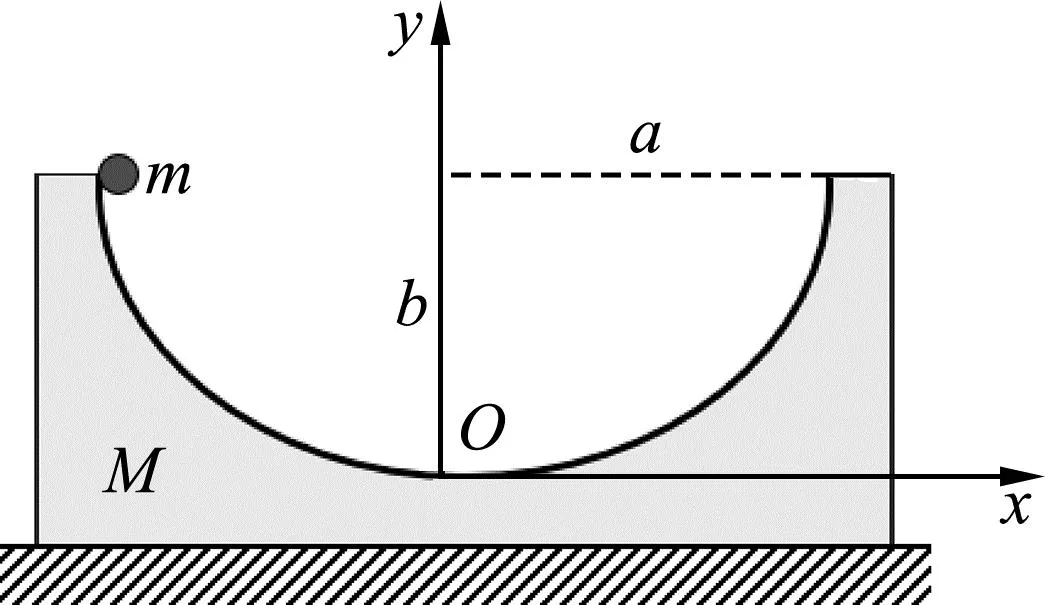
图1 球槽模型示意图f(x),凹槽的开口宽度为2a,深度为b.质量为m的小球从轨道左端点由静止开始下滑,整个过程凹槽不翻转,重力加速度为g,求小球下滑到凹槽最低点的时间.

2 公式推导

以凹槽最低点为原点,建立非惯性坐标系xOy,其中x和y为小球相对于槽的位置,取向右为速度和位移正方向.vm和vM分别为小球和凹槽相对于地面的速度,xm和xM分别为小球和凹槽相对地面的位移.

小球下降高度b-y时,根据能量守恒,小球的重力势能转化为小球和凹槽的动能,可得

(1)

由于地面光滑,小球凹槽系统在水平方向上的动量守恒,

mvx+MvM=0.

(2)

将式(2)对时间进行积分(等价于质心不变定理)

mxm+MxM=0.

(3)

小球和凹槽的位移在运动过程中始终遵从几何关系

a+xm-xM=x.

(4)

由式(3)(4)得(1+m/M)xm=x-a,于是小球绝对速度的竖直分量为

(5)

联立式(1)～(5),小球在(x,y)处的绝对速度的水平分量为

(6)

小球相对于凹槽的水平速度vx′为

(7)

于是小球从左端点到达凹槽最低点的时间为

(8)

等价于

其中y=f(x)与x=f-1(y)互为反函数.

3 数值结果与分析

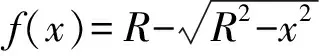
3.1 轨道一定

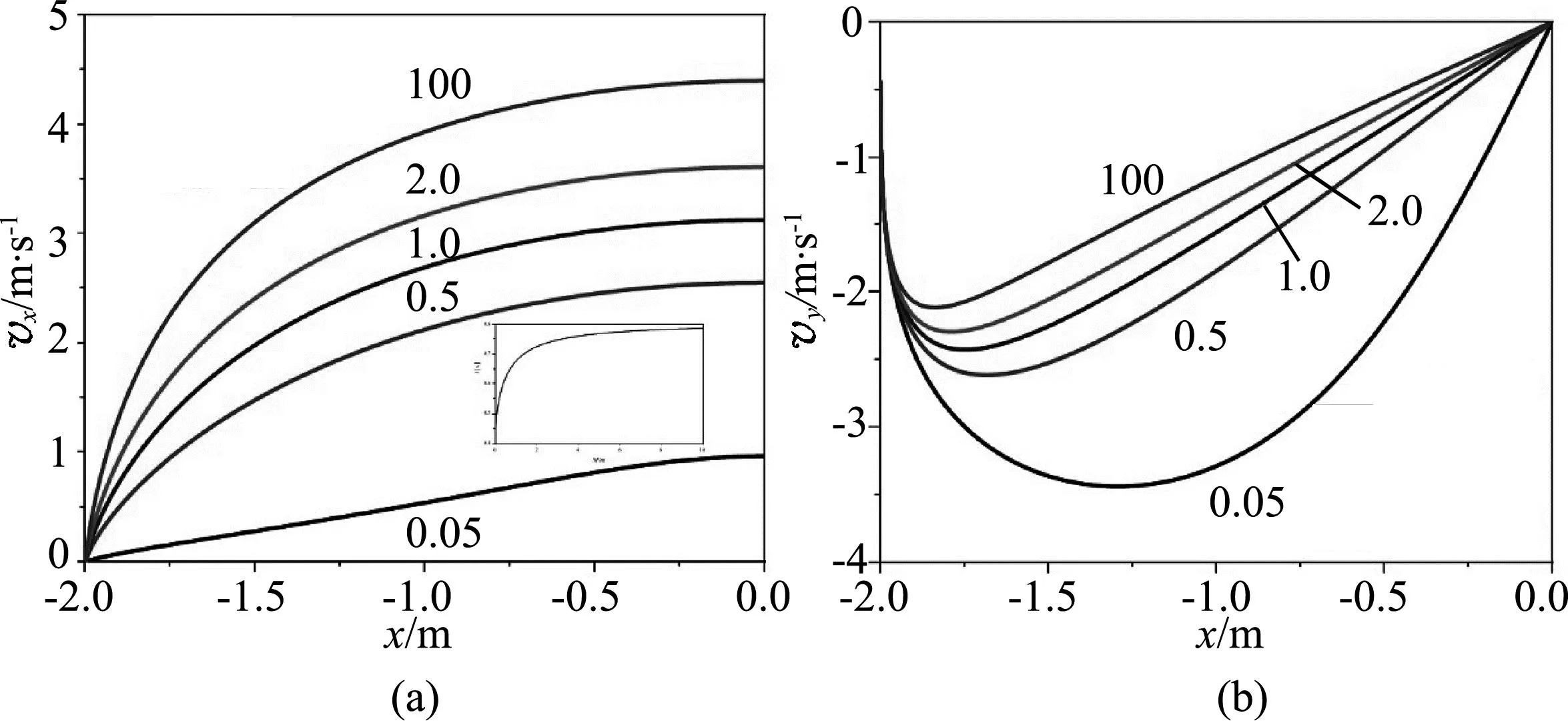
图2 小球速度分量与其在凹槽中位置的关系曲线(a) vx-x; (b) vy-x.[图中小框中为t-M/m曲线,与图3(b)一致]

随着M/m的增大,vx-x曲线逆时针旋转,小球到达凹槽相同位置的速度增大.曲线之间间距逐渐减小,对应的下滑时间t收敛于凹槽固定时小球从端点运动到最低点的时间.然而,从t-M/m图可知,M/m增大将使得vx和t同时增加,于是小球速度越大,并不一定导致下滑时间更短.这是因为小球与凹槽处于相对运动,小球在凹槽中的运动时间取决于小球与凹槽之间的速度差值(相对速度),而与小球的绝对速度无关.此外,由动量守恒定律可知,当小球向右运动时,凹槽将向左运动,小球相对凹槽的速度将增加,从而减少了小球到达相同位置所需的时间.

当小球与凹槽的质量相差不大时,它们之间的相互作用将显著影响小球的运动.一般来说,M/m越大,凹槽对小球的约束力和反作用力也较大,导致小球“慢”下来,做加速度减小的加速运动.同时vx增大vM减小,两者之间的相对速度减小,小球的下滑时间增加,具体时间由M/m比值决定,而其中M起主要影响.结合vy-x图进行分析,同一位置处的vy逐渐减小,与vx的定性关系完全相反,并且vy-x曲线呈现下凹形状,小球竖直方向经历先加速再减速的过程,且vy的最大值随M/m的增大而减小,速度发生转折的x值也更靠近端点,这两个因素都使得小球下滑时间增加.

3.2 质量比一定

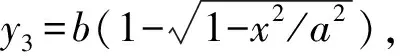
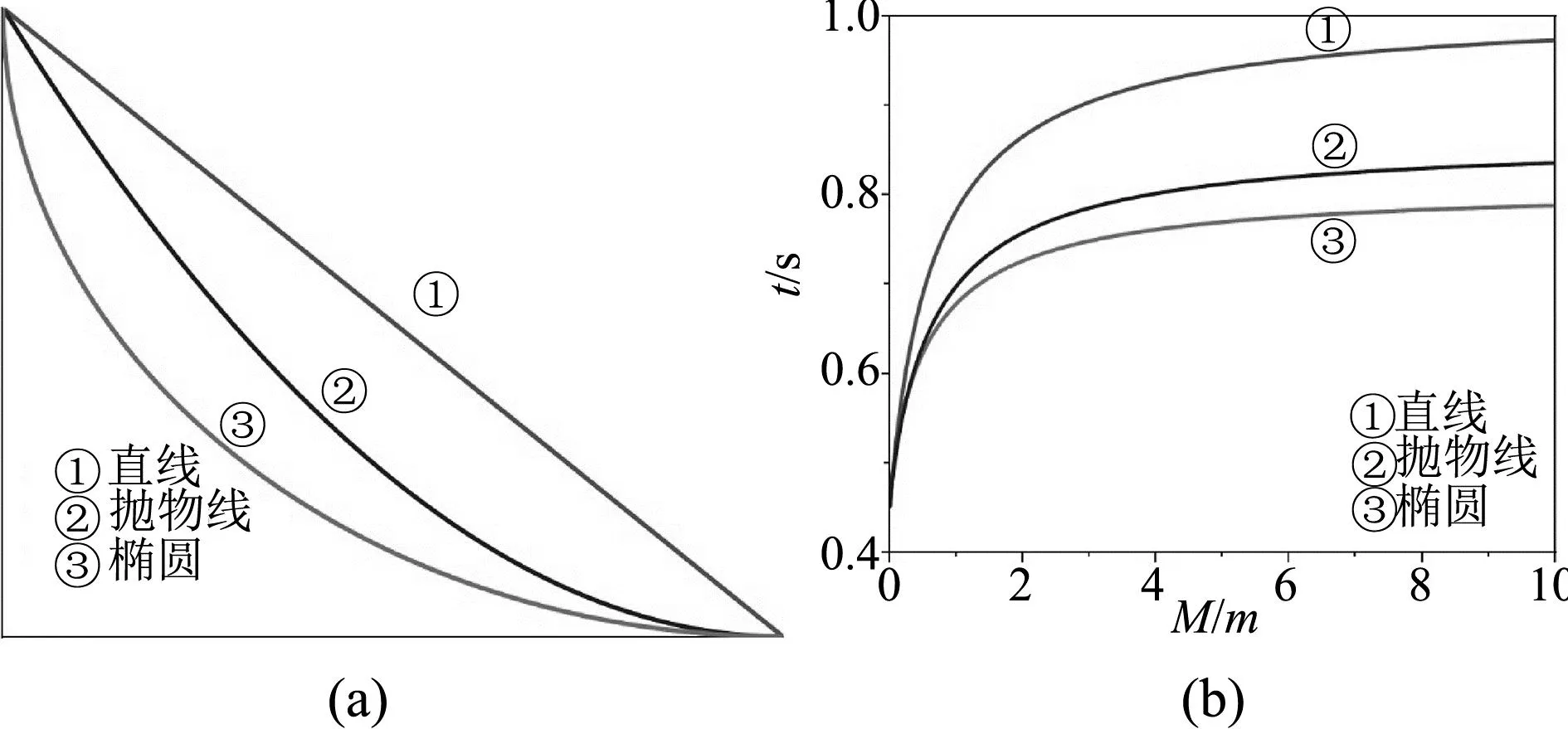
图3 (a) 3种不同轨道形状图及(b)下滑时间和M/m的关系曲线

4 总结与反思

本文基于一道高考物理压轴题进行拓展分析,探究了具有较特殊形状的球槽模型中的相对运动,并利用公式和图像法得出：凹槽和小球的质量比越大,凹槽轨道的形状越弯曲,小球从端点下滑到轨道最低点的时间就越短.因此,教师在教学中不能仅局限于经典结构,还应该学会拓展思维,延伸模型的应用范围,并掌握问题背后的物理原理和机制,以进行合理的分析.同时教师不仅要教导学生解题步骤,还可以借助作图软件或实验等手段,让学生直观感受到相对运动背后的物理图像,以加深他们对此物理概念的理解.只有这样,学生才能拥有更广泛的认知,更好地理解答案的来源,从而提高物理学习的效果和质量.