基于三维点云数据的焊缝识别方法研究

唐国寅,温秀兰,赵 岚,李国成,陆大为

(1. 南京工程学院自动化学院, 江苏 南京 211167;2. 南京矽景自动化技术有限公司, 江苏 南京 210012)

随着计算机视觉和人工智能技术的快速发展,焊接过程中的焊缝识别已经逐渐实现了自动化[1-3].点云技术作为一种新兴且重要的三维数据获取与处理方式,正被越来越多地应用于焊缝识别领域.点云技术可以将复杂的物体表面转换为由大量点构成的点云模型,为焊缝识别提供了更加全面、精确的三维信息[4-6].在不断探索点云技术在焊缝识别中应用的同时,如何有效地对点云进行处理和分析以达到高效、准确的焊缝识别也是当前研究的重要方向之一[7-8].文献[9]基于图像法自主研发了一款焊缝检测系统,该系统精度高、性价比高、抗干扰能力强,适用于V型、U型焊缝.但实际应用中对光源要求高,有一定局限性.文献[10]提出了一种基于纹理特征差异的方法,该方法能准确定位焊缝区域并获取中心点信息,但是在焊接位置的确定过程中,强烈的弧光和电弧噪声会对结果产生负面影响,使得准确快速定位焊缝区域变得困难,直接影响焊接的质量和效率.为了解决工业机器人焊接不稳定、工作效率不高、质量低和易受弧光影响的问题,本文提出一种基于三维点云数据的焊缝识别方法.

1 焊接机器人系统设计

为实现高效、稳定的焊缝识别,本文搭建一个基于3D视觉的焊接机器人系统,如图1所示.系统由机器人控制箱、UR5e、焊枪、Zivid相机、相机支架和上位机组成.焊枪固定安装在UR5e机械臂的末端,相机与机械臂采取眼在手外的方式安装.通过对机器人进行工具坐标系的标定和机器人手眼标定,可以分别获取机器人基坐标系与焊枪坐标系之间的转换关系以及机器人基坐标系与相机坐标系之间的转换关系.系统的整体实现流程为:1) 由Zivid相机获取整个目标表面的点云数据;2) 在上位机中对原始点云进行处理,获得焊缝轨迹并发送给机器人控制箱;3) 由机器人控制箱控制机器人本体及焊枪实现焊接.

图1 焊接机器人系统组成图

2 点云处理算法

2.1 点云滤波

通过Zivid相机获得的原始点云数据包含焊缝以及周围环境的深度信息,且每次拍摄的点云都包含2 234 000个点,数量级较大.因此,需要通过点云滤波处理去除原始数据中的噪声,并在不丢失焊缝特征信息的情况下完成下采样,以提高焊缝识别精度、加快焊缝识别速度.

半径滤波可以快速剔除离群点,并且能保留点云的基本形态结构,使点云的整体形态不会发生大的变化.对于半径滤波处理后的点云,其点的数量依然较多,还需进行点云下采样.体素滤波的优势在于简单快速,能够有效地对点云进行平滑和下采样,同时保留了点云数据的整体特征.体素滤波公式为:

(1)

2.2 点云平面拟合

常用的平面拟合方法有随机抽样一致(random sample consensus,RANSAC)算法、最小二乘法、主成分分析法等.其中RANSAC算法具有鲁棒性高、不易受离群点干扰等优点,但耗时较长.为减少RANSAC算法的运行时间,本文提出一种改进RANSAC算法,具体步骤为:

1) 从点云数据集θ中任意选择几点组成最小样本子集Φ,本文选择最小样本子集Φ包含3个点;

2) 采用最小二乘法获得选定子集Φ对应的平面模型参数;

3) 计算剩余的数据集中每个点到拟合平面的欧式距离d,如果点到拟合平面的距离d小于预定义的距离阈值D,则将其视为内点,否则将其视为外点;

4) 统计内点的数量,作为平面模型的质量度量,采用k最近领域搜索找到最小样本子集Φ中每个点周围的g个点,判断g个点中满足内点条件的数量,并求出最小样本子集Φ周围满足内点条件数量的总和,如果总和小于预定义的数量阈值U,则直接进入下一次循环;

5) 重复步骤1)—4)R次,从所有迭代中选择具有最大内点数量的平面模型Ax+By+Cz+D=0作为最优平面模型,并利用该平面模型重新拟合整个点云数据集,以得到更精确的参数估计.

改进RANSAC算法通过迭代次数R和样本污染率ε来影响算法的鲁棒性和准确性.迭代次数计算式为:

R=lg(1-P)/lg(1-(1-ε)h)

(2)

式中:ε为样本污染率,表示数据集中可能存在的异常值比例;P为置信概率,表示期望以一定置信度找到符合模型的内点;h为初始化模型参数的数量.

2.3 焊缝特征提取算法

为了提取焊缝特征点,需要进行以下步骤:

1) 设定一个距离阈值系数T,该系数将有助于确定异常点;

2) 去除拟合平面上的所有内点,从而得到凹槽点云;

3) 计算凹槽点云中每个点到拟合平面之间的欧式距离αi(i=1,2,3,…,e,e为凹槽点云中点的数量),公式为:

(3)

4) 从αi中找到最大值αmax,其代表凹槽点云中与拟合平面相距最远的点的距离;

5) 利用αmax和设定的阈值系数T来确定焊缝特征点,具体而言就是筛选出αi大于αmaxT的点,并将它们确定为焊缝的特征点.

通过这种方法能够自动识别出与最佳拟合平面相距较远的点,从而找到可能存在的焊缝特征点,提高数据分析的效率,准确地定位和识别出具有重要结构意义的特征点.需要注意的是,选择适当的阈值系数T非常重要,它将直接影响到最终所识别的焊缝特征点数量和质量.因此,在实际应用中需要根据具体情况进行调整和优化,以获得最佳结果.

2.4 路径规划

通过焊缝特征提取算法获得的特征点数量通常非常庞大,且分布密度不均匀,需要对焊缝特征点进行一系列处理和转换.

本文采用二次多项式拟合方法对焊缝特征点集进行空间曲线拟合,以获得平滑而连续的焊缝路径.曲线拟合后还需均匀地从曲线上取点,沿曲线等距选取焊接点,获得一个规范化的路径,使机器人能够顺利地按照该路径进行焊接操作.

设曲线的参数化形式为:

(4)

式中:t为参数;β(t)、χ(t)、γ(t)分别为x、y、z关于参数t的二次多项式函数.

设代价函数为:

(5)

式中:n为焊缝特征点的数量;(xs,ys,zs)为第s个焊缝特征点的坐标;ts为s点对应的参数值.

采用最小二乘法求代价函数J最小时对应的a、b、c、f、j、k、u、v、w,便可得到拟合的二次多项式参数化曲线.

3 试验结果

本试验选择铝合金材质的V型直线焊缝,焊件长100 mm,宽80 mm,厚8 mm,坡口为60°,坡深为4 mm,焊缝宽8 mm.图2为焊件原始点云图,共2 234 000个点.根据实验室Zivid相机获得的点云质量,设定样本污染率ε为0.1,置信概率P=0.99,平面模型参数h=3.

图2 直线V型焊件原始点云图

图3为原始点云经过半径滤波、体素滤波后的点云.图3(b)共8 947个点,能够清晰看到噪声基本被剔除,在保留点云整体特征的情况下降低了点云的密度和数量.

(a) 半径滤波

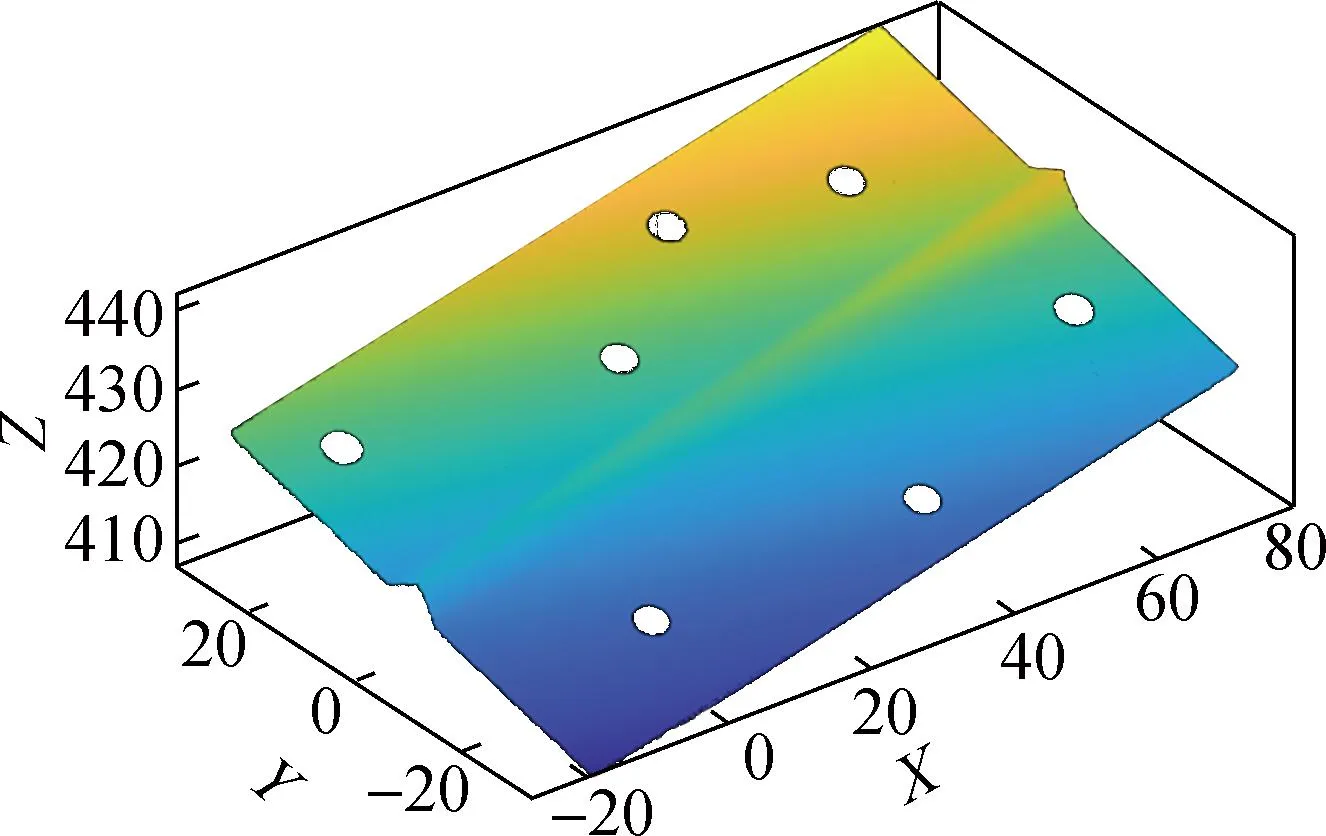
图4为改进RANSAC算法平面拟合效果图.为充分验证本文改进RANSAC算法的优越性,利用传统RANSAC算法与本文改进RANSAC算法对点云进行平面拟合,绘制两种算法对应的点到平面距离分布图,结果见图5.由图5可见,改进RANSAC算法点到平面的距离的平均值为0.615 mm,而传统RANSAC算法点到平面的距离的平均值为0.697 mm,改进RANSAC算法相较于传统RANSAC算法平面拟合精度提高了11.8%.进一步计算改进RANSAC算法点到平面距离的标准差为0.421 mm,运行时间为0.014 s,而传统RANSAC算法点到平面距离的标准差为0.701 mm,运行时间为0.322 s,改进RANSAC算法相较于传统RANSAC算法点到平面距离的标准差减小了0.280 mm,运行时间缩短了0.308 s.试验结果表明本文改进RANSAC算法相较于传统RANSAC算法具有更好的稳定性和更快的拟合速度.

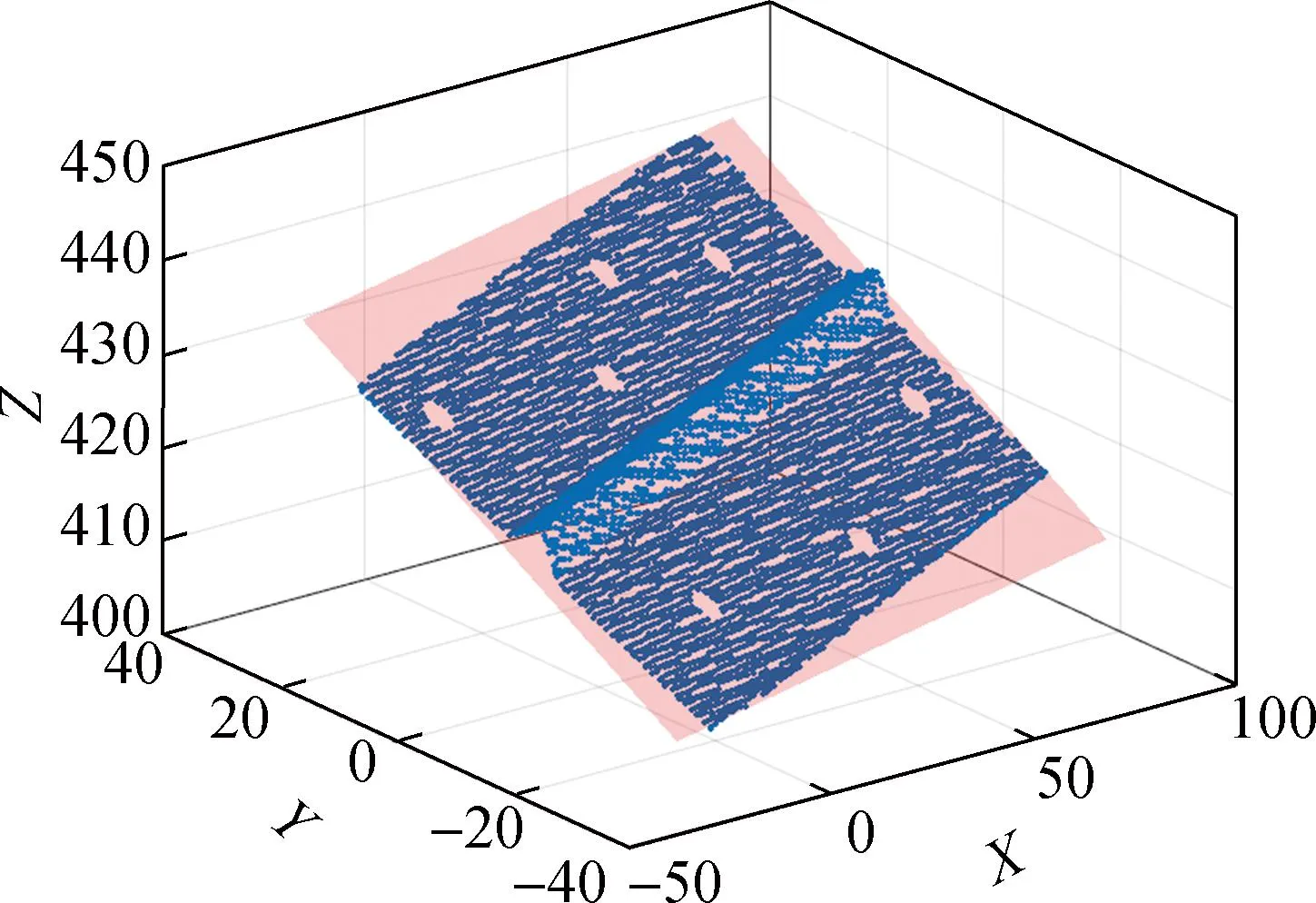
图4 改进RANSAC算法平面拟合效果图

图5 点到平面距离分布图

本文的焊缝特征提取算法设定阈值系数T=0.95,共提取到181个焊缝特征点,具体结果如图6所示.由图6的焊缝特征点可见,较为完整地提取出了整个焊缝,且焊缝特征点分布均匀,无大范围空隙,验证了本文焊缝特征提取算法的有效性.

图6 焊缝特征点提取示意图

焊缝特征点曲线拟合如图7所示.由图7可见,181个特征点到拟合曲线距离的平均差为0.219 mm,标准差为0.146 mm,运行时间为0.008 s,能够满足焊接的精度和速度要求.

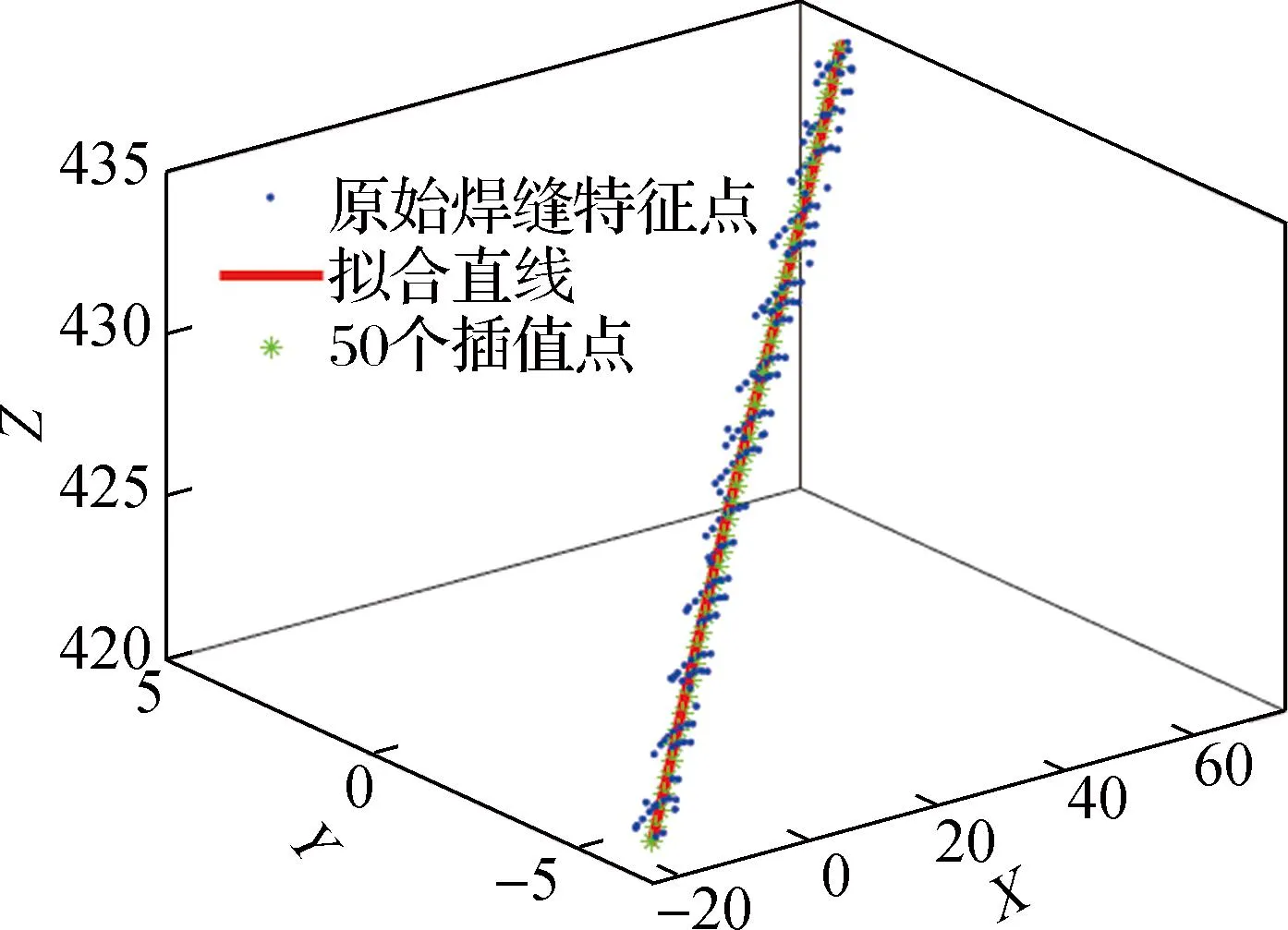
图7 焊缝特征点曲线拟合图

4 结语

针对工业机器人焊接不稳定、工作效率不高、质量低和易受弧光影响的问题,本文搭建基于3D视觉的焊接机器人系统,并提出一种改进RANSAC算法.试验结果表明,本文改进的RANSAC算法相较于传统RANSAC算法点到平面距离的标准差减小了0.280 mm,运行时间缩短了0.308 s,具有较好的识别精度和运行速度,能够在实际焊接中推广和应用,但对于多平面相交的焊缝识别精度还有待提升.