仿生蝙蝠扑翼飞行器设计及气动特性分析
陈国军,林羊龙,陈 巍,郭铁铮
(南京工程学院工业中心/创新创业学院, 江苏 南京 211167)
随着仿生理论、材料科学、自动控制等相关学科的发展,仿生扑翼飞行器已成为当前学术研究的热点.1998年,美国加利福利亚理工学院研制了一种仿生蝙蝠扑翼飞行器Microbat,其翼展15~20 cm,扑翼频率20~30 Hz,重量12.5 g,是世界上第一架可以持续飞行的微型扑翼飞行器[1];2012年,布朗大学研制了一款仿生蝙蝠翅膀,其有7关节并由3个电机利用绳轮驱动方式控制翅膀形态[2];2018年,德国FESTO公司制造了仿生蝙蝠BionicFlyingFox,其翼展228 cm,体长87 cm,重量仅580 g,翅翼膜具有轻、薄、高韧性的特点,在保证弹性的同时也能够满足飞行过程中的鲁棒性要求[3].
当前飞行器气动特性分析主要为静态分析,而动态气动特性分析具有更高的数据参考价值.本文设计一种翅翼扑动及折叠的仿生蝙蝠扑翼飞行器,对其翅翼扑动驱动及折叠机构分别建立数学模型,运用UG软件进行三维建模后,采用ADAMS-XFlow联合仿真的方法,利用ADAMS软件对模型进行运动学分析,得出仿生蝙蝠扑翼飞行器翅翼扑动角度幅值及翅翼折叠率,实现模型运动状态下的空气动力学仿真,分析其在不同翼型、不同来流流速及不同扑动频率下的各项飞行数据,根据仿真结果选择最佳飞行控制策略,为仿蝙蝠扑翼飞行器设计及试验提供理论基础.
1 仿生蝙蝠扑翼飞行器结构设计与运动学仿真
1.1 蝙蝠仿生飞行姿态研究
蝙蝠作为自然界高机动性飞行的代表,国内外学者对其空气动力学及运动学展开了研究,文献[4]通过粒子图像测速技术对其空气动力学、运动学及飞行形态学进行研究,但缺乏蝙蝠翅膀的运动及形状对其飞行空气动力学的影响;文献[2]通过调节运动学参数得出蝙蝠在扑翼过程抬升阶段通过折叠翅翼可以有效增加净升力,但由于仅设计单侧翅翼,未获得两侧翅翼同时扑动对整体气动特性及飞行效果的影响.根据蝙蝠扑翼飞行姿态及相关研究,归纳出蝙蝠飞行时翅翼的扑动整体流程为展开—下扑—收缩—抬升(见图1),仿生蝙蝠扑翼飞行器在结构设计时应使翅翼能够实现扑翼与折叠功能.
1.2 结构设计
1.2.1 驱动机构
本文设计的仿生蝙蝠扑翼飞行器采用空间曲柄摇杆机构作为驱动机构,如图2所示.该机构的自由度为:

图2 空间曲柄摇杆机构运动简图
F=3n-2FL-FH
(1)
机构单侧具有曲柄、连杆和摇杆3个构件、2个旋转副和2个球面副.将机构数n=3,低副数FL=4,高副数FH=0代入式(1),得到整体机构自由度F=1.图2中:以扑翼飞行器机身切向为X轴,飞行器前方为Y轴,竖直上方为Z轴,O为原点,建立三维坐标系;L1为曲柄旋转中心点A与摇杆旋转中心D在X轴的投影距离;L2为曲柄旋转中心A与摇杆旋转中心点D在Z轴的投影距离;L3为曲柄AB的长度;L4为连杆BC的长度;L5为摇杆CD的长度;α为输入曲柄旋转角度;β为输出摇杆旋转角度;B点的坐标为B(L1,L3cosα,L3sinα);C点的坐标为C(L5cosβ,0,L2+L5sinβ);L4为连杆BC的长度.
驱动机构运动方程为:
(L2+L5sinβ-L3sinα)2
(2)
根据机身结构布置及传动件长度要求,设L1=0.8 mm;根据整体外形尺寸要求,设L2=25 mm;摇杆长度与折叠机构各连杆长度相关,设L5=5.5 mm;当α=90°时,β达到最大值βmax,当α=270°时,β达到最小值βmin.因此,本文取α=90°时βmax=65°,α=270°时βmin=-40°,两组数据计算可得L3=4.17 mm,L4=25.86 mm.
1.2.2 折叠机构
本文设计的仿生蝙蝠扑翼飞行器采用滑块六连杆机构作为翅翼折叠机构,如图3所示,机构单侧具有5个构件(1个滑块和4个连杆)、6个旋转副和1个滑动副,将n=5、FL=7、FH=0代入式(1),得到整体折叠机构自由度F=1.以扑翼飞行器机身切向为X轴,飞行器前方为Y轴,竖直上方为Z轴,O为原点,建立三维坐标系,l为O到滑块中心点A的距离,m为A到连杆4支点E的距离,L1′为A到连杆1及连杆4交点F的距离,L4′为E到F的距离,Q1、Q2、Q3、Q4分别为连杆1、2、3、4与X轴夹角.
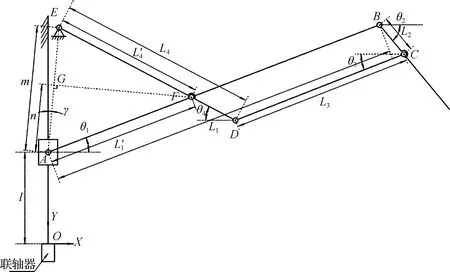
图3 平面六连杆机构运动简图
E点坐标为E(4.3,85),利用平面机构运动矢量封闭方程法将O、A、B、C、D、E在X、Y轴的投影表示为:
(3)
确定各连杆长度及L1与L4相交位置,即L{L1,L2,L3,L4,L1′,L4′}均已知,则通过输入l可得AE与OA的夹角γ,进一步可得m的长度,得出θ1与θ4,各参数关系式为:
(4)
将求得的θ1、θ4代入式(3),求得θ{θ1,θ2,θ3,θ4}
与输入l的关系.将数据导入Matlab进行求解计算,取C点X轴坐标投影变化范围作为翅翼折叠效果参考,令lmin=11 mm,lmax=66 mm,可求得Cxmin=126.053 8 mm,Cxmax=158.077 6 mm.
1.2.3 三维模型构建
运用UG软件按照驱动机构及折叠机构中所求参数对各杆件进行建模.扑翼机构由无刷电机输入,经过二级齿轮减速后输出至曲柄,通过空间曲柄摇杆机构实现摇杆即整个翅翼的扑动.由于两侧曲柄转动由同一个齿轮输出,机构磨损少,整体扑翼飞行器重量得以降低.此外,两侧曲柄转动由同一个齿轮输出使两侧翅翼扑动不存在相位差,相较于单曲柄双摇杆机构而言,空间曲柄摇杆机构对称性好,整体飞行器气动性能得以提升,如图4所示.

图4 扑翼机构示意图
折叠机构由行星减速空心杯电机输入,通过联轴器将电机与微型丝杆连接,丝杆螺母与丝杆配合,实现将电机的旋转输出转化为丝杆螺母的平移运动,从而改变折叠机构中的参数l,实现折叠机构的折叠运动,如图5所示.
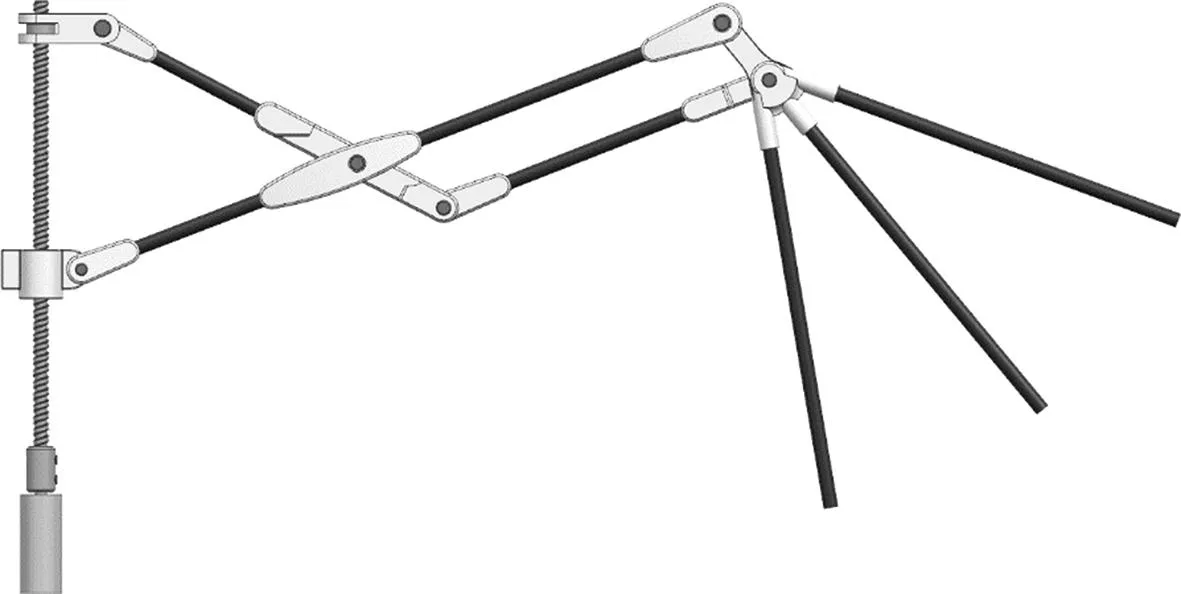
图5 折叠机构示意图
1.3 运动学仿真
将三维模型导入ADAMS软件赋予约束、运动副及驱动,对其进行运动学仿真,得到如图6所示的扑动角度幅值变化曲线.

图6 扑动机构在ADAMS软件中扑动角度幅值变化曲线
ADAMS仿真结果与Matlab求解得到的曲柄摇杆角度曲线吻合,扑翼机构模型与数学模型分析结果对应,扑翼机构输出摇杆旋转角度最大值为βmax=67.8°,最小值为βmin=-40.3°,即扑翼角度运动幅值为108.1°.
将所设计折叠机构导入UG模型进行运动仿真,得到如图7所示的翅翼折叠状态图及翅翼展开状态图.

(a) 翅翼折叠状态
在翅翼完全展开时覆盖独立的内翼及外翼,利用折叠后的重复面积,根据投影面积可得翅翼完全展开面积为23 419.71 mm2,折叠后面积为18 586.95 mm2,折叠率约为20.60%.
2 仿生蝙蝠扑翼飞行器气动特性仿真与分析
2.1 气动特性仿真
目前,扑翼飞行器常用翼型主要有矩形翼、半椭圆翼、齐默曼翼和反齐默曼翼.本文选用矩形翼及半椭圆翼进行对比试验.运用XFlow作为仿真软件研究不同翼型、空气来流流速及扑动频率对扑翼飞行器气动特性的影响,通过2种不同的翼型(矩形翼、半椭圆翼)、5组不同的空气来流流速(1、2、3、4、5 m/s)及5组不同的扑动频率(0.5、1.0、1.5、2.0、2.5 Hz)进行试验数据对比.
在XFlow中设置计算域时,要在满足阻塞比要求的同时尽可能小,提高计算效率同时保证计算结果的可信性[5].本文设置计算域大小为0.75 m×0.75 m×0.75 m.由于模型在来流方向截面投影面积为0.005 3 m2,而计算域在来流方向截面投影面积为0.562 5 m2,故阻塞比为0.94%,满足阻塞比要求.设定流体材料为空气,流体密度1.225 kg/m3,流体温度15 ℃,动力黏度1.789 4×10-5Pa·s.采用近模型壁面精细算法,同时设定一个矩形精细领域以提高尾迹精度.仿真时间为4 s,帧频率为60 Hz,总帧数为240帧.
2.2 仿真结果分析
2.2.1 不同翼型的气动特性分析
文献[6]通过研究得到半椭圆翼气动特性相对较好、矩形翼气动特性相对较差的结论;文献[7]在扑翼飞行器平面形状对气动力的影响研究中表明,翼面迎角在扑翼升力系数增加中起决定作用.本文为研究不同翼型对扑翼过程中气动特性的影响,采用矩形翼及半椭圆翼两种翼型进行对比试验,扑动频率设为0.5 Hz,来流流速设为3 m/s.
矩形翼和半椭圆翼的扑翼弦向速度云图如图8所示.由图8可见,飞行过程中矩形翼上、下表面气流速度差较小,未产生明显速度差,无法形成压差及升力;半椭圆翼上表面气流速度明显高于下表面气流速度,产生较大气流速差,形成明显压差,产生较大升力.

(a) 矩形翼
将XFlow中解算完成的矩形翼及半椭圆翼的升力系数Cl及阻力系数Cd数据导出(见图9),平均升力系数和平均阻力系数如表1所示.由图9及表1可见,采用半椭圆翼能够有效提高升力系数、降低阻力系数,使阻力系数变化更加平稳,扑翼飞行器飞行状态更为稳定.

表1 不同翼型平均气动特性参数

图9 不同翼型升力系数与阻力系数变化曲线
2.2.2 不同来流流速的气动特性分析
为分析来流流速对扑翼飞行器气动特性的影响,在保持其他参数不变的情况下,分析不同来流流速(1、2、3、4、5 m/s)下升力、阻力系数的变化.图10为不同来流流速下的扑翼展向速度云图,其中左侧图为抬升阶段,右侧图为下扑阶段.
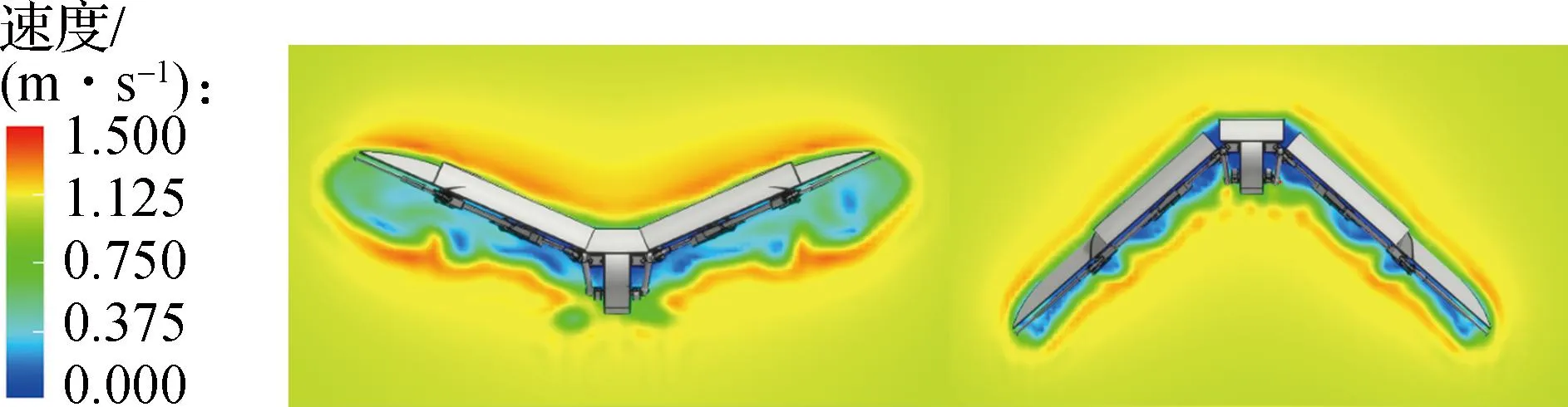
(a) 1 m/s来流流速
文献[8]通过设定运动方程实现翅翼上下扑动、绕翼展方向扭转、内外翼弯曲折叠功能,将模型导入XFlow后,给予位置方程及角度运动方程,实现扑翼飞行器的挥拍—扭转—弯曲折叠运动,表2为不同来流流速下平均升力系数及阻力系数.分析图10和表2数据可知,半椭圆翼型结构使得上表面气流速度大于下表面气流速度,形成气流速差,并随着来流流速的提升,气流速差范围扩张、速差略微增大.低风速环境下,扑翼运动过程及翼型上下表面气流速差带来的升力均相对明显;高风速环境下,高速气流使扑翼附近空气流动行迹紊乱,影响扑翼运动过程产生升力,同时也会使翼型表面涡流快速脱离,无法有效提供升力,因此,表2中的平均升力系数随来流流速提升呈先增大后减小趋势.
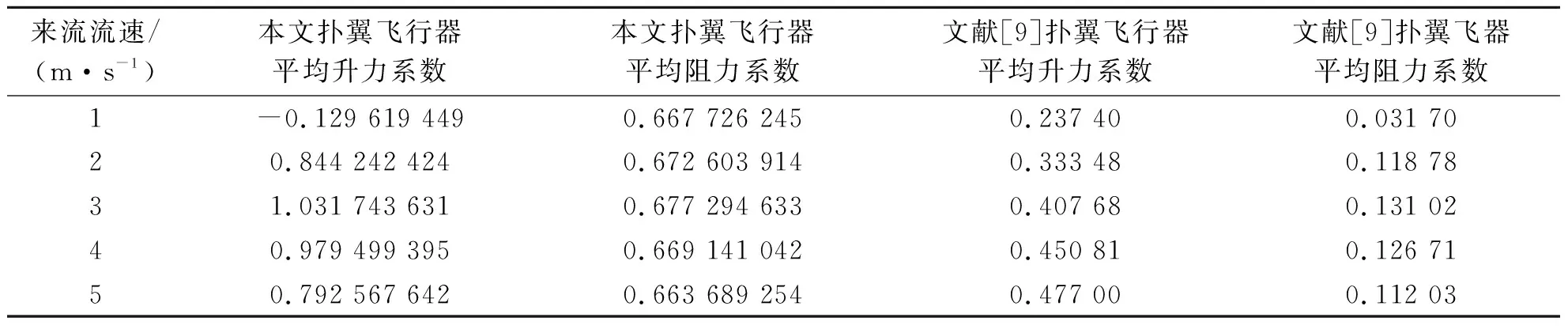
表2 不同来流流速平均气动特性参数
2.2.3 不同扑动频率的气动特性分析
为分析扑翼频率对扑翼飞行器气动特性的影响,在保持其他参数不变的情况下,分析0.5、1.0、1.5、2.0、2.5 Hz五组不同扑翼频率下升力、阻力系数的变化.图11为不同扑翼频率下升力系数变化曲线图,图12为阻力系数变化曲线图,表3为不同扑翼频率下平均升力系数及阻力系数.随着扑翼频率的增大,升力系数峰值变大,平均升力系数也逐步提升;由于扑翼过程中会产生部分推力,阻力系数逐渐减小,最终阻力系数<0.
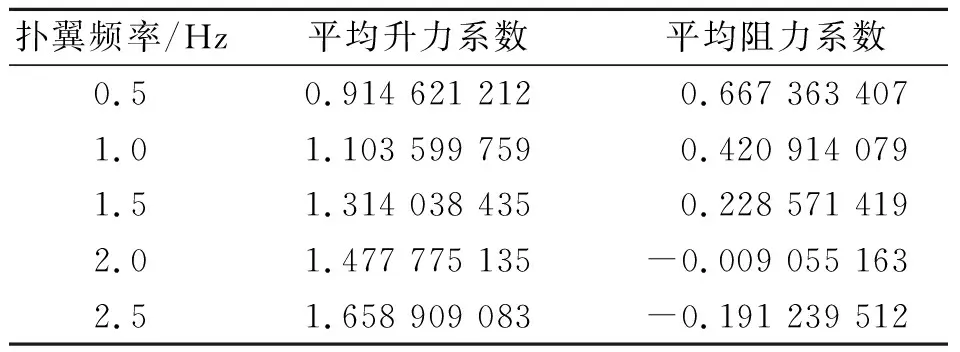
表3 不同扑动频率平均气动特性参数
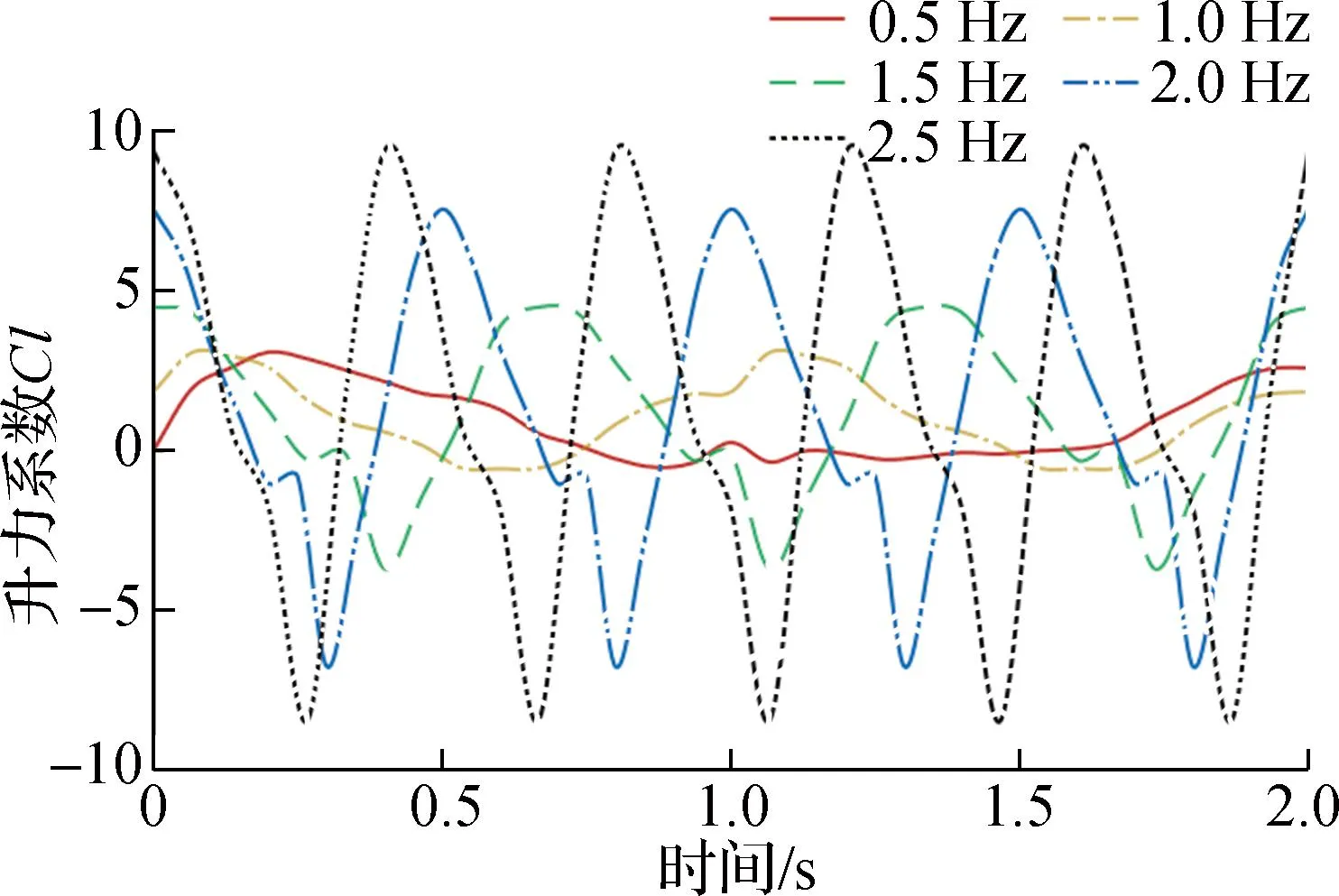
图11 不同扑动频率升力系数变化曲线图
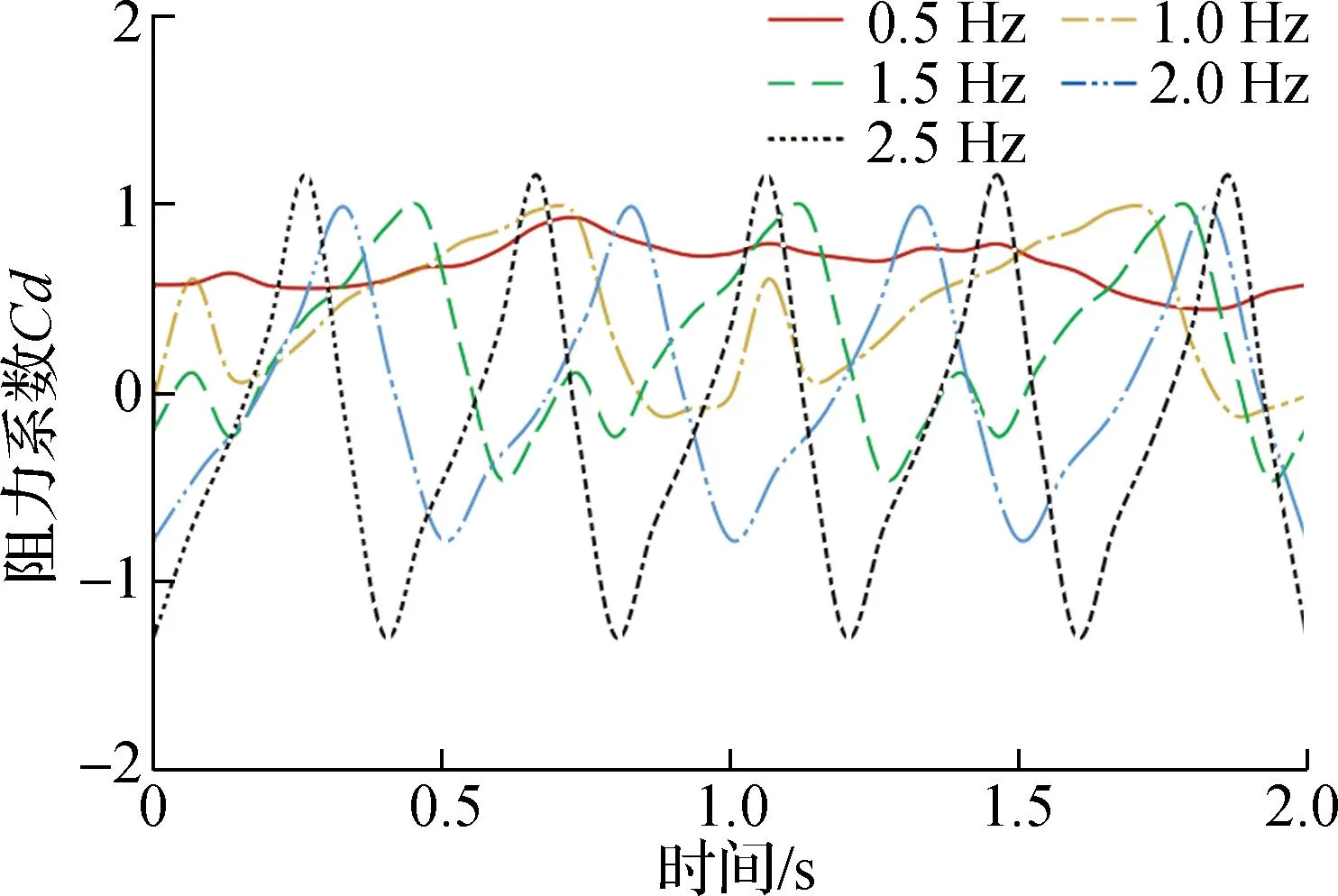
图12 不同扑动频率阻力系数变化曲线图
2.2.4 扑翼飞行器最优飞行控制策略
通过对仿生蝙蝠扑翼飞行器在不同翼型、不同来流速度以及不同扑动频率下的气动特性进行对比分析,可以得出本文设计的仿生蝙蝠扑翼飞行器的最优飞行控制策略:采用半椭圆翼获得更大的平均升力系数,更小的平均阻力系数,使飞行更加平稳;飞行速度控制较低速度范围约3 m/s,有利于半椭圆翼发挥翼面效应,获取较大升力;扑动频率控制在2 Hz,可获得最大升力峰值、较大平均升力和较小平均阻力,有利于获得更高的推进效率.
3 结语
本文设计一种仿生蝙蝠扑翼飞行器结构,通过数学模型对扑翼机构及折叠机构进行理论推导.利用UG软件实现三维建模,并通过ADAMS运动学仿真验证理论分析结果.采用ADAMS-XFlow联合仿真实现模型在预设运动状态下的空气动力学仿真,得到不同截面速度云图及平均升力系数、平均阻力系数等参数.通过分析不同翼型、不同来流流速及不同扑动频率下的各项飞行气动特性参数的数值大小及变化,分析各项条件对本文所设计的扑翼飞行器飞行性能的影响,为后续研究提供了相关的研究方法及仿真数据.

