考虑竖向荷载作用时液化土中高桩基础水平动阻抗分析

陈 正，陈习华，侯 靖，胡安峰

（1.浙江大学 建筑工程学院，浙江 杭州 310058；2.浙江省机电设计研究院有限公司，浙江 杭州 310051；3.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122）

0 引 言

高桩作为跨海桥梁、海上风机、石油钻井平台等海工结构常用基础，所处工作环境复杂，在受到多种竖向、水平向荷载耦合作用时仍有良好的抗震承载性能。目前，针对陆上完全埋入桩动力响应特性的研究较为丰富，基于Biot 饱和多孔介质理论、动力Winkler 模型开展的液化土中埋入桩振动特性的研究也有一定成果[1-3]。但针对复杂工况下液化土中高桩水平振动特性研究仍较为缺少。

高桩基础包含的上部自由段缺少侧向土体约束，其动力特性较陆上完全埋入桩有较大的差异。国内外开展的高桩动力响应研究比较有限。LEE 等[4]对弹性地基中受竖向荷载作用的部分埋入变截面桩自由振动特性开展研究，分析了自由段占比、桩周土参数等对桩基振动模态的影响。任青等[5-6]基于动力Winkler 模型，利用矩阵传递法求解单桩的竖向振动与水平向振动方程，后考虑桩间的相互作用，对部分埋入群桩的振动特性进行了深入研究；之后，将桩基视作多个子结构，考虑承台板对群桩阻抗的影响，研究承台厚度对群桩内力分布的影响。黄茂松等[7]采用动力Winkler 模型，对承受较大倾覆力矩的海上风机部分埋入群桩基础进行模拟，考虑基础阻抗作用，分析基础阻抗对海上风机共振特性的影响。付鹏[8]基于饱和多孔介质理论，对承受复杂荷载作用下的饱和土中高桩振动特性进行研究。以上研究在无液化土作用的工况下开展。东南沿海地区是我国地震的高发区域之一，分布广泛的海洋表层天然泥沙沉积物[9]在地震荷载作用下极易产生液化现象[10]，而现有液化场中高桩基础水平振动特性的研究较少。高桩基础工作环境复杂，不仅承受风力、波浪等水平荷载，竖向荷载也会对桩基的动力特性产生影响[2]，但基于饱和多孔介质理论的相关研究却少见考虑这一因素[3]。而桩周土体液化导致桩侧支护反力减小，竖向荷载又会增强这一因素对桩基力学特性的影响，因此有必要考虑竖向荷载。

利用数值模拟可以高效地研究复杂环境中桩-土耦合系统振动特性，但理论解析在对某些参数的分析上更方便。而考虑了土体竖向连续性的连续介质模型引入参数多，计算复杂，针对某些更复杂的工程应用不方便。因此文章基于Biot 饱和多孔介质理论，引入Novak 薄层法，研究液化场中高桩基础的水平振动特性，探讨液化土厚度、液化土密度、竖向轴力等因素对桩基动阻抗的影响。

1 计算模型及基本假定

桩土系统简化计算模型如图1 所示，表层液化土体视作无黏性不可压缩流体，底部土层为饱和两相多孔介质，桩基为弹性均质杆件。桩顶受到竖向荷载、水平简谐荷载、弯矩的耦合作用。桩体半径为r0，自上而下分为3 段，自由段桩长为H1，液化土中桩长为Lls，非液化土中桩长为Ls，地基土层厚度为L=Lls+Ls。

图1 桩土系统简化计算模型Fig.1 Simplified calculation model of pile-soil system

桩土系统引入以下假定：

（1）桩基为忽略剪切变形的圆形等截面一维Euler 梁，线黏弹性材质，为底部固定支撑的嵌岩桩；

（2）液化土视作无黏性不可压缩流体，在水平面上无限延伸，不考虑辐射阻尼影响与表面波影响，离桩身越远液化土振动越弱，直至为零，且忽略因外荷载作用导致的液化土初始扰动，液化土底面不发生竖向位移；

（3）饱和土为各向均质的黏弹性土，在水平荷载作用下仅产生径向、切向位移，忽略振动产生的土体竖向位移；

（4）桩-土接触面良好，桩与液化土、非液化土不产生振动脱开、滑移，接触面不透水，耦合体系振动为小变形。

1.1 液化土位移控制方程

由流体波动理论，可以得到柱坐标下的流体运动控制方程：

式中：φ(r,θ,z)eiωt为流体势函数，ω为激振圆频率。

1.2 非液化土位移控制方程

基于Biot 饱和多孔介质理论与Novak 薄层法，建立柱坐标下的饱和土水平振动控制方程：

ur，uθ分别代表土层的固相径向位移和切向位移；wr，wθ代表液相相对于固相的径向和切向位移；G为土体剪切模量，当土体阻尼为滞回阻尼时，G*=G(1 +2ζ i)，λ*=λ(1+2ζ i)，ζ 为土体滞回阻尼；α、M为土骨架和流体压缩性相关的Biot参数；ρ为土体密度，ρ=ρs(1 -n)+nρf，ρs与ρf分别为土颗粒、流体密度，n为土体孔隙率；m=ρf/n；bp=ρfg/kd，kd为桩周土体的渗透系数。

1.3 桩体振动控制方程

基于Euler 梁理论，由动力平衡条件，建立空气、液化土、饱和土中的以水平位移表示的振动控制方程：

式中：q i(i=1,2,s)分别为桩周液化土、空气、饱和土产生的动反力；(i=1,2,s)分别为液化土中段、空气段、饱和土中段桩基水平位移；、Ip、mp分别为桩体弹性模量、截面惯性矩、单位长度质量，当桩体存在滞回阻尼ζp时，=Ep(1 +2ζpi)。

1.4 桩土系统边界条件

液化土中段流体边界条件：

饱和土中段边界条件：

2 方程求解

2.1 空气中桩基振动

此时自由段桩基水平振动控制方程为：

该式通解可参考文献[8]。

用[S2(z)]=表示桩身的变形与受力。则得：

其中关系矩阵[X2(z)] 及参数亦可参考文献[8]。

2.2 桩-液化土相互作用

利用分离变量法，结合液化土速度势边界条件式（4），可以得到液化土作用在单位长度桩身上的动反力：

将式（8）代入式（3）可以得：

此时方程的解为：

式中：N11，N12，N13，N14为待定系数。

利用三角函数的正交性，结合桩-液化土的接触条件，可得：

将式（11）代入式（10），可得：

同理，可以得到液化土中桩段桩顶与桩底的位移变形的矩阵关系形式：

其中关系矩阵[X1(z)] 见式（14）：

2.3 桩-非液化饱和土相互作用

通过引入位移势函数，利用微分算子分解法、分离变量法和边界条件可以得到桩周土体动反力，可直接引用文献[11]，得到桩周土反力大小：

大黄素和黄芩苷联用对急性胰腺炎模型大鼠Akt/Nrf2通路的影响研究 …………………………………… 李慧艳等（13）：1754

代入式（3）可得方程通解：

与2.1 节方法类似，可得到非液化饱和土中桩段底部与桩顶的受力位移矩阵关系式，式中关系矩阵[Xs(z)] 与2.1 节类似。

2.4 桩顶阻抗求解

由桩体位移变形连续性，可得桩底与桩顶的位移、转角、弯矩、剪切力间的关系式：

由桩底位移条件式（5b），可得：

依次可得桩顶水平动阻抗、摇摆动阻抗：

可得无量纲化的水平动阻抗、摇摆动阻抗：

式中：Re 实部代表桩顶动刚度；Im 虚部代表桩体能量耗散的动阻尼。

3 合理性验证

为验证本文解的合理性，令Lls→0，P=0，此时模型退化为饱和土中不考虑竖向荷载的部分埋入桩水平振动解，同刘圆圆等[12]解作对比（图2）。计算参数如下：r0=0.5 m，L=20 m，H1=3 m，α=1，M=4.6 GPa，ν=0.25，n=0.375，ρf=1 000 kg/m3，ρs=2 700 kg/m3，ρp=2 500 kg/m3，G=12 MPa，Ep=30 GPa，kd=10-6m/s，ζ =0，ζp=0，引入无量纲频率。从图2 可以看出，本文解与无液化土中的部分埋入桩解结果完全吻合，说明了本文解的准确性。令H1=0 m，sL=0 m，ρls=1 000 kg/m3，该解可退化为水中圆柱梁的水平振动问题，将计算得到的桩顶阻抗同徐汉忠[13]解作对比（图3），由图3 可知本文退化解与水中圆柱梁解完全一致，再次验证本文解的合理性。

图2 文章退化解与刘圆圆解对比Fig.2 Comparison between degenerate solution and Liu’s solution

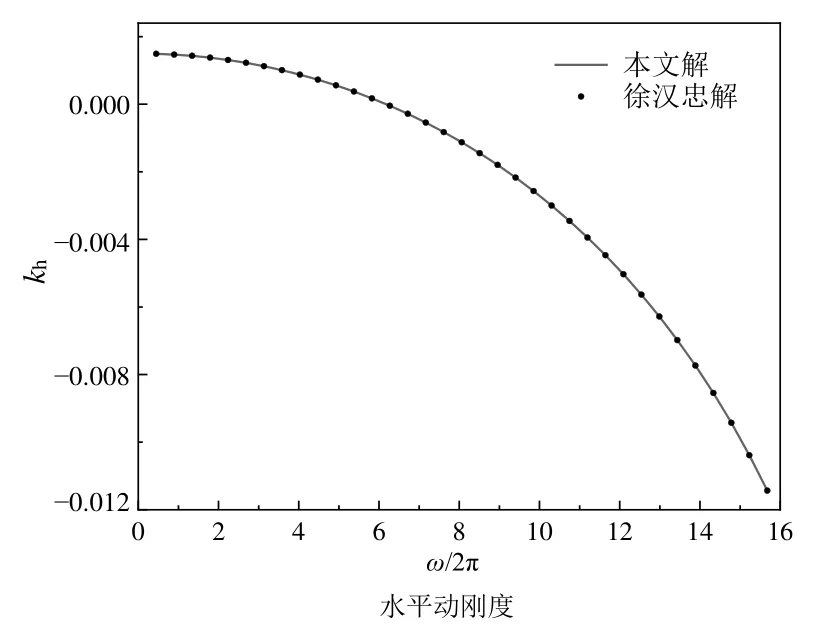
图3 文章退化解与徐汉忠解对比Fig.3 Comparison between degenerate solution and Xu’s solution

4 算例分析

分析中所采用的物理力学参数如下所示：H1=2 m，ν=0.3，n=0.4，ρf=1 000 kg/m3，ρs=2 700 kg/m3，ρls=1 900 kg/m3，G=10 MPa，Ep=25.5 GPa，kd=10-6m/s，ζ=0.05，ζp=0，桩顶竖向荷载=P500 kN。

首先研究表层液化土的厚度对高桩基础阻抗的影响。液化厚度Lls分别取Lls/L=0，0.05，0.1，0.2。Lls/L=0 时，退化为无液化地基中高桩基础桩顶动阻抗解。图4～5 反映了不同厚度液化土对高桩基础桩顶阻抗的影响。从图4～5 中可以看出，同一频率下，高桩桩顶动刚度随地表液化土厚度的增加而降低，液化土厚度越大，随着频率的增加，桩顶动刚度下降速度越快，越早进入负刚度。而动阻尼变化规律比较复杂：在低频激振下，动阻尼随着液化土厚度的增加而下降；在高频激振下，当液化厚度比例达0.2 时，桩顶动阻尼随激振频率变化的速度更快。

图4 液化土厚度对桩顶水平阻抗的影响Fig.4 Influence of thickness of liquefied soil on horizontal impedance of pile

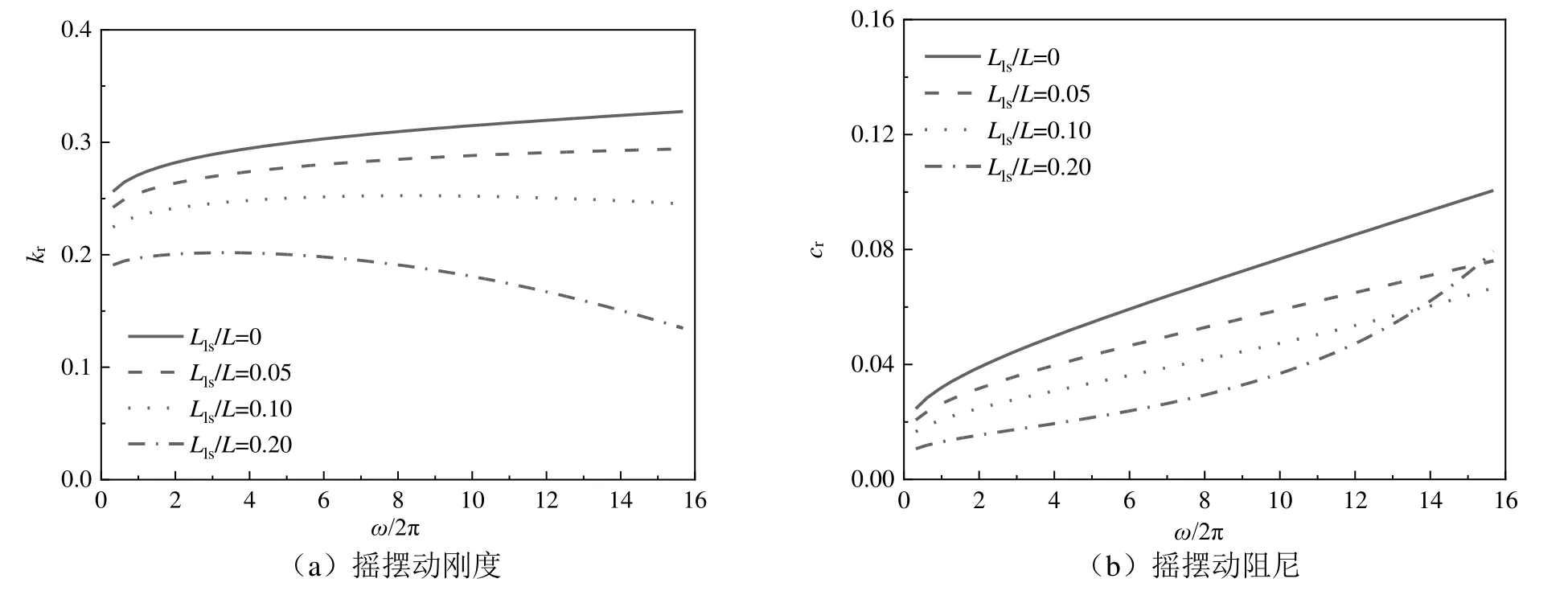
图5 液化土厚度对桩顶摇摆阻抗的影响Fig.5 Influence of thickness of liquefied soil on rocking impedance of pile

控制表层液化土厚度不变，流体密度分别取lsρ=2 500，2 200，1 900，1 600 kg/m3。图6～7 反映了液化土密度对高桩桩顶阻抗的影响。当激振频率小于4 Hz 时候，流体密度对桩基的动刚度影响不明显，随着频率进一步增大，高桩桩顶动刚度随密度的增大而减小。流体密度对于桩基动阻尼的影响则更小，只有在10 Hz 以上的频率激振作用下，液化土密度对桩基动阻尼的影响才会有所展现。

图6 液化土密度对桩顶水平阻抗的影响Fig.6 Influence of density of liquefied soil on horizontal impedance of pile

图7 液化土密度对桩顶摇摆阻抗的影响Fig.7 Influence of density of liquefied soil on rocking impedance of pile

控制表层液化土厚度不变，图8～9 反映了不同竖向荷载作用对高桩桩顶阻抗的影响，计算所用竖向荷载P大小分别取500，1 000，2 000，4 000 kN。从图8～9 中可以看出，桩顶动刚度随竖向荷载增大而减小，但减小程度有差异：竖向荷载对于水平动刚度影响不显著，对桩顶摇摆动刚度削弱程度更大；与之相反的是，竖向荷载对于桩基的动阻尼影响并不明显，几乎不影响能量在桩土系统中的耗散效率。刚度决定桩基抵抗变形的能力，在竖向荷载作用下，桩基刚度下降，且系统吸收能量的能力不变，桩基越容易发生失稳。这与实际地震中出现的桩基破坏规律类似，即桩顶竖向荷载越大，桩基越易变形，地震造成的桩基损毁程度更大，所以在高桩设计中需合理选取竖向荷载值。

图8 竖向荷载对桩顶水平阻抗的影响Fig.8 Influence of vertical load on horizontal impedance of pile

图9 竖向荷载对桩顶摇摆阻抗的影响Fig.9 Influence of vertical load on rocking impedance of pile

5 结 论

（1）高桩桩顶动刚度随地表液化土厚度的增加而降低。桩顶动阻尼在低频激振下，随着液化土厚度的增加而下降，而在高频激振下，当液化土厚度比例达到0.2 时，动阻尼随激振频率变化的速度加快。

（2）当激振频率小于4 Hz 时，流体密度对桩基的动刚度影响不明显，随着频率进一步增大，高桩桩顶动刚度随密度的增大而减小。流体密度对于桩基动阻尼的影响则更小，只有在10 Hz 以上的频率激振作用下，液化土密度对桩基动阻尼的影响才会有所展现。

（3）桩顶动刚度随竖向荷载增大而减小，相较于水平动刚度，竖向荷载对于摇摆动刚度影响更明显；与之相反的是，竖向荷载对于桩基的动阻尼影响并不明显，不影响能量在桩土系统中的耗散效率。因此在高桩设计中需合理选取竖向荷载值。