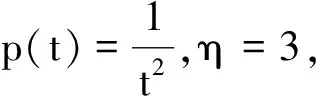一类带阻尼项的分数阶微分方程的振动性质

林文贤, 黄肖慧

(1.韩山师范学院 数学与统计学院,广东 潮州 521041; 2.江门市蓬江区教师发展中心,广东 江门 529000)

0 引言

分数阶微分方程是用于描述科学和工程领域的许多实际过程和现象的数学模型,如族群动态、神经网络、工业机器人、黏弹性、电路、最优控制、生物技术、经济学。近年来,分数阶微分方程理论取得了很大的进展[1-5]。振动现象普遍存在于自然界和工程技术等领域,如桥梁的振动、汽车发动机的振动、建筑物的振动、地震的振动、航空器的结构振动、化学反应过程中的复杂振动等,因而在分数阶微分方程的研究中,解的振动性理论受到广泛关注[6-12]。在振动性理论中,阻尼项起着重要作用。为此,本文将讨论如下带阻尼项的非线性分数阶微分方程

(1)

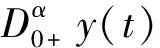
(H1)r(t)∈C1([t0,∞),(0,∞)),p(t),q(t)∈C([t0,∞),[0,∞));

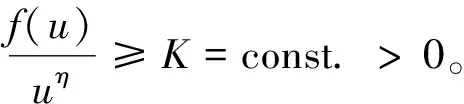
本文注意到文献[11]研究了在r=1,p∈C([t0,∞),(-∞,0))和η=1的情形下方程(1)解的振动性问题,文献[12] 研究了在η=1的情形下方程(1)解的振动性问题。

本文的目的是继续文献[11-12]的研究, 建立方程(1)的若干振动准则,推广和改进文献[11-12]的结果, 并给出实例加以阐述。

定义1[1]称

(2)

为函数y：(0,∞)→R的α阶Riemann-Liouville分数阶积分,如果(2)式的右端在(0,∞)上是逐点定义的,这里α>0为一常数,Γ是通常的Gamma函数。

定义2[1]称

(3)

为函数y：(0,∞)→R的α阶Riemann-Liouville分数阶导数,如果(3)式的右端在(0,∞)上是逐点定义的,这里α>0为一常数,n=[α]+1,[α]是α的整数部分。

引理2[13]假设y(t)是方程(1)的一个解,且

引理3[14]设λ>1,U≥0,V≥0,则有λUVλ-1-Uλ≤(λ-1)Vλ。

1 主要结果

定理1 若对某一个t0>0有

(4)

(5)

证明：设y(t)是方程(1)的一个非振动解。不妨设y(t)是方程(1)的一个最终正解,则存在t1≥t0,使得y(t)>0及G(t)>0,t≥t1。利用引理1,由方程(1)、条件(H1)和(H2), 可得

(6)

(7)

利用引理2,有

(8)

对式(8)从t2到t积分,可得

(9)

定义Riccati变换

(10)

则w(t)>0,t≥t1。利用引理1,由式(1)和(10),可得

(11)

取

由式(11)和引理3有

(12)

对式(12)从t1到t积分得

下面利用Philos型的积分平均技巧[15],得出方程(1)的新的振动定理。为此引进如下一类函数J。令

D={(t,s)|t≥s≥t0},D0={(t,s)|t>s≥t0}。

函数H(t,s)∈C(D,R)称为属于J类, 记作H∈J, 如果

(ⅰ)H(t,t)=0,t≥t0;H(t,s)>0,(t,s)∈D0;

(13)

证明：设y(t)是方程(1)的一个非振动解。不妨设y(t)是方程(1)的一个最终正解。如同定理1的证明,可以得到式(11),两边乘以H(t,s),并从t1到t-1积分得

(14)

由分部积分法,有

(15)

将(15)代入(14)得

(16)

取

由式(16)和引理3有

(17)

(18)

令t→∞,有

与条件(13)矛盾。定理2证毕。

注：文献[11]研究了方程(1)当r=1和η=1的情形下解的振动性问题, 文献[12] 研究了在η=1的情形下方程(1)解的振动性问题, 定理1和定理2推广和改进文献[11-12]的结果。

2 应用

例1 考虑分数阶微分方程

(19)

及

因此,定理1的条件全部满足,从而方程(19) 的所有解都振动。