基于RESYS程序的TOPAZ-Ⅱ反应堆系统模拟

吴宗芸,祁 琳,吴明宇,李杨柳,杨宏伟,刘天才

(中国原子能科学研究院 核工程设计研究所,北京 102413)

随着“天问一号”探测器成功到达火星以及“祝融号”火星车成功登录,我国的深空探测技术迈上了新的台阶,未来的航天事业迈向深空领域已成必然趋势。这也意味着未来的深空航天器需要运用与深空探测相适应的能源技术。空间核反应堆电源不依赖于太阳的光照以及其他的环境因素,能提供大功率的电能,是理想的用于深空探测的能源。美国和前苏联在20世纪50年代开始了空间反应堆电源的研究,而热离子热电转换可以是一种用于空间核电源的静态热电转换技术。早在20世纪60年代,前苏联开始建造用于给卫星提供能源的单节型和多节型热离子系统[1],其设计的TOPAZ反应堆系统是最为先进的热离子反应堆。TOPAZ-Ⅱ[2]是前苏联所设计的单节型热离子核反应堆系统。

美国对TOPAZ-Ⅱ反应堆进行了大量的实验测试研究。除了实验研究外,美苏两国均对TOPAZ-Ⅱ反应堆进行了相应的数值模拟研究。El-Genk开发了二维瞬态的单节型热离子燃料元件模拟程序[3]以及用于热离子反应堆稳态和瞬态模拟的TITAM程序[4]。El-Genk利用TITAM程序分析了TOPAZ-Ⅱ反应堆在启动过程中特性和稳态工况下的铯压、负载电阻等因素对反应堆系统的影响[5],并完成了其在轨启动时的事故工况分析[6]。TITAM程序使用集总参数的模型,所以无法对一些详细的参数进行分析。除此以外美苏两国还开发了ENSY[7]、TFETC[8]、CENTAR[9]等程序。国内也对TOPAZ-Ⅱ系统的数值模拟进行过相应的研究,TASTIN程序[10]是张文文等专门针对热离子空间堆开发的系统分析程序,相对于TITAM其使用更加细致的热工模型,可详细地计算堆芯的温度分布以及辐射散热器的温度分布等,但在公开的文献[10-11]中,该程序未对热离子热电转换系统进行建模;另外,Tang等[12]使用经过修改后的RELAP5程序对TOPAZ-Ⅱ反应堆进行了反应性引入事故(RIA)、失冷事故(LOCA)以及失流事故(LOFA)分析,初步验证了TOPAZ-Ⅱ反应堆在事故工况下的安全性。

通用的系统分析程序可方便地对反应堆进行建模,所以使用通用系统分析程序来建立空间核反应堆的模型是一种很好的研究思路。然而虽然经过改进后的针对轻水反应堆开发的RELAP5程序能够对TOPAZ-Ⅱ反应堆进行一定的分析,但RELAP5、TRACE这类程序没有对热离子热电转换系统、空间堆中广泛使用的热管辐射散热器等部件进行建模的能力,这限制了传统针对轻水反应堆开发的系统分析程序在空间核反应堆中的应用。因此,本文使用C++语言开发面向先进核动力系统的反应堆的通用系统分析程序RESYS,并在其基础上建立TOPAZ-Ⅱ反应堆的堆芯、热排放系统辐射散热器模型,热电子发射电流密度模型、电气系统模型,以对TOPAZ-Ⅱ的稳态和瞬态启动工况进行分析。

1 RESYS程序简介

RESYS程序采用和RELAP5程序类似的控制体建模的方式来对核反应堆系统进行建模:程序使用管型部件、接管、分支部件、热构件等通用部件来描述整个核反应堆系统。RESYS程序的输入设计参考了RELAP7[13]、SAM[14]等最近十年内开发的反应堆系统分析程序的输入设计,提高了用户的友好性。程序整体上使用面向对象的结构设计,并且在程序内部支持面向对象的建模,提高了程序的可维护性以及基本模型的可重用性。并且程序支持直接读取RELAP5的tpf格式[15]的物性文件,可直接利用之前针对RELAP5程序开发的物性库以及RELAP5-3D中已有的各种冷却剂工质物性包。在算法方面,程序采用Jacobi预处理的Newton-krylov子空间迭代法[16]以全隐式的方式来计算反应堆系统中的共轭传热问题,包含内置的矩阵求解器以及与科学计算可移植扩展工具包PETSc[17]的接口,相比于传统的系统分析程序使用算子分裂求解的方式,Newton-krylov子空间迭代法提高了求解与收敛的效率;程序中点堆动力学方程采用求解刚性常微分方程的Gear算法[18]求解。程序可在Windows系统和Linux系统中运行,具有良好的可移植性。图1示出RESYS程序的计算流程,主要的求解步骤分为辅助模型求解、流量压降求解和传热求解。

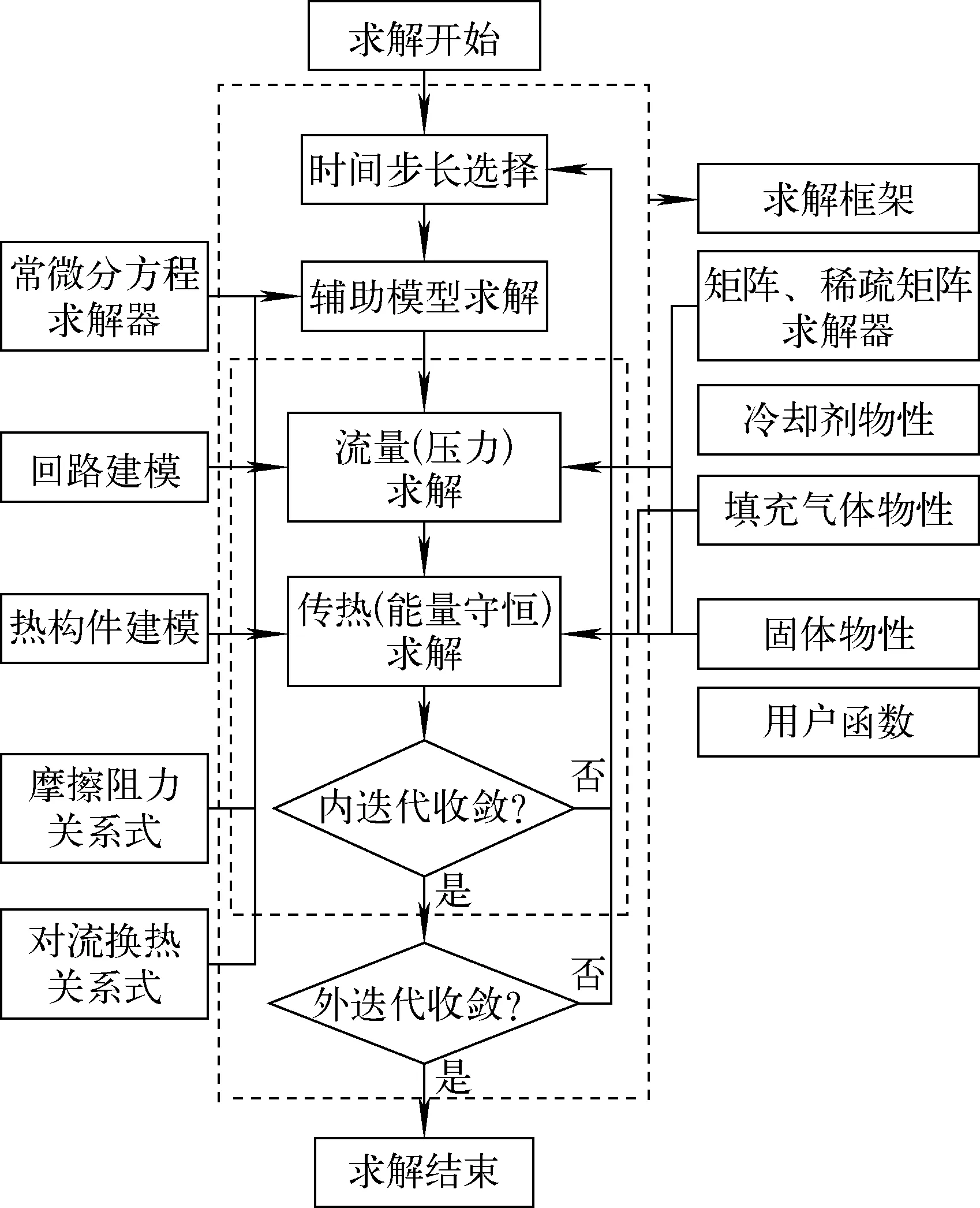
图1 RESYS程序计算流程图Fig.1 Calculation flow chart of RESYS code

2 TOPAZ-Ⅱ反应堆系统模型的建立

TOPAZ-Ⅱ反应堆系统是一个使用热离子静态热电转换方式的热离子空间反应堆。图2为在RESYS程序中建立的TOPAZ-Ⅱ反应堆的系统模型。冷却剂NaK合金从反应堆下腔室流入反应堆堆芯,然后通过热离子燃料元件(TFE)的冷却剂流道从反应堆堆芯中带走大部分热量,在这个过程中冷却剂的温度升高。然后冷却剂流入反应堆上腔室,之后从两个分支流入到管式辐射散热器的上集流环,再通过带铜翅片的辐射散热器将热量通过热辐射的方式排出到周围的环境中,与此同时冷却剂的温度下降。冷却剂从辐射散热器的下集流环中分两个分支流出,其中右端的分支与体积补偿器相连,体积补偿器的作用是稳定系统压力并且提供冷却剂由于膨胀和收缩引起的体积变化的空间。冷却剂NaK合金流经电磁泵后流回到反应堆下腔室,然后再流经堆芯带走堆芯热量。电磁泵提供冷却剂流动的驱动压头。在TOPAZ-Ⅱ反应堆中一个非常关键的部件是堆内单节型热离子燃料元件和TFE电气系统,其承载了热离子反应堆的热电转换功能。在TOPZA-Ⅱ反应堆正常运行工况下,约会产生4.5～5.5 kW的电功率以给负载供给电能[2]。

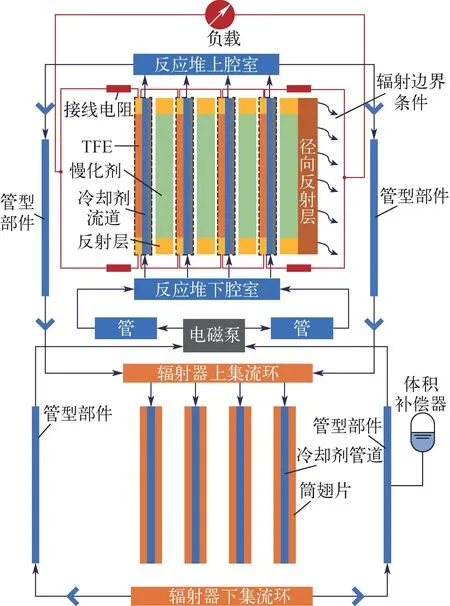
图2 在RESYS程序中建立的TOPAZ-Ⅱ反应堆系统模型示意图Fig.2 Schematic diagram of TOPAZ-Ⅱ reactor system model established in RESYS code

2.1 热离子燃料元件模型

在TOPAZ-Ⅱ反应堆中,最为核心的部件是堆内单节型全长热离子燃料元件。图3为TOPAZ-Ⅱ反应堆中心热离子燃料元件的结构示意图,其由内到外由高浓度二氧化铀燃料、发射极、接收极以及绝缘体、内不锈钢包壳、冷却剂流道、外不锈钢包壳以及慢化剂组成。在发射极与接收极的间隙中引入铯(Cs)蒸气,形成铯热离子能量转换器,以降低发射极的功函数、提高热离子能量转换器的输出功率以及延长使用寿命。在反应堆运行时,大部分的热量都由中心UO2陶瓷燃料发生裂变反应产生,热量以辐射、热传导等方式通过燃料与发射极间的气隙传入给发射极,表面镀有钨的钼铌合金发射极受热后发生热电子发射效应,部分电子克服表面势垒而逸出发射极。逸出发射极的电子穿越电极间隙到达接收极从而在接收极与发射极间产生电势。而传入到发射极的大部分热能以辐射传热和热传导的方式传递给接收极,最终大部分热量通过绝缘材料和不锈钢包壳后由NaK合金冷却剂带出,然后通过辐射散热器释放到环境中,而部分热能通过电极热电子发射的方式转换为电能。

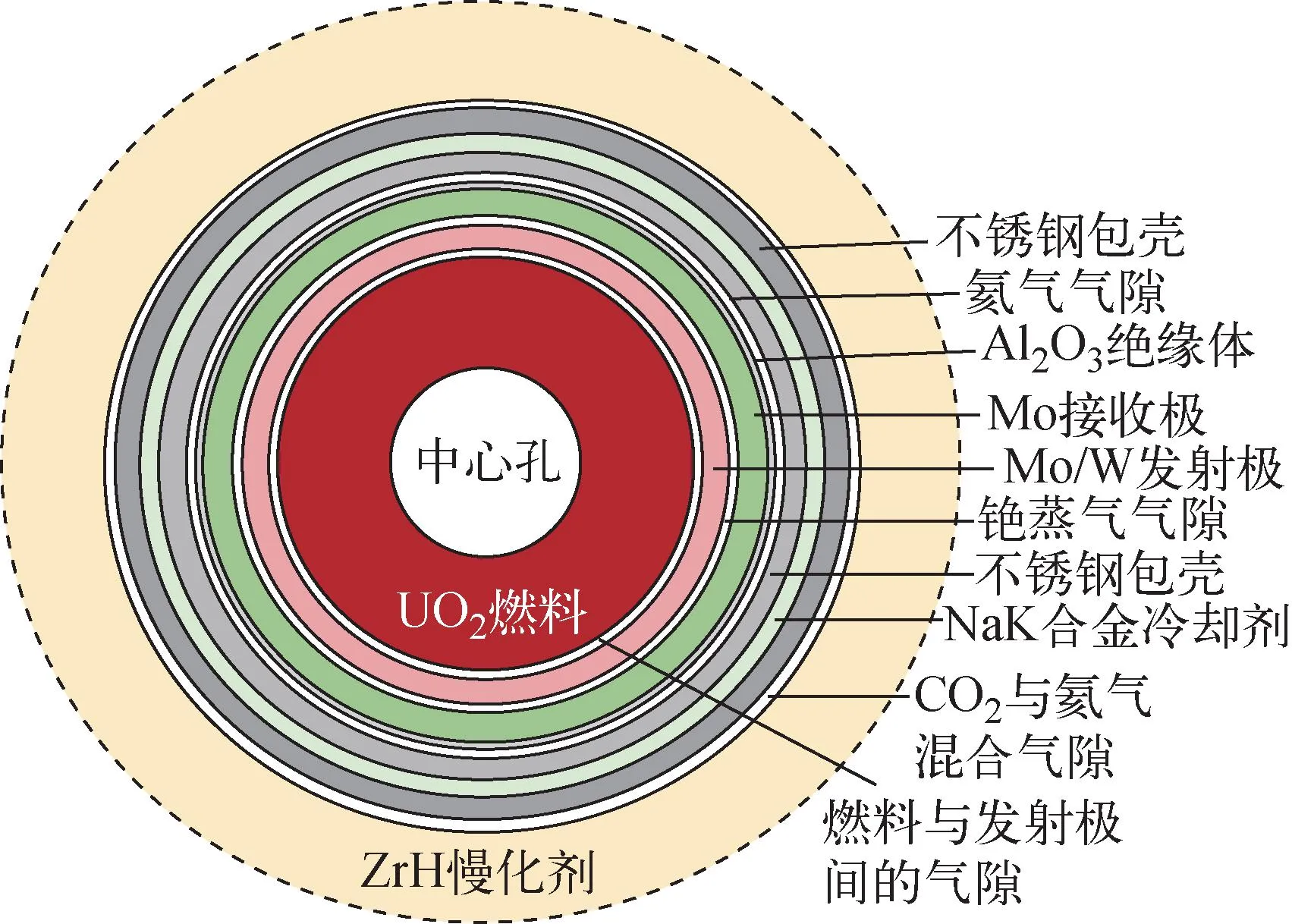
图3 热离子燃料元件结构示意图Fig.3 Structural diagram of thermionic fuel element

本文在RESYS程序中通过面向对象的建模方式建立了热离子燃料元件的模型,其中热离子燃料元件中的UO2燃料、发射极、接收极与绝缘材料、内不锈钢套管、外不锈钢套管均采用RESYS程序中的C++类cylindricalHeatStructure来实例化1个具体的柱状热构件模型来对其进行模拟,该类用于模拟柱状热构件的一维或二维热传导方程:

(1)

式中:ρs为固体材料的密度;Cs为固体材料的比热容;Ts为热构件的温度;k为热导率;Qv为单位体积内的热源。当只考虑一维径向方向上的热传导时,式(1)中等号右端第2项被省略,从而忽略轴向方向上的热传导。本文研究中,所有热构件的热传导计算均考虑了轴向方向上的热传导。

对于热离子燃料元件中燃料与发射极气隙、Al2O3绝缘体与内不锈钢套管、外不锈钢套管与慢化剂间的气隙的传热过程使用RESYS程序中的surface_coupling C++类来对其进行建模。RESYS中的surface_coupling类可描述热构件间隙的辐射换热、热传导、接触换热过程,由于这些效应导致的气隙总的热流密度qall为:

qall=qr+qk+qc

(2)

qr为由于热辐射效应带来的热流密度:

hr(T1-T2)

(3)

式中:ε1、ε2分别为内、外表面的发射率;A1、A2分别为内、外表面的面积;T1、T2分别为内、外表面的温度。

qk为由于间隙填充气体的热传导带来的热流密度:

(4)

式中:kg为间隙气体的热导率;d为间隙的宽度。本文中,由于不涉及到接触传热,因此不对接触传热的热流密度qc的计算公式进行介绍。

而对于发射极与接收极间的铯蒸气气隙,由于通过该间隙的能量方式不仅有辐射换热、热传导,还有由于发射热电子带来的电极间隙的能量转移:发射极发射热电子导走能量带来的发射极电子冷却效应以及接收极接收热电子导致的接受极电子加热效应。这样,发射极发射电子到接收极的同时,相当于也将部分能量通过电子发射的方式传递给接收极。由于单节型热离子燃料元件电极较长,流过电极的电流很大,在电极上会产生较高的焦耳热从而加热电极。在RESYS程序中,通过thermionic_surface_coupling C++类来描述发射极与接收极的能量传递过程,该类继承于描述气隙传热的surface_coupling类,因此也可模拟间隙的辐射换热、热传导、接触换热过程,但它还可模拟电极发射接收电子带来的电子冷却、电子加热,以及发射极、接收极上产生的焦耳热。

对于发射极,由于焦耳热与发射电子在电极上产生的总热量QE为:

(5)

对于接收极,由于焦耳热和接收电子在接收极上产生的总热量QC为:

(6)

其中:TE、TC分别为发射极和接收极的温度;IE、IC分别为发射极和接收极上的电流强度;RE、RC分别为发射极和接收极的电阻率;φE、φC分别为发射极和接收极的功函数。

发射极的功函数[5]为:

φE(eV)=-62.9+73.7(TE/TR)-

33.3(TE/TR)2+7.5(TE/TR)3-

0.82(TE/TR)4+0.035(TE/TR)5

(7)

其中,TR为铯发生器温度。

接收极的功函数[5]为:

φC(eV)=15.8-21(TC/TR)+

10(TC/TR)2-1.5(TC/TR)3

(8)

铯蒸气的热导率[19]为:

(9)

其中:d为电极间距,cm;pCs为铯蒸气压,torr(1 torr=133.3 Pa)。

接收极与发射极间的电流密度J受发射极与接收极功函数、电极间距、铯温铯压以及电极两端的输出电压影响,即J=J(TE,TC,pCs(TCs),d,Vout),因此决定电极间电流的因素非常复杂。在RESYS程序中,发射极与接收极间的J由Rasor电流密度模型[20]计算:

Vout=φE-φC-Vd+ΔV

(10)

关于Rasor模型的公式的详细参数以及说明参考文献[20],本文在此省略了大部分公式。图4示出使用Rasor模型计算得到的不同发射极温度以及不同输出电压Vout下的电流密度和实验[21]得到的结果的对比。可看出,Rasor电流密度模型计算得到的电流密度结果和实验值[21]相比,整体上符合得较好,没有量级上的误差,证明了本文开发的Rasor电流密度模型计算模块的准确性。图5示出在不同的发射极温度下,输出电流密度随输出电压的变化。可看出,电极间的电流密度J随着输出电压的增大而逐渐减小,并且当输出电压小于0.5 V时,电极间电流随发射极温度升高而降低,这是由于发射极温度升高增大了发射极的功函数,从而降低了发射极的发射的电子流密度。

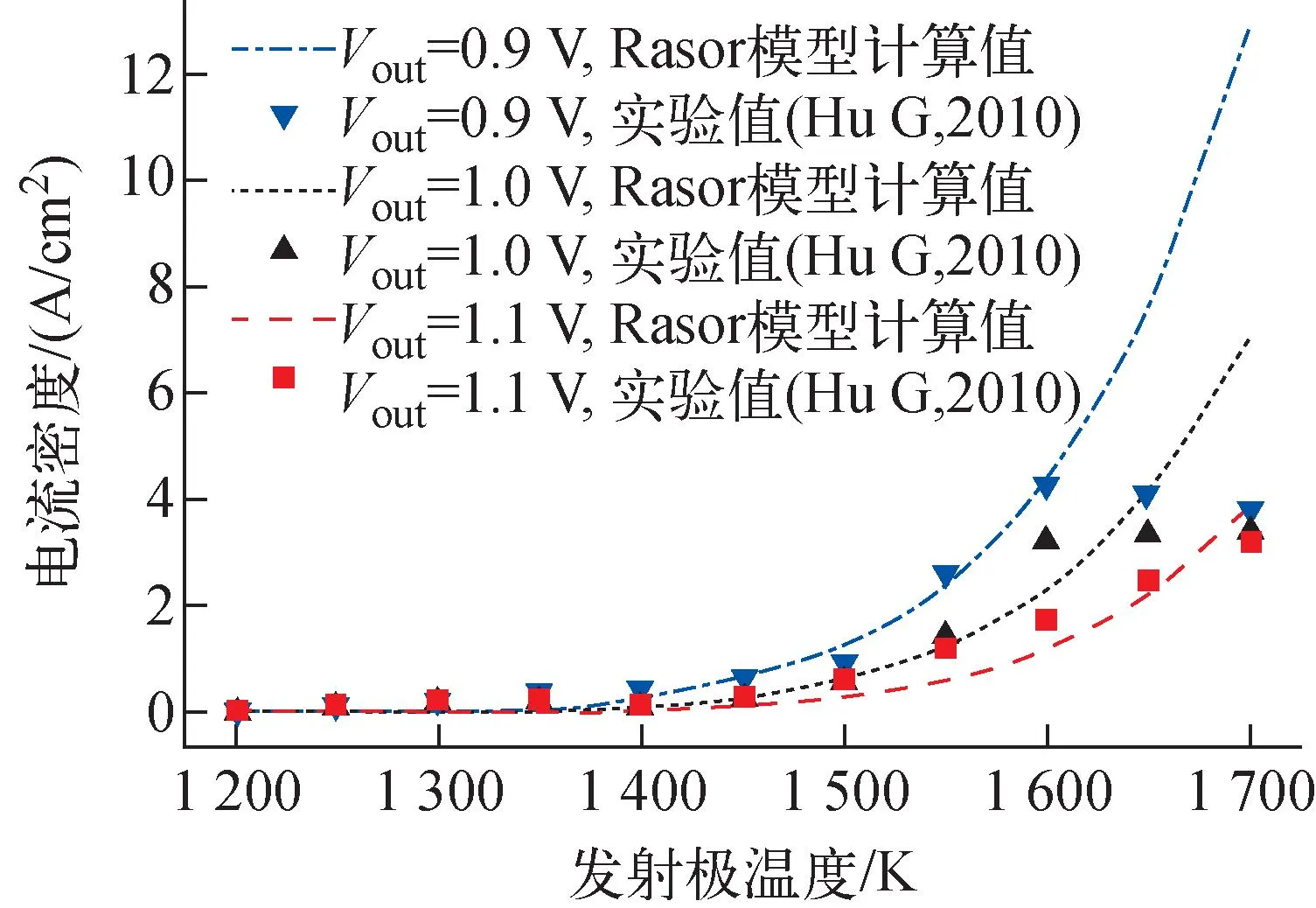
图4 不同发射极温度下与不同输出电压下电流密度计算值与实验值的对比Fig.4 Comparison between calculated value of current density and experimental value under different emitter temperatures and output voltages

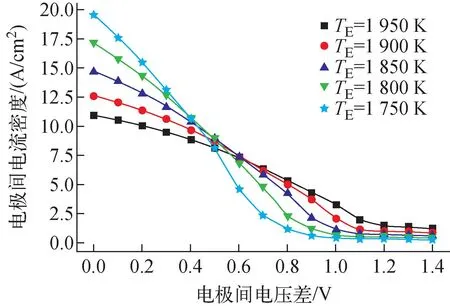
图5 不同发射极温度下电流密度模型的伏安特性曲线Fig.5 Volt ampere characteristic curves of current density model at different emitter temperature

NaK合金冷却剂流过热离子燃料元件的冷却剂流道,与不锈钢内、外套管发生对流换热,带走从堆芯产生的大部分能量。在RESYS程序中,使用flowComponent C++类对冷却剂的一维流动换热进行建模,其描述一维单相流动的质量、动量、能量守恒方程为:

(11)

(12)

(13)

2.2 TFE电气系统模型

TOPAZ-Ⅱ电气系统由热离子燃料元件的发射极、接收极,接线电阻以及负载组成。TOPAZ-Ⅱ反应堆使用双线串联的方式将热离子燃料元件的发射极和接收极相接。RESYS程序中建立的TOPAZ-Ⅱ反应堆TFE电气系统模型如图6所示。由于TOPAZ-Ⅱ反应堆中热离子燃料元件从内向外共分为4圈,考虑到热离子燃料元件的对称布置,图6中每对发射极和接收极代表TOPAZ-Ⅱ堆芯中同一圈的热离子燃料的电极,因此图6中包含4对电极。热电子从发射极发射到接收极的同时,电流通过电极间隙由接收极流向发射极,发射极的电流从电极两端的接线柱通过导线流入另外一个热离子燃料元件的接收极,然后再通过热电子发射效应穿过间隙流向发射极。由于使用双端串联的方式连接不同燃料元件的电极,因此穿过每个电极间隙的总的电流之和总是相等的。为了简化方程的求解,本文的研究中使用了更加严格的假定:流入接收极上端(下端)的电流等于从发射极上端(下端)流出的电流。如图6所示,流入流出电极下端的电流使用I1表示,流入流出电极上端的电流使用I2表示。那么,根据欧姆定律可得到整个负载系统的方程:

图6 TOPAZ-Ⅱ反应堆TFE电气系统模型示意图Fig.6 Schematic diagram of TFE electrical system model of TOPAZ-Ⅱ reactor

(I1+I2)RL=-(R2+R4)I1+N1ΔU1,1+

N2ΔU2,1+N3ΔU3,1+N4ΔU4,1

(14)

(I1+I2)RL=-(R1+R3)I2+N1ΔU1,2+

N2ΔU2,2+N3ΔU3,2+N4ΔU4,2

(15)

式中:N1=1代表中心热离子燃料元件的数目,N2=6、N3=12分别代表第1圈、第2圈热离子燃料元件的数目;N4=15,虽然第3圈有18根热离子燃料元件,但其中有3根热离子燃料元件单独给电磁泵供给电源[22],因此不被计入到负载系统里面。对于每对发射极和接收极,由于发射极和接收极材料存在着电阻,因此电流流过发射极和接收极时,会导致电极上电势的非均匀分布。如图6所示,将接收极和发射极的活性区离散为多个轴向分段以求解每个分段上的电势φE,i、φC,i以及穿过电极的电流密度Ji,根据基尔霍夫定律可得到如下的关系式:

(16)

(17)

将式(15)与(16)相减,得到最终求解的方程:

(18)

式中:Δφi=φE,i-φC,i,为发射极与接收极之间的电势差;Ji(Δφi)为电极间的电流是电极间电势差Δφi的函数,其使用前面所给出的Rasor电流密度模型确定,取Vout=Δφi。通过迭代求解上面的方程可得到每圈热离子燃料元件的电极间电流密度分布、电势分布以及提供给负载的总电流和总功率,进而计算得到TOPAZ-Ⅱ反应堆的热电转换效率。在迭代求解时,首先假定双端串联的电流I1、I2,然后再根据方程求解电极两端输出电压ΔUi,1和ΔUi,2,之后再根据负载的方程确定I1、I2,这样循环迭代直到收敛为止。

2.3 反应堆本体模型

由于TOPAZ-Ⅱ反应堆堆本体采用固体ZrH慢化剂和反射层作为主体结构,同时堆本体的外表面与空间存在着热辐射,因此在计算时需计算堆本体的热传导并考虑外侧的热辐射边界条件,以考虑堆本体的辐射散热。在RESYS程序中,利用cylindricalHeatStructure模型来对堆本体进行建模,将其等效为1个圆柱状的热构件,并且最外侧设置为辐射换热边界条件。对堆本体进行二维控制体划分,如图7所示。对于ZrH慢化剂,将其沿着径向划分4层控制体,每层对应1圈的热离子燃料元件,并将径向反射层以及控制转股进行相应的控制划分。对于慢化剂控制体,其截面积为总面积减去TFE所占的面积,相邻的控制体的径向距离为相邻两圈控制台的中心的间距。在轴向上,节点的划分的控制体长度与热离子燃料元件的相同。在计算时,由于RESYS程序提供全系统耦合的计算能力,其与热离子燃料元件的传热被隐式耦合同时求解。

2.4 热排放系统模型

TOPAZ-Ⅱ热排放系统主要包括电磁泵、体积补偿器、辐射器等部件。体积补偿器起到稳定系统压力的作用,因此在使用RESYS程序中的时间相关控制体(time dependent volume)对其进行建模,其在模型中起压力参考点的作用。电磁泵为回路冷却剂流动提供驱动压头,在RESYS程序中使用idealPump模型模拟电磁泵以给冷却剂回路提供冷却剂流量。反应堆堆芯产生的热能除了在热离子电极间由于发射热电子损耗外,其余均由NaK合金带出堆芯并在辐射散热器排放到外界环境中。此处主要介绍在RESYS程序中建立的TOPAZ-Ⅱ的辐射散热器模型。

TOPAZ-Ⅱ反应堆使用回路式的辐射散热器,该辐射散热器为圆台形外观,主要包括上集流环、下集流环、78根冷却剂长管以及长管外包覆的铜翅片[23]。冷却剂从上集流环流入冷却剂长管后,流经长度约为1.8 m的冷却剂长管与管壁发生对流换热,热量最终通过管壁与外面包覆的铜翅片排放到外界的环境中。本文研究中,使用RESYS程序中的pipeWithHeatstructrue部件对TOPAZ-Ⅱ的辐射散热器散热部分进行建模。对于辐射散热器,考虑到其对称性,使用4个通道模拟整个辐射器的特性,每个模拟上、下集流环入口和出口间的1/4辐射散热器的散热。pipeWithHeatstructrue部件描述热构件与一维流动部件耦合的换热问题。其中一维流动部件用来模拟冷却剂在辐射器冷却剂长管中的对流换热,笛卡尔几何的热构件模型用来模拟铜翅片的传热。由于铜翅片的宽度和长度远大于其厚度,因此使用二维非稳态的热传导方程来考虑在铜翅片上传热是合理的,铜翅片的上表面与下表面的辐射散热通过热传导方程的热源项来考虑。在实际计算中为了增加数值稳定性,需要将热传导方程中的辐射散热源项进行线性化处理:

(19)

2.5 反应堆上腔室、下腔室模型

本文研究中,TOPAZ-Ⅱ反应堆的上腔室与下腔室的模型使用RESYS程序中的分支控制体部件(VolumeBranch)进行建模。Volume-Branch部件是一个拥有单个控制体的零维部件,其表示多个一维管型流动部件的交汇,用于多个一维管型部件的连接。该部件保证连接的多个一维流动部件之间的能量守恒与质量守恒,并且考虑了控制体的惯性效应(对应于质量守恒与能量守恒方程的非稳态项)。描述分支控制体的能量守恒与质量守恒方程为:

(20)

(21)

2.6 点堆动力学与反应性反馈模型

由于TOPAZ-Ⅱ反应堆堆芯的尺寸非常小,因此轴向与径向上的中子通量分布耦合得非常紧密,所以采用6组缓发中子点堆动力学足以模拟启动过程中反应堆的裂变功率随时间的变化,在RESYS程序中带有很强刚性的点堆方程采用Gear算法来求解。TOPAZ-Ⅱ反应堆的反应性反馈模型中考虑了燃料的多普勒反应性反馈、电极的反应性反馈、慢化剂与反射层的反应性反馈以及控制转鼓的反应性引入。

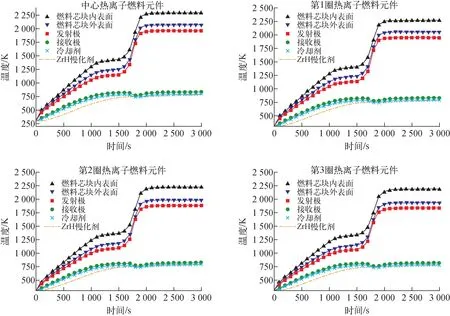
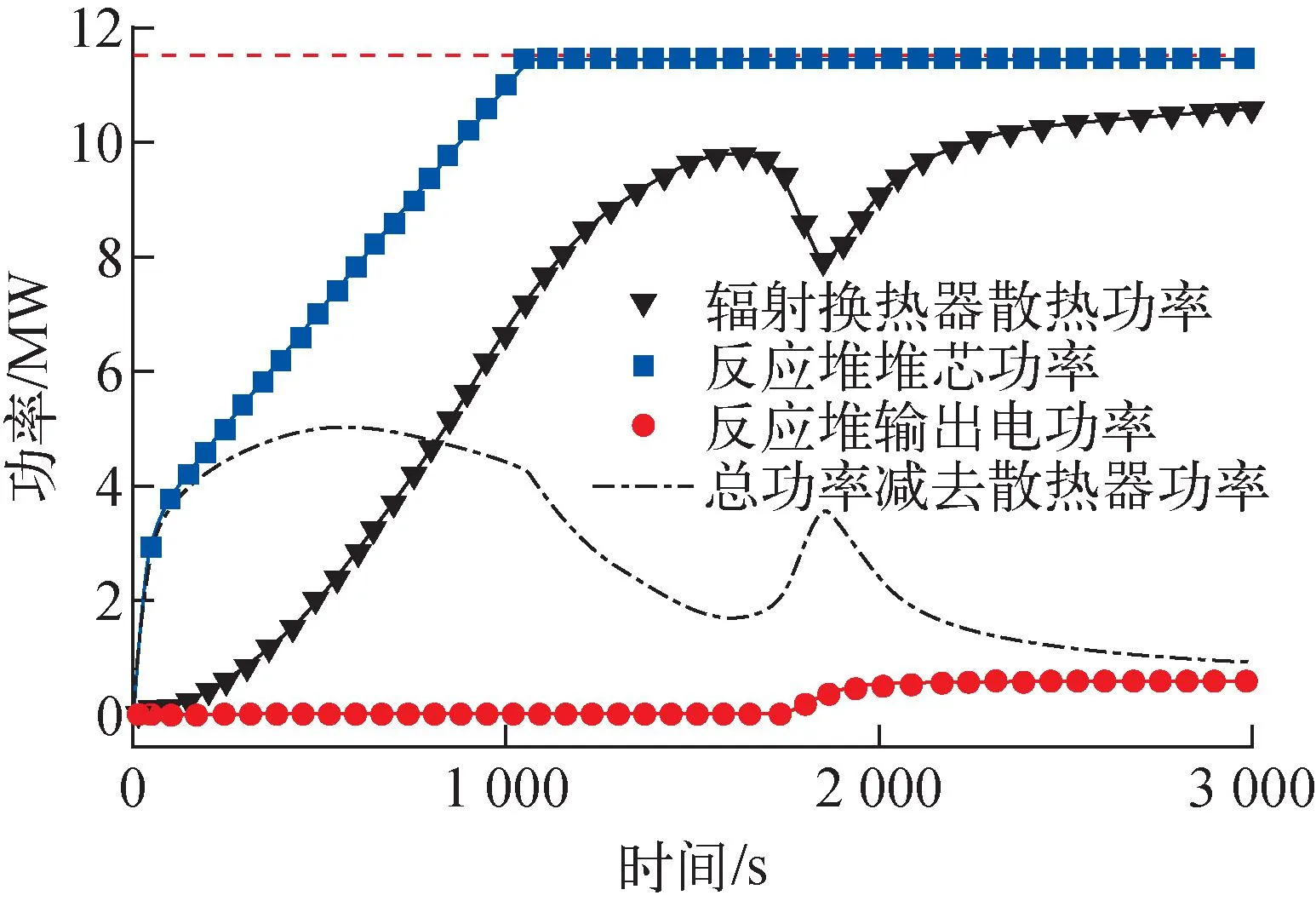
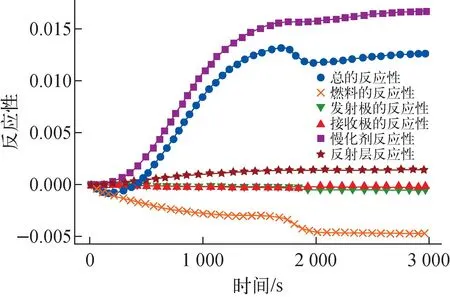
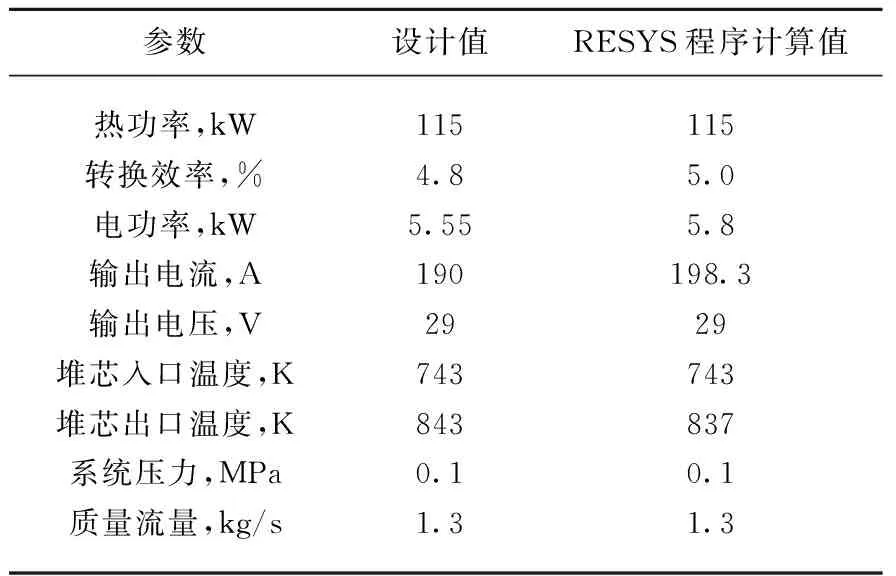
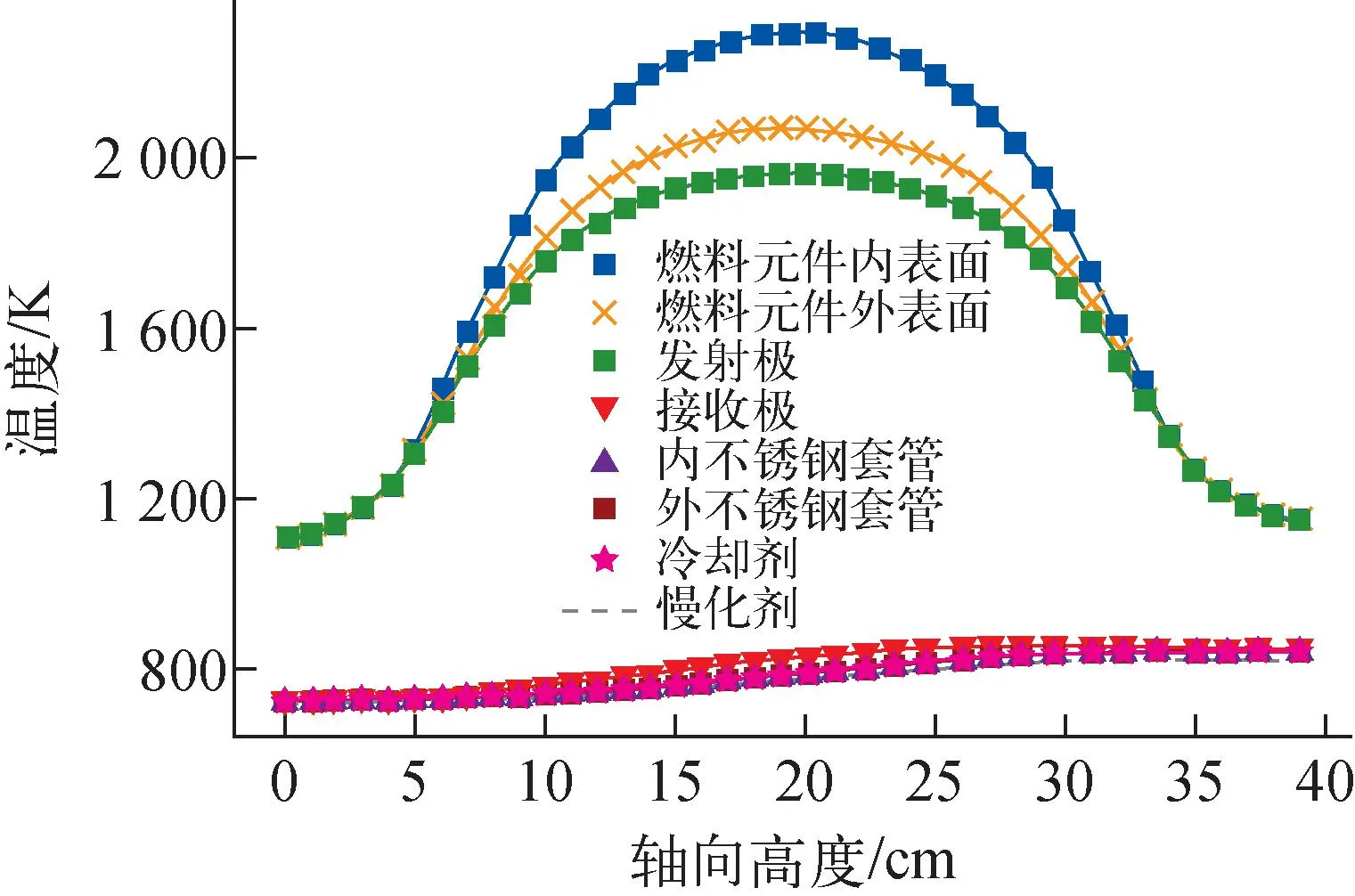
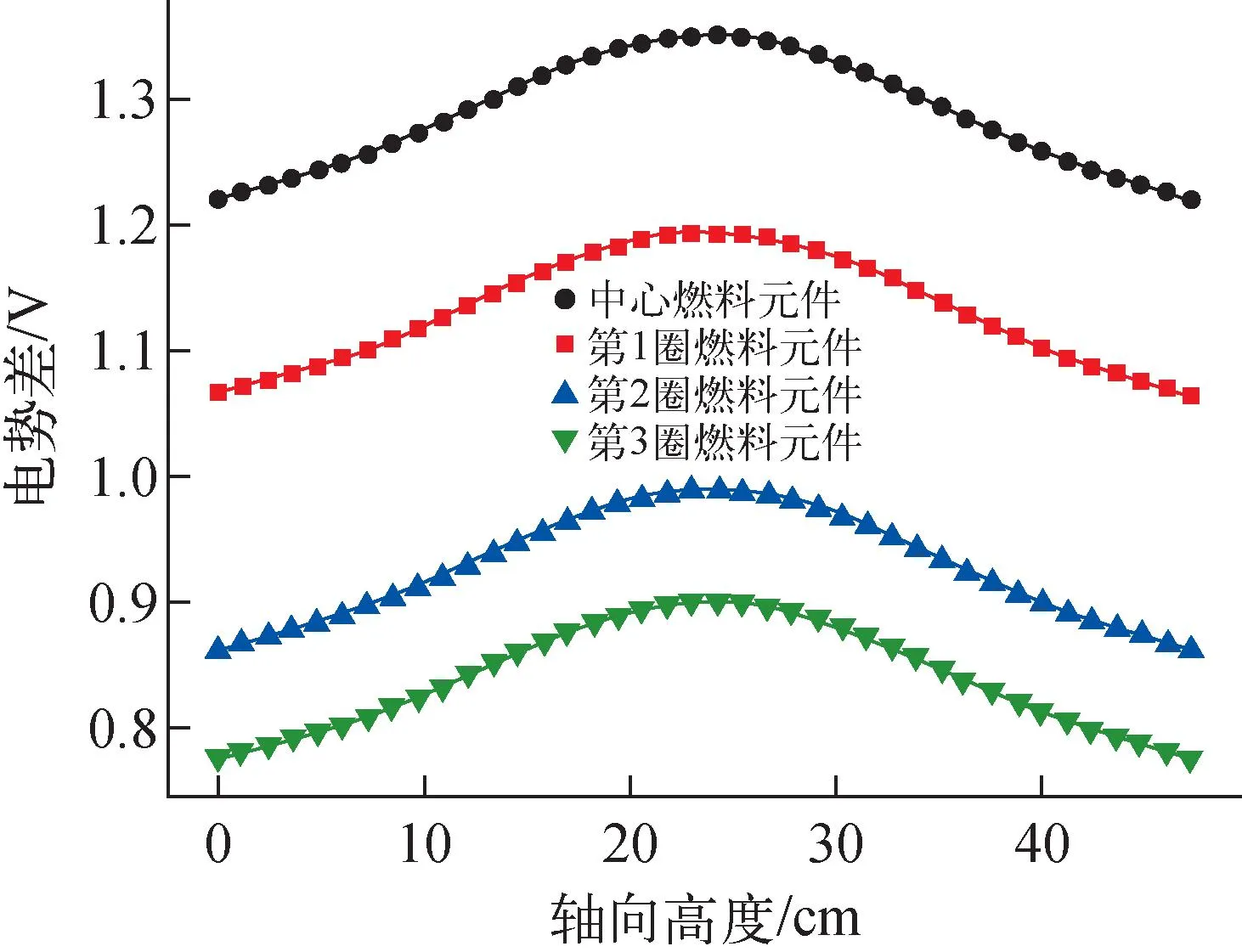
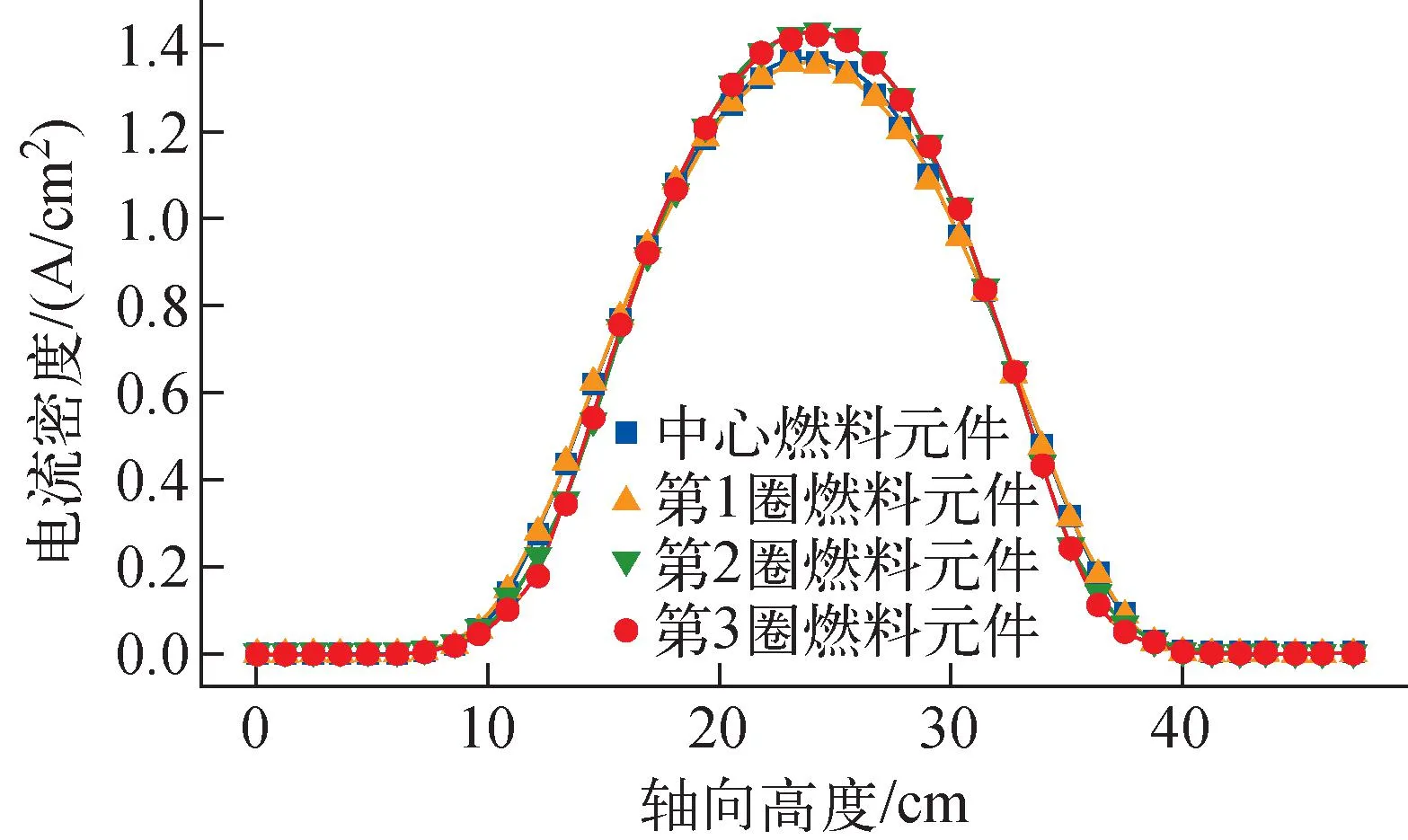
ZrH慢化剂引入反应性反馈(300 K

Δρm=(Tm-T0)[-8.22×

10-14(Tm-T0)4+1.6×10-10(Tm-T0)3-

1.11×10-7(Tm-T0)2+2.92×

10-5(Tm-T0)+1.76×10-3]

(22)

反射层引入反应性反馈(300 K

Δρref=0.38[1-(T0/Tref)0.5]

(23)

UO2燃料引入反应性反馈[5]:

(24)

电极引入反应性反馈(300 K

Δρel=8.52×10-2-4.26×10-2×

[(TE/T0)0.5+(TC/T0)0.5]

(25)

式(21)～(24)中,T0=300 K。

控制转鼓引入的反应性[5]为:

Δρel=-4.0-2.5×10-3θ+

3.72×10-4θ2+2.21×10-6θ3-

3.57×10-8θ4+9.41×10-11θ5

(26)

其中,θ为控制转鼓转动的角度,(°)。

总的反应性Δρ为各部分引入的反应性之和:

Δρ=Δρel+Δρf+Δρref+Δρm

(27)

3 模拟计算结果与分析

3.1 TOPAZ-Ⅱ反应堆启动模拟

TOPAZ-Ⅱ从冷态启动开始前,所有的控制鼓与安全鼓的转角都为0°,控制鼓和安全鼓的位置都朝向内侧,如图8所示,B4C反射体都朝向最外侧,这时反应堆处于次临界状态,keff=0.952。启动时,首先将3个安全鼓向外转动180°。之后以最大的转动速度将控制鼓向外转动154°,在反应堆功率升至5 kW以后,将控制鼓向内转至145°的位置。然后调节控制鼓的转动与朝向以600 W/s的速度升高功率到35 kW,之后以80 W/s的速度升高功率到115 kW。在这之后,调节控制转鼓转动以维持临界状态保持功率不变。在启动前,电极间充有气压为4 torr氦气进行保护,在1 500 s后,铯蒸气供应系统缓慢注入铯蒸气以代替氦气,TFE开始启动。在达到稳定状态后,电极间的铯蒸气的气压为2 torr。

图8 启动过程中各圈热离子燃料元件轴向中心平面温度随时间的变化Fig.8 Variation of temperature of thermionic fuel element with time during startup on axial center plane

在启动开始时,整个反应堆系统,包括反应堆堆芯、一回路冷却剂、辐射散热器的温度均为300 K。启动开始后,蓄电池立刻开始给电磁泵供电,电磁泵驱动冷却剂流过堆芯。图8为启动过程中热离子燃料元件轴向中心平面上各部分的温度变化。在启动初期,由于反应堆堆芯功率迅速上升,热离子燃料元件的燃料芯块与发射极的温度也迅速上升,随后反应堆堆芯功率上升速度减缓,燃料与发射极的温度上升速度也相应减慢。在启动后约1 070 s后,反应堆堆芯的功率达到稳定的115 kW水平,这时各圈的TFE的温度也逐渐趋于稳定,这时发射极的温度约为1 050 K。在启动1 500 s后,TFE开始启动,电极间的高热导率的氦气逐渐被低热导率的铯蒸气取代。因此电极间的温度差开始快速升高,TFE的燃料芯块与发射极的温度开始迅速升高,与之相反,接收极、冷却剂的温度在短暂的下降后又升高回原来的温度。而对于ZrH慢化剂,由于其与TFE间存在着充有二氧化碳的气隙,在启动过程中其温度上升的速度相比于其他部分的温度上升速度来说要慢得多。

图9为TOPAZ-Ⅱ反应堆在启动过程中的热平衡动态图。从图9可看出,由于TFE的启动,将电极间隙高热导率的氦气替换为低热导率的铯蒸气,导致燃料和发射极的温度升高并且部分裂变产生的热能存储在燃料中,使得冷却剂温度暂时降低并且辐射散热器的功率出现一个短暂下降后又上升的趋势。并且随着发射极的温度逐渐升高,电极间的铯压逐渐增大,反应堆的TFE电气系统在1 500 s启动后逐渐开始输出电功率。图9中,总功率减去散热器功率与反应堆输出电功率之间的差值代表着由反应堆本体辐射到外界环境中以及存储在反应堆系统中的能量。

图9 TOPAZ-Ⅱ反应堆启动瞬态过程中的热平衡Fig.9 Thermal energy balance in TOPAZ-Ⅱ reactor startup transient

图10为TOPAZ-Ⅱ反应堆在启动过程中的反应性随时间的变化。从图10可看出,TOPAZ-Ⅱ反应堆的反射层反应性和慢化剂反应性反馈均为正值,而ZrH慢化剂在系统中由于二氧化碳气隙的原因存在很强的热惯性,这增加了系统的控制难度。在启动的初期,由于二氧化铀燃料温度很快升高,使得在启动初期系统总的反应性反馈是负值,随后由于慢化剂与反射层的温度缓慢升高导致正的反应性反馈。在TFE启动后,由于燃料的温度升高,导致燃料的负反应性进一步加深,从而总的反应性反馈降低。由于TOPAZ-Ⅱ反应堆在整体上具有正的反应性反馈系数,因此不能依靠自身的负反馈维持自稳定性,这提高了反应堆控制系统的设计要求。

图10 TOPAZ-Ⅱ反应堆瞬态启动过程中的反应性反馈随时间的变化Fig.10 Variation of reactivity feedback coefficient with time during TOPAZ-Ⅱ reactor startup transient

3.2 TOPAZ-Ⅱ稳态系统工况分析

在反应堆启动阶段结束后,反应堆达到稳定的状态。图11为中心热离子燃料元件各部分在稳态时沿着轴向的温度分布。由于裂变功率在轴向上大致呈现为一个截断的余弦分布,导致燃料元件中心的温度远高于两端的温度分布,并且冷却剂在轴向的温升也呈现中间快两端减缓趋势。尽管两端的轴向反射层不发热,但由于热离子燃料元件采用二维的导热计算模型,发射极会向两端导热使得即使在轴向反射层区域发射极和接收极间也存在着相当的温差。在稳态时,中心热离子燃料元件内表面的最高温度为2 291 K,外表面的最高温度为2 066.55 K,发射极的最高温度为1 961 K,电极间的最大温差接近1 200 K,冷却剂入口的温度为743 K,堆芯的出口的温度为837 K。表1列出了RESYS程序计算得到的稳态工况与TOPAZ-Ⅱ设计值的对比。

表1 RESYS程序计算得到的稳态工况参数与设计值的对比Table 1 Comparison between designed value and calculated value of steady state condition by RESYS code

图11 稳态时中心热离子燃料元件温度在轴向高度上的分布Fig.11 Temperature distribution of thermionic fuel element in axial direction under steady state

图12为稳态时各圈热离子燃料元件电极间隙间电势差在轴向高度上的分布。从图12可看出,由于电极材料间存在电阻的原因,电流由电极中间流向两端的过程中存在着电压降,所以计算得到的热离子燃料元件的电势差在轴向上呈现中间高两端低。并且,由于各圈的热离子燃料元件在径向上的非均匀功率分布:越靠外圈的燃料元件其核功率越低,所以计算得到的电极电势差越靠外圈越低。中心热离子燃料元件电极间的电势差最高,其输出的电压也最高;而最外圈的电势差最低,输出的电压也低。

图12 稳态时各圈热离子燃料元件电极间隙间电势差在轴向高度上的分布Fig.12 Distribution of potential difference between electrode gaps of thermionic fuel elements in axial direction under steady state

图13为各圈TFE电极间的热电子发射电流密度在轴向上的分布。由于电极采用双端串联的方式连接,因此对于各圈的TFE,其热电子发射电子流密度值之和必然与串联的其他TFE相等,但由于各圈热离子燃料元件功率水平不同(堆芯的功率分布使用MCNP计算给出),其输出的电压有很大的差别。RESYS程序计算得到TOPAZ-Ⅱ反应堆在稳态时输出的总的电功率为5.8 kW,输出电压为29 V,输出电流为198.3 A;而由TITAM程序计算得到的TOPAZ-Ⅱ的输出功率为5.55 kW,输出电流为190 A[5]。RESYS程序计算得到的电功率与TITAM程序相比偏差在5%以内,因此可认为RESYS程序能较为准确计算出TOPAZ反应堆的输出电功率以及热电转换效率,由RESYS程序最终计算得到TOPAZ-Ⅱ反应堆的热电转换效率为5.04%。

图13 稳态时各圈热离子燃料元件电极间隙电流密度在轴向高度上的分布Fig.13 Distribution of current density in electrode gap of thermionic fuel element at axial direction under steady state

4 结论

本文基于面向先进反应堆的系统分析程序RESYS,使用面向对象的建模方式建立了TOPAZ-Ⅱ反应堆系统、热排放系统热工模型,并耦合了热离子静态热电转换电气系统模型、Rasor热离子发射电流密度模型,对TOPAZ-Ⅱ反应堆启动过程和稳态工况进行了分析。本文验证结果既验证了本文所开发的TOPAZ-Ⅱ反应堆的模型的合理性,也初步验证了所开发的RESYS程序的准确性与正确性。对于TOPAZ-Ⅱ反应堆启动过程与稳态工况,可得到如下结论。

1) RESYS程序计算得到的稳态电功率输出与TITAM程序计算得到的结果相对偏差在5%以内,与之符合良好。计算得到总的电功率为5.8 kW,输出电压为29 V,反应堆热电效率为5.04%。

2) 在启动过程中,慢化剂和反射层的反应性反馈为正,其在所有的反馈效应中占主导。TOPAZ-Ⅱ反应堆堆芯总的反应性反馈为正,不具有自稳定的负反馈效应,这增大了反应堆的控制难度。

3) 在TFE的启动过程中,由于电极间隙的气体热导率变化导致燃料芯块和发射极温度迅速升高,部分裂变产生的热能存储在燃料芯块中,使得冷却剂温度出现短暂下降且辐射散热器的功率也出现短暂下降。

本文工作可为后续针对TOPAZ-Ⅱ反应堆的控制策略研究以及事故分析提供很好的基础。本文使用的RESYS程序可为更多类型的反应堆的系统建模与仿真提供支撑。