循环荷载下花岗岩动力响应及本构模型

丁小彬, 赵君行, 董耀俊

(1.华南理工大学 土木与交通学院,广东 广州 510640;2.华南理工大学 华南岩土工程研究院,广东 广州 510640)

近年来,岩石动力响应的研究逐渐成为热点,许多学者通过不同的方法探究岩石动力响应的变化。何明明等[1]利用多功能材料试验机研究应力幅值、应力水平和含水率对砂岩、砾岩和砂砾岩动剪切模量和阻尼参数的影响。赵洪宝等[2]采用分离式霍普金森压杆对煤-岩和岩-煤两种复合岩体进行冲击试验。岩石动力响应受到许多因素的影响。梁书锋等[3]针对5个温度变量探究温度作用下的硅质砂岩试件力学性能,发现单轴抗压强度随岩石经历温度的升高而降低。刘恩龙等[4]发现岩石的残余轴向应变和体变随围压的增加而增加。聂明等[5]发现大理岩动弹性模量随循环周次增加而增大,随围压增大而减小;阻尼比和阻尼系数随循环周次增加而减小,随围压增大而增大。李明耀等[6]通过运用X射线、纳米压痕试验等方法研究花岗岩的细观力学特性及其结构特征对宏观力学性质的影响,发现花岗岩的宏观弹性模量随围压的增加呈增大趋势并趋于稳定。马林建等[7]利用微机伺服岩石三轴试验机在0.025～0.100 Hz下进行盐岩试样的循环荷载试验,发现加载频率越高,盐岩轴向应变-时间曲线滞回环面积越小,盐岩吸收能量比例减小,劣化速度随之降低。刘建锋等[8]对大理岩进行岩性试验,发现当应力幅值未达到岩石屈服应力时,动弹性模量随振动频率的变化不明显,而当应力幅值达到岩石屈服应力时,动弹性模量随着动应力幅的增大逐渐减小。何明明等[9]对砂岩、砾岩和砂砾岩进行了分级循环荷载试验,发现应力幅值增大时岩石内部矿物颗粒间胶结能力减弱,动弹性模量减小。朱明礼等[10]对花岗岩进行单轴压缩试验和循环加卸载试验,认为在低应力水平时循环应力对花岗岩的力学性质有循环强化效应,花岗岩的阻尼比和动弹性模量都是随循环周数的增加而减少。

目前,对于花岗岩动力响应的研究学者已经得到丰富的成果,但仍有一些不足之处：以往的研究往往仅能控制单一变量,较少能同时结合不同围压、动载频率、动应力幅,以及循环周次分析岩石动力响应,难以适用于实际工程中复杂的岩石应力状态;在实际工程中的低频地震作用以及交通荷载的频率分布范围在5～100 Hz之间[11],在之前的试验中频率选择大多为0.025～3 Hz[12],由于岩石动力响应存在频率依赖性,补充频率3 Hz以上的试验对于岩石动力响应的研究具有很大的工程意义。

因此,本文通过考虑岩石的弹塑性变形、滞后效应等情况计算出动弹性模量、动阻尼比,针对不同围压、动载频率、动应力幅以及循环周次对花岗岩动弹性模量以及动阻尼比变化规律进行探究,并对试验所得数据进行拟合。所得结论对前面学者进行的试验进行一个很好的补充,也为后续的岩石动力特性的反演分析研究提供系统、全面的理论支撑。

1 试验方案设计

本次试验使用真三轴试验机,控制加载频率≤20 Hz,最大围压为30 MPa,最大动应力幅为岩石最大抗压强度的35%左右。综合考虑试验仪器所能提供的最大压力、试件破坏所达到的应力幅值以及仪器在高频下捕捉数据的准确性,将动力应力幅分为6级。试验循环加载和卸载试验的方案如图1所示。加载过程分为两个阶段：第1阶段是线性静力加载,保持恒定的载荷率,达到预先设定的约束压力;第2阶段是动态循环加载,在约束压力达到预设值后循环正弦波加载,直到试样被破坏(图2)。试验所用花岗岩取自山东省日照市,采用水磨机对岩石进行切割,然后对岩石进行打磨、抛光,使其尺寸为100 mm×100 mm×100 mm。试验试件编号由加载条件确定,例如试件编号“Y1-5”表示动荷载频率为1 Hz,围压为5 MPa。采用控制变量法进行试验加载,试验组合如表1所示。

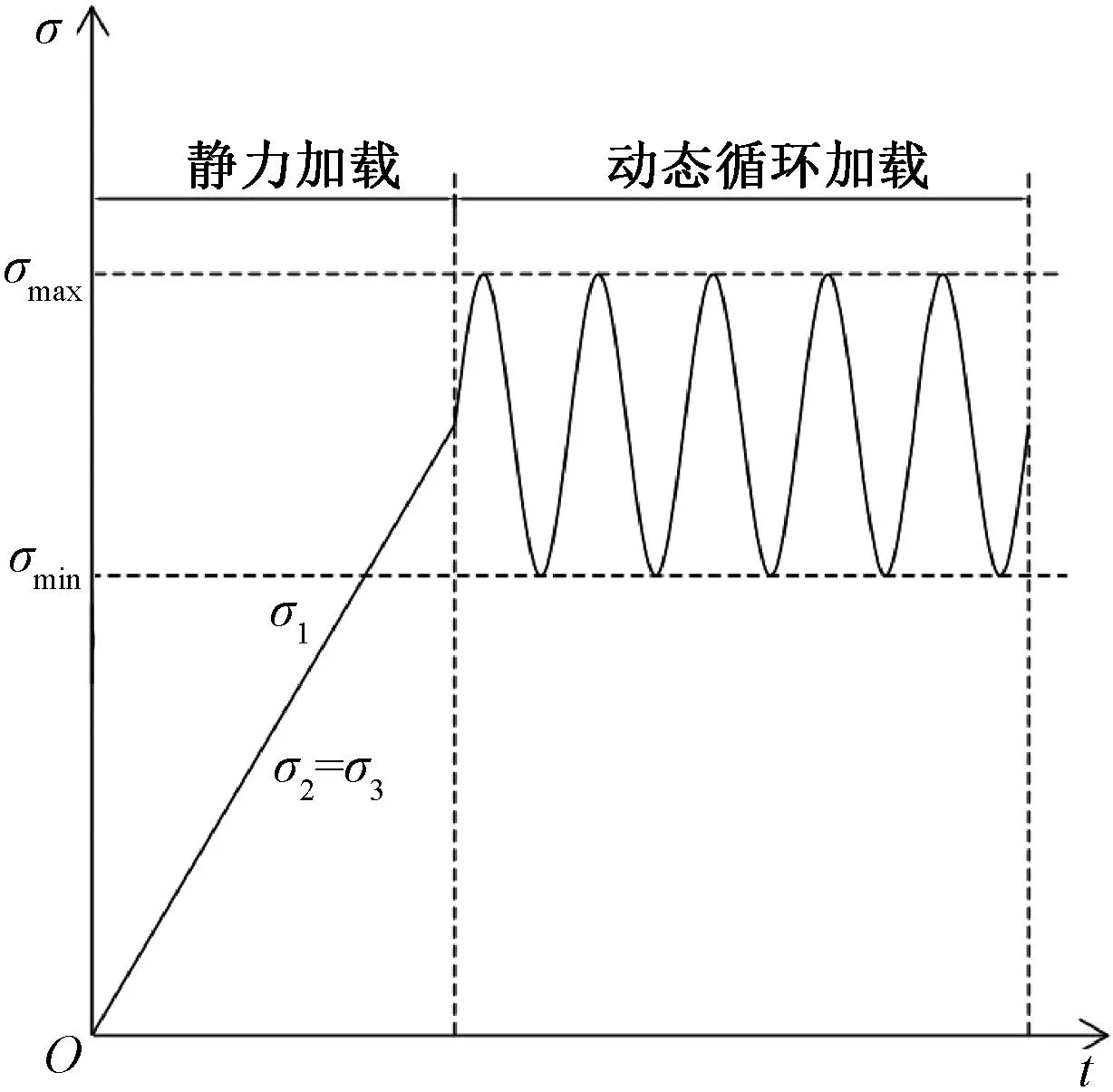
图1 试样加载图Figure 1 Specimen loading

图2 试样破坏对比Figure 2 Comparison of specimen damage

表1 试件命名Table 1 Specimen naming

2 试验数据分析

2.1 围压对岩石动力响应的影响

以动载频率5 Hz试件为例,分析在不同围压下岩石动力响应的变化如图3所示。由图3(a)可知,围压的增大降低了微观裂纹的萌生和扩展所产生的能量,岩石内部的裂隙和孔洞变小,颗粒接触得越紧密,岩石抵抗破坏能力越强、动弹性模量越大。对比文献[13]试验,本次试验所选取的围压范围较大,但两者观察现象一致。

对图3(a)数据进行拟合后可知,斜率和截距的增长幅度逐渐变缓,这是由于在高动应力幅的条件下,一方面岩石内部颗粒的挤压作用更强,动弹性模量增强;而另一方面在内部产生应力集中现象,矿物颗粒发生错动等现象,内部微裂纹逐渐发展,岩石刚度降低,动弹性模量降低。岩石动弹性模量变化是这两方面共同作用的结果,因此岩石的动弹性模量增长缓慢但仍有增长。

由图3(b)可知,岩石动阻尼比随动应力幅增大而降低,且在相同动应力幅下围压较大的动阻尼比比围压较小的低。这是由于高围压抑制了岩石内部裂纹的萌生和扩展,岩石内部微裂纹逐渐闭合,消耗的能量在逐渐减小[14],故在相同应力幅下围压越大的动阻尼越低。

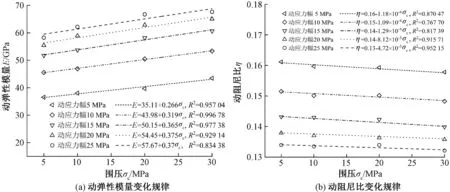
图3 不同围压下动力响应变化规律Figure 3 Variation of dynamic response with different confining pressure

图3(b)数据曲线拟合度随动应力幅增大而增大,在动应力幅较低时,岩石内部活动较为剧烈,所消耗的能量较大,因此曲线拟合度较为不理想;随着动应力幅的增大,岩石内部颗粒逐渐被压密,岩石内部活动剧烈程度变低,因此在较高动应力幅下岩石的曲线拟合度较高。

2.2 动载频率对岩石动力响应的影响

以20 MPa围压试件为例,在不同动载频率下岩石动力响应的变化规律如图4所示。由图4(a)可知,随着动载频率的增大,岩石的动弹性模量增大,增大幅度也增大。一方面,随着动载频率的增大,岩石内部矿物颗粒进行重分布,在颗粒调整位置的过程中,岩石内部产生的小颗粒掉入岩石的微观裂纹中,产生了楔入的愈合效应,可促使裂纹闭合[15];另一方面,随着动载频率的增大,颗粒间流体的黏性增强,颗粒间活动的阻力增大。可见动载频率对动弹性模量的影响十分显著。对比文献[15]、文献[7]的试验,本次试验得到的岩石动弹性模量变化趋势较为剧烈。

由图4(b)可知,在不同动载频率下,岩石动阻尼比都随动应力幅的增大而减小。动载频率增大,岩石内部矿物颗粒与颗粒、流体间的黏滞阻力增大,高频下岩石矿物颗粒需要消耗更多能量发生位移。因此,在相同的动应力幅下高频使得岩石的动阻尼比显著提高。

对图4(b)数据进行拟合,可知岩石动阻尼比随动载频率幂函数增长。这与文献[15]低频条件下的结论是一致的。不同动应力幅下曲线拟合度都很高,表明动阻尼比和动载频率有很强相关性。

2.3 动应力幅对岩石动力响应的影响

动应力幅对岩石动力响应的影响见图5和图6。由图5可知,在相同围压和动载频率下,岩石的动弹性模量均随动应力幅的增大而增大。一方面,在动应力较低时岩石塑性变形突出,内部缺陷逐渐被压密,动应力幅增大会增强岩石内部颗粒的挤压效应,使得岩石刚度提升、动弹性模量增大;另一方面,动应力幅过大会导致岩石内部产生应力集中,矿物颗粒发生错动等现象,岩石内部微观裂纹逐渐发展,刚度降低,动弹性模量降低。岩石动弹性模量受到这两个方面的共同影响,故岩石动弹性模量增长幅度减慢但仍有增长。

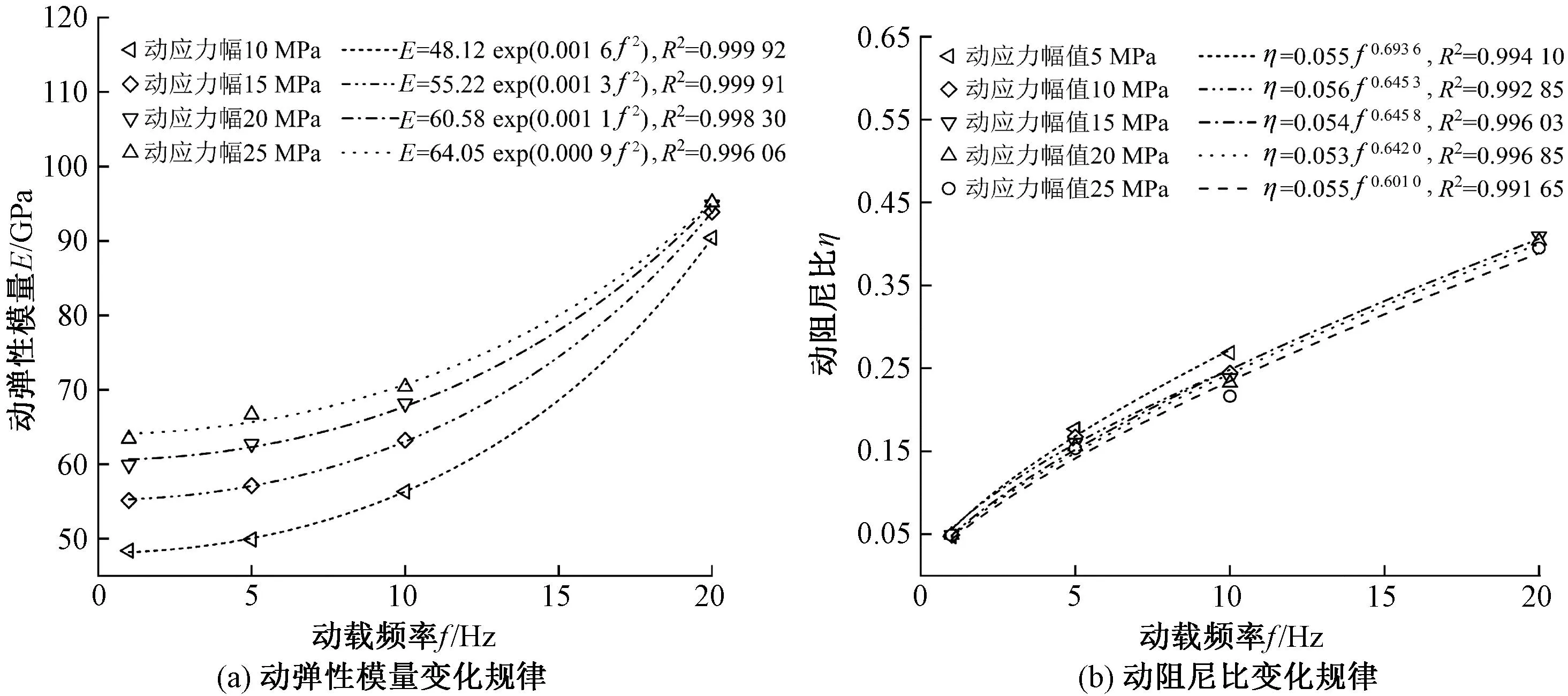
图4 不同动载频率下动力响应变化规律Figure 4 Variation of dynamic response with different dynamic loading frequency

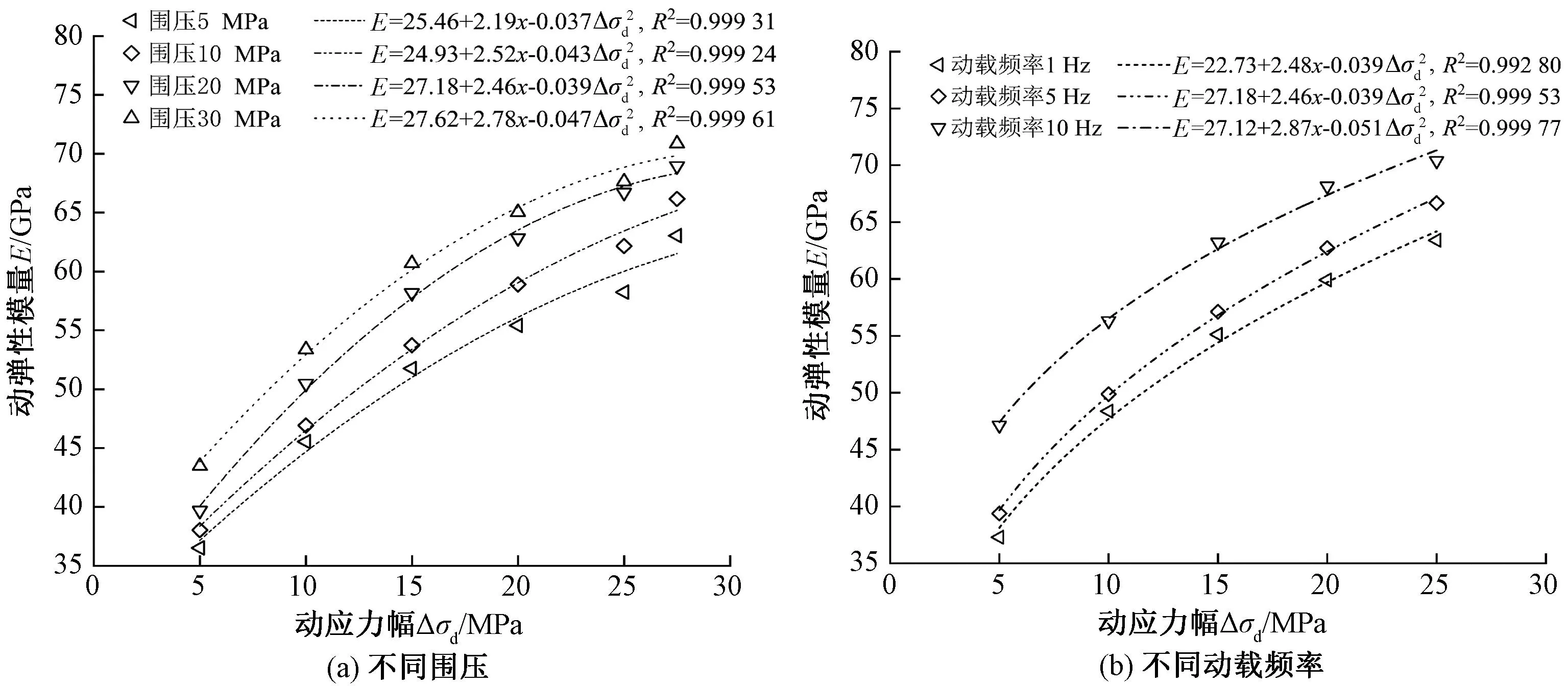
图5 不同动应力幅下动弹性模量变化规律Figure 5 Variation of dynamic elastic modulus with different dynamic stress amplitude

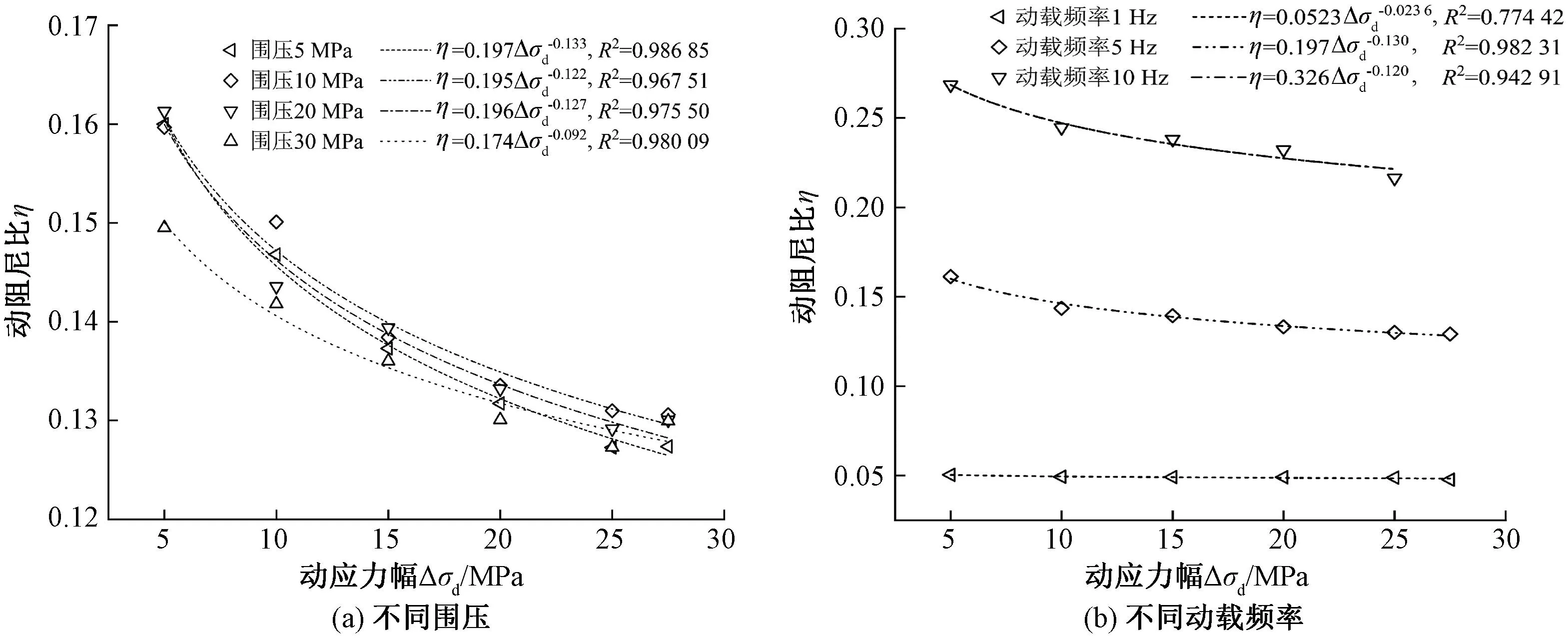
图6 不同动应力幅下动阻尼比变化规律Figure 6 Variation of dynamic damping ratio with different dynamic stress amplitude

由图6可知,随着动应力幅的增大,岩石动阻尼比逐渐减小。这与文献[16]试验所得规律一致,与文献[17]所得规律相反。文献[17]所采用的中风化砂岩属于软岩,本文所采用的花岗岩属于硬岩,因此可以认为岩石本身的材料性质对动力响应也有明显的影响。

对图6中数据进行拟合,可见动载频率相较于围压对花岗岩动阻尼比影响更大。在较高频时岩石内部颗粒没有足够的时间调整到合适的位置,很多小颗粒塌入裂纹中,产生愈合效应[15],因此高频时岩石在不同动应力幅的动阻尼比变化范围减小,曲线拟合度较好。

2.4 循环周次对岩石动力响应的影响

图7为循环周次与动弹性模量的关系图,其中,图7(a)、7(b)的动应力幅分别为5、10 MPa。可以看出,随着循环周次的增加,动态弹性模量呈递减后变缓的趋势,与文献[7]观察到的现象一致。文献[7]所进行的试验循环周次高达800次,在50～100个循环后动弹性模量接近常数。文献[7]的盐岩属于偏软岩,本文的花岗岩属于硬岩,说明增加循环周次会使岩石内部产生塑性变形,循环周次对于不同性质的岩石影响大致相同。

图8绘制了循环周次与动阻尼比的关系图,其中,图8(a)、8(b)的动应力幅分别为5、10 MPa。可以看出,在不同加载频率和围压下动阻尼比随着循环周次的增大总体呈递减趋势。动阻尼比随循环周次的演化规律与文献[12]的结果相似。本文试验中所得动阻尼比变化较为剧烈,但总体呈现L形变化。试验的动应力幅在5～27.5 MPa之间,而文献[12]的动应力幅在90～100 MPa,说明在较高动应力幅和较低动应力幅下花岗岩动阻尼比变化趋势相似。

3 花岗岩本构模型演化

3.1 不同动载频率下岩石本构

利用花岗岩循环荷载试验模拟花岗岩在不同动载频率下的动力特性。图9为试件动应力σd与动应变幅Δεd关系曲线以及Δεd/σd与Δεd关系曲线。由图9 (a)可知,随着动应力的增大,岩石的动应变幅逐渐增大;由图9(b)可知,随着动应变幅的增大,Δεd/σd逐渐减小。由于本次试验的动载频率为1～20 Hz,可认为是准静态加载,因此使用邓肯-张模型进行数据拟合来模拟动应力作用下花岗岩的本构关系,如式(1)、(2)所示,拟合曲线见图9。

图7 不同循环周次下动弹性模量变化规律Figure 7 Variation of dynamic elastic modulus with different number of cycle

图8 不同循环周次下动阻尼比变化规律Figure 8 Variation of dynamic damping ratio with different number of cycle

(1)

(2)

在使用式(2)进行拟合后发现,在动载频率1 Hz和5 Hz时曲线对数据的拟合度较低,不能很好地反映试件在不同频率下的动力响应,于是将邓肯-张模型进行改进,其表达式为

(3)

(4)

式中：a、b、c为模型参数。

图10为改进的本构模型拟合的动应力σd与动应变幅Δεd关系曲线、Δεd/σd与Δεd关系曲线。由图10 (a)可知,随着动应力的增大,试件的动应变幅逐渐增大,曲线拟合效果与图9(a)大致相同;由图10(b)可知,随着动应变幅的增大,Δεd/σd逐渐减小,使用式(4)的拟合效果比使用式(2)的拟合效果要好。可以认为改进后的邓肯-张模型能很好地反映不同动载频率下试件的本构关系。试件模型参数拟合公式如下：

(5)

3.2 不同围压下岩石本构

图11为不同围压下试件动应力σd与动应变幅Δεd关系曲线和Δεd/σd与Δεd关系曲线。由图11(a)可知,随着动应力的增大,岩石的动应变幅值逐渐增大;由图11(b)可知,随着动应变幅的增大,Δεd/σd逐渐减小。使用式(4)对图11(b)的数据拟合发现拟合效果同样达到一个很好的效果,说明改进后的邓肯-张模型也能很好地反映出试件在不同围压下的动力响应。可以认为改进的邓肯-张模型适用于描述不同围压和动载频率下的试件本构关系。试件模型参数拟合公式如下：

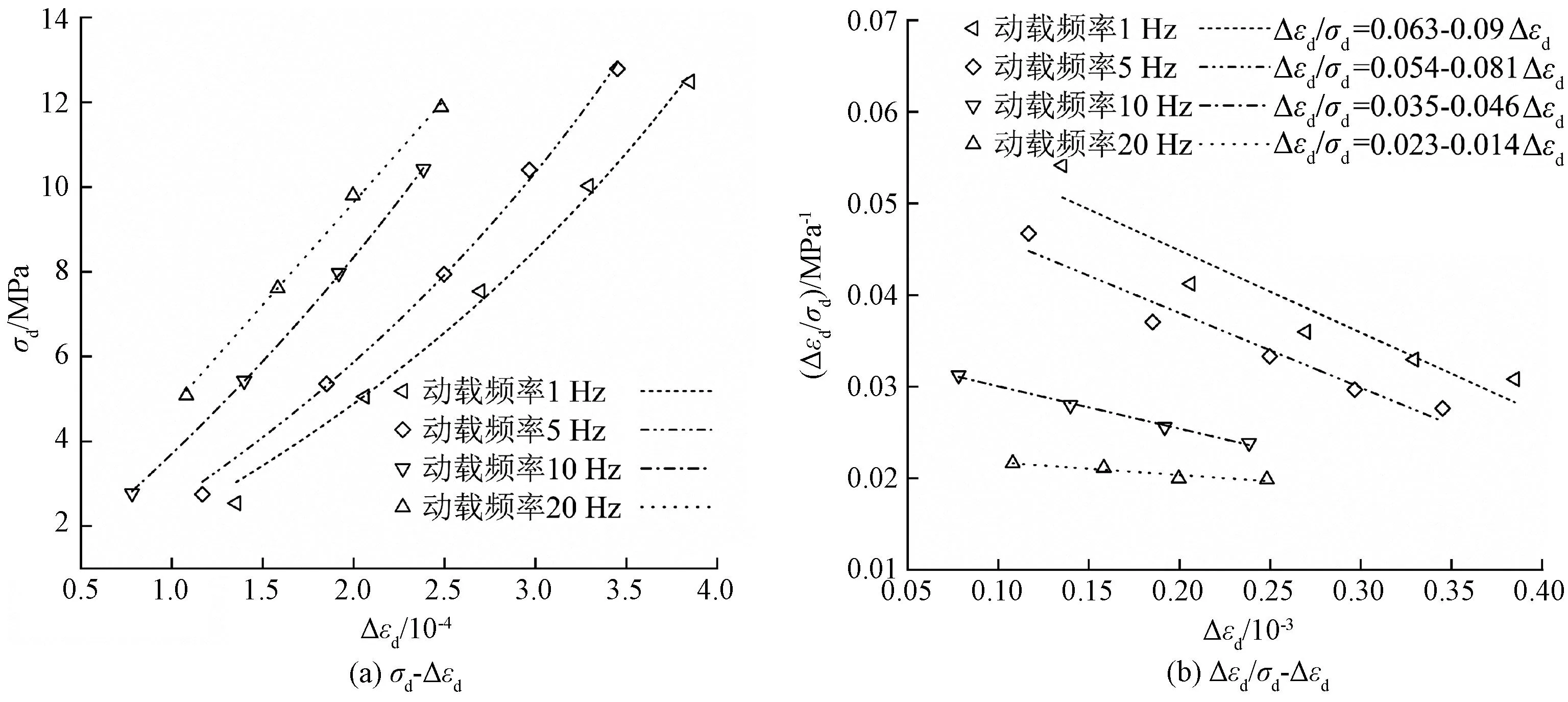
图9 不同动载频率下试件本构模型Figure 9 Constitutive model of the specimen with different dynamic loading frequency

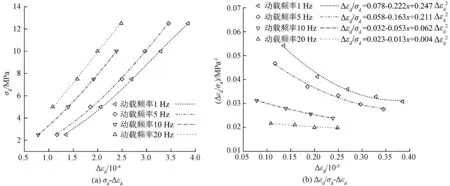
图10 不同动载频率下改进的试件本构模型Figure 10 Improved constitutive model of the specimen with different dynamic loading frequency

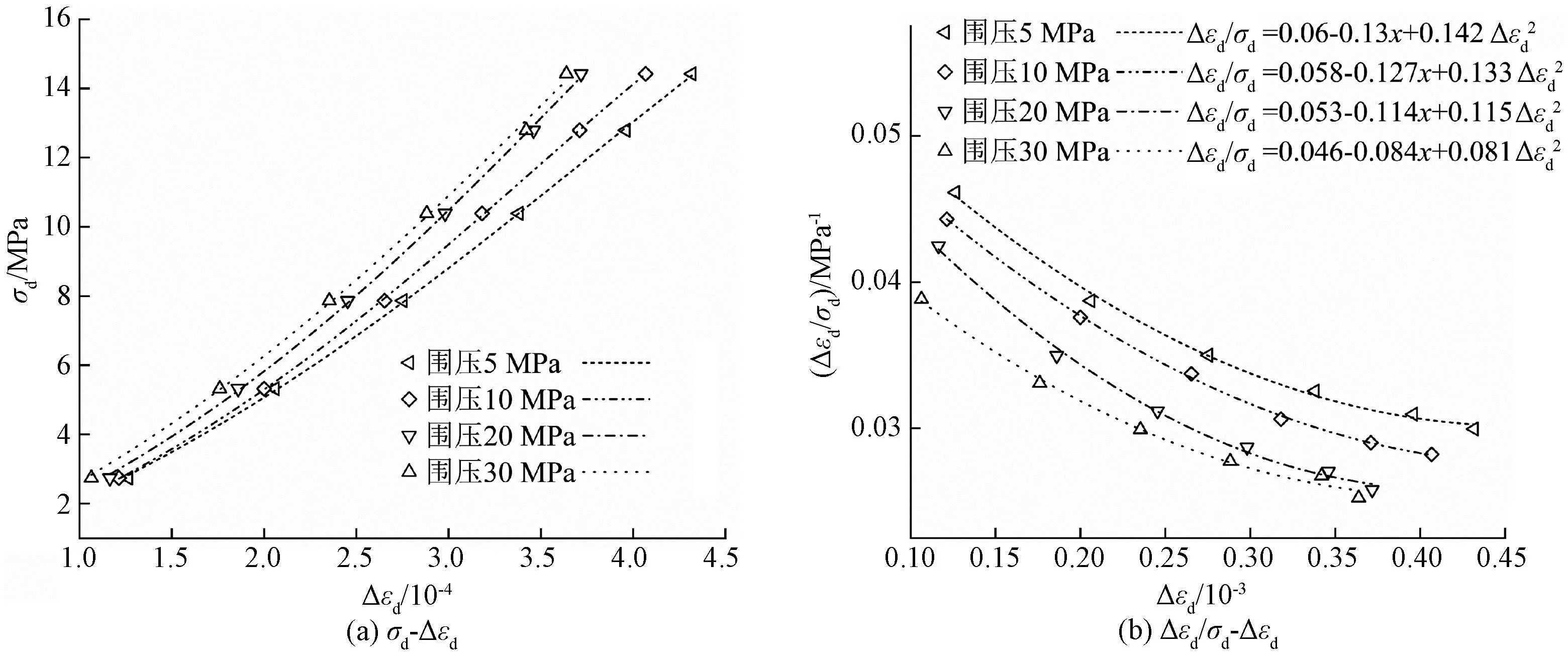
图11 不同围压下改进的试件本构模型Figure 11 Improved constitutive model of the specimen with different confining pressure

(6)

本次试验所得的模型参数表达式即为材料的参数特性,有助于了解不同应力作用下材料参数特性的变化,得到的模型可以为后续动力特性的反演提供参考。

4 结论

通过循环荷载试验,模拟花岗岩在围压的影响下动力特性的变化。试验设置了围压、动应力幅、循环周次以及动载频率1～20 Hz的试验条件,所得结论填补了不同变量以及频率组合下花岗岩动力特性变化的空白,主要结论如下。

(1)花岗岩动弹性模量随围压线性增长,动阻尼比随动弹性模量线性递减,这是因为随着围压的提升岩石内部微裂纹逐渐闭合,消耗的能量在逐渐减小。

(2)花岗岩动弹性模量随动载频率指数增长,这与岩石内部小颗粒与裂纹间产生的楔入的愈合效应和岩石矿物颗粒间黏滞特性有关;动阻尼比随动载频率幂函数增长。

(3)花岗岩动弹性模量随动应力幅二次函数增长,这是由于随着加载的进行岩石内部矿物颗粒逐渐变得密实,岩石的刚度得到提升;动阻尼比随动应力幅幂函数降低。

(4)花岗岩动弹性模量随循环周次幂函数减小;动阻尼比随着循环周次的增加先迅速减小后趋于稳定。

(5)改进邓肯-张模型表达式能很好地描述不同作用条件下花岗岩的本构模型,给出模型参数的表达式可以反演得到不同作用条件下的花岗岩应力状态。