基于中法海洋卫星波谱仪观测的一维海浪谱模型对比*
王义慧 徐星欧 徐 莹
1(中国科学院国家空间科学中心 北京 100190)
2(中国科学院大学 北京 100049)
3(国家卫星海洋应用中心 北京 100081)
0 引言
海浪信息对海气交换、海面观测和仿真等研究十分重要。海浪观测大致可分为浮标观测、光学观测和雷达观测三种。随着遥感技术的兴起,雷达观测使得大面积和全天候的海洋观测成为现实。2018 年10 月29 号中法海洋卫星(China France Oceanography Satellite, CFOSAT)的成功发射预示着海洋的雷达观测进入一个新的阶段[1]。中法海洋卫星能够在全球尺度进行风浪联合观测,其搭载的载荷中,新型微波散射计用以观测海面风场,波谱仪(Surface Waves Investigation and Monitoring, SWIM)用于实现海浪谱的观测。CFOSAT 打开了卫星观测风浪的新局面,不仅有助于深入理解海洋动力过程和变化规律,还在大空间和时间尺度海况模型的建立、气象预报和全球气候变化的研究等方面具有十分重要的意义;而其丰量数据也为海浪谱模型的研究提供了前所未有的重要信息。
海浪谱能反映海浪能量随方向和波数的分布,但已有海浪谱模型大多基于有限的原位测量建立,在适用范围和理论近似上存在局限性。实际海况十分复杂,充分成长条件并非时时满足,现有海浪谱模型与实际海况下海浪能量分布存在差异。本研究基于中法海洋卫星的波谱仪数据,与常用的海浪谱模型:Apel 谱、Elfouhaily 谱和Goda 谱所刻画的海浪能量分布进行对比,分析波谱仪数据的海浪参数观测统计特征与谱模型的差异,以确定常用谱模型与实测海面的具体差异。
1 研究现状
1.1 海浪谱模型
海浪谱的研发见证了人们对海浪的认知和应用的发展。将海浪视为随机过程并用海浪谱描述海浪的历史可追溯到20 世纪50 年代。有研究将无线电噪声理论与海浪应用相结合后,1952 年基于经验的Neumann 谱被提出,该谱得益于简单的结构而被广泛使用。1964 年,基于北大西洋1955 年到1960 年的实测数据,有研究提出了适用于充分成长风浪的PM 谱。1960 年,Wen 等[2]结合能量平衡法和谱方法,提出以圆频率为参量的风浪谱。1968 年到1969年期间,欧美等国家和地区进行了“联合北海波浪计划”(Joint North Sea Wave Project,JONSWAP),有研究根据观测数据提出JONSWAP 谱,用来描述成长中的海浪,该谱具体参数有风区、谱峰升高因子等[2]。1977 年,Yoshimi Goda[3]在JONSWAP 谱基础上进行了改进,以有效波高和谱峰周期作为谱的参数,并对谱峰度因子进行参数化,使其更适应于工程需要。1985 年有研究基于JONSWAP 谱和现场观测,将平衡域频率的指数改为-4,提出了Donelan 谱,用来描述成长状态中的海浪。1989 年有人结合中国近岸特点,引入尖度因子,提出了深水、浅水风浪频谱。1990 年有研究引入谱宽度,提出一个三参量风浪频谱[4]。1994 年Apel[5]提出全波数范围的Apel 谱,该谱在重力毛细波范围(50~1500 rad·m-1)表现良好,并且较好地满足了电磁波与海面作用时后向散射截面的表达,但Apel 谱不满足Cox 和Munk[6]所得的海面均方斜率的结论。1997 年Elfouhaily 等[7]在以往研究的基础上提出了全向波数范围的Elfouhaily风浪谱,Elfouhaily 谱针对以往海浪谱的限制,特别是与Cox 和Munk[6]实验的差异以及谱函数的非解析形式,建立了可以被用来模拟作用于海表的电磁波的分析谱,满足了Cox 和Munk[6]理论。该谱还提出了逆波龄依赖因子,并得出了逆波龄因子和风区的关系。1998 年Karaev 全波数谱被提出,其是一个放射物理(Radiophysical)波谱的形式,2008 年得出谱峰参数γ 的平均值估计为3.3,后续在分析γ 对波浪发展阶段的依赖性时,得出其随着波浪的发展而减小的结论。2018 年Ryabkova 等[8]基于该谱进行修正,使得其可用于模拟浮油中的波纹衰减和计算浮油内部的雷达后向散射截面。Kudryavtsev 谱在1999 年首次被提出,2013 年该谱被新的实验数据修正,风速范围是5~15 m·s-1。风区的取值借鉴了1997 年Elfouhaily谱,长波部分的谱借鉴了Donelan 谱,长短波之间的过渡采用了Elfouhaily 谱相同的指数因子。2004 年Hwang 等[9]基于1984 年提出的风输入源函数的参数化描述了一个全波数曲率谱,2011 年到2015 年该谱被多次修改,在Ku 波段、C 波段、L 波段上有所提高,对50 m·s-1以上的高风速和多种波长范围的电磁波后向散射截面仿真十分有效。后续仍有较多的海浪谱在上述风速条件和谱形等参数修正方面,在已有研究的基础上不断发展。2023 年Guérin 等[10]利用红外大气探测干涉仪(Infrared Atmospheric Sounder Interferometer, IASI)获得波浪斜率的概率密度函数,应用Cox 和Munk[6]的理论,成功获取了真实海面的系列测量,发展了海面的表示模型,但该模型对各个波数之间的相互作用没有表述[10]。
1.2 基于真实孔径雷达的海浪谱观测
随着遥感数据的广泛应用,越来越多的研究开始关注海浪谱的遥感工作,海浪谱的反演也逐渐步入一个新局面。20 世纪80 年代,一些研究提出发射窄脉冲波束的真实孔径雷达探测海浪的想法。1985 年Ku波段雷达海浪波谱仪(Radar Ocean Wave Spectrometer, ROWS)被研制,利用机载谱测量雷达ROWS对海浪谱的遥感理论进行了验证。1992 年欧洲空间局(ESA)与法国空间局(CNES)支持研制对海浪进行观测的C 波段雷达测波仪RESSAC (Radar pour l’Etude du Spectre des Surfaces par Analyse Circulaire),将观测结果与其他海浪观测资料进行比较,获得了较好的一致性。2001 年有研究提出星载波谱仪的构想并研究系统设计参数,并命名为波谱星SWIMSAT (Surface Waves Investigation and Monitoring from SATellite);2003 年开发出C 波段极化雷达观测系统STORM (Système de Télédétection pour l’Observation par Radar de la Mer);2005 年研制出了X 波段相干真实孔径雷达CORAR (Coherent Real Aperture Radar)[11];2010 年Lin 等[12]对星载雷达波谱仪反演海浪谱精度进行了研究,2010 年10 月Song 等[11]利用渤海湾的机载波谱仪数据计算调制谱并进行海浪谱反演。2018 年中法两国合作的项目CFOSAT 发射成功,其上搭载的海洋波谱仪成为第一台实现全球海浪方向谱观测的星载传感器[1]。随着中法海洋卫星波谱仪的成功发射,更多的海浪观测信息被提供,为完善已有的海浪谱提供了条件。
2 SWIM 观测与现有海浪谱模型的对比分析
2.1 SWIM 观测
SWIM 观测可以得到全球海浪方向谱,对于大尺度海域的海洋动力特征研究十分重要[13]。SWIM 是Ku 波段多角度全方位向扫描的真实孔径雷达,其上有6 个旋转脉冲波束:0°,2°,4°,6°,8°,10°,小入射角下,散射机制主要以准镜面散射为主。0°波束以高度计的形式提供风浪参数,6°,8°和10°提供海浪方向谱,SWIM 观测几何如图1 所示[14]。SWIM 可以提供包括风浪和涌浪系统在内的波的能量方向分布。虽然合成孔径雷达(Synthetic Aperture Radar, SAR)也提供海浪谱遥感观测,但SAR 存在频繁的失真效应;且由于速度聚束效应相关的非线性成像机制,只能探测到涌浪系统,即波长大于200 m 的不再受局地风影响的长波系统[15]。与SAR 相比,SWIM 不受速度聚束效应的影响,风浪探测所受约束更小,可以解析更宽的波长范围(从30~600 m)的波的特性。

图1 SWIM 观测几何示例Fig. 1 Geometry of SWIM observation
SWIM 测量的可靠性已经过多方验证。2021 年Hauser[14]用SWIM 数据的海浪谱与模式谱比较,结果表示SWIM 10°波束观测所得海浪谱和海浪参数与模式谱和实测数据的一致性最好,SWIM10°入射角对应的波浪参数以MFWAM 数据为参考,得到的有效波高偏差为 0.02 m,均方根误差为 0.26 m,谱的传播方向以及谱峰波长的偏差分别为 3.9°和-12.3 m,均方根误差分别为 26°和 33 m[16]。2022 年有研究将SWIM 的平均波高方向谱与浮标在不同海况和海面条件下的平均波高方向谱进行谱级比较,对比结果表明,在中海况和高海况下SWIM 波束在8°和10°入射时提供的波浪方向谱与浮标数据具有较高的一致性[16]。2022 年有研究表明 SWIM 的涌浪系统波高数据比传统的哨兵一号SAR 数据更加精确,SWIM 数据是一个珍贵的方向海浪信息源[17]。因此,SWIM 数据提供了有价值的海浪谱细节、海浪参数信息,是浮标观测数据、其他卫星数据或者模式数据之外的重要海面信息来源。
2.2 海浪参数与海浪谱模型
海浪谱表示海浪能量相对于各组成波波数的分布,海浪方向谱描述波浪能量在波数空间和方向上的分布。海浪谱能给出海浪的外部特征,例如:波高、波长、主波方向、周期、波龄、波陡等。但综合而言,影响海面形态的主要参数为以下三种。
(1)海面风。海面风是海浪的主要能量来源之一,是风浪谱模型的主要参数;风速对海浪谱能量和形状有重要影响。
(2)逆波龄、谱峰波数和有效波高。逆波龄表征海浪发展程度,是海态相关因子;谱峰波数kp为谱能量最大值对应的波数,是海浪谱的统计特征之一,决定谱峰的位置;有效波高是重要的海浪参数,代表海浪谱的能量,也是海态相关因子。有研究根据逆波龄对海态进行分类后研究了实际海况中各种海浪系统的占比,其中涌浪占优的比例为50%,风浪占优的比例仅有5%,剩下45%为混合海态[18]。风浪还可以根据逆波龄继续划分为成熟风浪和充分成长的风浪。
(3)谱宽度和峰度。谱宽度和峰度为谱的形状参数,可以描述海浪谱的尖陡程度,二者描述的意义相反,谱峰度值越大,代表谱越尖陡,与之对应的谱宽度值越小;谱峰度值越小,代表谱越扁宽,与之对应的谱宽度值越大。Merle 等[18]对不同海态的形状参数进行了对比分析,得出谱峰度和宽度的空间分布与海态有关,涌浪形状相对于风浪更加尖陡的结论。
常用海浪谱中,Apel 谱、Elfouhaily 谱和Goda 谱模型在应用中较为广泛。2017 年有研究将Apel 全波数谱作为建立方向谱的基础以研究L 波段的海表电磁散射[19],2015 年有研究表明Yoshimi Goda[3]优化的JONSWAP 谱比高斯模型能更精确地刻画涌浪[20],2022 年有研究将Apel 谱、Elfouhaily 谱等谱模型用于移除海浪多普勒频移对海流反演的影响[21]。本研究选取其作为理论模型代表,对斜率谱、波高谱和曲率谱随风速和形态影响变量的变化进行研究分析。
2.2.1 Apel 谱
Apel 谱为全波数海浪谱[6],其描述了充分成长风浪的波长范围。Apel 谱短波部分信息来自造波实验室的数据,长波部分来自海面浮标测量结果。具体表达式如下:
其中,LPM为Pierson-Moskowitz 形状参数,对应重力波谱部分;Jp为JONSWAP 谱中基于PM 谱提出的谱峰升高因子,是非线性峰值效应表达式,用来描述海浪谱峰波数出现的超射现象;Hi为高频效应的组合,表示毛细波谱部分;ID为波数谱在方位向上积分结果附加函数。形状参数
其中,M/N=1,kp为谱峰波数,kp=g(Ω/u)2,与风速有关,Ω为逆波龄,u为10 m 高处的海面风速,g为重力加速度。Apel 谱中,Ω取值为0.84,以描述充分成长的风浪。谱峰升高因子
式中,γ为峰形参数,指数部分的σ为谱峰中心到两侧的宽度参数。
Apel 谱是充分成长风浪条件下的谱模型,风速是模型的重要变量,在不同风速下,Apel 谱具有不同能量分布,图2 描述了风速范围是3 ~23 m·s-1时,Apel 谱的变化规律。图2(a)为不同风速下的Apel 波高谱,随风速增大,谱的能量值增大;但峰值区域附近、波数约为1~10 rad·m-1之间时,能量随风速的变化非常小,从而使得不同风速的能量值相近。在波数大于10 rad·m-1时,风速的影响再次出现,能量值随风速变大的趋势逐渐明显。此外,谱峰的大小和位置受风速的影响,风速变大,峰值变大,位置左移;同一风速下,能量值先增加,在谱峰波数处达到峰值,再随着波数的增加逐渐减小。图2(b)为Apel 斜率谱,其随风速的变化趋势与(a)中波高谱一致。
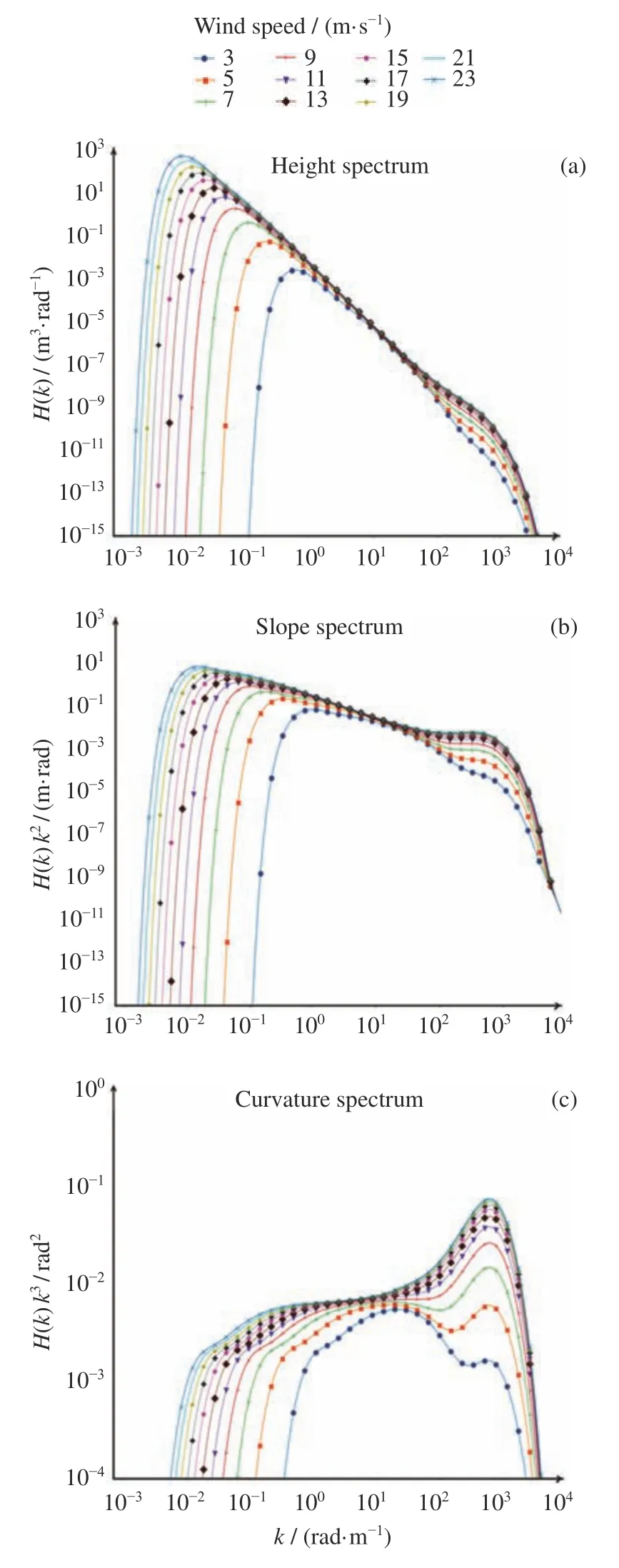
图2 不同风速下的Apel 谱Fig. 2 Apel spectrum at different wind speed
在图2(c)中,Apel 曲率谱随着风速增加,能量值增加,在波数为10 rad·m-1左右,风速影响减小,幅度增加不明显。在不同风速下,第一个能量峰值的波数到10 rad·m-1之间,能量随风速增大而增大,10 rad·m-1到第二个能量峰值的波数之间,能量随着风速增大而增大,大于第二个峰值波数的能量随风速增大而增大。同时,第一个峰值随着风速增大向低波数移动,第二个峰值随着风速增大向高波数移动,两种谱峰值都随风速增大而增大;相同风速下,一条曲线有两个能量峰值,第一个峰值数值在0.1~100 rad·m-1之间,第二个峰值在100~1000 rad·m-1之间。
2.2.2 Elfouhaily 谱
Elfouhaily 谱在一级谱峰到二级谱峰范围内建立了较好的模型,通过JONSWAP 谱公式修正长波区域表示未充分成长的海表,并建立了新的风区与逆波龄的关系,对开阔海域上大风区值进行了扩展。Elfouhaily 谱由两部分组成,Bl代表长波曲率谱,Bh代表短波曲率谱[7]。长波部分在PM 谱和JONSWAP 谱的基础上,引入逆波龄并分析了逆波龄与风区的关系,有
这里X为无量纲风区,能粗略表示海态变化的影响。该谱模型公式如下:
长波曲率谱Bl的表达式为
其中,αp为长波的广义Phillips-Kitaigorodskii 平衡范围参数,其值取决于逆波龄,c为相速度,cp为谱峰处的相速度,Fp为长波边界效应函数,有
式(6)包括三部分,第一部分为LPM,见式(2),其中M/N为1.25;第二部分Jp见式(3),其中γ和σ为逆波龄函数,第三部分为
是一个截止项,对小于10 倍kp处谱的剩余能量进行限制。
短波曲率谱Bh的表达式为
短波部分表达式的物理含义基本与长波相同,αm为短波的广义Phillips-Kitaigorodskii 平衡范围参数,cm为曲率谱中假设的重力毛细波峰值在波数km处的最小相位速度。Fm为短波边界效应函数,有
Elfouhaily 在设定海态下的主要变量为风速,图3描述了Elfouhaily 谱在充分成长风浪条件下,随风速的变化规律,风速范围设置与2.2.1 中对Apel 谱分析的相同。图3(a)~(c)分别为Elfouhaily 高度谱、斜率谱、曲率谱。其曲率谱在不同风速下,随着风速增加,两端波数能量值增加,在波数为10 rad·m-1左右,风速影响减小,能量增加幅度不明显;曲率谱有两个峰值,第一个在波数为0.1~100 rad·m-1之间,是较为平缓的峰值;第二个位于波数范围是100 ~1000 rad·m-1时,是最高的峰值。波数在0.1~100 rad·m-1处,谱的能量在风速高时低于风速低时,这是由于表示长短波间过渡的指数因子,在波数大于10 倍kp处设置了截断点,限制波的能量。这也产生了后向散射截面对风速的非单调依赖[8]。总体而言,与Apel 谱随风速的变化趋势一致。

图3 不同风速下的Elfouhaily 谱Fig. 3 Elfouhaily spectrum at different wind speed
2.2.3 Goda 谱
Goda 谱是1977 年Yoshimi Goda[3]基于工程应用需求在JONSWAP 谱的基础上改进而来的海浪谱。波数范围主要覆盖涌浪,该谱以谱峰周期和有效波高为参数,利用有效波高和谱的0阶矩之间的关系获得谱内的特征系数值,H1/3为有效波高,通过观测得到,m0为总波能的特征值,对波高谱积分求得。该谱的表达形式为
其中,Tp为谱峰周期,γ为谱峰升高因子,σ为峰形因子,其值为
Goda 谱与风速无直接关系,以下根据其主要变量,对谱峰波数kp和有效波高进行分析。图4 是相同kp下Goda 谱随有效波高的变化规律,图5 给出了相同有效波高下,Goda 谱随kp的变化规律。图4(a) ~(c)分别为波高谱,斜率谱和曲率谱,在同一kp下,随有效波高的增加,谱能量值增加。其中(c)图曲率谱中,在波数0.05~0.1 rad·m-1之间出现波谷,对应波高谱和斜率谱表现为谱下降速率变缓。图5 中(a) ~(c)分别是波高谱、斜率谱和曲率谱,在同一有效波高下,随kp增加,谱峰增大且右移,在(a)的波高谱中,谱形状更加扁宽,谱峰能量值逐渐下降。

图4 kp为0.048 rad·m-1 时不同有效波高下的Goda 谱Fig. 4 Goda spectrum at different significant wave height when kp is 0.048 rad·m-1

图5 有效波高为3 m 时不同 kp下的Goda 谱Fig. 5 Goda spectrum at different kp when significant wave height is 3 m
3 SWIM 数据统计特征分布
通过研究SWIM 实测数据的风速、有效波高、谱峰波数,逆波龄、波陡、谱宽度和峰度的统计特征,得到海浪参数的特征分布和平均值,进而对实测海态进行讨论和初步分析。本研究使用2022 年全球范围的中法海洋卫星波谱仪L2 级10°入射角的海浪谱数据进行分析。数据包含全向波数谱和二维波数谱以及有效波高、主波波长、主波波向等参数。为保证实验数据的可靠性,首先去除异常值,筛选出无雨、无陆地掩膜值的纯海表;并获取数据参数均处于置信区间内的海浪观测单元(box,以下简称浪单元);其次,为减小实测数据中虚假峰的影响,筛选出有效波高大于1.2 m 和谱峰波数大于0.001 rad·m-1的浪单元。为便于同上述波谱比较,再筛选出谱峰波数与谱最大值对应波数的差异不超过0.001 rad·m-1的浪单元。最后根据风速分布共初步筛选出119359 个浪单元。
本研究将风速范围作为数据筛选依据之一,设定风速研究范围为2~12 m·s-1。对2022 年SWIM 运行轨道两侧的风速进行了初步统计,同一风速区间在每个月的占比波动较小。图6 是不同风速区间在十二个月份的占比分布统计图,由图6 可知,本研究所用数据观测在同一风速区间12 个月的占比波动不大,0~2,12~14,14~16,16~18 m·s-1和大于18 m·s-1的风速区间在每个月的占比都不超过10%,因此选择风速范围2~12 m·s-1,且不对月份进行区分。

图6 风速分布统计Fig. 6 Statistical result of wind speed distribution
图7 为2022 年的风速分布直方图,由图7 可知,风速分布大致服从韦布尔(Weibull)分布,平均值为7.416 m·s-1。
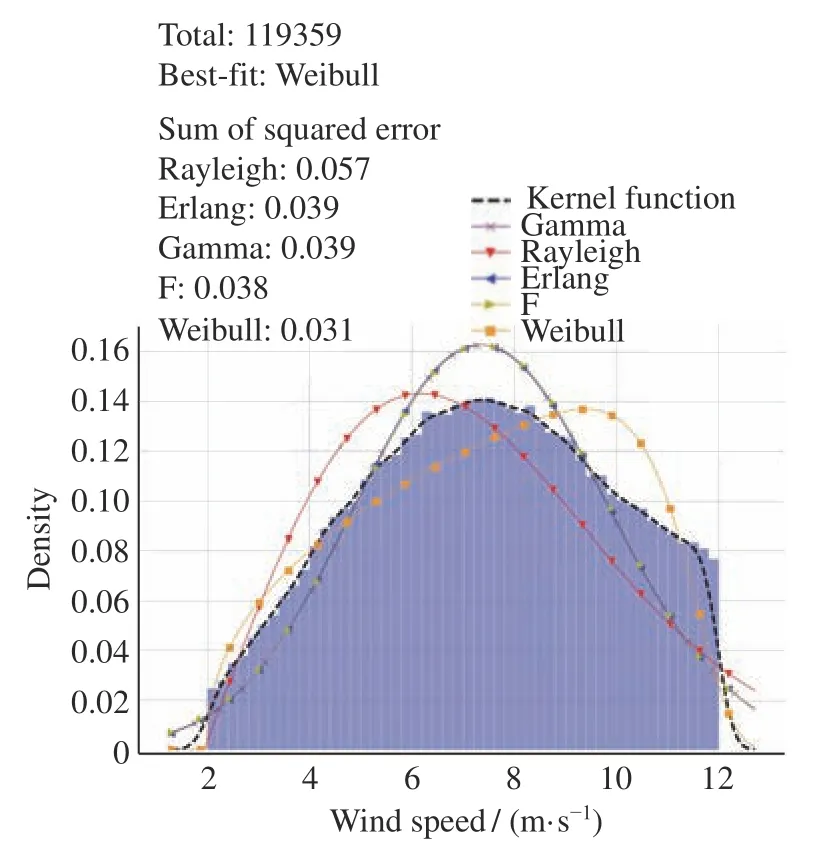
图7 风速直方图Fig. 7 Histogram of wind speed
表1 给出了不同海态海浪参数平均值。由表1最后一行数据可知,逆波龄为0.388,波陡为0.013,表明实际海况涌浪成分居多,风浪大多处于成长中状态,由图8(c)(d)可知波陡和逆波龄呈现韦布尔(Weibull)分布。由图8(a)可知谱峰波数主要集中在0.015~0.04 rad·m-1之间,平均值为0.027 rad·m-1,由图8(b)可知有效波高对于伽马(Gamma)分布、F 分布、埃尔朗(Erlang)分布均拟合较好,平均值为3.087 m。

图8 海浪参数直方图Fig. 8 Histogram of wave parameters
在Merle 等[18]分析SWIM 数据形状特征研究中,采用了谱宽度公式和谱峰度公式,即
其中,F(f)为波高谱,fmin和fmax分别对应实测数据的最小频率和最大频率。图9 为使用SWIM 数据绘制的谱形状参数直方图。图9 (a)为谱宽度直方图,大致服从F 分布,平均值是0.082,图9 (b)为谱峰度直方图,大致服从伽马(Gamma)分布,平均值是2.259,也进一步印证了实测海况中,涌浪成分占主导。
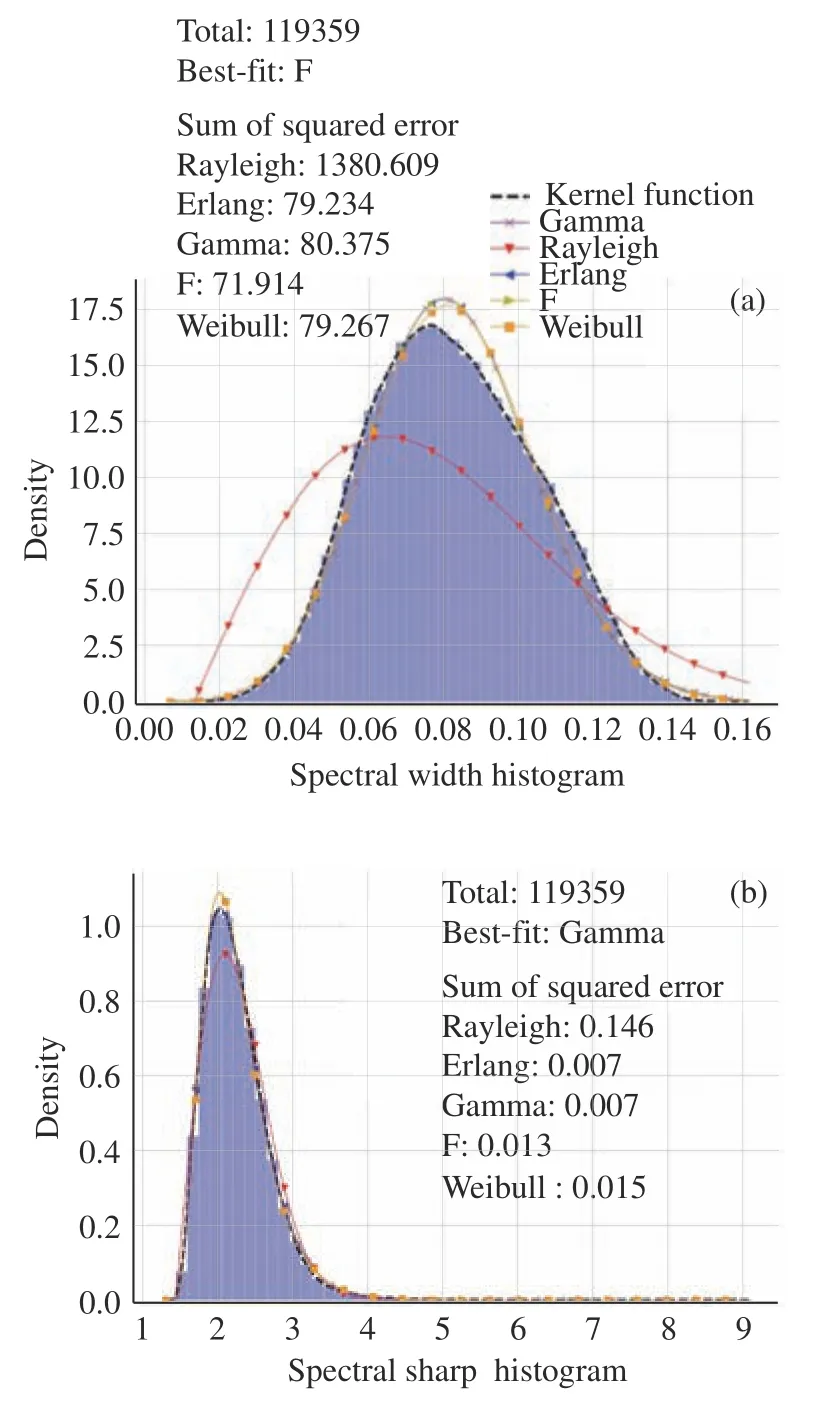
图9 谱形状参数直方图Fig. 9 Histogram of spectral shape parameters
4 SWIM 实测数据与Apel,Elfouhaily,Goda 谱模型的比较
为了分析Apel 谱、Elfouhaily 谱、Goda 谱模型在不同海态中的具体表现,本研究对海态进行分类,根据2022 年Xu 等[16]的研究,选取Hwang[22]在2009年提出浪场表征的标准。具体来说,当η′>3.64×10-3且Ω <0.84时,涌浪占主导;当η*≤3.64×10-3且Ω >0.84时,风浪占主导,即
其中,η′为海表位移均方根ηrms的无量纲参数,ηrms=Hs/4,Hs为有效波高,U10为海表10 m 处的风速,Ω为逆波龄,kp为谱峰波数。本研究将该标准转换为与逆波龄和波陡的关系,涌浪占优时的标准
风浪占优的标准
选取三种逆波龄范围和对应波陡对实测数据的海态进行分类:逆波龄范围为0.8~0.9 的实测数据组成的平均谱表征充分成长的风浪;逆波龄范围为0.9~1.1 的实测数据组成的平均谱表征成熟的风浪;逆波龄<0.8 的实测数据组成的平均谱表征涌浪。对相应的海浪参数进行特征统计,结果列于表1。
将分类后的实测数据与Apel 谱、Elfouhaily 谱和Goda 谱进行比较分析。逆波龄在0.8~0.9 条件下有680 个浪单元,图10 为实测数据平均后的波高谱、曲率谱与三种谱模型的比较,实测数据在较低波数仍然存在虚假峰现象,实测数据的谱峰大于Apel 谱和Elfouhaily 谱,小于Goda 谱,在波高谱谱峰左侧,三种谱模型与实测数据一致性程度较好,在谱峰右侧Elfouhaily 谱偏离程度大;在曲率谱中,实测数据虚假峰被抑制,Elfouhaily 谱和实测谱峰左侧的一致性最好,Apel 谱在谱峰右侧与实测数据最接近,Goda 谱的形状与实测谱峰右侧的波谷一致性较好。

图10 逆波龄为0.8~0.9 时SWIM 数据与Apel 谱、Elfouhaily 谱、Goda 谱的比较Fig. 10 Comparison between SWIM observations and spectrum models, such as Apel, Elfouhaily,Goda spectrum when inverse wave age rank is from 0.8 to 0.9
表2 给出了Apel 谱、Elfouhaily 谱和Goda 谱与实测数据一致性评价指标,分别是均方根误差(RMSE)、确定系数(R-Square) 、偏差指数(DI)。对于逆波龄为0.8~0.9 条件下的波高谱,Apel 谱与实测数据的差异最小,其次是Goda 谱,Elfouhaily 谱一致性最差,Elfouhaily 谱峰与实测数据最接近,但是Elfouhaily 谱谱峰右侧数值与实测数据偏差较大;在曲率谱方面,Apel 谱的曲率谱与实测曲率谱的一致性程度较好,其次是Goda 谱,Elfouhaily 的评价指标最差,Elfouhaily 谱谱峰右侧与实测数据的差异被放大。

表 2 逆波龄为0.8~0.9,SWIM 与Apel 谱、Elfouhaily 谱和Goda 谱的一致性评价指标Table 2 Consistency evaluation indicators for SWIM with Apel spectrum, Elfouhaily spectrum,and Goda spectrum, when inverse wave age rank is from 0.8 to 0.9
逆波龄为0.9~1.1 时,风浪处于成熟状态,有221 个浪单元。图11 为实测数据平均后的波高谱、曲率谱与三种谱模型的比较。在波高谱中,实测数据的虚假峰一直延伸到波数0.04 左右,平均谱峰波数为0.067,Apel 谱和Elfouhaily 谱谱峰位置偏左,谱峰波数小于实测数据,Apel 谱谱峰值与实测接近,Elfouhaily 谱谱峰值远大于实测谱峰,Goda 谱谱峰位置与实测数据一致,谱峰值略大于实测数据;曲率谱中,Goda 谱截至谱峰后的第一波谷之前与实测数据一致性较好,谱峰值略大,波谷以后Goda 谱的上升速度小于实测数据,不如Apel 谱与实测数据的一致性好,Elfouhaily 谱整体偏大。

图11 逆波龄为0.9~1.1 时SWIM 数据与Apel 谱、Elfouhaily 谱、Goda 谱的比较Fig. 11 Comparison between SWIM observations and spectrum models, such as Apel, Elfouhaily,Goda spectrum when inverse wave age rank is 0.9~1.1
表3 是在逆波龄为0.9~1.1 条件下,Apel 谱、Elfouhaily 谱和Goda 谱与实测数据一致性评价指标,分别是RMSE,R-Square,DI 指数。在波高谱方面,Apel 和Goda 谱模型的评价指标相差较小,Elfouhaily 表现最差,三者评价指标均较低,主要原因是谱峰位置的偏移和实测数据虚假峰的出现。具体地,SWIM 数据在较低波数处存在虚假峰,这会导致低波数能量不能被准确表达,谱峰波数不准确等问题,虚假峰出现的原因是SWIM 斜率谱中较低能量的本底噪声被放大,在转换成曲率谱时,低波数的虚假峰能得到抑制。在曲率谱方面,Apel 谱和Goda 谱的曲率谱与实测曲率谱的一致性程度较好, Elfouhaily 的较差。
当逆波龄小于0.8 时,浪单元数目为11459,涌浪成分占主导,图12 为实测数据平均谱,波高谱中,实测数据谱峰波数较小为0.027,谱形较为尖陡,能量集中在谱峰附近,谱峰值较大,Goda 谱与实测平均波高谱在波数小于0.04 rad·m-1处一致性程度较好,波数大于0.04 以后Goda 谱值逐渐低于实测数据,在曲率谱中更为明显;此时Apel 谱和Elfouhaily 谱在谱峰左侧几乎没有数据表征,谱峰波数远大于实测数据。在曲率谱中,Goda 谱在波数大于0.04 以后与实测数据差距逐渐变大,而Elfouhaily 谱与实测数据较为接近,但Elfouhaily 增长速度较快, Apel 谱的增长速度与实测数据接近。

图12 逆波龄<0.8 时,SWIM 数据与Apel 谱、Elfouhaily 谱、Goda 谱的比较Fig. 12 Comparison between SWIM observations and spectrum models, such as Apel, Elfouhaily,Goda spectrum when inverse wave age rank is less than 0.8
表4 给出了逆波龄为小于0.8 条件下Apel 谱、Elfouhaily 谱和Goda 谱与实测数据一致性评价指标,分别是RMSE,R-Square,DI 指数。在波高谱方面,Goda 谱的评价指标最优,Apel 谱和Elfouhaily 谱评价指标相近且表现较差;在曲率谱方面Elfouhaily 谱的评价指标最优,其次是Apel 谱,主要原因是曲率谱将高波数部分Goda 谱与实测数据的差异放大,而Elfouhaily 谱和Apel 谱作为风浪谱,在实测数据高波数部分对风浪有所表征,缩小了实测数据与两者的差距。

表 3 逆波龄为0.9~1.1 时SWIM 与Apel 谱、Elfouhaily 与Goda 谱的一致性评价指标Table 3 Consistency evaluation indicators for SWIM with Apel spectrum, Elfouhaily spectrum,and Goda spectrum, when inverse wave age rank is from 0.9 to 1.1

表 4 逆波龄<0.8,SWIM 与Apel 谱、Elfouhaily 谱和Goda 谱的一致性评价指标Table 4 Consistency evaluation indicators for SWIM with Apel spectrum, Elfouhaily spectrum,and Goda spectrum, when inverse wave age rank is less than 0.8
5 结论
对SWIM 实测海浪谱及其海浪参数进行了统计特征分析,研究其分布特征,并对SWIM 实测数据与Apel,Elfouhaily,Goda 谱的波高谱和曲率谱进行了比较,分析了所选海浪谱模型与实测数据的异同。
研究表明,实际海况较为复杂,通常海面以混合海态为主,这能在SWIM 观测中得到反映。SWIM数据的局限在于观测波数范围较小,对应观测范围为30~600 m 的海浪,缺少对更小尺度风浪的观测。Apel 谱在逆波龄大于0.8 的曲率谱中与实测数据一致性较好,但是作为单一风浪谱,缺少表征涌浪成分的影响项,无法表征复杂的实际海况。Apel 谱是在充分成长的风浪条件下提出,且只有一个风速变量,无法表征涌浪和混合海态。主要表现为整体面积偏小和低波数区无数据表征。Elfouhaily 谱在逆波龄大于0.8 时,存在谱峰右侧数值过大且在风浪曲率谱中存在高波数部分增长过快的特点。但在涌浪主导的条件下,Elfouhaily 曲率谱在高波数部分与实测数据较为贴合,主要原因是相比于其他谱模型,Elfouhaily 谱中谱峰波数右侧的谱值受cp/c项的影响,该项在谱峰右侧始终大于1,并随着波数的增大而增大。虽然Elfouhaily 谱加入JONSWAP 谱中表示超射现象的谱峰升高因子,能一定程度描述成长中风浪,在谱峰处相比于Apel 谱更接近实测数据,但Elfouhaily 谱也无法较好地表征涌浪成分。Goda 谱通过对JONSWAP 谱进行修正,引入有效波高和谱峰波数变量,在谱峰位置和谱峰大小方面与实测数据较为贴合,对涌浪成分和成长中的风浪有较好的刻画。然而,Goda 曲率谱在高波数部分与实测数据差异较大,具体表现为波数大于0.04 rad·m-1以后,曲线上升缓慢,与实测数据差异逐渐增大。造成差异的主要原因是Goda 谱中并未直接引入风速变量,高波数部分缺乏风浪成分的表征,这一现象在曲率谱中被放大。
中法海洋卫星波谱仪观测数据的科学性和可靠性被越来越多的研究证实,创新的风浪联合观测模式为海浪探测提供了更多可能性,本研究对实测数据与理论模型的差异影响项分析将为后续海浪谱模型的修改和完善提供理论支持。
致谢CFOSAT 卫星数据获取自网站:https://osdds.nsoas.org.cn 和https://www.aviso.altimetry.fr/en/missions/current-missions/cfosat.html。感谢国家卫星海洋应用中心和AVISO+网站提供的数据支持。

