基于改进CSM 模型的硬岩掘进机刀盘危险点应力分析方法
刘建琴 ,吴 迪,徐 攀,乔金丽,郭 伟
(1.天津大学机械工程学院,天津 300072;2.天津大学机构理论与装备设计教育部重点实验室,天津 300072;3.河北工业大学土木与交通学院,天津 300401)
随着我国基础建设的推进,地下空间的开发利用得到发展,隧道里程数逐年上升,截至2020 年底,投入运营的铁路总长约为3.7×104km,其中隧道总长约为6 003 km,2020 年新增隧道长为1 589 km,占比26.5%,在建和规划中的铁路隧道共计22 338 km,将在现有隧道里程基础上增长约272.1%[1-2].面对庞大的隧道掘进里程数,掘进机的再制造不仅能填补市场需求,而且可以降低企业施工成本,充分发挥刀盘的剩余价值,减少环境污染和资源浪费.再制造修复技术(如激光熔覆[3]、冷喷涂、堆焊等)的广泛使用使掘进机表现出良好的服役性能,延长了服役寿命,同时再制造技术的研究将会加快其再制造实施进程,会带来巨大的社会效益和经济效益.
刀盘服役载荷的研究主要集中在滚刀破岩,国内外学者做了大量的相关研究,提出了不同的滚刀受力预测模型.早在1965 年,Evans 以挤压破坏为机理,认为滚刀垂直力与滚压岩石的投影面积有关,提出了伊万斯公式[4],随后,Roxborough 等[5]、东北工学院岩石破碎研究室徐小荷等[6]在伊万斯公式的基础上,修正岩石破碎面积,得到不同形式的滚刀载荷计算模型.张照煌等[7]则在盘形滚刀只做平面滚动的假设的基础上,考虑到盘形滚刀在绕自身转轴转动的同时还绕刀盘的旋转轴线旋转,提出了基于空间运动的盘型滚刀侧向力计算公式.
在上述模型建立过程中,认为岩石破坏机理偏向挤压破坏或者剪切破坏单独作用,且侧重预测滚刀垂直力和滚动力,很少涉及侧向力的计算.目前应用广泛的科罗拉多矿业学院(Colorado School of Mines,CSM)模型[8],破岩机理以挤压和剪切破坏共同作用为基础,是综合利用破碎面积和回归统计破碎带压力的方法得出的半理论半经验模型,但该模型没有给出侧向力的预测值,且垂直力和滚动力的预测偏小.Xia等[9]研究了刀盘上滚刀的侧压力变化规律,在回转切削试验机(rotary cutting machine,RCM)实验中发现滚刀刀圈受到很大的侧向力.上述理论和实验为进一步研究滚刀破岩机理及其载荷预测提供了基础.
为弥补CSM 模型缺少计算侧向力的缺陷,孙斌等[10]在CSM 模型基础上,分析滚刀滚入岩体的过程,给出了三向力的预测,侧向力和滚动力误差在10%以内,但垂直力预测值偏小71.6%,模型需要进一步完善.赵海雷等[11]利用贯入度与滚刀直径相差较大的关系,简化了CSM 模型,但没有涉及到侧向力的预测.赵晓旭等[12]利用德纳维-哈登伯格(Denavit-Hartenberg,D-H)矩阵法从滚刀运动角度分析了滚刀侧向力产生的原因,并没有给出侧向力理论计算方式.上述研究表明滚刀三向力的理论计算模型有待进一步完善.
对于刀盘体的危险点研究,由于刀盘作业工况的复杂性,测定各处刀盘应力难度较大,传感器布置一般集中在刀孔或人孔处[13-14],无法直接得到刀盘各处的应力值;另一方面,文献[15-16]研究了刀盘受到倾覆力矩和径向载荷的波动和刀盘载荷的实施预测方法,都没有对刀盘体的应力分布做进一步分析,限制了刀盘载荷研究成果在刀盘危险点和寿命预测上的应用.王鲁琦等[17]研究了刀盘载荷的振动特性,同样没有涉及刀盘危险点的应力分布.上述研究表明,刀盘受载后的危险点应力分布没有直接的测量方法,理论分析存在不足,制约刀盘载荷分析在刀盘寿命分析及其再制造的应用.
针对刀盘载荷分析的需求和滚刀载荷模型存在的缺陷,以及刀盘应力分布研究的局限性,基于CSM模型,考虑滚刀破岩过程中存在的挤压破坏和剪切破坏,提出了包含侧向力预测的改进模型;以单刀载荷为基础,扩展计算滚刀群载荷,并与有限元仿真结合,分析刀盘危险点应力分布,建立了一种刀盘危险点应力获取方法,并进行了对比验证.
1 改进的CSM模型
1.1 滚刀破岩机理
尽管在TBM 施工中,具体的刀盘、滚刀结构和岩体工况有所差异,但是破岩过程是有共性的.在破岩过程中,安装在刀盘前端的滚刀直接接触岩石,随着刀盘的转动与向前掘进,滚刀在围绕刀盘中心旋转和贯入岩体的同时,也会因岩石的作用产生带有滑移的自转,掌子面上的岩石在滚刀滚压下产生不同形式的裂纹,裂纹交汇贯通后,岩石碎片从掌子面上脱落.与此同时,在岩石被破坏的过程中,岩石对滚刀的反作用以垂直力、滚动力和侧向力空间三向力分布在刀圈上,并且反作用力随着滚刀服役时间和空间的变化而随机变化.在滚刀破岩机理中,滚刀滚压作用下的岩石力学响应是研究滚刀-岩石相互作用的关键.结合滚刀破岩过程,在文献[18-20]的基础上,具体分析刀刃所接触的区域岩石破坏类型,得到刀刃接触的岩石区域因挤压产生破坏,刀刃侧面接触的岩石区域产生剪切破坏,由此将岩土分为3 个区域,区域划分如图1 所示.

图1 滚刀破岩区域划分Fig.1 Division of the rock breaking area by the disc cutter
图1 中,破碎区为滚刀滚压作用下直接破碎的区域,以剪切作用为主,过渡区由于滚刀的挤压作用,会产生大量裂纹,一直延伸到不受滚刀作用的岩土区域,两滚刀作用下的过渡区裂纹交汇时,会产生滚刀联合破岩的作用,破碎区域会进一步扩大.
1.2 CSM模型的改进
滚刀破岩的CSM 模型考虑因素全面,包含滚刀结构参数和安装参数、岩石抗压抗拉强度等物理参数,通过滚刀与岩石接触区域应力的积分得到合力,再分解为垂直力与滚动力,但不能预测侧向力.
结合图1 所示的滚刀的剪切区域和挤压作用区域的划分,在CSM 模型的基本形式上,延续模型中提出的破碎区基本压力的假设,假设刀刃侧面岩石剪切破坏区域也存在基本压力,计入滚刀侧面基本压力,以此为基础完善滚刀的载荷计算.
如图2 所示,在原CSM 模型中,滚刀刀刃受岩石挤压破坏产生的力为
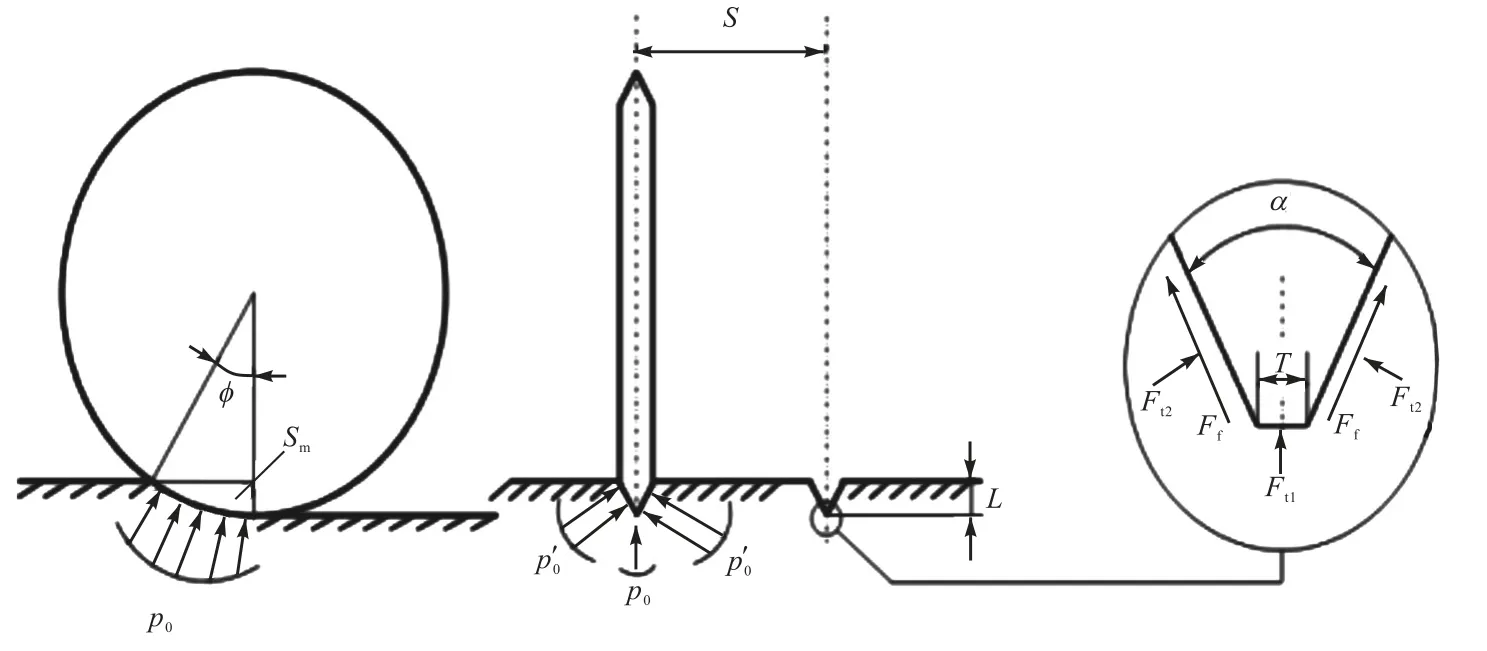
图2 TBM滚刀受力示意Fig.2 Force diagram of the TBM disc cutter
式中:R 为滚刀半径;T 为刀刃宽;φ为滚刀与岩石的接触角,;ψ为刀尖分布系数,− 0.2≤ψ≤0.2;p0为挤压破碎区的基本压力,即
式中:σc为岩石的单轴抗压强度;σt为岩石的单轴抗拉强度;C 为无量纲系数,C≈2.12;S 为滚刀刀尖间距,与刀具的安装有关.
滚刀破岩的分力垂直力 Fv1和滚动力 Fr1表示为
从式(1)~(3)中可以发现,模型并未涉及滚刀刀刃侧面受力计算.而在实际切削过程中,由于滚刀群协同破岩时刀盘受力不均,滚刀受到的侧向力不可能像单刀在线性切割实验中所假定的两侧面力相互抵消,必然会有侧向力的产生.其次,滚刀刀刃呈楔形,在滚刀产生侧向分力的同时,也会有径向分力,进一步衍生垂直力、滚动力分力.考虑滚刀压入岩石的受力状态,在CSM 模型的基础上,从刀刃侧面存在基本压力的假设出发,导出刀刃侧面由于剪切破坏而产生的压力及刀刃侧面与岩石的摩檫力来改进CSM模型.
1.2.1 考虑侧向压力时的三向力计算
图2 为刀刃侧面受压的滚刀受力示意.岩石的剪切破坏面服从摩尔库仑屈服准则[6].经过推导计算得出,刀刃侧面所对的剪切破碎区的基本压力[18]如式(4)所示.
式中:c 为岩石的内聚力;φb为岩石的内摩擦角;β为岩石与滚刀的摩擦角;γ为剪切面与水平面的夹角;α为刀刃角.
滚刀侧面与岩石接触区域在滚刀中性面上的投影为
考虑到滚刀破岩过程中,根本上由于破岩切向力小于滚刀启动扭矩致使滚刀无法自转使滚刀产生偏磨,具体表现为刀刃两侧与岩石不能同时完全接触.由于这种偏磨现象的出现,假定一边侧面接触面积随滚刀的作业状态变化,另一侧面与岩石完全接触,定义面积接触系数 rS表示刀刃两侧与岩石接触的面积之比,即0≤ rS≤ 1.rS=1表示两侧面全接触;rS=0表示两侧面中的一个侧面未接触.当为线性切削实验时,侧向力基本可以抵消,即这里定义的接触面积比 rS=1.
对应到滚刀侧面与岩石接触的总面积为
对应侧面在滚刀径向上的投影面积为
进一步有滚刀刀刃受到岩石剪切破坏而产生的力为
考虑侧向压力时,对应产生的垂直力 Fv2、滚动力 Fr2和侧向力 Fs1分别为
1.2.2 引入刀刃侧面摩擦力产生的三向力
滚刀刀刃侧面产生的摩擦力为
式中μ为滚刀与岩石接触的摩擦系数.
引入刀刃侧面摩擦力对应产生的垂直力、滚动力和侧向力分别为
1.2.3 改进后的CSM 模型三向力
综合式(2)、(3)、(9)、(11)对滚刀受载的分析,得到改进后的CSM 模型垂直力 Fv、滚动力 Fr和侧向力 Fs的表达式为
1.2.4 模型改进效果对比
观察CSM 模型和改进的CSM 模型的公式,对照得出如下结论:改进的模型在预测垂直力和侧向力上的预测公式涉及到的参数更多,考虑因素更加全面;同时弥补了CSM 模型不能预测侧向力的缺陷,但是在侧向力的预测精度上有待进一步探索.
1.3 改进的CSM模型的验证
在科罗拉多线性切割实验台进行滚刀切割科罗拉多红花岗岩的实验,所用的刀具是Robins 公司生产的刀尖宽度为13 mm(D=2 R=432 mm、α=26°)17 英寸(43.18 cm)近似常截面盘形滚刀.实验所用的科罗拉多红花岗岩的单轴抗压强度为158 MPa、单轴抗拉强度为6.78 MPa、内聚力为27.9 MPa.花岗岩的摩擦系数为0.7,故其内摩擦角为35°.表1 为文献[18]整理得到的参数.
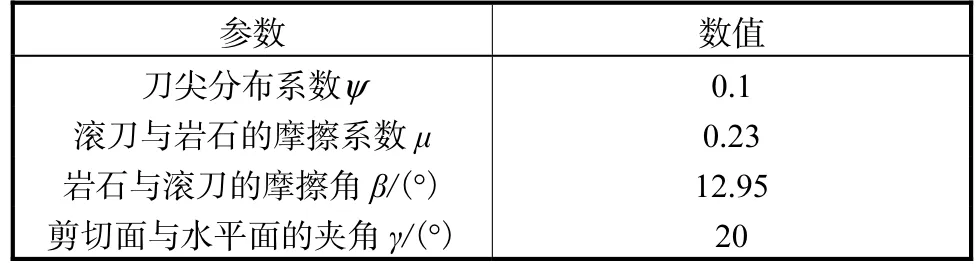
表1 实验数据中的参数Tab.1 Parameters in experimental data
图3 为刀间距为76 mm、不同贯入度(贯入度L的具体取值分别是1.9 mm/r、2.5 mm/r、3.2 mm/r、3.8 mm/r、5.1 mm/r、6.4 mm/r、7.6 mm/r)时,三向力的理论计算结果及实验对照图.改进模型三向力误差(垂直力误差4.95%、滚动力误差2.61%、侧向力误差4.23%)与 CSM 模型的预测误差(垂直力误差15.93%、滚动力误差8.65%)相比更加接近实验值,且三向力平均相对误差均在5%以内,并且改进模型给出了侧向力的预测值,这是因为改进模型考虑了滚刀刀刃侧面受到的压力和摩擦力,一方面给出了侧向力计算,另一方面在CSM 模型基础上增加了垂直力和滚动力的分量.从不同贯入度对应预测值的接近程度上看,随着贯入度的增加,滚刀受到的载荷随之增加,这是由于贯入度越大,滚刀受到的岩石反作用的基本压力越大的缘故.当贯入度为5.1 mm/r 时,预测的滚动力和垂直力偏差最小,侧向力的偏差较大,侧向力整体比垂直力小一个数量级,偏差相对于垂直力和滚动力可认为是小值,说明改进模型对于滚刀载荷的预测精度随着工况的变化会发生波动.由以上对预测结果的分析可以得到,考虑滚刀刃侧面受力的改进模型不仅给出了侧向力的计算方式,整体上也提升了滚动力和垂直力的预测精度,并且其预测精度随着工况的变化会发生小范围波动.

图3 滚刀三向力计算结果对比Fig.3 Calculation result comparison of the disc cutter three-way force
2 刀盘危险点分布及其载荷分析
2.1 刀盘滚刀载荷扩展计算
分析刀盘的危险点,刀盘的载荷输入是关键,目前暂时没有实时的载荷获取方式,采取室内滚刀切削实验的方式成本较高,全刀盘的滚刀载荷仿真耗时较长,故本文采取单刀破岩的方式进行仿真,然后借助改进的CSM 模型扩展至全刀盘.
以辽宁大伙房水库引水隧道工程中MB264-311-8030 mm 型TBM 刀盘为例[21-22].以刀盘滚刀安装数据为基础,以图3 中贯入度为5.1 mm/r 为例,扩展得到各滚刀载荷如表2 所示,作为刀盘危险点分析的输入载荷.
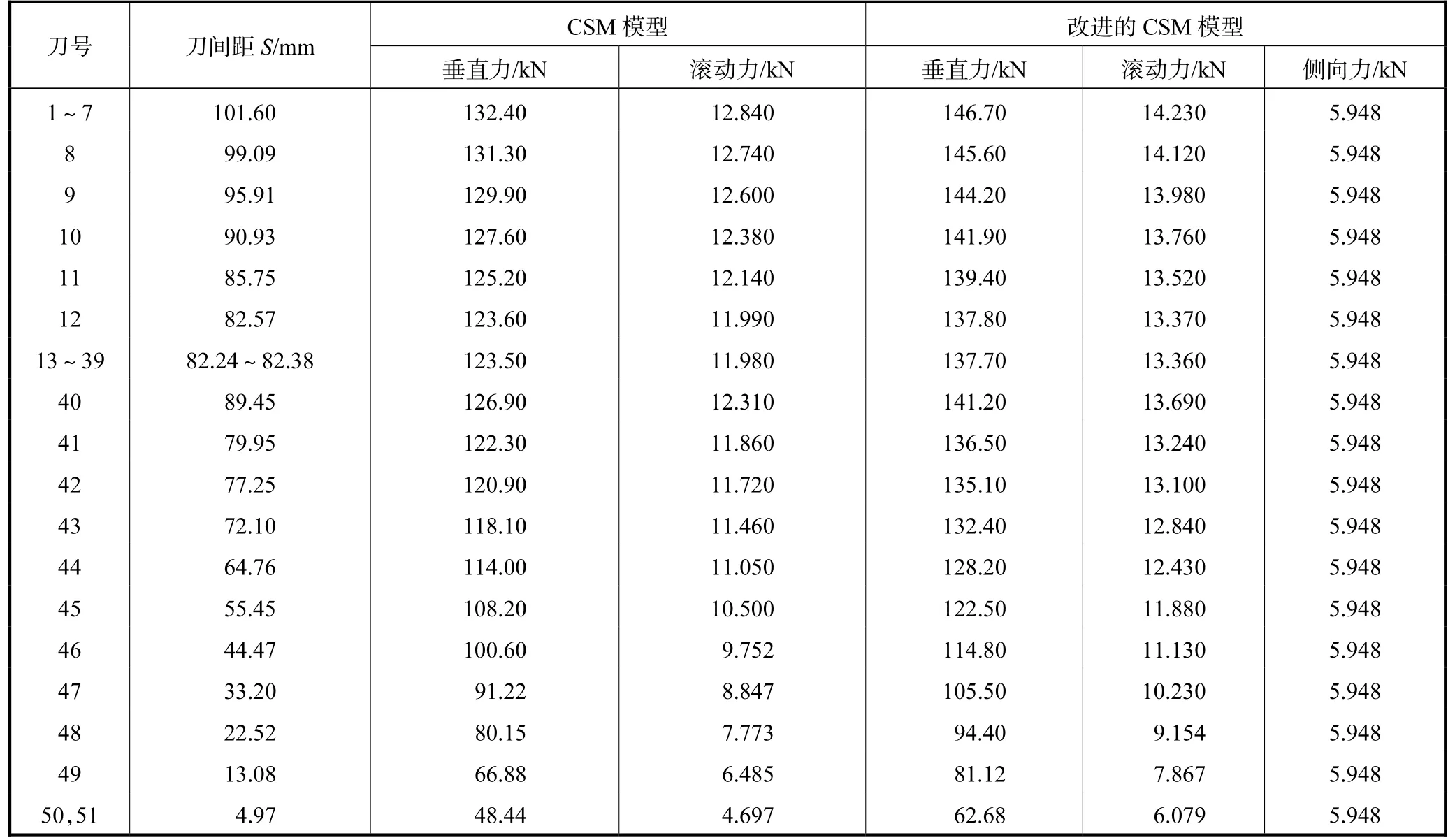
表2 CSM模型与改进的CSM模型的载荷分布对比数据Tab.2 Load distribution comparison data of the CSM model and improved CSM model
2.2 刀盘载荷加载及其分析
TBM 掘进过程中,刀盘受到的载荷源有2 个:一是刀盘的驱动系统;二是岩土与刀盘的相互作用.破岩过程中大部分载荷经由滚刀传递到刀盘.考虑到刀盘整体掘进速度相较于滚刀的滚动速度较小,载荷变化慢,为简化分析刀盘载荷,将刀盘驱动系统的作用视为对刀盘的固定支撑,岩土对刀盘的作用仅考虑变化较大的滚刀载荷对刀盘的影响.
刀盘的加载模型如图4 所示,整体结构为五分体结构,为提高后处理的运算速度,略去刀盘上如筋条、耐磨板、先行刀等非主要结构,刀盘各分体之间用绑定约束来固定,使用ABAQUS 的实体耦合功能,将滚刀孔的各表面与滚刀中心耦合,将表2 得到的各滚刀载荷分别加载在对应的滚刀中心上,分盘的盘体材料参数[23]如表3 所示,经后处理运算得到刀盘的应力云图,分析整个刀盘的载荷分布,进一步获得刀盘危险点的位置如图5(a)中云图色块分布所示.

表3 刀盘盘体的材料属性参数Tab.3 Material property parameters of the cutter head body

图4 刀盘三维加载模型Fig.4 Three-dimensional load model of the cutter head

图5 刀盘的应力分布云图Fig.5 Stress distribution nephogram of the cutter head
对比分析图5(b)中刀盘危险点编号与文献[23]的刀盘危险点统计,共同结果如表4 所示,高应力分布区域与危险点分布一致,位于分体结合处、底部隔板、中心块面板等区域,得到刀盘危险点的载荷大小,可为研究刀盘危险点的寿命提供载荷基础.

表4 滚刀裂纹区域划分Tab.4 Disc cutter crack area division
3 结 论
围绕TBM 刀盘危险点应力分布研究,改进了CSM 刀盘载荷计算模型,并通过单刀载荷扩展计算了全刀盘的滚刀载荷,获取了危险点的应力分布,主要结论如下.
(1) 改进了CSM 模型.分析了滚刀破岩机理,岩石在滚刀滚压下因挤压和剪切共同作用而产生破坏,在此基础上,定义滚刀与岩石的面积接触系数,推导了考虑侧面压力和摩擦的CSM 模型,得到了更为精确的滚刀载荷预测模型,预测的垂直力、滚动力和侧向力的平均相对误差缩小到5%以内,弥补了原CSM 模型不能预测侧向力的不足.
(2) 提出并验证了TBM 刀盘危险点应力获取方法的有效性.使用改进的CSM 模型计算刀盘的扩展载荷,以辽宁大伙房水库引水隧道工程中的MB264-311-8030 mm 型TBM 刀盘为例,应用理论扩展计算和有限元仿真相结合的方式,计算得到了刀盘危险点的Mises 应力分布,通过与刀盘危险点的统计结果对比,发现高应力分布区域与危险点分布一致,位于分体结合处、底部隔板、中心块面板等区域,验证了基于改进CSM 模型的TBM 刀盘危险点应力获取方法的有效性,为刀盘载荷分析在刀盘寿命分析及其再制造的应用提供了指导.
——分清“主”和“次”

