Wavelet Multi-Resolution Interpolation Galerkin Method for Linear Singularly Perturbed Boundary Value Problems

Jiaqun Wang ,Guanxu Pan ,Youhe Zhou and Xiaojing Liu,★

1School of Management Science and Engineering,Anhui University of Finance and Economics,Bengbu,233030,China

2Key Laboratory of Mechanics on Disaster and Environment in Western China,The Ministry of Education,College of Civil Engineering and Mechanics,Lanzhou University,Lanzhou,730000,China

ABSTRACT In this study,a wavelet multi-resolution interpolation Galerkin method (WMIGM) is proposed to solve linear singularly perturbed boundary value problems.Unlike conventional wavelet schemes,the proposed algorithm can be readily extended to special node generation techniques,such as the Shishkin node.Such a wavelet method allows a high degree of local refinement of the nodal distribution to efficiently capture localized steep gradients.All the shape functions possess the Kronecker delta property,making the imposition of boundary conditions as easy as that in the finite element method.Four numerical examples are studied to demonstrate the validity and accuracy of the proposed wavelet method.The results show that the use of modified Shishkin nodes can significantly reduce numerical oscillation near the boundary layer.Compared with many other methods,the proposed method possesses satisfactory accuracy and efficiency.The theoretical and numerical results demonstrate that the order of the ε-uniform convergence of this wavelet method can reach 5.

KEYWORDS Wavelet multi-resolution interpolation Galerkin;singularly perturbed boundary value problems;mesh-free method;Shishkin node;boundary layer

1 Introduction

The singularly perturbed boundary value problem originates from fluid mechanics and arises in the mathematical modeling of physical engineering problems.In this study,we consider the following second-order singularly perturbed two-point boundary value problem:

whereεis a small perturbation parameter that satisfies 0＜ε≪1,andqis a negative number.A key feature of this problem is the presence of a boundary layer in which the solution undergoes large variations with localized steep gradients asεapproaches zero.We assume thatpis a non-zero parameter,and Eq.(1) features a left-side boundary layer atx=awhenp＞0,and a right-side boundary layer atx=bforp＜0.

The presence of boundary layers makes it challenging to solve singularly perturbed problems using classical numerical methods.Consequently,numerous special schemes have been proposed,including transforming the boundary value problem into an initial value problem [1-3],fitting the finite difference method [4],spline method [5-8],finite element method [9-12],and other methods[13-17].In recent years,algorithms based on layer-adapted meshes have become powerful tools for solving singular perturbation problems[18-20],such as the Shishkin mesh[7,21-23]and Bakhvalov mesh[24-27].

Over recent decades,meshfree methods that rely only on nodes to make approximations have attracted considerable research interest[28-32].As pointed out by Li et al.[28],meshfree methods are not only complementary to conventional finite element methods,but they also offer several advantages over mesh-based methods.These advantages include the utilization of higher-order continuous shape functions and the elimination of sensitivity to mesh alignment[31,33,34].Currently,meshfree methods are widely used for solving singularly perturbed boundary value problems because they can quickly obtain more satisfactory numerical solutions by adding extra approximation nodes in the boundary layer.For example,Shen[35]proposed a local radial basis function(RBF)-based differential quadrature collocation method to solve the singularly perturbed two-point boundary value problem,which avoids highly ill-conditioned dense interpolation matrices.Although that study only discussed uniformly distributed nodes,numerical results showed that the local RBF-based collocation method is more accurate and efficient than the globally supported method.The collocation methods are known for being efficient as no integration is required,but they are less stable and accurate.To reduce errors in the standard element-free Galerkin method near the boundary layer,Zhang et al.[36]proposed the variational multiscale element-free Galerkin method to obtain the numerical solutions of convection-diffusion-reaction equations.Numerical results showed that their method is considerably more accurate than the standard element-free Galerkin method,although slight spurious oscillations persisted near the boundary layer.Zhang et al.[37]later presented a novel adaptive algorithm based on the variational multiscale element-free Galerkin method to overcome this drawback.Although many credible results have been obtained using the aforementioned meshfree methods,they still possess some shortages,such as difficulty in imposing of essential boundary conditions and calculating integrals owing to their shape functions are rational functions and lacking the Kronecker delta property[31].

Wavelet-based methods have gained increasing attention as they are widely and successfully used in practical applications [38-42].Numerical methods based on wavelets can be divided into three main categories:wavelet finite element[39-40,43],wavelet collocation[44-48],and wavelet Galerkin methods [49-53].Although wavelet finite element methods have advantages over traditional finite element methods,they still suffer from the same disadvantages in the presence of meshes.Existing wavelet meshfree methods do not require meshes,but they do not guarantee accurate interpolations on non-uniform nodes.

Recently,we proposed a truly meshfree method based on wavelet multiresolution analysis,known as the wavelet multiresolution interpolation Galerkin method (WMIGM) [54,55].Compared with current meshfree methods,WMIGM possesses several advantages[54,55]:

(1) The proposed wavelet multiresolution interpolation formula possesses the Kronecker delta function property;

(2) Polynomial reproduction can be achieved up toγ-1 degrees,expressed as linear combinations of shape functions;

(3) It does not require matrix inversions or ad-hoc parameters;

(4) The stiffness matrix can be efficiently obtained with an analytical integration method.

A key challenge to solving singularly perturbed boundary value problems is dealing with their singularity,which can lead to numerical instability,oscillations,and spurious solutions[20].Moreover,the use of uniform nodes in singularly perturbed boundary value problems results in a significant waste of computational effort,as a sufficiently fine mesh is required to accurately capture the rapid variations of the solution near the boundary layer.Therefore,there is a critical need to develop a more efficient,accurate,and stable numerical method specifically designed for solving such problems.The purpose of this study is to employ the WMIGM to solve linear singularly perturbed two-point boundary value problems (see Eq.(1)) based on special segmented equidistant (Shishkin) nodes.A coarse mesh is utilized in the smooth region,and a fine mesh is applied in the boundary layer.Compared with other meshfree methods,our WMIGM approach simplifies the imposition of essential boundary conditions due to its interpolation property.Additionally,we present error estimates of the algorithm,even in the absence of analytic expressions for the shape functions.Test problems are then solved using the WMIGM over modified Shishkin nodes.

This paper is organized as follows.In Section 2,we review the construction of wavelet multiresolution interpolations and some properties of shape functions.In Section 3,we introduce the WMIGM scheme for solving linear singularly perturbed boundary value problems.The parameter uniform convergence is explained in Section 4,followed by numerical experiments and comparisons with existing methods in Section 5,which illustrate the accuracy and efficiency of the proposed wavelet method.Finally,concluding remarks are provided in Section 6.

2 Wavelet Multiresolution Interpolation

This section reviews the construction of the wavelet multiresolution interpolation approximation and explains several key properties of the wavelet interpolating shape function that was proposed in our previous works[54,55].

We begin with the interpolating wavelet transform[44,56],as applied to the following dyadic grids on the real line:

wherexj,kare the grid points,a0is a real number,jis the decomposition level,andh0is the spatial step withj=0.By using the linear superposition of the interpolating wavelet transform,a continuous functionf(x)∈L2(R)of the form

Next,we focus on the interpolating wavelet transform construction for interval[a,b]on a set of dyadic grids:

whereh0=(b-a)/n0is the spatial step withj=0,andnj=2jn0is the number of grids at the level of resolutionj,which satisfiesn0≥γ.

By applying Eq.(3)to approximate a continuous functionf(x) ∈L2(R)on the interval[a,b],we obtain

Based on the compact support of the scaling function,Eq.(5)can be rewritten as

It can be seen from Eq.(6) that we require the values of(x) at some external auxiliary points located outside the interval[a,b].Following the work of Donoho[56],the unknown values off(xj,k)fork＜0 ork＞njare obtained with the Lagrange interpolation polynomial of degreeγ.It follows that we may define a new function(x)such that

Substituting Eq.(7)into Eq.(6),we obtain

Notice that the grid points inare regularly spaced.We next introduce multiresolution interpolation[54,55]:

whereN+1 is the total number of nodes in[a,b],and the wavelet multiresolution interpolating shape function(x)can be obtained using the following recurrence relation:

with the following initial condition:

Lemma 2.2([54,55]): The wavelet multiresolution interpolating shape function(x) has the following important properties:

Definition 2.1:is the set of functionsf(x) such that everyf(x) ∈has the following representation:

Lemma 2.3([56]): For functionf(x) ∈L∞([a,b]),the error betweenf(x) andcan be estimated as

whereC1is a constant,depending on the derivatives of(x)andf(x).

3 Description of the WMIGM

In this section,we formulate the WMIGM for singularly perturbed boundary value problems on Shishkin nodes[19].

3.1 Node Generation

We first divide the computational domain[0,1]into two subintervals each for left-and right-side boundary layer problems:the fine part[0,σ],the crude part[σ,1],and the crude part[0,1-σ],the fine part[1-σ,1],respectively.The transition parameter is defined byσ=min{1/2,αεln(N)/|p|},whereα≥γ,andN∈N is the total number of grids.We consider that the number of grid points in each subdomain is equal and that they are uniformly divided;thus the step of the grid in the rough region ishS=2(1-σ)/N,and that in the fine region ishE=2σ/N.Following the recurrence relation of Eq.(12),we have

in whichJis an integer.

In the subsequent calculations,we setσ=1/(2J+1),in whichJ=maxan integer,andαis an integer.Thus,we have

We then evenly arrange the nodes into two subintervals:

for left-side boundary layer problems,and

for right-side boundary layer problems.

After the nodes are generated,we use the iterative formula in Eq.(12) to obtain the wavelet multiresolution interpolating shape functions.Then,the approximation solution ofu(x) can be calculated with Eq.(11).

3.2 WMIGM for Singularly Perturbed Boundary Value Problems

The variational form of Eq.(1)isu(x)∈(0,1),such that

Then,we replace the infinite dimensional space,(0,1),with the wavelet multiresolution interpolation space,and obtain the WMIGM:

Using this process,we can obtain the WMIGM solutions by solving Eq.(23).

4 Error Analysis

In this section,we provide the WMIGM’s error estimate,which relies on the modified Shishkin nodes.In the following analysis,we assume thatεN≥21-αto ensure thatN≥2J+1holds.The solution of Eq.(1) can be decomposed intou=S+E,in whichSis the smooth component andEis the boundary layer component[12,21,57,58],where

Based on the properties of the wavelet multiresolution interpolating shape functions introduced in the previous Section 2,we have the following interpolation error estimates.

Lemma 4.1:Letube the wavelet multiresolution interpolant ofu(x)on the modified Shishkin nodes.Thus,we obtain the properties for

whereCis independent ofNandε,and the energy norm is defined as

Proof:Using a Taylor expansion atxi,the interpolation error of|S(x)-S(x)|forx∈[xi,xi+1]can be rewritten as

Then,from Eqs.(17)and(24),on the boundary layer part,we have

Obviously,Eq.(25)can be easily demonstrated through Eqs.(28)and(30).

Thus,it remains to prove the estimate Eq.(26).From Eq.(24),we get

The estimation of Eq.(26)can then be derived immediately.

Theorem 4.1:Letube the solution of Eq.(1)anduN∈be the WMIGM solution of Eq.(23).Thus,we have

in whichCis independent ofNandε.

Proof:Letξ:=.Applying the Galerkin orthogonality,we get

Owing to the Hölder inequalities and Eq.(26)ofLemma 4.1,it holds that

With the aid of integrating by parts and the Cauchy-Schwarz inequality,we observe that

which is the required result.

5 Numerical Results

In this section,we applied the WMIGM to four examples to evaluate its numerical accuracy.We considered two grid points: uniform node points using the wavelet interpolation Galerkin method(WIGM)and refined local grid points using the WMIGM,as specified in Section 3.If not otherwise specified,γ=6 andα=3.

To estimate the accuracy of the solutions,the maximum absolute andε-uniform errors at the grid points are taken as

and the numerical rates of convergence are

All numerical results were conducted on an AMD Ryzen 7 3700X CPU@3.20 GHz with 64 GB RAM in MATLAB.

5.1 Test Problem 1:Left-Side Boundary Layer Problem

We begin our numerical cases with the following left-side boundary layer problem[6-7,59,60]:

The boundary conditions are extracted from the exact solution as

The absolute errors obtained by the proposed WIGM withN=100 for different values ofεare presented in Fig.1.The numerical results show that the errors are mainly located near the left-side boundary layer,and they increase with the decrease ofε.In Table 1,we list the maximum absolute errors and computational orders of convergence on uniform points using the WIGM and non-uniform points using the WMIGM for different values ofεand grid pointsNwithγ=6.From Table 1,we find that the numerical solutions obtained by the WMIGM are much better than those computed by the WIGM,especially forε→0.In particular,WMIGM using 256 grid points exhibits slightly better accuracy than the WIGM using 512 nodes forε=2-5andε=2-6.Therefore,solution accuracy can be improved by adding local nodes in the boundary layer.Moreover,a comparison of the numerical errors obtained by the WIGM,the WMIGM,the quintic B-spline method (QBSM) with Shishkin mesh[6],and the novel optimal B-spline(NOBS)technique with Shishkin mesh[7]is also illustrated in Table 1.There,it can be seen that for most cases,the WMIGM is more accurate than the QBSM and the NOBS,given the same number of grid points for most cases listed.The numerical solutions obtained by the WIGM and the WMIGM are shown in Fig.2 with the corresponding exact solution forε=2-9.Note that the WMIGM withN=64 can achieve nearly the same accuracy as the analytical solution,whereas the WIGM does not converge at smallεvalues.To visualize the convergence ratio of the proposed algorithm,Fig.3 displays the error norm as a function of the number of grid points withε=2-7.It can be seen that the proposed WMIGM’s convergence rate ofEε(N)is approximatelyγ-1 forNε≥2-2,which is consistent with the previous error analysis.Moreover,the curves visually demonstrate that our results are better than the QBSM and the NOBS,and the numerical convergence rate of the maximum errorEmaxis approximatelyγ.Notably,the results of the WMIGM withγ=6 are quite bad forN=32,as shown in Table 1.We conclude that is due to the support domains of the shape functions will become larger asγincreases.Thus,we need more sampling points to capture the local large gradient information for a largeγ.We can see that this phenomenon does not occur whenγ=4.

5.2 Test Problem 2:Left-Side Boundary Layer Problem

We next consider a source-free singularly perturbed problem as described in[3,10,60-62]:

whose analytical solution is given by

in whichm1=.The solutionu(x)satisfies the boundary conditions ofu(0)=1 andu(1)=1.

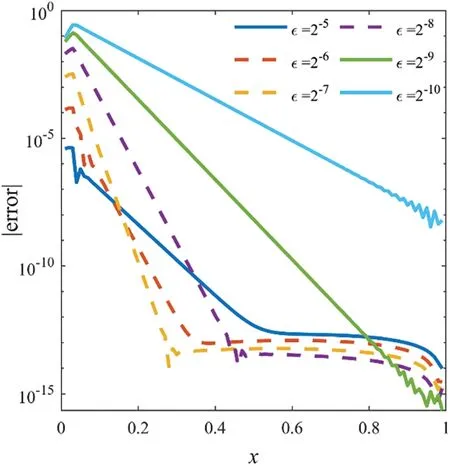
Figure 1:Absolute errors of WIGM for Example 1 with N=100

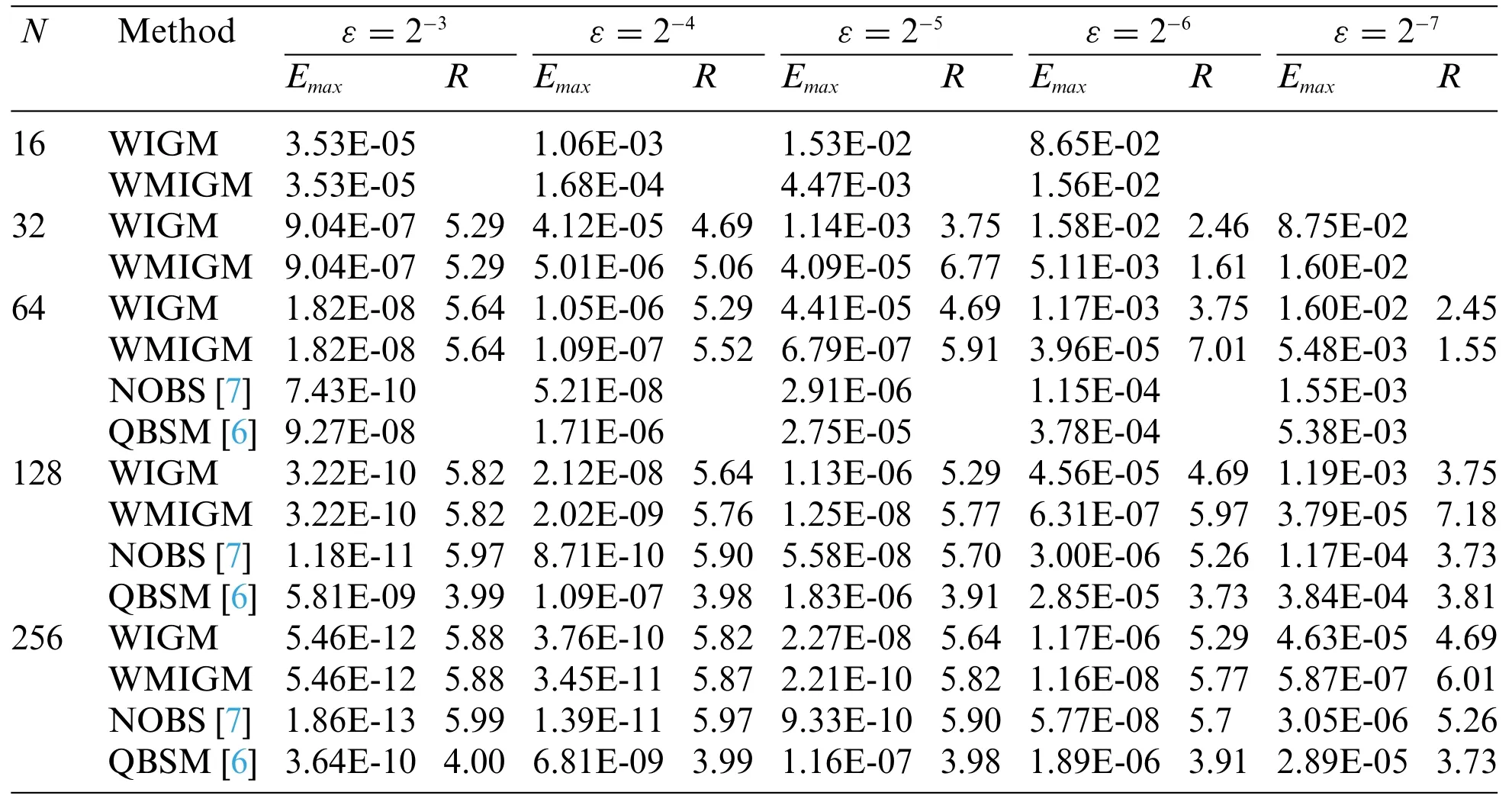
Table 1:Maximum absolute errors and convergence rate of Example 1 for different values of ε and N

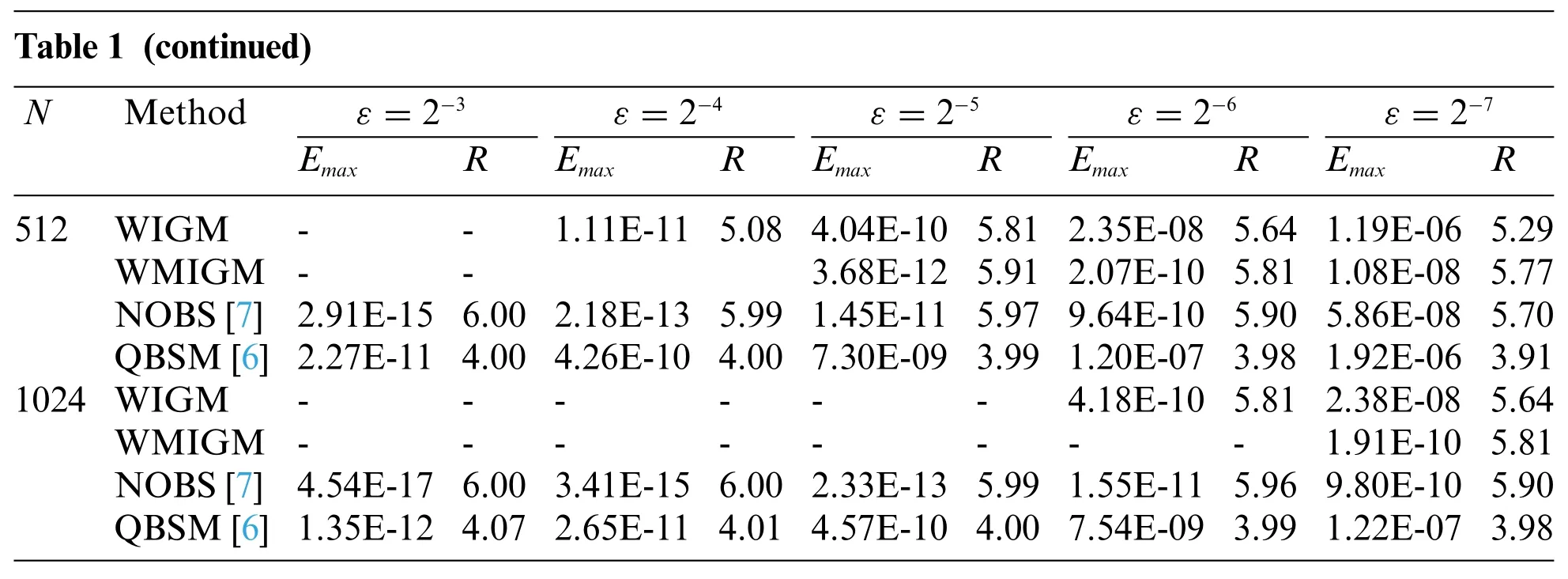
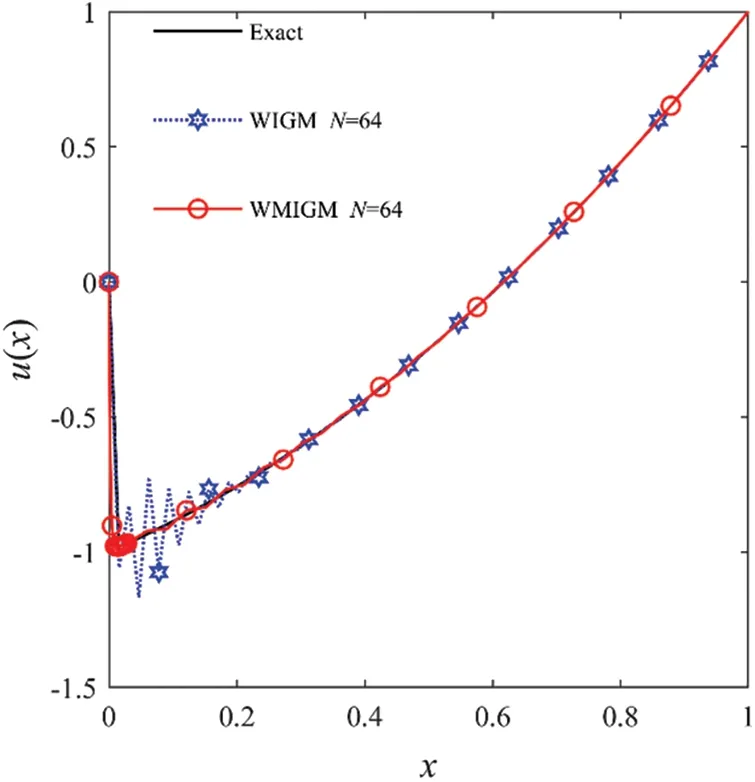
Figure 2:The comparison of the numerical solutions with the exact solution for Example 1 with ε=2-9

Table 2 shows the comparison of the maximum absolute errors between the QBSM with Shishkin mesh[6],the NOBS with Shishkin mesh[7],and the proposed WIGM and WMIGM with respect to the number of grid points for various values ofε.It can be seen that the number of grid points must be increased to obtain a reliable numerical solution asεdecreases.We can see from Fig.4 that the method of locally enhancing nodes at the boundary layer using the WMIGM performs significantly better than the method utilizing uniform nodes using the WIGM when the same number of nodes is used.The latter has obvious spurious oscillations in the boundary layer region.The error norms as a function of the number of nodes are illustrated in Fig.5,whereε=2-7.We have shown that the WMIGM is much more accurate than the QBSM[6]and the NOBS[7],and the order of accuracy of the WMIGM withε-uniform error norm is approximatelyγ-1.Additionally,the maximum absolute error convergence rate of the WMIGM withγ=6 is approximately 6.18,which is larger than that of other algorithms.

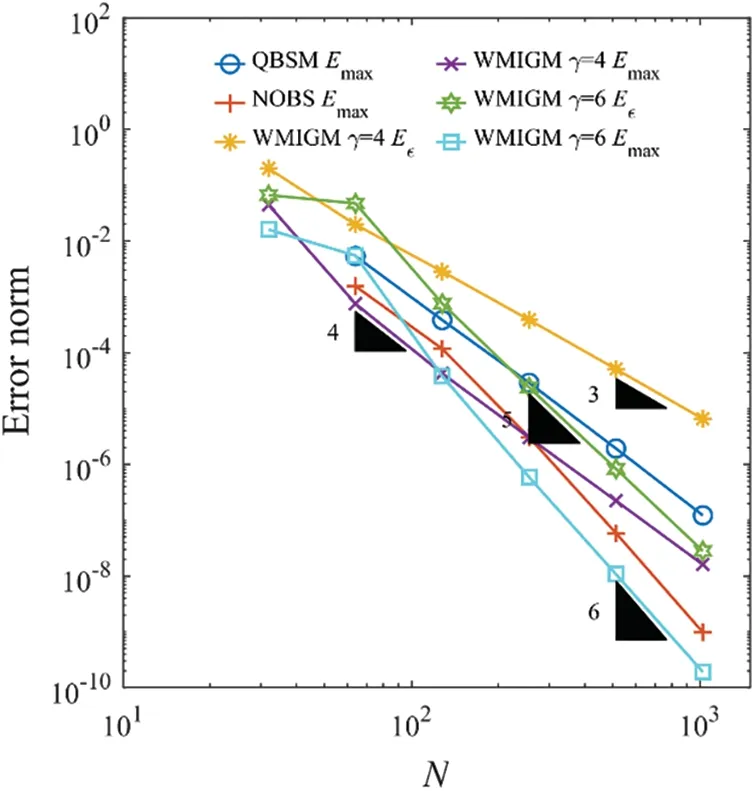
Figure 3:Error norm as a function of the number of grid points for Example 1 with ε=2-7

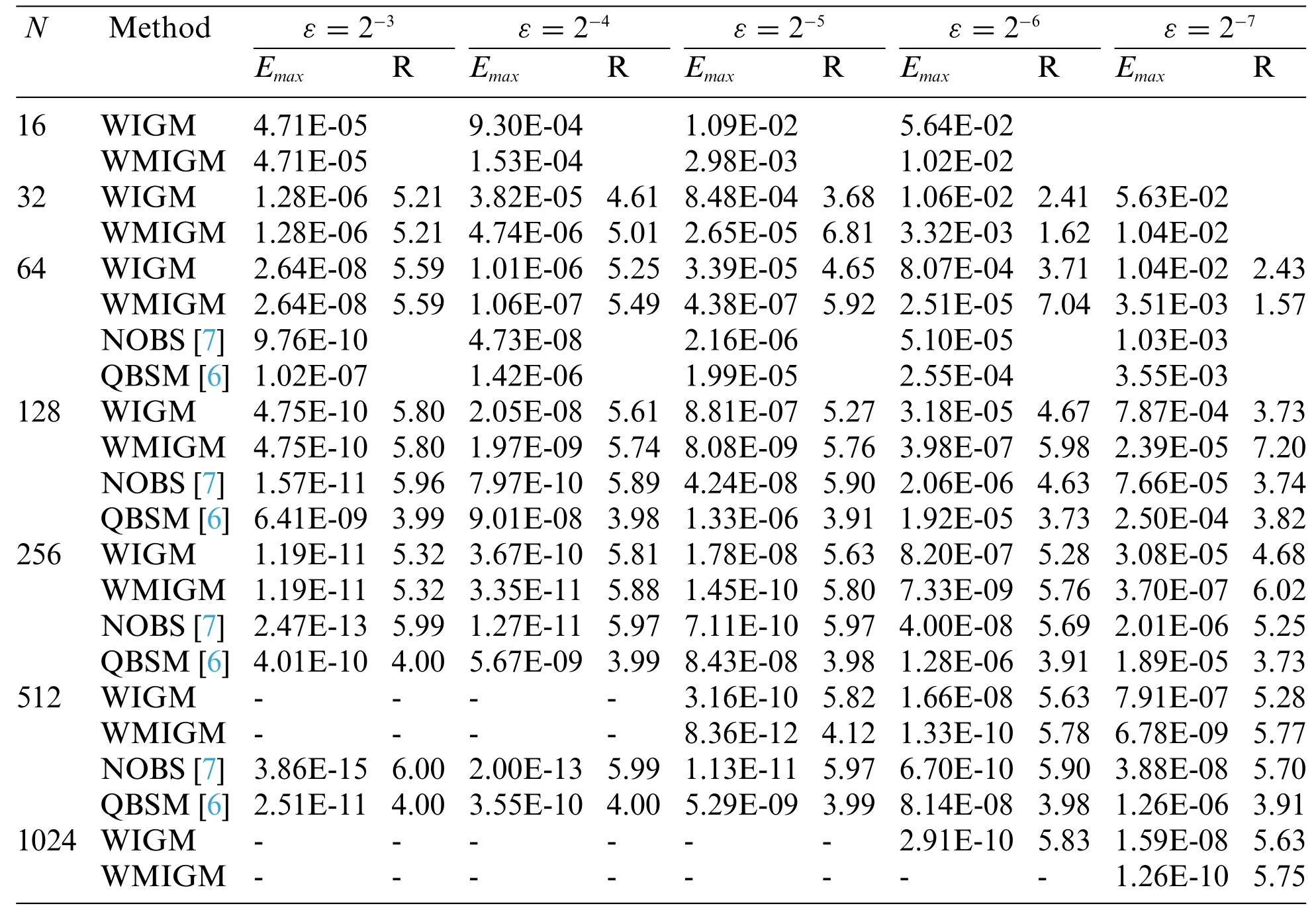
Table 2:Maximum absolute errors and convergence rate of Example 2 for different values of ε and N

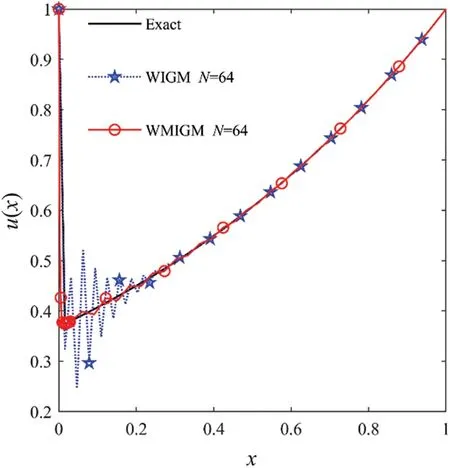
Figure 4:The comparison of the numerical solutions with the exact solution for Example 2 with ε=2-9

Figure 5:Error norm as a function of the number of grid points for Example 2 with ε=2-7

5.3 Test Problem 3:Right-Side Boundary Layer Problem

We next consider the right-side boundary layer problem[6,13,63-65]:

with boundary conditions ofu(0)=1 andu(1)=0.The exact solution of this problem is

Fig.6 displays the absolute errors for the uniform mesh with different values ofε,and we observe that the errors are mainly located in the right-side boundary layer region.The obtained maximum absolute errors and computational orders of convergence are presented in comparison with the existing QBSM method[6]in Table 3 for different values ofεandN.From this table,we can conclude that our numerical solutions obtained by the WMIGM are in good agreement with the exact values and are more accurate than the QBSM,which is a fourth-order scheme[6].It can also be seen from Fig.7 that the non-physical oscillation can be greatly reduced by locally increasing the number of nodes in the boundary layer.

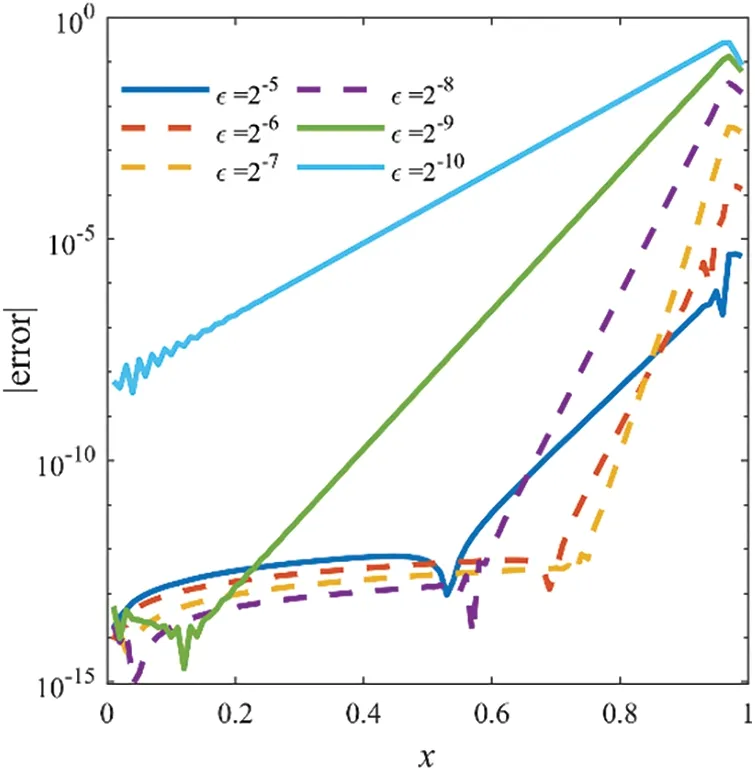
Figure 6:Absolute errors of WIGM for Example 3 with N=100

Table 3:Maximum absolute errors and convergence rate of Example 3 for different values of ε and N

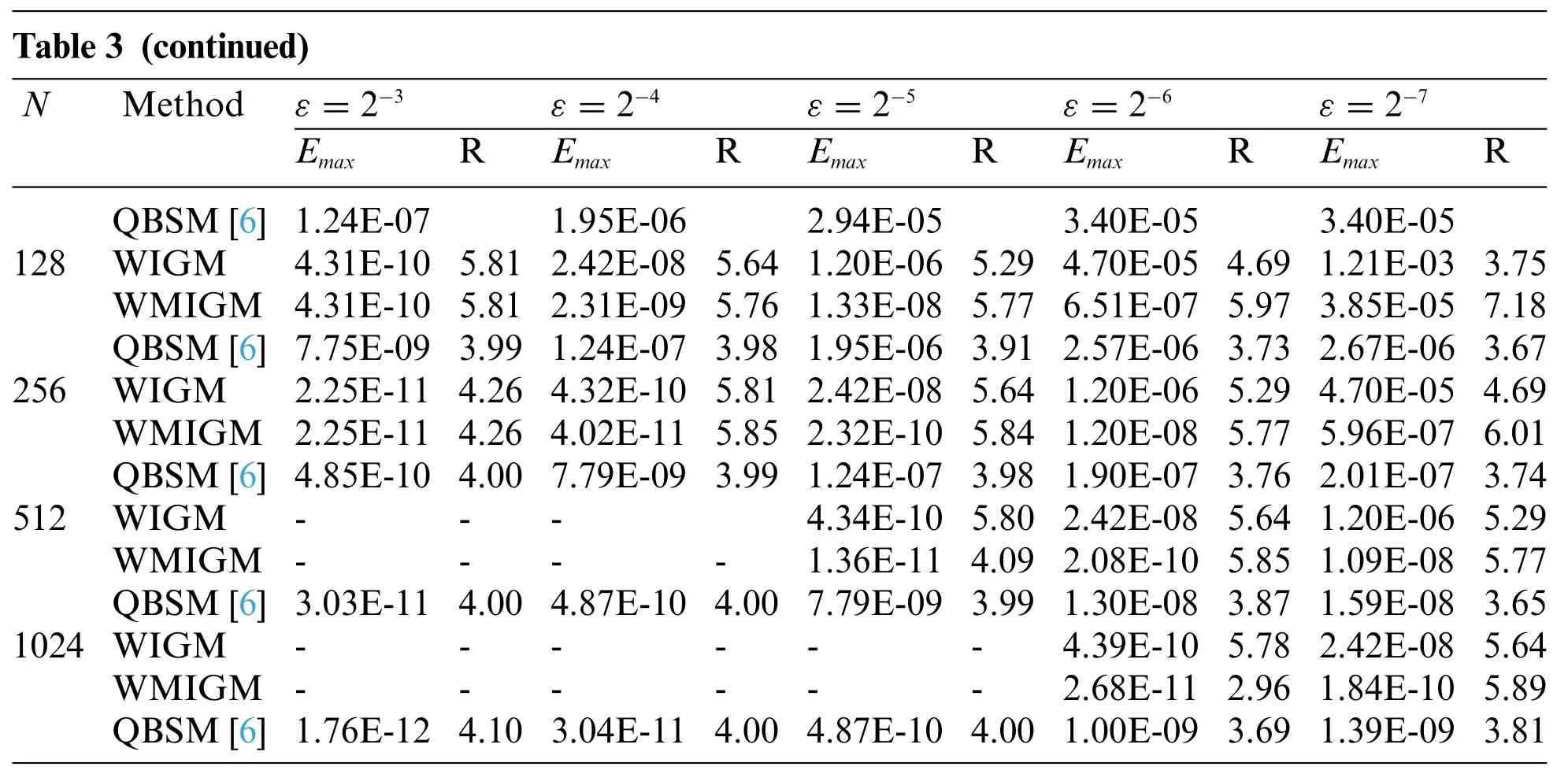
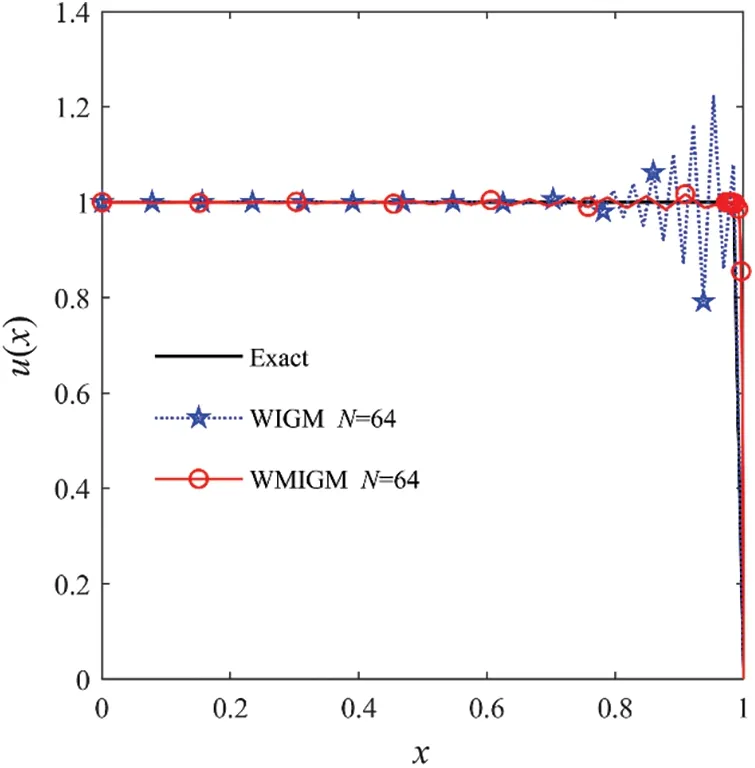
Figure 7:The comparison of the numerical solutions with the exact solution for Example 3 with ε=2-9

5.4 Test Problem 4:Right-Side Boundary Layer Problem

Finally,we consider the following homogeneous linear singularly perturbed boundary value problem[5,7,63,66,67]:

with boundary conditions extracted from the exact solution as

The maximum absolute errors obtained by the QBSM with Shishkin mesh [6],the NOBS with Shishkin mesh [7],and the proposed WIGM and WMIGM are presented in Table 4.It is evident from this table that WMIGM can achieve more accurate approximate solutions.A comparison of the numerical and analytic solutions withε=2-9is shown in Fig.8.The accuracy of the present wavelet solution near the right-side boundary layer was improved with the addition of local nodes.Fig.9 shows that the convergence rate of the proposed WMIGM withγ=6 is 6.19,whereas the convergence orders of the QBSM with Shishkin mesh [6] and the NOBS with Shishkin mesh[7] are only 3.81 and 4.89,respectively.Therefore,the WMIGM is significantly more accurate than these previously developed methods.

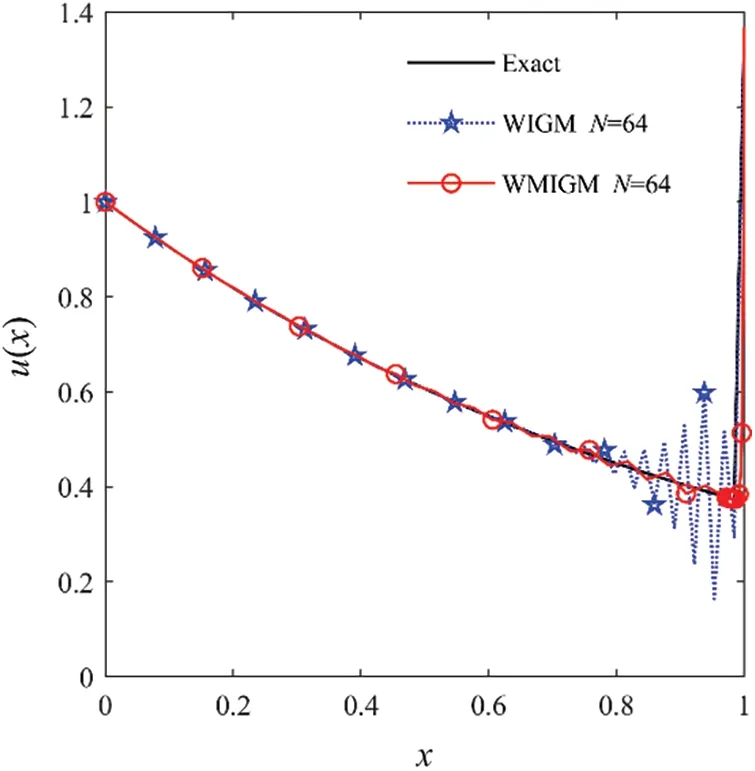
Figure 8:The comparison of the numerical solutions with the exact solution for Example 4 with ε=2-9

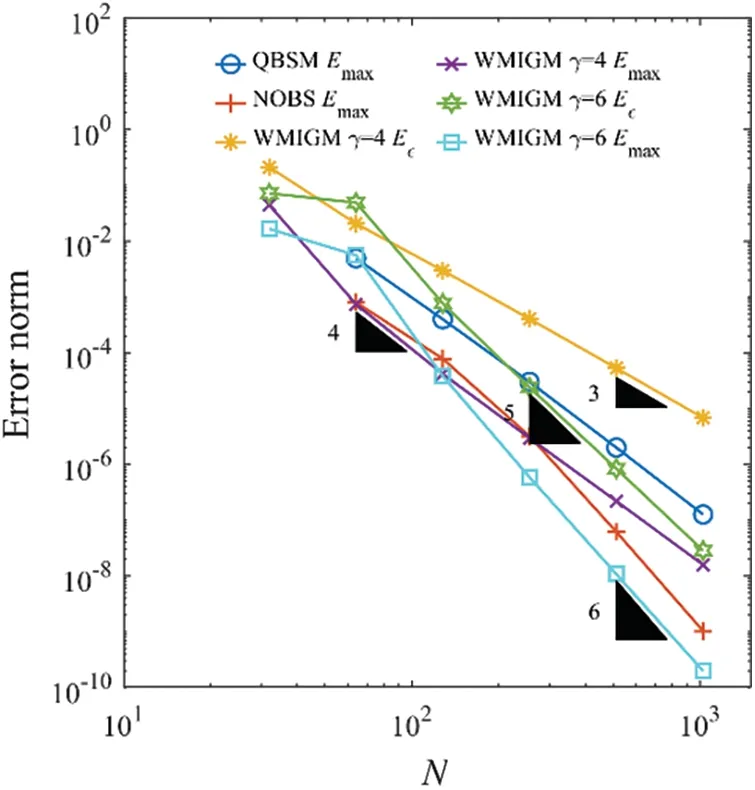
Figure 9:Error norm as a function of the number of grid points for Example 4 with ε=2-7

6 Conclusion

In this study,we extended the WMIGM to solve linear singularly perturbed boundary value problems with modified Shishkin nodes.The proposed wavelet scheme was verified by comparing the numerical solutions obtained via the QBSM with Shishkin mesh and the NOBS with Shishkin mesh.The numerical results confirm the theoretical analysis and demonstrate that WMIGM has several advantages over existing schemes:

(1) The accuracy of the WMIGM is significantly better than that of the WIGM.The approximate solutions obtained by the WMIGM exhibit no obvious spurious oscillations near the boundary layer,even as the perturbation parameter approaches zero.

(2) The WMIGM exhibits greater accuracy than existing schemes,including those of the QBSM and NOBS methods with Shishkin mesh.

(3) The WMIGM demonstrates a six-order convergence rate and retains a stable convergence order better than that of the QBSM and NOBS methods with the Shishkin mesh.

These advantages indicate the potentially wide application of the WMIGM to simulating problems with local large gradients.Since the proposed WMIGM allows a very flexible nodal distribution,it can be extended to solve other problems with localized steep gradients,such as the steady-state convection diffusion problems,the steady-state heat transfer at high Pe´clet numbers,and the planar thin plate problems in solid mechanics.Additionally,the combination of the time integral format and the proposed method enables the solution of time dependent systems,including the Navier-Stokes equations with large Reynolds numbers and convective heat transfer problems with large Péclet numbers.Moreover,combining WMIGM with wavelet adaptive analysis holds great appeal as a potentially superior method for solving these intricate problems.

Acknowledgement:The authors sincerely thanks the reviewers and the editors of the journal for the great improvement of this paper.

Funding Statement:This work was supported by the National Natural Science Foundation of China(No.12172154),the 111 Project(No.B14044),the Natural Science Foundation of Gansu Province(No.23JRRA1035),and the Natural Science Foundation of Anhui University of Finance and Economics(No.ACKYC20043).

Author Contributions:The authors confirm contribution to the paper as follows:study conception and design:Jiaqun Wang,Xiaojing Liu;coding:Jiaqun Wang,Guanxu Pan;analysis and interpretation of results: Guanxu Pan,Xiaojing Liu;funding support: Jiaqun Wang,Youhe Zhou,Xiaojing Liu;draft manuscript preparation:Jiaqun Wang,Guanxu Pan;draft review: Youhe Zhou,Xiaojing Liu.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.