An Overview of Sequential Approximation in Topology Optimization of Continuum Structure

Kai Long ,Ayesha Saeed ,Jinhua Zhang ,Yara Diaeldin ,Feiyu Lu ,Tao Tao ,Yuhua Li,★,Pengwen Sun and Jinshun Yan

1State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources,North China Electric Power University,Beijing,102206,China

2Faculty of Materials and Manufacturing,Beijing University of Technology,Beijing,100124,China

3New Energy and Energy Storage Division,China Southern Power Grid Technology Co.,Ltd.,Guangzhou,510080,China

4School of Mechanical Engineering,Inner Mongolia University of Technology,Hohhot,010051,China

5College of Energy and Power Engineering,Inner Mongolia University of Technology,Hohhot,010051,China

ABSTRACT This paper offers an extensive overview of the utilization of sequential approximate optimization approaches in the context of numerically simulated large-scale continuum structures.These structures,commonly encountered in engineering applications,often involve complex objective and constraint functions that cannot be readily expressed as explicit functions of the design variables.As a result,sequential approximation techniques have emerged as the preferred strategy for addressing a wide array of topology optimization challenges.Over the past several decades,topology optimization methods have been advanced remarkably and successfully applied to solve engineering problems incorporating diverse physical backgrounds.In comparison to the large-scale equation solution,sensitivity analysis,graphics post-processing,etc.,the progress of the sequential approximation functions and their corresponding optimizers make sluggish progress.Researchers,particularly novices,pay special attention to their difficulties with a particular problem.Thus,this paper provides an overview of sequential approximation functions,related literature on topology optimization methods,and their applications.Starting from optimality criteria and sequential linear programming,the other sequential approximate optimizations are introduced by employing Taylor expansion and intervening variables.In addition,recent advancements have led to the emergence of approaches such as Augmented Lagrange,sequential approximate integer,and non-gradient approximation are also introduced.By highlighting real-world applications and case studies,the paper not only demonstrates the practical relevance of these methods but also underscores the need for continued exploration in this area.Furthermore,to provide a comprehensive overview,this paper offers several novel developments that aim to illuminate potential directions for future research.

KEYWORDS Topology optimization;sequential approximate optimization;convex linearization;method of moving asymptotes;sequential quadratic programming

Nomenclature

g0Objective function

gjConstraint functions

xThe design variable vector containing the componentxi

KThe global stiffness matrix

FExternal load vector

UNodal displacement vector

EiTheith elemental young’s modulus

E0Young’s modulus of solid material

EminThe minimum stiffness with typical value ofE0/109

λLagrangian multiplier

||·||2Euclidean norm

u,vPenalization factor

VTotal volume in the structural design domain

cStatic compliance

fEInterpolation for young’s modulus

fvInterpolation for volume fractiontiThe ith independent topological variable

xi,Maximum and minimum design variable

ui,liLower and upper bound for moving asymptotes

αi,βi,γParameters in MMA algorithm

HHessian matrix

AHessian matrix in Lagrangian function

1 Introduction

In a seminal work published in 1988,Bendsøe et al.introduced the homogenization theory into structural design and proposed the so-called homogenization methodology for topology optimization of continuum structures[1].Since then,numerous approaches have emerged including variable density methods[2,3],evolutionary structural optimization method[4]and its improved version-bidirectional evolutionary structural optimization method(BESO)[5],a level-set method[6,7],moving morphable components framework [8],a feature-driven method [9].The latest review or monograph on a particular topology optimization approach can be found in the literature for the density-based method[10],for BESO method [11],for level-set method [12],for feature-driven method [13],the floating projection method and its extension [14-16].The above-mentioned numerical methodologies tend to permeate each other,which sometimes distinguishes their differences strictly [17,18].Nowadays,with the implementation of topology optimization functions in popular commercial software,such as ANSYS,MSC Nastran,Abaqus,Hyperworks,TOSCA Structure,and so on,topology optimization has achieved widespread success in a variety of engineering applications,particularly in the aircraft and aerospace industry [19-21],building [22],additive manufacturing [23,24],meta-material and concurrent design[25,26]and energy industry[27-29],where weight,cost,and environment are strictly limited.

A multitude of design variable update schemes are now available in the topology optimization community[17].Thanks to the educational paper and its open-source codes in all types of methods or one aspect of a specific problem,the beginners started their research without the need to grasp the sequential approximation concept and instead focused on the difficulties of a particular problem[30,31].The rapid growth of topology optimization is largely attributable to the solid theoretical foundations established by the pioneers’researchers in this area.In contrast to other critical technologies such as sensitivity analysis,filtering techniques,post-processing,etc.,the development of sequential approximations and their corresponding optimizers has been relatively slow.The motive of this article is to review the utilization of the sequential approximation in structural optimization studies,especially in topology optimization.Several novel progresses are presented,to irradiate further research.

2 General Mathematical Formulations for Topology Optimization

Let us consider the general topology optimization problem with an objective function g0total number of J constraint functionsgj:

wherexis the design variable vector containing the componentxi,with the lower and upper boundand

Assuming linear elasticity for continua,the equilibrium equation can be stated asKU=F.HereKrepresents the global stiffness matrix andFis the external load vector.Solving the equilibrium equation yields a nodal displacement vectorU.It is virtually impossible to articulate the vectorUas an explicit formula with design variables for complex engineering problems.However,the equilibrium equations forUcan be solved numerically for any set of design variables.

By writing the displacements as functions of the design variables via solving equilibrium equations,we acquire the nested formulation of the optimization problem as follows:

In the following section,we will introduce the most popular optimization solvers in topology optimization,such as optimality criteria(OC),sequential linear programming(SLP),convex linearization(CONLIN),method of moving asymptotes (MMA),sequential quadratic programming (SQP),and others.Topology optimization of continuum structure process explained through a flowchart as shown in Fig.1,via different steps:

Step 1:Define the design area for optimization

Step 2:Determine the design model-related parameters for topology optimization

Step 3:Implement the interpolation scheme for SIMP(Solid isotropic material with penalization)to predict material distribution within space.

Step 4: Perform sequential approximation (OC,SLP,CONLIN,SQP,MMA) for continuum structure optimization.

Step 5:Determine whether the convergence condition is satisfied,if satisfied then stop the iteration otherwise return to Step 4.

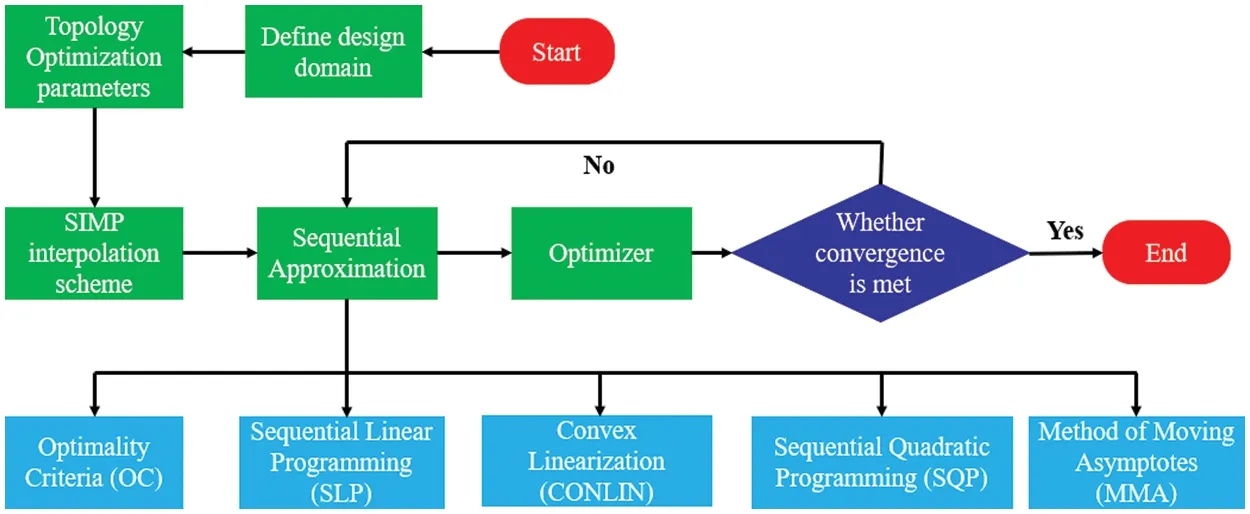
Figure 1:Flowchart for topology optimization of continuum structure using sequential approximation

2.1 Optimality Criteria

The variable density method,especially with the solid isotropic material with penalization(SIMP)interpolation,is undoubtedly one of the most renowned approaches due to its simple concept.The penalization scheme assumes a relationship between the elemental Young’s modulusEiwith the relative densityρi,i.e.,Ei=Here(p≥1)is the exponent power andE0refers to Young’s modulus of solid material.Applications of thousands of variables typically present optimization solution challenges.Formulated as follows is a heuristic design variable update scheme,also known as optimality criteria.

where both the move-limitmand damping parameterηare employed to stabilize the optimization loop.The lower boundis used to ensure the non-singularity in the finite element analysis.

The termBiin Eq.(3)can be defined as follows:

where the static compliance c and structural design volumeVare adopted as the objective and constraint functions for the static optimization problem.The symbolλdenotes the Lagrangian multiplier that can be attained by a bi-sectioning strategy to meet the predefined volume constraint.Due to the prevalence of the 99-line educational program [33],newcomers are more attracted to topology optimization research with the foregoing formulation.

In the density-filter approach [34,35],a modified SIMP interpolation scheme is expressed as follows:

whereEminhas a similar function to the parameterwith the typical value ofE0/109.Thus,ρiis employed in the finite element analysis,which serves as physical density.And it can be zero in the density-filter interpolation scheme[36,37].

In the presented OC algorithm,the Lagrange multiplier associated with a constraint is typically obtained via bisection search.Kumar and Suresh proposed a direct manner for the Lagrange multiplier,which exhibits several benefits including,fewer iterations,robust convergence,and insensitivity to the given material and load[38].

The intuition-based OC scheme permits efficient solutions of the computationally demanding problems in a relatively low number of iterations,especially for the compliance minimization issue with a single volume restriction.As all gradients have negative indicators,removing material will always increase compliance.However,conservative variable update by adjusting parameters allows the OC scheme to be applied to the flexible mechanism design and material design issues with material usage limits[39-41].In addition,Amir proposed a compliance-contained OC technique employing a similar bisection strategy to resolve the volume minimization issue[42].For instance,the optimized 2D and 3D cantilever structure obtained from the compliance-contained OC algorithm that is displayed in Fig.2.Groenwold et al.demonstrated the consistency of the OC and the sequential optimization based on exponential intermediate variables[43,44].In the following sections,the approximate function based on intermediate variables will be described.

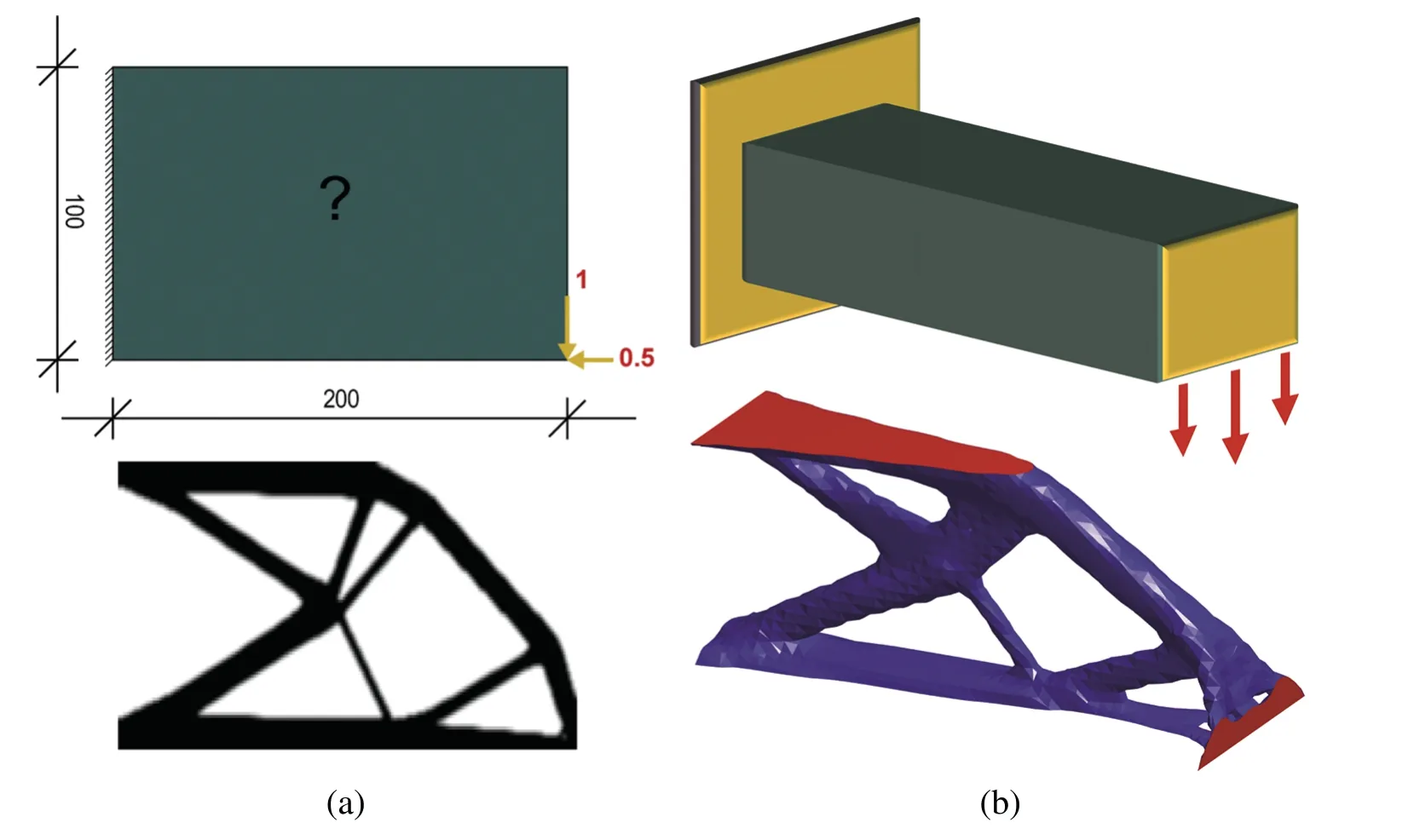
Figure 2: The optimized results from compliance-contained OC algorithm for: (a) 2D cantilever structure;(b)3D cantilever structure

2.2 Sequential Linear Programming

For optimization problem(1),the objective function and all constraints can be linear at the designx(k),resulting in the SLP sub-problem during thekthiteration:

Eq.(6) is an explicit approximation of the original problem (1) after obtainingg0,gjand all gradients for objective and constraint functions,which can be efficiently solved by mature algorithms in linear programming.As the linear Taylor expansion approximates locally,it is strongly advised to integrate a move limit into the actual optimization solution.

At present,solving topology optimization problems with SLP is uncommon.It is not surprising because the accuracy of this approximation is inferior to those that will follow in this paper.In the composite optimization problem,manufacturing constraints take the form of linear constraints,which makes the SLP algorithm more efficient at finding a solution[45,46].

2.3 Convex Linearization

Even for seasoned researchers,sequential structural approximation using reciprocal variables can be somewhat confounding.This is demonstrated by introducing an intervening variabley(x)for the sake of simplicity.The following expression can be derived from the linear Taylor series expansion:

The partial derivative ofgwith regard to the intervening variableyican be calculated using the chain rule:

When we choose the equationsyi=xioryi=1/xi,Eq.(7)can be reformulated as follows:

The Eq.(9) is indeed the linear Taylor expansion,whereas the Eq.(10) is called the reciprocal Taylor expansion.To distinguish between two equations,the superscriptsLandRare adopted.

Fleury defined the approximation ofgatx(k)by the combination ofgLandgRin COLIN[47-49]:

In Eq.(11),the sets are defined as follows:

The COLIN is also known as a conservative approximation [50],i.e.,for every possible setsS+andS-,the following inequality is true:

Thus,the sub-problem using CONLIN approximation can be reformulated:

Based on inequality Eq.(13),it can be inferred that the solution of Eq.(14) must be more conservative,i.e.,the objective function is larger than that of Eq.(1).

The CONLIN was furthered by multiple researchers.For example,Zhang et al.proposed a modified CONLIN approximation,which strengthens the convexity of the problem by introducing a convex factor[51].In engineering software,the CONLIN approximation was successfully implemented in the early version of OptiStructTM,even as a milestone of topology optimization in this code [52].Fig.3 plots the optimized jacket structure of offshore wind turbine done by the authors’group using OptiStructTM.

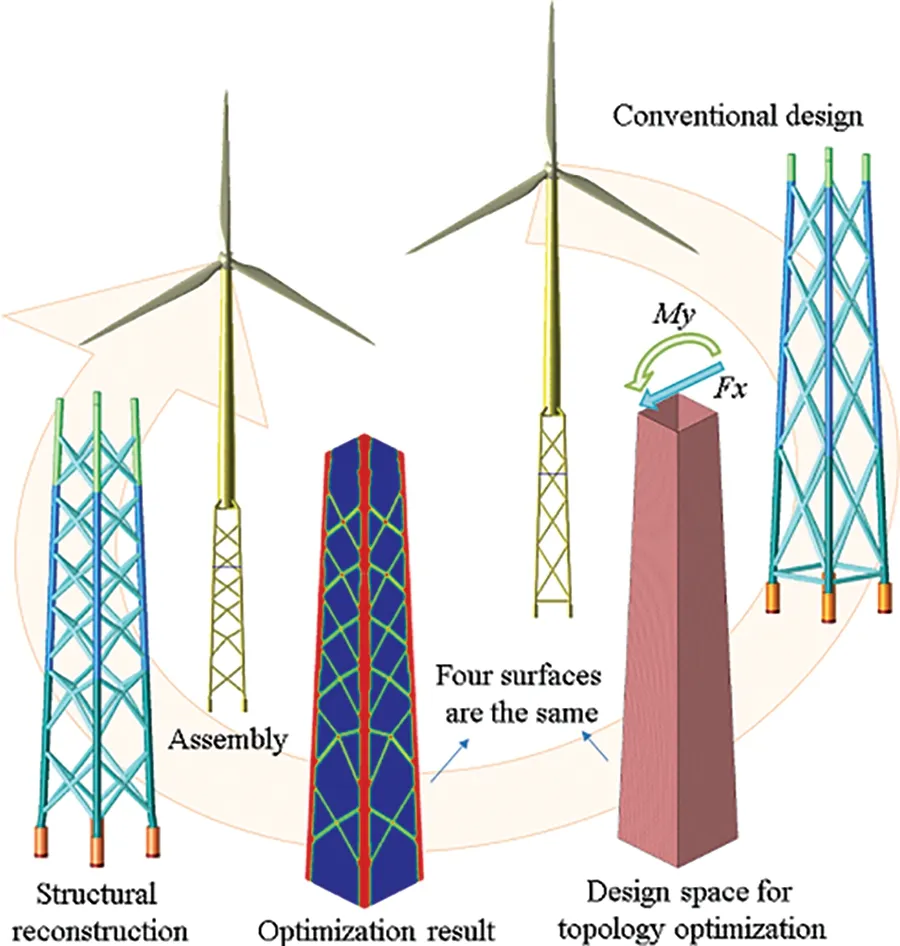
Figure 3:Optimization design procedure of jacket structure for offshore wind turbine

Example I Weconsider a fourth-order functiong(x)=and evaluate the CONLIN approximation atx1=1 andx2=6.

By differentiatingg,we obtain thatThe CONLIN approximation is the linear and reciprocal approximation atx1andx2,respectively.For comparison,we also depict all curves representinggC,gL,andgRin Fig.4.We can observe that thegCis always greater than or equal togLandgR,which is the reason that the CONLIN approximation is also named as a conservative approximation.

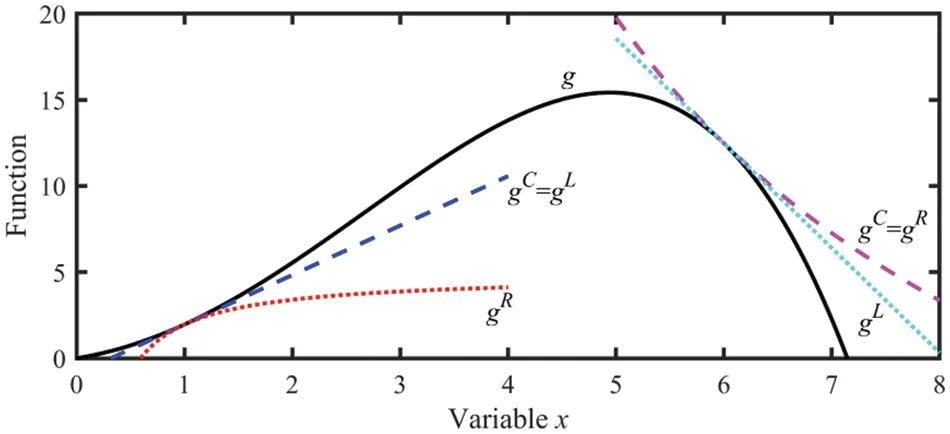
Figure 4:CONLIN approximation of the function g

2.4 The Method of Moving Asymptotes

Despite the fact that COLIN has demonstrated its efficacy for a variety of structural optimization problems,it occasionally converges slowly due to excessively conservative approximations.In contrast,it does not converge at all,indicating that it is insufficiently conservative.To stabilize the optimization process,Svanberg developed a variant of COLIN by constructing artificial asymptotes [53].The intervening variables in MMA are specified as follows:

wherelianduiare the moving asymptotes.Throughout the whole optimization process,the following in equation will always be satisfied:

In MMA,the approximating function atx(k)can be expressed as follows:

Thus,the approximate structural optimization problem using MMA can be rewritten:

For the SIMP method,the MMA algorithm is widely regarded as one of the most dependable and efficient optimizers [17].Followed by MMA,Svanberg proposed a class of globally convergent versions of MMA(GCMMA),also taking into account the optimization efficiency[54].In GCMMA,the parametercorresponding Eqs.(18)and(19)can be concurrently nonzero,leading to the approximation’s non-monotonic behavior.

Example IIWe choose the same functiongas in Example 1,aiming to illustrate the MMA approximation.The upper asymptote is set as 1.5,4,20,and 104.Fig.5 plots the MMA approximations for various values of the upper asymptotes.

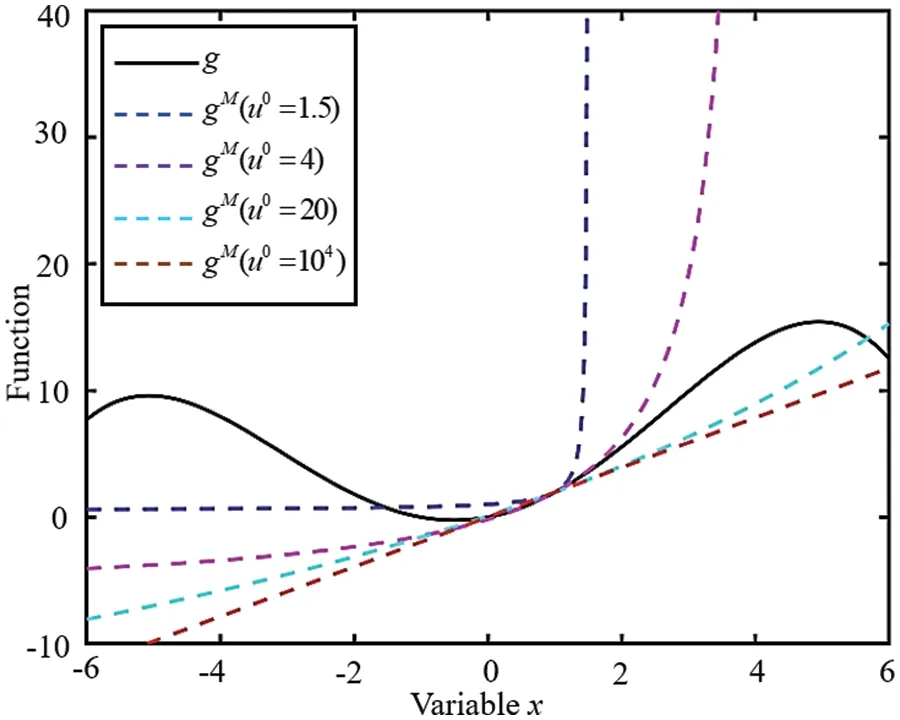
Figure 5:MMA approximation of the function g

We can see that as the upper asymptote approaches infinity from Fig.5,the MMA approximation is almost linear,which is in agreement with the SLP.

In addition,the MMA algorithm is also used as the optimizer in various topology optimization methods,such as the stiffness spreading method [55-57],parameterized level-set method [58],an approach driven by MMC and moving morphable bars[59-61],series-expansion framework[62-64],the iso-geometric based method [65].In addition to the compliance minimization problem,MMA is also applied to various non-self-adjoint problems,such as stress-constrained problems [66,67],fiber orientation optimization problems[68],transient excited and geometrically nonlinear structures[69,70],transient heat conduction[71],fail-safe design[72].Among them,the default parameters may be different,and some numerical skills and experience are required for some particular methodologies or problems.As far as the authors are aware,the sensitivity-based topology optimization solver in commercial software TOSCA StructureTMis the basis of the MMA algorithm.Fig.6 depicts an optimized mainframe in wind turbine by TOSCA StructureTM.

Figure 6:A optimized mainframe in wind turbine by TOSCA StructureTM

2.5 Two-Point or Three-Point Approximation

The preceding approximation function is characterized by the first order approximation and makes use of current data.On the basis of previous optimization iterations,it is anticipated that more precise approximations over a broader range can be attained.

Typically,Fadel et al.proposed a two-point approximation with the intervening variables[73]:

According to Eq.(7),we can obtain the following approximate function:

In Eq.(23),the undetermined parameterμiwill be achieved based on the gradient information from the previous iteration which yields:

It is not surprising that several two-point or three-point approximation functions were proposed to enhance approximate accuracy and expand the approximate range,the majority of which were numerically tested by mathematical problems and truss optimization problems[74-81].

2.6 Sequential Quadratic Programming

When the second-order term is appended in the Taylor expansion of the objective function in SLP,the following SQP-based approximation occurs:

where the Hessian matrixHcan be viewed as the only distinction between the SQP and the SLP.According to matrixH,structural optimization problems solved by SQP can be roughly classified into two groups,i.e.,SQP with approximate Hessian and exact Hessian.In comparison to the first-order approximation,topology optimization of continuum structure has not been a particularly fruitful domain for quadratic approximations.

2.6.1SQPwithApproximateHessian

One way to construct the SQP is the utilization of Newton’s method to find the stationary point of the Lagrangian function:

whereλjrepresents the Lagrangian multipliers associated with the constraintsgj(x).Take a secondorder Taylor expansion of the Lagrange function atx(k):

The complete Hessian matrixAof the Lagrangian function in the Lagrange-Newton method can be calculated through Eq.(28).

The computation and storage of Hessian matrixAare burdensome due to the large number of design variables in structural optimization problems.To utilize the second derivative information efficiently in structural optimization problems,Fleury developed the diagonal SQP method and introduced parametersδito control the move limit of design variables[82-84].

In certain practical situations,the second-order sensitivity information is undesirable.To overcome these difficulties,Grovenwold et al.proposed an incomplete series expansion(ISE)in which the approximate Hessian matrixis constructed using first-order gradient information in the current design point and objective function in historic design points[85-88]:

where the symbol ||·||2denotes the Euclidean norm.The convexity of ISE approximation can be enforced by restricting the diagonal termsto be zero or positive.In addition,the approximate Hessian matrix might contain even higher-order derivative information,deriving a family of approximation functions.

TopSQP is an efficient second-order SQP algorithm developed by Rojas-Labanda and Stople for structural topology optimization[89].The TopSQP optimization framework concludes with two phases:an inequality quadratic phase(IQP),in which an inequality-constrained convex quadratic subproblem is solved,and an equality-constrained quadratic phase(EQP),in which the active constraints found for the IQP are implemented.Both the IQP and EQP phases utilize the approximate Hessianof the Lagrangian function:

Rojas-Labanda and Stople conducted a comprehensive benchmark of topology optimization problems in conjunction with various optimizers,such as OC,MMA,and SQP.They concluded that the second-order information aids in obtaining accurate results and that SQP outperforms all other solutions for classical benchmark solvers[90].For issues involving Stokes flows,Evgrafov developed a method for minimizing dissipated power that converges locally[91,92].

Recently,Zhang et al.[93] and Yan et al.[94] applied the SQP with approximate Hessian in discrete material optimization.Referring to Powell’s work[95],the Hessian matrix is replaced by an approximate matrix

Generally,the SQP with approximate Hessian has garnered the interest of numerous academicians in structural optimization.No matter how the approximate methodology differs,one common pursuit is to obtain faster convergence at the lower calculation cost of sensitivity information.

2.6.2SQPwithExactHessian

Different from the aforementioned SQP family algorithms constructed second-order information based on mathematical programming,Sui et al.proposed a novel formulation,also known as the independent continuous mapping (ICM) method in 1996 [96],which can be viewed as an extension of the size optimization problem proposed [97-101].This method is regarded to achieve topology optimization through material distribution.The description of the first letter“I”in the ICM method represents the topological variable of theithelementtiis independent of the physical parameters such as section area,relative density,and so on.Also,Young’s modulus and elemental volume are independently defined:

wherefE(ti) andfv(ti) relate to Young’s modulus and volume of solid material with the topological variable,respectively.

A typical formulation for the function in Eq.(35)can be written as follows:

whereμandνare the penalization factor.

The design variablesxihave the form of the reciprocal function offE(ti),i.e.,

When Eq.(37)is substituted into Eq.(38),it yields:

The elemental volume can be rewritten as follows:

According to Eq.(40),the first and second order derivatives with respect toxican thus be calculated:

In contrast to prevalent density methods,the ICM method focuses on minimizing the total volume or weight while maintaining constraints on various structural responses.Taking the compliance constraint as an example,the topology optimization formulated can be mathematically stated as follows:

whereVandrepresent the total volume in the structural design domain and the upper limit of the static compliance,respectively.andare the minimum and maximum design variables.

The volume function and compliance function can therefore be expressed by first-order and second-order Taylor expansion series.The original topology optimization problem can be converted as a quadratic program with second-order information,which provides another distinguishing feature over the widely used first-order method.From Eq.(41),we can easily obtain the second derivatives in Eq.(40) are always greater than zero.It can be inferred that the Hessian is positive definite and separable,which brings much allowing for efficient solution of the computationally demanding problem in a reasonable number of iterations.

Since the ICM approach was proposed,its applications have undergone tremendous developments with the efforts of their groups,also propelling the industry forward at the breakneck speed[102].Up to now,the ICM method has been successfully applied to various constraints on structural response,including multiple nodal displacements,natural frequency,buckling,and so on [103-109].In recent years,Peng et al.conducted systematic research based on the independence of design variables,by introducing the step function into the material property modeling [110-112].Fig.7 plots a typical optimized structure obtained from the ICM approach.

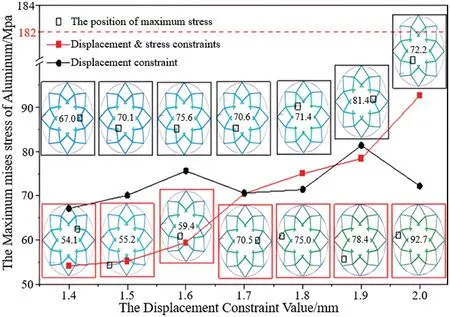
Figure 7:Optimized structures obtained from ICM approach

The ICM method aroused the attention of other scholars.Long et al.extended this method into the framework of meshless analysis [113],the stress-constrained problem for continuum structure subject to harmonic excitation [114],forced vibration structure containing multiple materials [115],transient heat transfer problem [116],concurrent design considering load carrying capabilities and thermal insulation[117],large-scale computing problem resort to reanalysis technique[118],fail-safe design combined with the load uncertainty [119],etc.[120].Rong et al.introduced a design space expansion strategy to stabilize the ICM optimization process[121-123].

2.7 Augmented Lagrange

In recent years,the AL method has emerged as a viable approach to topology optimization,especially for extensive constraints.The AL method addresses constraints directly by appending them to the objective function as a penalty term with variable parameters.AL is not a novel concept in the field of structural optimization.For instance,the parameterized level set method has been successfully implemented to enforce a sole volume constraint[124].

Utilizing three phase projections including eroded,intermediate,and dilated,da Silva et al.employed the AL function for stress-constrained topology optimization problems while accounting for manufacturing uncertainties[125],which was then extended to the robust design of the compliant mechanism subject to both strength design requirement and manufacturing uncertainty [126].For mass minimization under local stress constraints,Senhora et al.provided an AL-based topology optimization formulation by combining piecewise vanishing constraints [127].Later,Giraldo-Londono et al.generalized the AL technique for the transient topology optimization issue by including stress constraints at each time step[128].An aggregation-free local volume proportion formulation for porous structure was presented by Long et al.[129],which was subsequently developed into a multimaterial porous structure[130].The AL method is also performed to the topology optimization under constraints of multiple nodal displacements,maximum transient responses problem,and fatigueresistance issue [131-133].A porous bone structure using local volume constraint generated by the AL method is displayed in Fig.8.

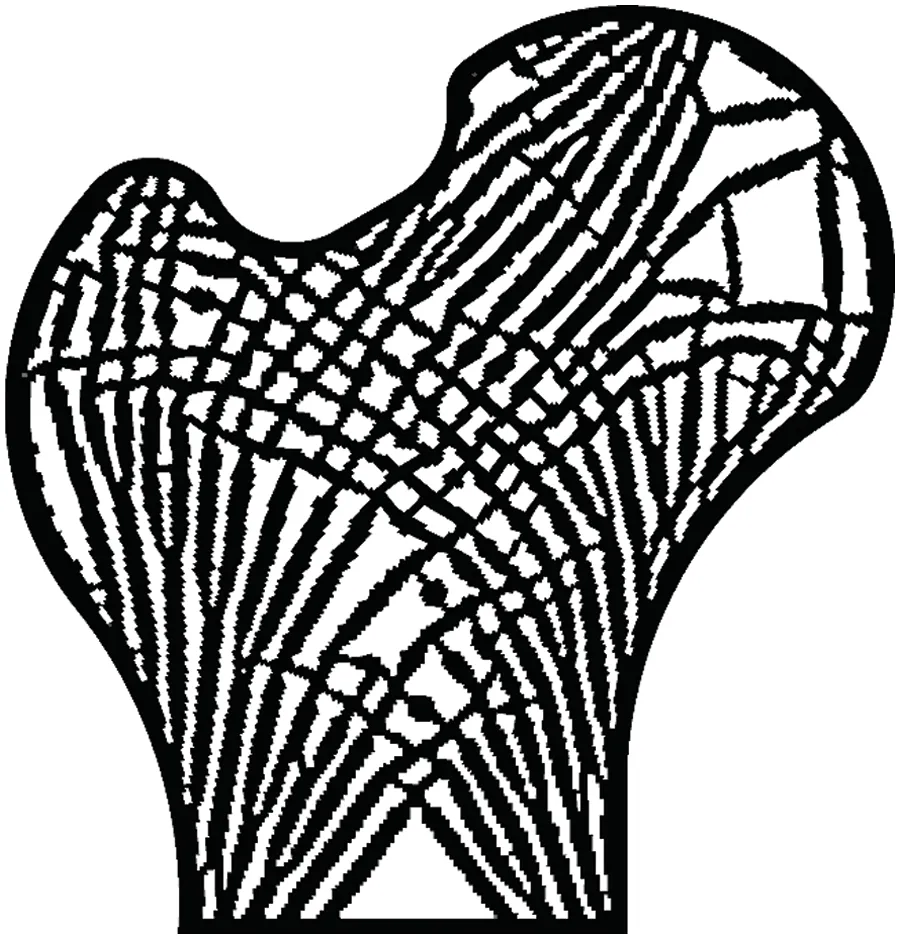
Figure 8:The porous structure generated by the AL method using local volume fraction

2.8 Sequential Approximate Integer Programming

BESO is the predominant discrete variable-based topology optimization approach.More recently,Sivapuram et al.treated topology optimization as a discrete variables-based optimized problem[134].In their formulation,the initial optimization problem is transformed into SLP,which is then solved by integer linear programming(ILP).They expanded binary structures method into continuum structures subject to fluid structure,fluid flow,and thermal expansion loads via such a fundamental innovation[135-137].And,they released the open-source code based on MatlabTMfor distribution[138].

Liang et al.suggested a sequential approximate integer programming with a trust region framework to restrict the range of discrete design variables by linearizing the non-linear trust region constraint [139].This provided method was also extended into 3D structures and convective heat transfer problems[140,141].

2.9 Non-Gradient Approximation

The majority of the existing topology optimization method is solved by the gradient-based algorithm,which is due in large part to the efficient sensitivity analysis approach.Sigmund gave a comprehensive analysis of the non-gradient topology optimization from multiple aspects including global solution,discrete designs,simple implementation,and efficiency,particularly for the SIMP method[142].

The two-point or three-point approximation belongs to the mid-range approximation.Since topology optimization requires repeated iterations until convergence,it is a natural choice to construct approximation functions using multi-point information to expand its approximate range.The approximation of this type can also be regarded as the connection of many local approximations,such as response surface and kriging model.Wang et al.presented a Hermite interpolation function using multi-point data generated during the iterative process of optimization[143].Huang et al.proposed a multi-point approximation by utilizing both the value of an implicit function and its derivatives [144,145].Although the multi-point approximation technique has been used in truss optimization,to the authors’best knowledge,the multi-point approximation has not been performed in the topology optimization of continuum structures.

Luo et al.described structural topologies using the material-field series expansion,with the series expansion coefficients serving as the design variables [62].This method has the added benefit of producing topologies with smooth boundaries.As a significant reduction of design variables,the structural approximation can be constructed on sensitivity or non-gradient data,such as Kriging models[146].As sensitivity derivation is avoided,the non-gradient approach with few design variables is now effectively applied to large deformation problems,micro-structural design,etc.[147-151].

Recent years have witnessed rapid progress in artificial intelligence and neural networks.Some researchers have focused on topology optimization using these techniques,in an effort to accelerate the optimization iterations or enhance graphics post-processing.AI technology is used to establish the implicit connection between structural response and design variables.Woldseth et al.performed a comprehensive analysis of the combination of artificial neural networks and topology optimization[152].Consequently,these associated studies fall outside the scope of this article.

2.10 Future Study

Authors are aware that the number of applicable optimizers is relatively limited,particularly for a wide range of multiphysics topology optimization with nontrivial and multiple constraints.For decades,the MMA and its globally convergent variant have been regarded as the most reliable optimizers.The authors conclude that inadequate research has been conducted on the use of contemporary mathematical programming techniques to solve large-scale,complex topology optimization problems.The AL method,ILP,and optimization algorithm based on non-gradient approximation require further development.

3 Conclusion

Sequential approximation,a crucial technique in topology optimization,has attracted a great deal of interest since the beginning of structural optimization.After decades of research advancements in topology optimization,the community has settled on a handful of sequential approximations.MMA and its global convergent version become dominant among them.This allows researchers to concentrate on other essential technologies.This paper provides a comprehensive overview of sequential approximation,its related topology optimization methods,and its applications.The initial section provides a concise introduction to the optimality criteria and sequential linear programming.The subsequent section introduces the intervening variables in order to explore various forms of sequential approximation,including COLIN,MMA,two-point or three-point approximation,and SQP.This paper presents the latest improvements in the field,including AL function,sequential approximate integer programming,and non-gradient approximation,aiming to aid researchers effectively choosing the most suitable approximate form for their studies.It is anticipated that a forthcoming proposal will present a notable advancement in the field of topology optimization,specifically in relation to sequential approximation.

Acknowledgement:We thank Professor Yunkang Sui(Beijing University of Technology)partly for his pioneering research on topology optimization solved by SQP since 1996,and partly for his personality on the first author’s scientific career.

Funding Statement:This work was financially supported by the National Key R&D Program(2022YFB4201302),Guang Dong Basic and Applied Basic Research Foundation(2022A1515240057),and the Huaneng Technology Funds(HNKJ20-H88).

Author Contributions:The authors confirm their contribution to the paper as follows:study concept,writing,and interpretation of results:Kai Long,Ayesha Saeed;data collection:Jinhua Zhang,Yara Diaeldin,and Feiyu Lu;analysis and design: Tao Tao,Yuhua Li;draft manuscript preparation:Pengwen Sun,Jinshun Yan.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:Data will be provided on request.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.