基于伴随方程和自动微分的雷达散射截面表面灵敏度计算

周琳，陈宪，黄江涛，*，邓俊，高正红

1.中国空气动力研究与发展中心，绵阳 621000

2.西北工业大学 航空学院，西安 710072

雷达隐身技术是提高目标生存能力的技术，低可探测特征是未来军用飞机应具备的重要特征之一［1-2］。随着反隐身技术的发展，飞行器的气动/隐身设计受到越来越多重视。基于伴随方程的雷达散射截面（RCS）梯度求解可以通过一次控制方程求解、一次伴随方程求解实现目标灵敏度的快速计算，是气动/隐身精细化设计的基础。

近年来，基于电磁场积分方程伴随方程的灵敏度计算方法及相应的梯度优化受到广泛关注［3-7］。基于伴随方程的电磁场优化早期主要应用在天线设计领域，Georgieva 等［8］在2002 年将伴随方程引入电磁场频域计算，研究了基于矩量法的伴随方程求解，并基于伴随方法对Yagi-Uda 天线进行了优化；Toivanen 等［9］将自动微分法引入基于矩量法的电磁场伴随方程的设计变量灵敏度求解中；Kataja 等［10-11］基于矩量法（MOM）［12］、多层快速多极子算法（MLFMA）［13-14］推导了电场积分方程的连续伴随表达式。

基于伴随方法的RCS 梯度计算在飞行器隐身优化问题中研究较晚，公开文献较少。Bondeson 等［15］推导了二维积分形式麦克斯韦方程的连续伴随方程，并对简单外形的RCS 进行了优化；周琳等［3-5］在MOM、MLFMA 的基础上推导了混合场积分方程的离散伴随方程，并对典型飞翼布局进行了气动隐身优化。Li 等［6］在MOM 的基础上提出一种基于伴随方程和自动微分的高效设计变量梯度求解方法，并对机翼进行了气动隐身优化。

虽然近年来基于伴随方程的气动隐身优化取得了较大进展，但尚无公开文献探讨RCS 的表面灵敏度求解方法。表面灵敏度可以反映表面网格位置的改变对目标函数的影响，一方面对优化设计有重要指导作用；另一方面设计变量的梯度可以根据表面灵敏度直接求出，从而克服经典基于伴随方程的设计变量RCS 梯度求解需反复填充阻抗矩阵的问题［3-4，8］，在经典伴随方程梯度求解的基础上进一步提升设计变量梯度的求解效率。飞行器气动优化领域伴随方法已较为成熟，已采用连续伴随方程［16］、自动微分方法［17］、网格伴随方程等方法［18-19］对目标的表面灵敏度的计算方法进行了深入研究，相对于气动问题，电磁场求解问题的阻抗矩阵是稠密矩阵，对于表面网格量庞大的复杂问题，计算和存储开销较大，且电磁场问题中的阻抗积分项与几何信息的依赖关系复杂，运算多为复数运算，难以手动推导得到。以上2 点都使电磁场问题的表面灵敏度求解更具挑战。

本文在矩量法的基础上提出基于自动微分的雷达散射截面表面灵敏度计算方法，以及适用于表面灵敏度存储的稀疏矩阵存储技术。该方法将基于自动微分法的阻抗矩阵偏导数求解嵌入阻抗矩阵并行填充循环中。对于任意数量设计变量和入射角度，将需进行一次阻抗矩阵、阻抗矩阵偏导数求解，从而使RCS 梯度计算时间与设计变量数无关；当入射角度改变时，计算所有设计变量梯度约为8 次矩阵乘，显著提升基于伴随的梯度求解效率。

1 基于伴随方程的RCS 梯度计算

典型雷达散射截面σ的减缩问题可表示为

式中：I为表面感应电流的基函数系数；D为设计变量向量；V-ZI=0 为离散形式的麦克斯韦方程组。

引入拉格朗日乘子Λ可以构造目标函数L

式（2）对设计变量D求导，有

令式（3）右端第1 项为0 即可得到伴随方程，又由

伴随方程可以表示为

求式（5）得到伴随变量Λ后，设计变量的RCS 梯度可以表示为

设计变量D的梯度也可以根据表面灵敏度间接求解。将式（6）中的D用r替换得到基于伴随方程的表面灵敏度计算方法

设计变量D与表面网格r的关系可以表示为

式中：Np为表面网格点数量；为RCS关于表面网格点rj=［x，y，z］在3 个坐标方向的灵敏度；为表面网格点rj与设计变量的关系，由网格变形算法决定。由于设计变量位置、入射角度的改变不影响∂Z/∂r的结果，因此梯度计算过程中只需要一次∂Z/∂r求解。而且基于表面灵敏度的设计变量梯度求解方法不需要反复填充阻抗矩阵Z，矩阵-矢量乘积Z的计算次数少，从而提升梯度求解计算效率。

2 RCS 表面灵敏度存储方法

采用表面灵敏度计算设计变量梯度的关键在于表面灵敏度的计算、存储及表面灵敏度与感应电流的矩阵-矢量乘。本节首先针对表面灵敏度存储量大的问题提出了表面灵敏度矩阵的稀疏存储技术。

式中：Ne为基函数个数。由于σ和V的求解表达式较为简洁，不涉及复杂的积分计算，因此∂σ/∂r、∂V/∂r可以通过自动微分直接求解，通过向量-向量相乘计算ΛT∂V/∂r，计算量较小。式（9）的难点在于∂Z/∂r的求解和的计算。理论上∂Z/∂r是维度为Ne×Ne×Np的大规模三维矩阵，无法直接存储，本节通过分析∂Z∂r的特点，提出一种点索引稀疏矩阵存储技术，将的计算量和存储量降到优化可承受的范围。

以电磁场积分方程求解最常使用的RWG（Rao-Wilton-Glisson）基函数［20］为例进行推导，RWG 基函数定义在一对相邻三角形的公共边上（见图1），第n条边对应的基函数fn(r)为

图1 基函数RWG 示意图［21］Fig.1 RWG basis function diagram［21］

由RWG 基函数的特点可知，每一阻抗矩阵元素Zmn至多只与8 个表面网格点的位置有关（图2）。因此，虽然∂Z/∂r理论上是维度为Ne×Ne×Np的大型三维矩阵，但∂Z/∂r中非零元素数量只有Ne×Ne×8，因此可以建立以网格点为索引的稀疏矩阵存储技术，从而显著降低∂Z/∂r的存储需求。

图2 Zmn存储示意图Fig.2 Zmn storage diagram

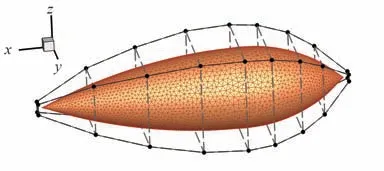
图3 双锥体外形及设计变量位置Fig.3 Design variables of double-ogive test case

在程序处理中，开辟整型索引数组Zdiff_index（Ne，Ne，8），并按图2 中Index 数组中点的记录顺序存储与阻抗元素Zmn有关的8 个网格点的全局编号。开辟复数数组Zdiff（Ne，Ne，8）存储Zmn关于每个相关网格点的导数∂Zmn/∂r。若与基函数m、n相关的4 个三角形间存在重合顶点，则与基函数Zmn相关的网格点数量将小于8，此时在索引数组Zdiff_index 和Zdiff 数组的相应位置补0。∂V/∂r的稀疏存储方法与此非常相似，不再赘述。

3 RCS 表面灵敏度计算方法

以电场积分方程为例详细分析表面灵敏度的计算技术。为将∂Z/∂x的计算嵌入阻抗矩阵Z的填充循环［22］，从而利用Z计算的中间结果，实现∂Z/∂r的高效求解，首先将Zmn的求解拆分成乘积项M1、M2和M2的组合，并将乘积项进一步拆分成积分项G 和H的组合。其中乘积项的表达式为

积分项G和H的表达式为

当场三角形与源三角形重合时积分项需采用奇异积分计算方法，不重合时可以采用高斯积分法。则的线性组合。

在阻抗矩阵Zmn填充循环的基础上采用自动微分法求解∂Z/∂r，采用Tapenade 自动微分工具［23］。自动微分方法通过分析程序源码，将复杂计算分解为简单运算的组合，根据链式求导法则得到复杂目标的梯度，自动微分法不产生截断误差，避免了差分法依赖步长的问题。∂Z/∂r的具体程序求解方法见算法1。其中最多与一条公共边相连的2 个三角形有关（6 个网格点），当考虑积分项在r=［x，y，z］3 个方向的导数时，分别为维度为1×3、3×3 的矩阵。

∂M1/∂r、∂M2/∂r、∂M3/∂r最多与一条公共边相连的2 个三角形有关（6 个网格点），根据链式求导法则，结合∂G/∂r、∂H/∂r的求解结果，可以得到

采用式（20）～式（22）结合算法1 可以得到∂Z/∂r在r=［x，y，z］3 个方向上的导数。由于实际优化中通常重点关注目标函数在z方向的梯度，因此程序实现时可以仅对z方向的梯度进行计算和存储，使向量-向量乘和矩阵-向量乘为标量乘，从而进一步降低计算量和存储量。同时，采用自动微分工具计算积分项和乘积项的偏导数时，需重复计算积分项和乘积项求解的中间量，可以通过修改自动微分得到的源码，降低重复计算量，从而进一步降低计算量。

完成∂Z/∂r的计算和存储后，需根据式（9）求解目标函数对网格位置的梯度dσ/dr，其核心是基于稀疏矩阵存储格式计算对于每个网格点ri，可以写为

从算法1 可以看到，提出的表面灵敏度计算方法中矩阵元素填充方法与矩量法基本一致，因此可以直接采用矩量法的并行策略［22］，较易实现并行求解，从而进一步提高计算效率。激励向量的自动微分梯度与阻抗矩阵的梯度计算非常类似，这里不再赘述。

4 表面灵敏度计算量分析

本节重点关注基于经典伴随方法和基于表面灵敏度方法求解设计变量梯度的计算量。工程问题中的隐身优化目标通常为给定角域的RCS 均值，记优化问题考虑的设计变量数为N，考虑的入射角度数为Na。2 种方法的计算量对比见表 1。

表1 设计变量梯度计算量对比Table 1 Gradient calculation amount comparison of design variables

梯度计算过程中需要扰动设计变量，生成新外形表面网格并计算新外形的阻抗矩阵Z(D+ΔD)，并进行矩阵-向量乘、向量-向量乘得到ΛTZ(D+ΔD)。由于每个入射角度的感应电流不同，因此计算N个设计变量在Na个入射角度的梯度需要进行N次表面网格变形计算、N次矩阵元素填充、N×Na次矩阵-矢量相乘运算、N×Na次矢量-矢量相乘运算。

对于基于表面灵敏度的梯度计算方法，表面灵敏度计算过程时需采用自动微分法计算∂Z/∂r，计算量大于阻抗矩阵填充，通过修改自动微分代码，复用阻抗矩阵填充的中间量可以提升∂Z/∂r的计算效率。由于∂Z/∂r与设计变量数量、入射角度无关，在梯度计算过程中仅需一次∂Z/∂r求解，因此虽然∂Z/∂r的计算量较大，但对梯度计算效率影响不大。∂Z/∂r所需的存储量约为阻抗矩阵存储量的8 倍。得到∂Z/∂r后计算该过程需要8Na次矩阵-向量相乘和8Na次向量-向量相乘运算。得到表面灵敏度后，根据式（8）计算设计变量梯度，计算时需依次扰动设计变量，由网格变形算法（如自由曲面造型法）进行表面网格变形计算得到dr/dD，与网格灵敏度dσ/dr相乘得到设计变量的梯度dσ/dD。在基于伴随方程的气动优化中，通常引入网格伴随方程［18-19］实现空间网格的dr/dD高效求解。由于基于麦克斯韦积分方程的RCS 求解仅需要对物体的表面进行网格划分，计算所需的网格量远小于气动求解，采用有限差分法计算dr/dD计算量较小。

5 算例验证

本节采用双锥体、球体、F22 外形和飞翼模型对提出的表面灵敏度计算方法进行验证，并探讨典型飞行器的表面敏感性特征。下文算例均以x-y平面为工作平面，计算RCS 在z方向的表面灵敏度。

1）双锥体模型

双椎体模型长0.190 5 m，由2 个锥角分别为22.62°、46.4°的半锥拼接而成（见图 3），是EMCC（Electromagnetic Code Consortium）［24-25］提供用于校验计算电磁学代码的标准算例之一。采用双锥体算例对采用的电磁场求解器和提出的表面灵敏度计算方法进行验证。双锥体算例计算采用的雷达波频率f=9 GHz，单站散射垂直极化（VV），定义沿x轴正向入射时入射角φ=0°，沿x轴负向入射时φ=180°。计算采用的网格平均尺寸约为λ/10，未知量总数N=11 094。

图4 为采用矩量法求解器的计算结果与实验结果［25］的对比，可见计算结果与实验结果吻合较好，证明采用的求解器具有较高精度，满足RCS评估和灵敏度计算的需求。

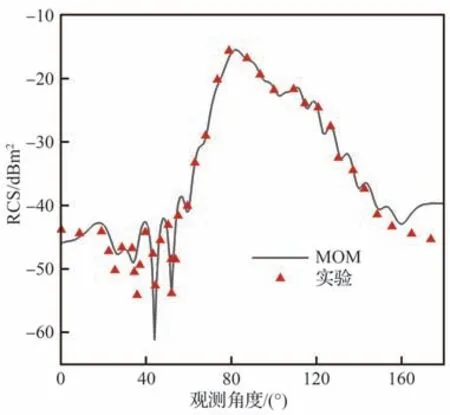
图4 双锥体外形RCS（f=9 GHz，VV 极化）Fig 4 RCS of double-ogive test case（f=9 GHz，VV）

采用域元法进行表面网格变形，采用表面灵敏度计算得到的设计变量梯度与有限差分计算结果对比见图5。可以看到，2 种梯度计算方法得到的结果具有良好的一致性，证明提出的表面灵敏度计算方法能够通过表面灵敏度的计算结果获取任意设计变量的梯度。

图5 表面灵敏度计算梯度与有限差分结果对比Fig.5 Comparisons of design variable gradient calculation by surface sensitivity and finite difference

图6 双锥体外形表面灵敏度（f=9 GHz，VV 极化）Fig.6 Surface sensitivity of double-ogive（f=9 GHz，VV）

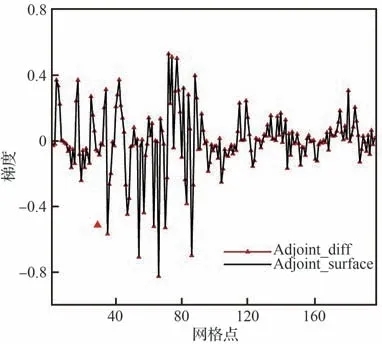
图7 表面网格点梯度对比Fig.7 Gradients of surface mesh

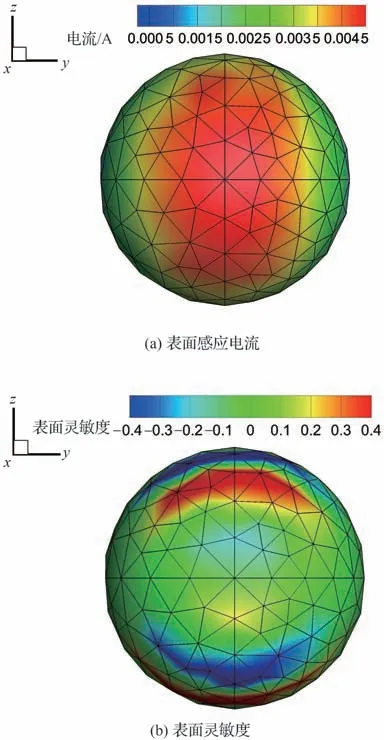
图8 球体算例的表面电流和表面灵敏度（f=1 GHz，VV）Fig.8 Surface current and surface sensitivity（f=1 GHz，VV）

图9 表面灵敏度计算中间量分布（f=1 GHz，VV）Fig.9 Intermediate quantity results（f=1 GHz，VV）

图10 类F22 战斗机表面灵敏度（沿鼻锥方向入射）Fig.10 Surface sensitivity of F22（incident towards nose）

图11 典型飞翼布局表面灵敏度（沿鼻锥方向入射）Fig.11 Surface sensitivity of flying wing（incident towards nose）

采用本文方法计算φ=0°，90°的表面灵敏度见图 6。与表面电流的分布特点相似，单一入射频点和入射角度的表面灵敏度具有正负交替的条纹，且正负条纹间隔约为λ4。

对比采用经典伴随方法和表面灵敏度方法求解设计变量梯度的计算效率和内存需求。计算采用Intel i7-9700 处理器8 核心并行计算。在计算效率方面，双锥体外形的阻抗矩阵Z填充用时11 s；仅计算z方向灵敏度时填充∂Z/∂r和Z矩阵用时35 s；除去求解控制方程和伴随方程的耗时，采用经典伴随方法计算36 个设计变量在180 个入射角度的梯度用时413 s，采用基于表面灵敏度的梯度计算方法用时19 s。在内存开销方面，经典矩量方法内存占用1.78 G，表面灵敏度方法内存占用16.72 G。可以看到，虽然偏导数矩阵∂Z/∂r的填充速度较慢，但由于基于表面灵敏度方法求解设计变量梯度时不需要填充扰动外形的阻抗矩阵，因此当设计变量较多时效率具有优势。

2）球体模型

球体模型半径r=0.2 m，计算入射频率f=1 GHz，单站散射垂直极化（VV），表面网格尺寸Δx=0.05 m；表面网格的总数N=197。

电磁波沿x轴负向入射时，采用经典伴随法（Adjoint_diff）和本文表面灵敏度计算方法（Adjoint_surface）求解模型在z方向的表面灵敏度dσ/dz，计算结果对比见图 7。可以看出2 种方法计算得到的梯度完全重合，证明本文表面灵敏度方法具有较高精度。表面感应电流和表面灵敏度计算结果见图 8，表面灵敏度空间分布特征和表面电流存在一定差异，对于表面感应电流，入射波直接照射的区域明显高于其他区域，而表面灵敏度的幅值与电流强度不直接相关，感应电流强的区域不一定具有更大的表面灵敏度，因此在优化过程中难以直接根据电流的分布特点判断区域的RCS 减缩潜力和方向，需进行表面灵敏度求解。

为进一步探讨表面灵敏度的特性，从式（9）可以看到，表面灵敏度dσ/dz的计算结果由∂σ/∂z、线性叠加得到，计算电磁波沿x轴负向入射、垂直极化时每一部分的空间分布特征，计算结果如图 9。可以看到，3 部分计算结果均具有明显的相位特征，空间分布与dσ/dz基本一致，与感应电流有差异显著。

3）F22 战斗机外形

分析典型战斗机的RCS 表面灵敏度特征，采用F22 战斗机外形，计算模型机身总长约19 m，半展长约7 m。考虑入射频率f=200 MHz，计算网格未知量数N=27 595。

沿鼻锥方向入射时水平极化（HH）和垂直极化（VV）的表面灵敏度计算结果见图 10。可以看出，与双锥体和球体算例相似，2 种极化方式入射时表面灵敏度均具有正负相间的特征，但2 种极化的表面灵敏度空间分布存在较大差异。对于垂直极化，战斗机机身的表面灵敏度大于机翼的表面灵敏度，且厚度较大的区域（如座舱）灵敏度更高，平尾边缘的灵敏度较大。对于水平极化，灵敏度较大的区域主要为机身和机翼的边缘，平尾的表面灵敏度较小，水平极化的灵敏在幅值上整体略小于垂直极化的表面灵敏度，且与几何的厚度没有明显关联。表面灵敏度的计算结果表明，灵敏度的空间分布与极化方式关联明显，极化方式的RCS 减缩需重点关注的区域有所区别。

4）典型飞翼外形

计算采用的飞翼布局根弦长约12 m，半展长约10 m，采用NACA65016 对称翼型生成。考虑入射频率f=200 MHz，计算网格的未知量总数N=28 086，分别计算入射波为水平极化（HH）、垂直极化（VV）时的表面灵敏度。

沿鼻锥方向入射时的表面灵敏度计算结果见图 11，其中水平极化的灵敏度明显高于垂直极化的灵敏度，2 种极化方式的灵敏度幅值的差异主要受当前状态的RCS 影响，当沿鼻锥入射时，两种极化的RCS 分别为RCSHH=-4.9 dB、RCSVV=-21.0 dB，RCS 与灵敏度正相关。垂直极化灵敏度较大的区域主要为中央体上下表面，厚度越大的区域灵敏度越大，该现象与F22战斗机的计算结果一致；而水平极化灵敏度较大的区域为机翼的前后缘，中央体前缘的灵敏度显著高于其他区域。

图12 分别为y=6 m 站位VV、HH 极化方式入射时表面灵敏度的计算结果，由于布局采用对称翼型，2 种极化方式入射时上下表面的灵敏度符号相反、幅值几乎一致，且都表现出了强烈的正负震荡特性，正负波峰的间隔约为入射波长的1/4。

图12 y=6 m 表面灵敏度分布Fig.12 Surface sensitivity at y=6 m

图13 为入射波水平极化（HH）时前向威胁扇区±30°角域的平均感应电流和表面灵敏度。可以看到，机翼前缘的平均感应电流较强，从前缘向后缘电流幅度逐渐降低。角域平均灵敏度仍表现出正负相间的特征，但由于不同角度入射时表面灵敏度存在相位叠加，平均表面灵敏度的明暗条纹不如单一角度入射时显著。图 14 为Slice 1、Slice 2 剖面（见图 11）的上下表面设计变量在前向威胁扇区的平均梯度，其中网格变形采用自由曲面造型技术（FFD），设计变量位置如图 11。虽然表面灵敏度呈现出显著正负交替的特征，设计变量梯度变化较为和缓。上下表面设计变量梯度不完全对称是由于设计变量上下表面在z方向的位置不完全对称造成。

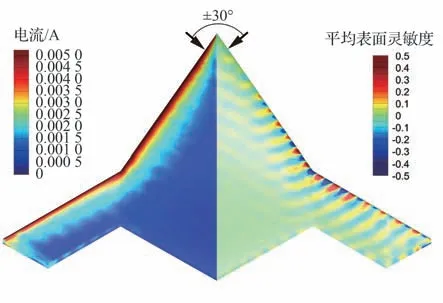
图13 角度平均感应电流和平均表面灵敏度（f=200 MHz，HH）Fig.13 Angle-averaged current and sensitivity（f=200 MHz，HH）

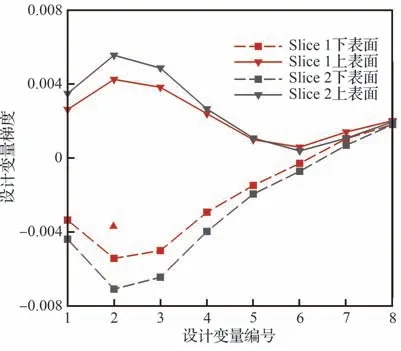
图14 Slice 1 和Slice 2 上下表面设计变量平均梯度Fig.14 Angle-averaged design variable gradients at Slice 1 and Slice 2

6 结论

提出了一种基于伴随方程和自动微分的雷达散射截面表面灵敏度计算方法，并结合基函数特点提出了适用于表面灵敏度的稀疏矩阵存储和矩阵-矢量相乘方法，降低了表面灵敏度的计算、存储开销。该方法可以通过一次阻抗矩阵偏导数求解得到所有网格点的表面灵敏度，当改变入射角度时，求解所有设计变量梯度的计算量约为8 次矩阵-矢量乘，极大提高了基于伴随方程的梯度计算效率。

计算典型入射条件下双锥体、球体、F22 战斗机、典型飞翼布局的表面灵敏度，证明了提出的表面灵敏度计算方法的准确性，该方法能够通过表面灵敏度快速完成设计变量梯度计算。表面灵敏度的空间分布特征受极化方式影响显著，具有明显的相位特征，可以为隐身优化设计提供指导。

本文仅研究了基于矩量法的表面灵敏度计算方法，但是矩量法的计算量和存储量较大，限制了其在电大尺寸问题中的应用，后续将进一步研究将该方法扩展到基于多层快速多极子算法的RCS 表面灵敏度求解中。