经济政策调控对我国股市波动的影响
■ 张国丽
(中国人民银行青海省分行 青海西宁 810000)
引言
经济政策调控(EPU)对股市有重大影响。Pastor &Veronese(2012)研究了经济政策调整对美国股市波动性的影响,发现政策变化增加了波动性、风险溢价和股票之间的相互联系[1]。Arouri(2016)等人调查EPU 对美国的影响股票市场回报率,发现EPU 的增加会显著降低股票回报率,这种效应在极端波动时期更强烈、更持久[2]。为了提供经济政策调控全面、定量的衡量标准,Baker & Bloom(2015)等人编制了世界主要经济体经济政策调控指数(EPU Index)[3]。该指数自推出以来,受到了众多学者的广泛研究,并得到了更广泛的认可。指数具有随时间变化的特征,具体来说当经济政策保持稳定时,EPU 指数相对较低,当经济政策变化频繁时,指数就会上涨。
作为金融业系统性风险的最终承担者,巴塞尔银行监管委员会(BCBS)1996 年开始要求银行业机构定期使用风险价值(VAR)进行内部控制和风险状况外部披露。当包括银行在内的金融机构在计算其所承受的市场风险的VAR 时,波动率的估计至关重要,直接影响着VAR 的计算结果。也可以说,观察股价波动非常重要,因为它对于资产定价和风险衡量至关重要,股市波动是聚合且高度持续的,虽然可以预测,但是准确预测是非常困难的。波动性研究有着比较悠久的历史,Engle(1982)通过引入ARCH 模型的思想,开启了波动性研究的新篇章[4]。Bollerslev (1986)在ARCH 模型的基础上加入了历史波动率,提出了GARCH 模型,更好地捕捉了股票收益波动的长记忆性[5]。此后,波动率的定量分析一直基于GARCH 模型。
目前,我国证券市场仍处于发展初期,股指波动性大幅高于工业化国家成熟市场。学者们希望通过更好地刻画股指甚至个股价格的波动性,提高整体证券市场的效率,最终建立一个有弹性、有抵抗力的、能够更好服务实体经济的证券市场,让投资者能更清晰地认识到他们承担的风险以及他们应该获得的风险溢价。然而,我国股市发展历史较短,对经济政策调控缺乏有效的反馈调整,因此,研究EPU 对我国股市波动的影响具有重要意义。同时,系统、深入地审视经济政策调控对我国股市的影响,有助于提高国家决策效率、加大市场监管力度、稳定股市发展。本文选择使用GARCH 模型来研究EPU 对我国股市波动的影响,
一、文献综述
(一)我国股市的波动性
由于波动性是经济表现的晴雨表,它为政府和投资者感知市场风险提供了一定的判断依据,因此了解我国股市不同板块公司股价(或收益率)波动所表现出的复杂联动效应意义重大。Zhang(2011)等人研究了股指期货的推出对我国股市波动的影响[6]。Jiang&Chen(2016)研究了美国经济变量对我国股市随时间波动的影响[7]。Wen&Xiao(2018)等人使用非线性自回归分布滞后(NARDL)模型[8],Diks & Pachink 在总体和部门层面上研究石油价格与我国股市之间的非线性协整和非线性因果关系[9]。实证结果表明石油价格与我国股市之间不存在显著的非对称协整效应,然而石油价格与我国股市之间存在显著的非线性因果关系。Wen&Cao(2021)的结果表明,股票市场和大宗商品市场之间存在高度依赖[10]。我国股市平均是溢出效应的净受益者,有色金属和化工行业对股市影响巨大。随着时间的推移,总波动性溢出的程度会发生变化[10]。在发生重大危机之后,市场波动相关性就会增强。自2019 年以来,股票市场对大宗商品价格的影响急剧扩大。
(二)股票市场的波动性
Zhou(2018)讨论了波动性的含义。波动率主要用标准差或方差来表示。在经济学术语中,波动性是指金融资产价格或资产投资回报率变化的剧烈程度,是不确定性的衡量标准[11]。本质上,波动性是市场对各类信息的综合反映,它既包括市场价格形成机制中的有效信息,也包括交易系统的环境噪声,还夹杂着投资者的情绪因素。一般来说,波动性越高,金融资产的风险越高。就股票市场而言,波动性表现为股票价格变化的频率和幅度。两者越大,波动性越高,两者越小,波动性越低。
股票市场的波动性一直是许多学者研究的焦点。例如Blank-Scholes 提出的期权定价模型,这些模型假设市场回报服从正态分布,并认为波动性是恒定的。Fama(1965)通过他的研究发现了峰值和股票价格厚尾的本质[12]。Morgan(1976)发现了时间序列的异方差性[13]。20 世纪60年代,Mandlebrot(1963)发现波动性是聚合性的,即大幅波动伴随着大幅波动[14]。Salisu&Gupta(2020)使用GARCH-MIDAS(混合数据抽样的广义自回归条件异方差变量)模型研究金砖国家(巴西、俄罗斯、印度、我国和南非)对股市波动的反应[15]。研究发现,对波动性的不准确预测可能导致金融市场定价错误、业务对冲过度或不足以及资本预算决策不正确,从而对收益和现金流产生重大影响。因此,监测和建模股市波动不仅对投资者和企业决策者很重要,而且对政策制定者评估金融基本面和投资者情绪也很重要。
此外,影响股市波动的原因还有很多。例如,Ngassam(2002)认为止损限价降低了股票收益的波动性,同时也发现股票止损限价并没有降低股票收益的波动性[16]。Engle&Rangel(2008)研究了40 多个国家的股票市场,发现宏观经济政策影响股票市场的波动[17]。Safi 和Sigurdsson(2010)发现,减少股票卖空限制并不能减少股价波动[18]。Henry(2009)发现短期利率变化对股票收益的影响[19]。Girardin&Joyeux(2013)提取了我国A 股和B 股市场的长期波动性[20]。他们使用混合数据采样(MIDAS)方法。尤其是我国A 股市场,直到2001 年,一直以投机为特征。然而,2001 年以后B 股市场也表现出投机特征。因此,结果表明,长期股票波动有时是由通货膨胀而不是实际活动来解释的。Rao&Yue(2017)等人研究了EPU 对我国未来波动性的影响[21],作者利用GARCH-MIDAS 模型探讨了GEPU 指数的增量预测信息及其对我国股市波动性的影响。研究结果表明,我国及世界经济和政策调控的宏观信息影响我国股市的波动。根据科尔尼和戴利Kearney & Daly(1998)提出股票市场回报的条件波动性与金融和商业周期因素的条件波动性相关[22]。使用广义最小二乘(GLS)估计方法通过一般到具体的建模策略,描述了股票市场回报的条件波动率方程以及确定模型中所有变量的条件波动率方程。
(三)EPU 与股市波动性之间的联系
EPU 指数吸引了众多作者的关注。Baker (2015)等人利用报纸报道的频率构建了可以衡量经济政策调控的EPU指数[3]。此外,Liu &Zhang(2015)采用了Corsi(2008)提出的异质自回归实现波动率(HAR)框架[23][24]。EPU 指数可以极大地提高模型的预测性能。Wu & Xie (2021)使用CARR 混合数据采样(CARR-MIDAS)模型框架通过考虑日内信息来研究EPU 对我国股市波动的影响[25]。实证结果表明,我国EPU(CEPU)和全球GEPU 对我国股市的长期波动都有相当大的不利影响。此外,他们发现将CEPU 和GEPU考虑在内可以显著提高预测我国股市波动的能力。
Liu & Zhang(2015)在现有波动率预测模型中添加EPU 是否可以提高预测能力问题,在之前的研究中尚未得到解决[23]。此外,它们还显示样本外数据,这会产生额外的财务影响,因为样本外波动性预测对于投资组合配置和风险管理至关重要。他们还通过使用标准普尔500 指数的5 分钟高频回报来研究EPU 的作用,以确定每日的市场波动性,并使用八个每日波动性(RV)演变流行模型来研究EPU 的作用。无论使用哪种模型,样本证据都表明先前的EPU 对当前RV 的影响显著为正。
Kang & Ratti(2013)使用结构性VAR 模型来研究结构性石油冲击、经济政策调控和实际股票回报之间的关系[26]。研究结果显示,石油市场的特定需求冲击对24 个月后经济政策调控变化的影响超过30%,长期来看这一比例将增长至58%。经济政策的调控导致实际股票收益长期变化的19%,而结构性石油冲击则导致实际股票收益长期变化的32%。因此,对于不同行业而言,政策调控会压低石油行业的长期回报、短期内汽车和零售行业的回报以及长期黄金行业的回报。
Mei&Zeng(2018)等人首先考察美国EPU 指数是否有有用的预测信息来帮助预测欧洲股市,例如英国、德国和法国市场,使用样本外统计检验,得到几个结论。首先,欧洲国家的EPU 指数似乎对预测这些股票市场的波动没有太大帮助;其次,他们在基准模型中添加了美国EPU 作为附加变量,并确定该模型通过包含美国EPU 指数可以获得更高的预测精度,这有力地支持了美国EPU 指数包含对欧洲股票有用的预测信息的观点市场;第三,基于美国的扩张和衰退,作者发现美国EPU 指数可以提供更多相关的预测信息,并且可以比扩张期间显著提高欧洲股市在衰退期间的预测能力[27]。Chen(2018)等人应用GARCH-MIDAS 模型来研究全球经济政策调控(GEPU)中包含的信息是否有助于预测黄金期货收益方差的短期和长期组成部分[28]。调查结果显示,GEPU 对全球黄金期货市场未来月度波动性做出了积极且重要的预测。Mishra & Debata (2020)研究探讨了纯粹订单驱动的新兴股市中经济政策调控(EPU)与股市波动性之间的动态关系[29]。由于EPU 与波动性之间的非线性关系,本研究使用一系列GARCH 模型来反映政策调控对股市波动性的影响。Wu & Hsueh(2016)调查了2003 年至2004 年期间九个国家的经济政策调控与股市出口和增长之间的因果关系[30]。实证结果表明,并非所有国家都是一样的,当政策变化公布时股市下跌的理论预测并不总是准确的。这项研究为印度、意大利和西班牙的股市领先假说提供了证据,但在英国则不然,不能排除英国的经济政策调控领先假说。
(四)GARCH 模型
Engle(1982)提出用ARCH 模型来分析时间序列的异方差性[4]。Chen(2014)发现ARCH 模型存在以下缺陷。首先,ARCH 模型假设波动性由扰动信息的历史数据值的二次平方项决定,这意味着它对正向和负向价格扰动的响应相同,而现实生活中情况并非如此;其次,高阶ARCH 模型的应用限制过于严格,对相关参数要求非常高,使它们在应用中受到很大限制,并且不能很好地拟合超峰度的实际数据;第三,虽然ARCH 模型正式描述了条件方差,但解释条件方差的真正原因很困难。第四,ARCH 模型对收益序列中的奇异值扰动现象不敏感,因此波动率的预测结果往往偏高;随后,Bollerslev(1986)提出了GARCH 模型,GARCH 是专门为金融数据量身定制的回归模型[5]。一般来说,波动率研究和预测选择GARCH 模型进行实证分析,它可以帮助投资者做出更好的判断。GARCH 已优化升级到新的版本,例如:IGARCH 模型(Integrated GARCH,Bollerslev(1986))、EGARCH 模型(Exponential GARCH,Nelson(1991))、TGARCH模型(Threshold GARCH, Zakoian(1994))等[5][31][32]。
在市场因素对股市波动性的研究中,大多数作者都选择使用GARCH 模型进行分析。Zhang& Chen 等人(2011)研究了股指期货在我国的引入对股市波动性的影响,随着沪深300 指数的引入,股市波动性在短期内有所增加,但随着时间的推移,这种影响趋于减弱。Li(2012)利用GARCH(1,1)模型比较了开放式基金进入股市前后股市波动的特征,表明开放式基金的加入增强了对条件方差的影响的股票市场回报,股市波动的持续时间增加,平滑度降低[33]。Shenbagaraman(2003)利用GARCH 模型族研究了印度S&PCNXNifty 指数期权合约上市后对现货市场的影响[34]。Yue(2001)利用GARCH 族模型研究了我国股票市场的收益,结果表明,我国股票市场的收益不仅存在条件异方差性,而且存在聚集性、持续性和不对称性[35]。Katsiampa (2017)使用GARCH 系列模型探索了关于比特币价格数据拟合的最佳条件异方差模型[36]。AR-CGARCH 模型被认为是最好的,强调了包括条件方差的短期和长期组成部分的重要性。
DONG(2017)在GARCH 模型中引入虚拟变量来分析股指期货引入后对股票现货市场波动性的影响,结果表明,上证50 和中证500 股指期货的引入都降低了股指期货的波动性,然而现货市场相应标的指数跌幅却很小[37]。此外,Liu 和Hung(2010)验证了非对称GARCH 模型在预测股市回报波动方面具有更高的准确性[38]。So &Yu(2006)研究了七个GARCH 模型在不同置信水平下估计风险价值的效果, 结果表明,在估计1% 的风险价值时,固定GARCH模型和部分集成的GARCH 模型都击败了风险矩阵模型[39]。虽然大多数收益序列都具有肥尾分布并满足长记忆特性,但在计算风险值时,更有必要考虑具有肥尾误差的模型。股票市场数据中也可能出现不对称行为,其中T 误差模型在估计多头头寸1% 的风险价值方面优于常规误差模型,但在空头头寸方面则不然。在汇率数据中,没有发现这种差异。
2008 年全球金融危机以来,EPU 水平不断上升,这使得探讨EPU 对我国股市波动的影响成为一个有趣的话题。此外,研究经济政策调控对我国股市的影响,有助于我们了解股市异常波动,也有助于理解宏观经济波动。本论文将用EPU 指数衡量经济政策调控Baker &Bloom (2015)[3],分析EPU 对我国股市波动性的影响。
二、模型设定
(一)ARCH 和GARCH 模型
Engle(1982)提出ARCH 模型来解决传统计量经济学第二个假设中时间序列变量方差恒定所带来的问题[4]。而它的主要核心就是方差在t 时刻受到扰动项的影响,ARCH(q)模型采用如下形式表示。
平均方程:
方差方程:
ARCH 模型提出后,在经济金融领域取得了巨大成功,但也存在很多不足。Zhou(2018)提到,ARCH 模型假设波动性取决于扰动信息历史数据的二次平方项,即对正负价格扰动具有相同的响应,这与现实生活存在显著差异[11]。其次,高阶ARCH 模型的应用限制太大,对相关参数的要求非常高,因此其应用受到很大限制,不能很好地拟合超峰度的现实数据。第三,ARCH 模型形式化地刻画了条件方差,但很难解释条件方差的真正原因。最后,ARCH 模型对收益序列中的奇异值扰动现象不敏感,导致波动率的预测结果往往偏高。
Bollerslev(1986)年对ARCH 模型进行了修改和增强,进一步放宽了ARCH 过程的使用条件,可以将其视为拟合无限形式的ARCH 模型[5]。条件方程如下。
平均方程:
方差方程:
GARCH 模型开创了ARCH 模型的时代。但仍然没有解决早期ARCH 模型中条件异方差依赖于随机扰动大小而不考虑正负的问题。本论文指定的GARCH 模型为:
平均方程:
方差方程:
(7)式中为条件方差,q 为ARCH 的阶数,是自回归GARCH 的阶数,是个EPU 的顺序。为了确保条件方差为正,。
(二)数据来源
本文选取上证指数和深圳成指来代表我国股市的波动性,使用来自商业分析和数字经济中心的EPU 数据。使用并对比Bloom,Baker& Davis(2015)中的分析方法,本文采用的我国EPU 指数与Bloom,Baker& Davis 采用的我国EPU 指数相比具有许多优势[3]。首先,在VAR 实践中,该指数优于SCMP 指数;其次,为了供金融专业人士和普通公众使用,网站创建了每日指数以及其他针对特定政策的EPU 指数;最后使用各种报纸进行反复检查,以确认EPU指数在质量上不受媒体的影响。本文选取2010 年1 月4 日至2021 年9 月30 日(不含节假日等)共2857 个观测数据,使用EViews10 对数据进行分析处理。上证指数和深圳成指数据取自CSMAR 数据库,我国经济调控指数(EPU)数据取自网站(https://cbade.hkbu.edu.hk/epu-mainland-china/)。为了消除效应量纲效应,将上证指数和深证指数数据分别乘以10,得到上证指数调整后的收益和深证指数调整后的收益,EPU 数据未经处理。
三、实证分析
(一)描述性分析
由图1 可见,上证成指在2014 年至2016 年经历了一些波动,经过两年的“沉寂期”股市又出现了几次大的波动,分别是2018 年、2019 年上半年和2020 年。此外,2010 年至2013 年中期股市的波动性较为温和,但这一时期的波动相对于2016 年至2017 年的平稳时期更大。最后,2021 年股市波动较小,没有出现极值。
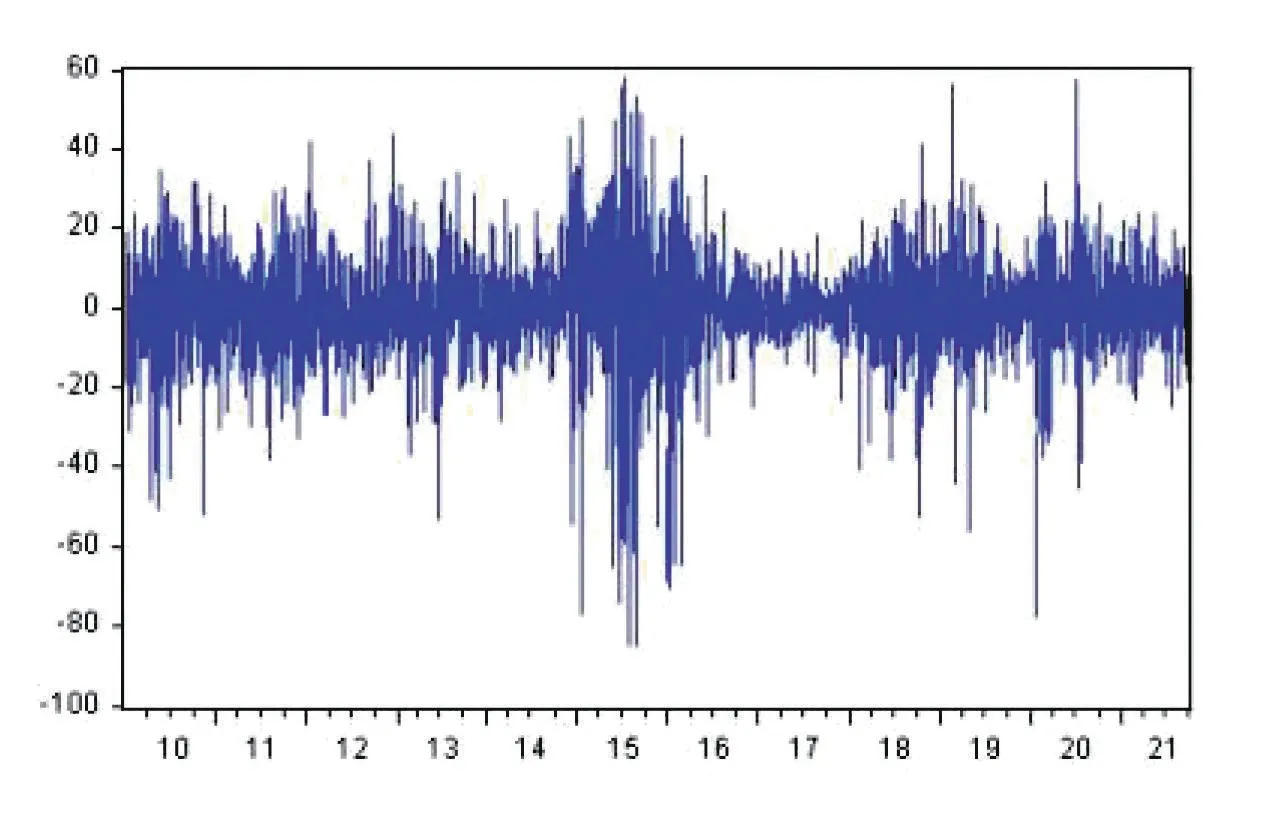
图1 上证指数日调整收益:2010~2021 年
由图2 可见,深圳成指2014 年至2016 年的波动趋势与上证指数相似,但2010 年至2013 年的波动也更为剧烈。2010 年和2013 年出现了大幅波动,这是由于2010 年资本市场政策调整、创新举措较多,1 月8 日开始的融资和融资量、股指期货获批,被市场解读为利好。2013 年是全年暂停IPO 的一年,而且2018 年到2020 年的波动也比较大,其原因与上证指数类似。但与上证指数不同的是,深圳成指2021 年跌幅更大。
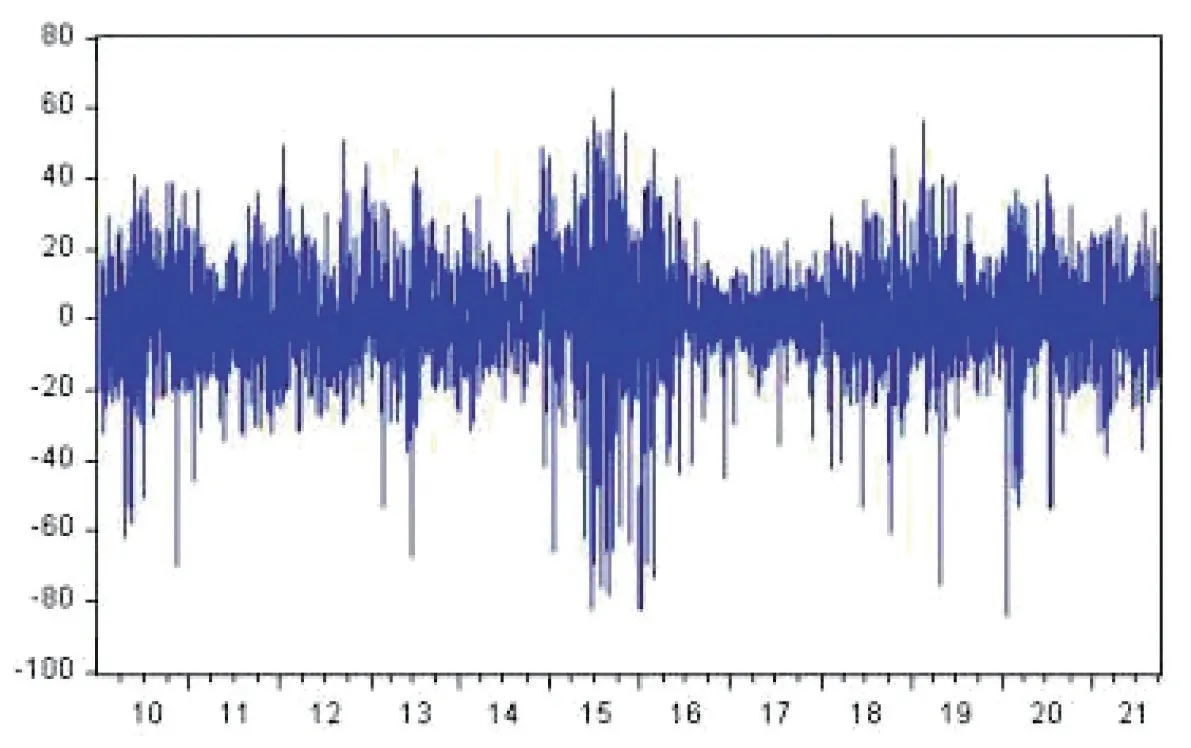
图2 2010~2021 年深圳成指每日调整回报率
从两个股指的波动趋势可以看出,2017~2018 年时间段内两个系列的波动较为平滑,且均值大于且接近于0,表明当时我国股市的整体波动性不是很高,但深圳成指的波动比上证指数更大。而且,通过横向比较上证指数和深证指数的波动趋势,可以看出,两个指数的波动趋势基本一致。
我国EPU 指数日收益率如图3 所示,我国的EPU 波动性在经济衰退期间达到顶峰。有些年份波动较大,如2011年以后经济受到欧元区危机的影响;2018 年中美贸易战。此外,周一和周五EPU 数据的大幅波动表明,我国的经济政策倾向于在周五公布,这是因为一般证监会的经济政策都在周五下午3 点后公布。总体来看,2011 年以来我国EPU 指数波动趋势缓慢下降,而其他年份我国EPU 指数值波动相对稳定。另外,EPU 的hp 滤波显示,2010 年2012年以前均高于均值,2012 年以后则基本低于均值。
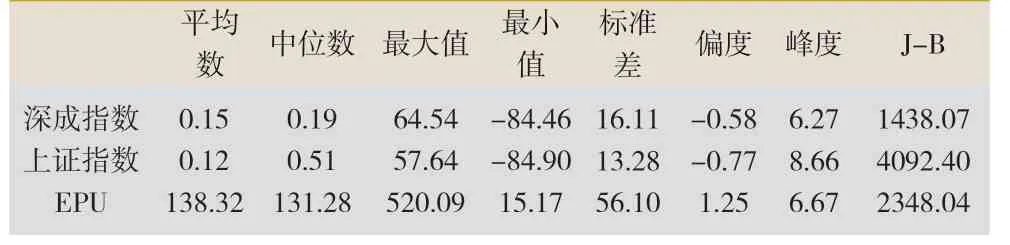
表1 股票指数和经济政策调控指数的描述性统计
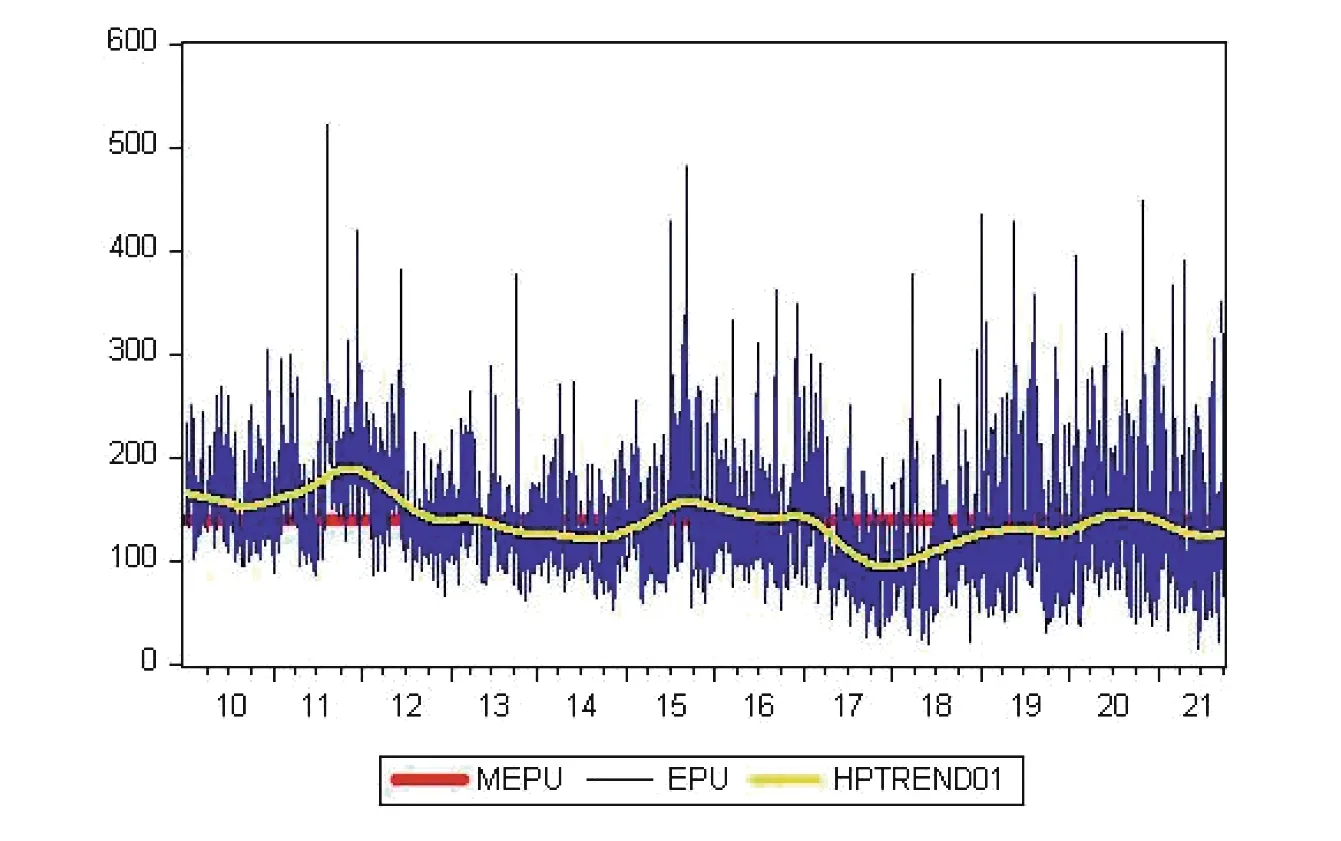
图3 2010~2021 年我国经济政策调控指数日回报率
由上表可见,最大值和最小值之间的差异也比较大,这表明上证指数和深证指数的集中度都比较弱。经济政策调控最大值与最小值差距较大,表明样本期内经济政策调控指数波动较大。上证指数的标准差最小,表明该系列的离散性最小,EPU 的最大标准差表明该序列更加离散。
从偏度和峰度来看,上证指数和深股指数收益波动率的偏度均为负值,呈现出左偏趋势,这是大多数国际证券市场的典型特征。上证指数和深证指数的峰度分别为6.27和8.66,峰度均大于3,表明两个指数系列均存在显著的尖峰现象。另外,经济政策调控的偏度值大于0,峰度值大于3,这表明EPU 数据存在右偏分布和尖峰现象。可以看出,上证指数和深圳成指收益序列均具有峰高肥尾的特征,并且这一特征在股市中更为显著。
由表2 可见:上证指数、深证指数之间的相关性为0.927,相关系数大于0.7 以上,表明上证指数和深证指数均具有强相关性。EPU 指数与深成指数的相关系数为-0.005,呈负相关。当深成指数值较大时,经济政策调控值较小,但两者之间的负相关性较弱。深成指数和EPU之间相关性也较低。
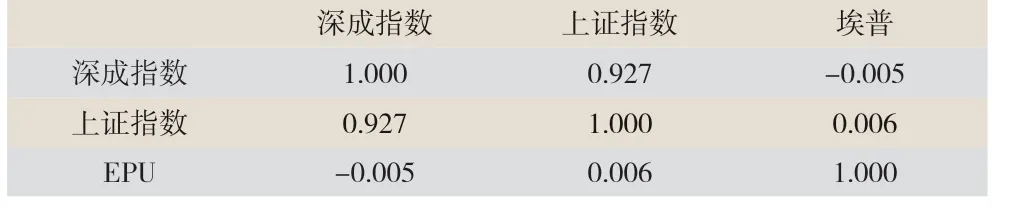
表2 描述股票指数与EPU 之间的相关性
(二)结果及分析
(1)GARCH 模型(SSE)实证分析结果
根据表3 的回归结果,可得均值方程:
方差方程:
从均值方程可以看出,上证指数的滞后收益系数为0.0249,该值较小,p 值未能通过5%显著性水平的显著性检验。这说明上证指数本期收益率与前期收益率相关性并不显著。这可能是由于本文使用的样本数量不足,以及市场干扰因素相对较多导致的(Wang,2021)[10]。Cheng(2014)的结果表明AR(1)也不足以模拟上证指数的回报[40]。从方差方程中可以看出,残差项的平方系数为0.056,通过了5%显著性水平的显著性检验,表明市场消息对市场价格波动影响较小,信息传播良好。波动率滞后项的系数为0.938,数值较大,在5%的显著性水平上通过了显著性检验。这表明过去一段时间的信息对市场波动的影响是相对持久的,这也证实了我国股市波动性的聚集效应。
从经济政策调控对波动性的影响来看,随着经济政策调控滞后数的增加,该因素对波动性的影响程度变小。EPU(-1)项的系数为0.196,表明经济政策调整对上证指数收益率的波动性有正向贡献,系数t 检验中的p 值为0,小于0.05,表明它通过了5%的显著性检验。EPU(-2)项的系数为-0.125,表明经济政策调整对上证指数收益波动具有抑制作用。此外,系数t 检验的P 值为0.0128,小于0.05,通过了5%显著性水平检验,表明经济政策调整对上证指数收益波动具有显著的抑制作用。EPU(-3)项的系数为-0.12,表明经济政策调整对上证指数收益波动性有抑制作用,系数t 检验中的p 值为0.668,大于0.05,表明未通过5%显著性水平检验。这表明,随着经济政策调控滞后期的增加,对上证指数收益波动的影响变得不显著。EPU(-4)项的系数为0.09,表明经济政策调整对上证指数收益波动性有正向贡献,系数t 检验中的P 值为0.1521,大于0.05,表明它没有通过5%显著性水平检验。EPU(-5)项的系数为-0.041,表明经济政策调整对上证指数收益波动具有抑制作用,系数t 检验中的p 值为0.2884,比0.05 大,表明未通过5%显著性检验。
EPU 对上证指数回报的影响随着时间的推移而减弱。总体而言,从变量EPU 的滞后期系数来看,经济政策调控因素对上证收益率波动的影响方向随时间存在交替变化。
(2)GARCH 模型(SZI)实证分析结果
由表4 可知:深成指数滞后收益系数为0.02227,且未通过5%显著性水平的显著性检验,表明深成指数本期收益与上期收益之间的相关性不明显。这与实际情况不符,可能是由于本文使用的样本量不足所致。
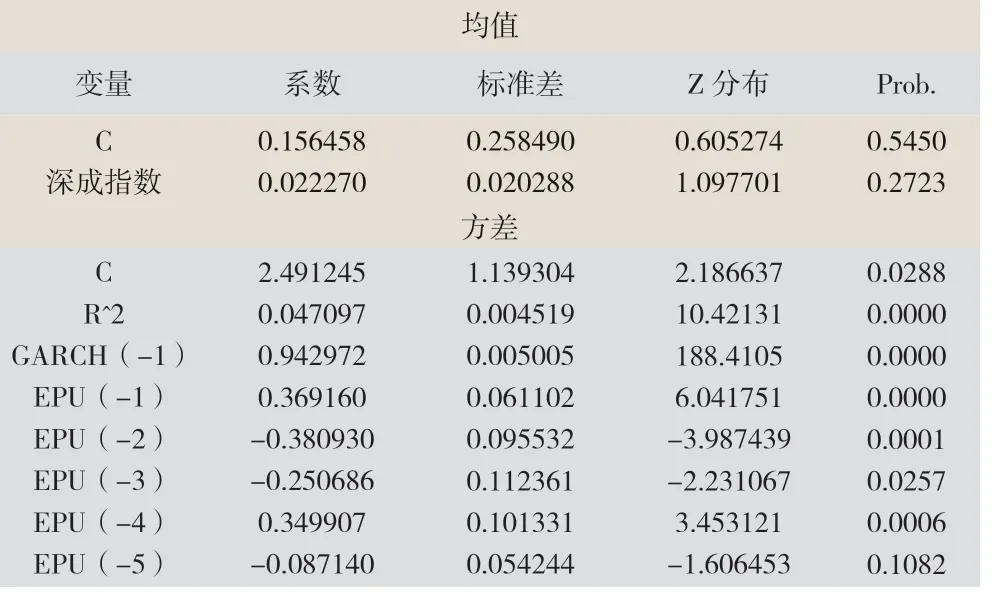
表4 GARCH 模型与SZI 的经验结果
从方差方程中可以看出,残差项的平方系数为0.047,接近5%表明市场消息对市场价格波动影响较小,信息传播良好。波动率滞后项的系数为0.943,数值较大,在5%的显著性水平上通过了显著性检验。这也证明了深圳成指的波动是聚集性的。另外,残差平方项和一期滞后方差项的系数均小于1,表明模型满足稳定。总体而言,从经济政策调控对波动性的影响来看,随着经济政策调控滞后数的增加,该因素对波动性的影响程度越来越小,但一定滞后期影响程度会突然加大,说明政策有调控区间。
EPU(-1)项的系数为0.369,表明经济政策调整对深圳成指收益波动性有正向贡献,系数t 检验的P 值为0,小于0.05,通过了5%显著性水平检验。EPU(-2)项的系数为-0.257,表明经济政策调整对深圳成指收益波动有抑制作用,t 检验中的p 值为0.0001,小于0.05,通过了5%显著性水平检验,表明经济政策调控因素对深圳成指收益波动具有显著抑制作用。EPU(-3)项的系数为-0.251,表明经济政策调整对深圳成指收益波动性有抑制作用,t检验中的p 值为0.026,小于0.05,通过了5%显著性检验;这表明,随着经济政策调控滞后期的增加,对深圳成指回报率的波动性有显著影响。EPU(-4)项的系数为0.35,表明经济政策调整对深圳成指收益率的波动具有正向促进作用,t 检验中的p 值为0.0006,小于0.05,通过了5%显著性水平检验。然而,EPU(-5)项的系数为-0.087,表明经济政策的调整对深圳成指收益的波动具有抑制作用,t 检验的P 值为0.1082,大于0.05,未通过5%显著性水平检验。
随着时间的推移,EPU 对股票回报的影响越来越小。通过统计描述分析,得出深股通收益波动具有波动集群的特征,即过去的股市波动影响未来的走势。上证指数和深成指数回报序列稳定,不服从正态分布。此外,比较经济政策调控对两地股票波动性的影响,我们发现EPU(-1)和EPU(-2)对上证指数股票的回报率有显著影响,但深交所股票的回报率受EPU(-1)、EPU(-2)、EPU(-3)和EPU(-4)影响显著。这意味着经济政策的调整对深交所股票回报的影响更为深远。
四、结论和建议
首先,研究经济政策调控对股市波动的影响对于我国经济发展和金融稳定有积极意义。其次,股票市场作为交通便利、公众广泛参与的交易场所,能够准确、实时地反映宏观经济运行情况,研究经济政策调控与股票市场的联动效应可以解释政策对股市的影响。最后,实证结果可以为股票市场参与者提供投资建议,并为宏观调控、决策效率、市场监管、股市发展稳定提供一定的参考。

