置信区间宽度等高线图在线性混合效应模型样本量规划中的应用*

刘 玥 徐 雷 刘红云 韩雨婷 游晓锋 万志林

(1 四川师范大学脑与心理科学研究院, 成都 610066)(2 应用实验心理北京市重点实验室; 3 北京师范大学心理学部, 北京 100875)(4 北京语言大学心理学院, 北京 100083) (5 南昌师范学院数学与信息科学学院, 南昌 360111)

1 引言

近年来, 心理学研究者对学术不端和研究可重复性问题的讨论日趋激烈。国内外越来越多的学术期刊推行预注册(pre-register)制度, 能够有效避免根据结果决定是否继续收集数据的不良行为(例如p-hacking), 促进科研过程和结果的公开透明, 提高研究的可重复性(Nosek et al., 2022)。预注册时,对被试量、试次数等与研究设计相关的要素需有明确规划和充分理由。如何针对特定的统计模型开展样本量规划, 是心理学研究者关心的问题。本研究基于线性混合效应模型, 探索使用模拟方法结合检验力和效应量准确性开展样本量规划的范式, 并通过开发直观的置信区间宽度等高线图, 方便应用研究者确定符合要求的被试量和试次数, 为开展研究设计、保证研究质量提供方法支持。

1.1 线性混合效应模型的样本量规划问题

随着研究问题的深入和数据收集手段的进步,含有随机效应的刺激和嵌套结构的设计越来越普遍。例如, 心理语言学实验研究通常会使用词语作为刺激, 但不同词语诱发的反应速度不同, 会造成观察到的实验效应有一部分是由不同的词语刺激引起的(Barr et al., 2013)。此时, 以传统方差分析为代表的方法由于混淆了实验效应与随机效应, 会导致第I 类错误和检验力的估计偏差(Barr et al., 2013;Judd et al., 2017)。线性混合效应模型(Linear Mixed-Effects Models, LMEMs)可以避免由于对被试接受的同一条件下所有刺激求均值等方式(如,重复测量方差分析)造成的信息损失, 且同时灵活考虑不同原因(如, 刺激随机取样、被试嵌套结构等)造成的随机效应。因此, LMEMs 在心理学实验中的应用越来越广泛(Barr et al., 2013; Brauer & Curtin,2018; Judd et al., 2017; Lee, 2018)。在web of science中检索近5 年的心理学实验类论文, 使用LMEMs约是使用方差分析的1.5 倍。

然而, 目前国内LMEMs 的应用还很少。例如,2020～2022 年我国心理学顶刊《心理学报》上发表的181 篇实验类文章中, 仅9 篇使用了LMEMs, 且其中的5 篇没有阐述确定样本量的理由, 3 篇应用G*power 近似得到所需样本量, 仅有1 篇应用simr软件包采用模拟方法基于检验力分析确定样本量。制约该模型广泛应用的一个重要原因是, 设计中随机效应的增加带来了模型复杂程度的增加, 导致常用的样本量规划软件(例如G*power 等)不再适用,研究者对基于LMEMs 如何科学地规划实验设计,设置合理的被试量和试次数感到无所适从, 急需方便易用的程序或图示, 指导样本量规划。

1.2 基于检验力分析规划样本量

传统样本量规划主要基于虚无假设显著性检验(Null Hypothesis Significance Test, NHST)的检验力分析, 要求样本量必须使检验力达到预设标准。检验力分析可分为公式推导方法和基于蒙特卡洛模拟方法(例如Arend & Schäfer, 2019)。公式推导方法含有关于分布的强假设, 当数据不符合时可能得到有偏差的结果(Judd et al., 2017)。基于蒙特卡洛模拟的方法是在预设的参数下基于特定模型重复生成数据, 再基于模拟数据估计参数, 统计所有重复中得到显著性结果的比例。其优势在于不需要推导参数分布, 能够处理非正态分布的数据, 并且可以灵活定义模型。一些学者已经开发了成熟的R 软件包(如 simr)应用蒙特卡洛模拟的方式计算LMEMs 的检验力(Green & MacLeod, 2016)。

为了方便应用研究者基于检验力分析确定适用于嵌套数据分析的合适样本量, 一些研究者在模拟方法的基础上, 开发了直观的图示以及配套程序,展示不同样本量情况下的检验力, 为样本量规划提供参考。应用最广的是以样本量为横坐标, 检验力为纵坐标的折线图(例如Kumle et al., 2021)。研究者根据预设检验力做出水平线, 与折线交点所对应的横坐标就是满足要求的最小样本量。Murayama等(2022)还开发了生成检验力折线图的在线程序。但是, 嵌套结构的数据需要确定两个水平样本量,不同实验设计下增加不同水平样本量的成本不同。折线图仅能固定某个水平样本量, 以另一个水平样本量为横坐标生成, 无法同时呈现两个水平样本量与检验力的关系。Schultzberg 和Muthén (2018)将水平1、2 样本量分别作为横、纵坐标, 用阴影区域表示符合检验力要求的两个水平样本量组合范围。Baker 等(2021)提出了检验力等高线图, 将相同检验力的两个水平样本量组合的点连成等高线, 用多条等高线表示不同检验力水平。综上, 对于嵌套数据, 研究者需要在同一个图内观察到两个水平样本量在检验力上的补偿关系, 并在考虑实验成本的基础上综合权衡, 得到合适的各水平样本量。

1.3 基于效应量准确性分析规划样本量

以上总结的样本量规划图示仅考虑了检验力。但是, 随着学术界对NHST 的批判, 美国统计协会发表了关于谨慎使用NHST 的声明, 强调应避免仅报告显著性, 而应同时报告效应量(Wasserstein &Lazar, 2016)及其区间估计的结果。因此, 一些学者提出应基于效应量准确性分析开展样本量规划。

效应量准确性分析的核心是控制效应量置信区间(Confidence Interval, CI)的宽度, 越窄表明其估计越准确(Maxwell et al., 2008)。有研究根据期望的CI 上下限, 倒推可接受的最大CI 宽度(Usami,2020)。例如, 在效应量的点估计值为0.5 的情况下,计算得到其95%置信区间(以下简称“95% CI”)宽度为0.6, 则95% CI 约为[0.2, 0.8]。根据Cohen (1988)的标准, 该区间涵盖了效应量小、中、大的条件(0.2,0.5, 0.8), 估计精确性差(Maxwell et al., 2008;Usami, 2020)。有的研究直接根据不同CI 宽度计算对应的最小样本量(例如Kelley & Rausch, 2006)。总之, 目前关于如何确定可接受的最宽CI 宽度仍未形成一致结论(例如Kelley et al., 2018)。

为了方便应用研究者基于效应量准确性分析确定适用于嵌套数据分析的样本量, Hecht 和Zitzmann (2021)提出了基于被试数和时间点的总体表现图, 分别以二者作为横、纵坐标, 通过收敛比例, 参数估计偏差等指标计算模型拟合的综合表现得分, 并以色块区分不同得分。研究者可以根据色块, 权衡得到合适的样本量组合。但该图并未考虑检验力, 并且色块仅表示综合得分, 具有一定的主观性, 研究者无法从图中清晰了解所关心的参数估计的准确性。

1.4 问题提出

综上, 针对嵌套数据的样本量规划需同时保证检验力和效应量准确性达到要求。然而, 已有的方法、程序或图示大多只基于其中一个目的展开(例如Arend & Schäfer, 2019; Kumle et al., 2021; Usami,2020), 尚没有图示能够方便研究者同时考虑两方面要求规划样本量。因此, 本研究提出CI 宽度等高线图, 采用蒙特卡洛模拟方法进行检验力和效应量准确性分析, 在图中同时呈现两个水平样本量不同组合下的检验力和CI 宽度情况。由于CI 宽度尚没有统一标准, 本研究结合已有研究的两种思路, 提供不同CI 宽度下的样本量, 建议研究者结合期望的CI 上下限推出可接受的最宽CI 宽度, 进而综合检验力分析结果确定被试量和试次数的理想结合点。

此外, 在以心理学实验研究为背景的样本量规划中, 研究者普遍关注基于实验效应中固定效应的样本量规划(Lee, 2018), 未关注基于被试变量对实验效应的调节效应的样本量规划。然而, 随着心理学个体差异视角研究的深入, 越来越多的研究开始探索不同类型个体间的实验效应是否存在差异。例如, 蒋元萍等(2022)发现, 积极情绪和消极情绪状态下被试(被试调节变量)的跨期决策行为(实验效应)存在显著差异。这类研究需要样本量规划满足被试变量调节效应估计准确性的要求。因此, 本研究以典型的被试内重复实验设计为背景, 基于LMEMs, 分别探讨基于被试内变量的实验效应和被试间变量的调节效应的样本量规划问题。

本文首先在多层线性模型框架下重构模型, 以更好适应实验设计在不同层级加入自变量(控制变量)的需要。然后, 说明生成CI 宽度等高线图的流程及其函数。最后, 分别基于被试内变量的实验效应和被试间变量的调节效应进行模拟研究, 考察实验效应、随机斜率、被试变量类型如何影响评价指标结果和CI 宽度等高线图, 并说明如何根据结果推荐合适的样本量。

2 心理学实验研究中的线性混合效应模型

LMEMs 的一般形式可见Williams 等(2021)的文章。在多层线性模型的框架下, 可对其重新定义。以刺激嵌套于实验条件的被试内实验设计为例, 假设刺激没有重复(Barr et al., 2013; Lee, 2018)。水平1 表示试次(trial)水平, 水平2 表示被试水平, 试次嵌套于被试。随机斜率模型(模型1)可表示为

其中,Yji表示连续的结果变量(j= 1,…,J表示试次,i= 1, …,I表示被试),Xji表示实验效应的虚无编码,β0i和β1i分别表示被试的随机截距和随机斜率,即不同被试基线水平和实验效应的不同,I0j表示刺激的随机截距(不同刺激的效应不同)。γ00和γ10分别表示被试随机截距的均值和随机斜率的均值,其中γ10是实验效应的固定部分, 是重点考察的效应量指标。u0i,u1i,rji分别表示水平2 截距、斜率的随机部分和水平1 的残差。模型假设,刺激的随机截距I0j～N(0,ω002)。

多层线性模型的优势在于能够方便地在不同水平加入解释变量。例如, 可在水平2 加入自变量Wi, 用于解释随机截距和随机斜率存在个体间差异的原因(模型2)。

其中,Wi表示被试变量,γ01表示被试变量对随机截距的影响,γ11表示被试变量对随机斜率的影响,也可看作水平1 和水平2 变量的跨水平交互作用,是重点考察的效应量指标。

3 置信区间宽度等高线图生成步骤

基于模拟的方法生成置信区间宽度等高线图实现样本量规划包含以下步骤。

第一, 设置参数。在实验研究背景下, 选用特定的LMEM, 设置水平1、水平2 样本量1当水平1、水平2 自变量为分类变量时, 可设定不同类别的样本量。, 固定效应取值, 以及随机效应分布。

第二, 生成数据。基于步骤一中定义的模型重复生成数据N次(如,N= 1000)。

第三, 参数估计。对于每次重复, 使用产生模型与数据拟合。应用R 软件包lme4(Bates et al.,2023)基于限制性极大似然(restricted maximum likelihood, REML)方法估计参数。采用默认的Wald方法计算效应量参数的CI。

第四, 变化水平1、水平2 样本量, 重复步骤一到三。

第六, 根据标准对评价指标作出判断, 画出CI宽度等高线图, 推荐合适的样本量。本研究建议采用效应量标准的最高水平减去最低水平作为可接受的最大CI 宽度。

本研究基于R 语言(R Development Core Team,2020)编写了适用于 LMEMs 样本量规划的函数samplesize_LMEM.R (见在线补充材料2)。调用函数, 并输入相应的参数运行程序, 可以得到评价指标结果和CI 宽度等高线图。应用流程如图1 所示。调用语句及其说明请参考在线补充材料3。本函数具有一定的灵活性, 例如设置ω002= 0时, 数据生成模型简化为不含刺激随机效应的模型; 设置ω002= 0,τ112= 0时, 简化为随机截距模型; 设置ω002= 0,τ112= 0,ICC= 0时, 简化为一般线性模型。

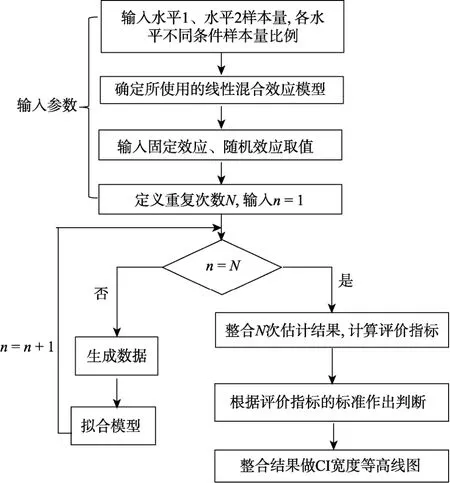
图1 CI 宽度等高线图生成流程图

调用线性混合效应模型样本量规划R 函数的语句见附图5。

附图5 调用线性混合效应模型进行样本量规划函数语句

如上图所示, 第1 行表示调用附件2 中的R 函数。第2 行输入模拟的重复次数。第3、4 行分别输入水平2 和水平1 样本量的向量, 假设长度分别为M 和P, 这些设定值完全交叉, 共形成M×P 种处理水平的组合。第5、6 行分别表示水平1 分类自变量两个水平样本量占总体的比例。第7、8 分别表示模型2 水平2 分类自变量两个水平样本量占总体的比例。第10 行表示CI 等高线图中的等高线刻度, 研究者可根据可接受的最宽CI 宽度结合实际情况自行定义。第12 行表示运行基于模型1 (水平1 自变量为2 个类别的分类变量)的模拟程序并输出结果, 括号内输入的参数在N 之后依次为γ10.std,γ00, ICC,τ11.std2,σ2,ω002。第15行表示运行基于模型2 且水平2 自变量为2 个类别的分类变量(水平1 自变量为2 个类别的分类变量)的模拟程序并输出结果, 括号内输入的参数在N 之后依次为表示水平2 自变量类型的指标变量(0 表示分类变量,1 表示连续变量),γ10.std,γ11.std,γ01.std,γ00, ICC,τ11.std2,σ2,ω002。第18 行表示运行基于模型2 且水平2 自变量为连续变量(水平1 自变量为2 个类别的分类变量)的模拟程序并输出结果, 括号内输入的参数与第15 行相同。第13、16 和19 行表示调用结果绘制CI 宽度等高线图。

研究者运行附图5 中的第1——10 行, 以及第12-13、15-16、18-19 任一行代码, 即可得到模拟生成的数据、真值、拟合结果、整合后的评价指标结果(模型1 为“modelOne_evaluation_accuracy.csv”, 模型2 为“modelTwo_evaluation_accuracy.csv”)和两种CI 宽度等高线图。注意, 如果有时得不到某种CI 等高线图, 可能是因为没有符合要求的样本量组合以形成图中的阴影区域。即, 对于检验力+CI 宽度等高线图, 在输入的水平1、水平2 样本量的所有组合下, 没有满足检验力大于等于0.8 的情况；对于检验力+随机效应估计准确性+CI 宽度等高线图, 在输入的水平1、水平2 样本量的所有组合下, 没有同时满足检验力大于等于0.8 并且所有随机效应估计值rbias 小于0.1 的情况。此时研究者可以检查评价指标结果文档进一步确认。

下面通过两个模拟研究, 考察不同因素对检验力和效应量估计准确性的影响, 说明CI (本研究为95% CI)宽度等高线图在样本量规划中的应用。

4 模拟研究1：基于被试内实验效应的样本量规划

研究1 在模型1 的框架下, 针对实验效应γ10,即水平1 自变量的固定效应, 考察γ10大小对模型估计结果的影响, 并通过CI 宽度等高线图提供样本量建议。

在H社区调查时，人力问题成为了我们调研期间的一个关键词，H社区负责人提到了基层编制不足，工作量大，给社区带来了巨大的压力。 根据公安部的标准，微型消防站人员配备应不少于六人。 微型消防站应设站长、副站长、消防员、控制室值班员等岗位，配有消防车辆的微型消防站应设驾驶员岗位。

4.1 参数设置

4.1.1 固定参数设置

基于模型 1 模拟生成数据。参照 Arend 和Schäfer (2019)的参数设置, 随机截距的固定效应γ00固定为0, 残差rij～N（ 0,1）。预研究发现, 组内相关2在多水平模型中, 组内相关ICC 用于表示零模型(不含任何预测变量的模型)中水平2 变异占总变异的比例, 值越大组间变异越大。一般而言, 被试嵌套于组的设计所得到的ICC 要小于测量嵌套于被试的ICC。(intraclass correlation coefficient, ICC)大小对γ10的检验力和参数估计准确性都没有显著影响,因此固定为中等水平0.3 (Arend & Schäfer, 2019),已知残差方差σ2= 1, 根据下式, 计算得到τ002的值。

标准化的随机斜率方差3预研究发现, 标准化的随机斜率方差 τ11.std2对 γ10的检验力和参数估计偏差影响不大。固定为中等水平(τ11.std2= 0.09)。为简化研究, 随机截距和随机斜率的协方差固定为 0 (ρ= 0, Arend & Schäfer,2019)。刺激的随机效应4本研究暂不考察刺激随机效应大小对样本量规划结果的影响,因此参考Cho 等(2017)的实证调查, 将刺激的随机效应固定为较小水平0.2。固定为较小水平ω002=0.2(Cho et al., 2017) 。最后, 根据残差方差, 得到用于产生数据的总体模型的随机斜率方差。

Xji设定为二分类变量(如, 控制组和实验组)。采用偏差编码(deviation coding, Barr et al., 2013;Lee, 2018)的形式, 编码为-0.5 和0.5。每种条件下重复模拟1000 次(例如Zhang, 2014)。

4.1.2 变化参数设置

参考Arend 和Schäfer (2019)的研究, 实验效应的大小(γ10.std5在多水平模型中, γ10. std=γ10*SDpredictor /SDoutcome。当自变量为分类变量时, γ10.std为部分标准化的回归系数, 即只对因变量标准化(SDo utcome =σ ,γ1 0.s td =γ10/σ)。该系数代表了自变量两个类别在因变量上的标准化均值差异(Cohen’s d)。。)设为3 个水平：0.2 (小)、0.5 (中)、0.8(大)。在每种条件下分别进行样本量规划。

水平1 样本量(J, 试次数), 包含10 个水平：10,20, 30, 50, 70, 100, 150, 200, 250, 300。水平2 样本量(I, 被试量), 包含9 个水平：10, 30, 50, 70, 100,200, 400, 600, 800。共形成10 × 9 = 90种样本量组合6水平1 样本量中, J = 10 的水平代表了Lee (2018)的研究中使用Laplace 接近方法没有收敛问题的条件, J = 300 的水平代表了Schultzberg 和Muthén (2018)关于动态结构方程模型样本量规划研究中测试时间点设置的最大水平。水平2 样本量中, I =10 的水平接近Lee (2018)总结的类似实验设计所使用的被试量最小值(16), I = 800 的水平接近Lee (2018)模拟研究中设置的1000 名被试的水平, 目的是为了探索大样本条件对效应量估计准确性提高的作用。最小到最大样本量水平之间的变化参考了同类样本量规划研究(例如Schultzberg & Muthén, 2018)。。

此外, 有研究证明, 当不同条件下试次数不等时(非平衡设计), 同等样本量条件下的检验力较小(Kumle et al., 2021)。因此, 为考察非平衡设计对样本量规划的影响, 在效应量中等的水平下, 增加自变量两个类别样本量不等的情况。参考Kumle 等(2021)的研究, 设两个水平的样本量比例为1 : 4。

综上, 完成参数设置, 调用samplesize_LMEM.R 函数运行得到结果。

4.2 评价指标

评价指标包括5 个方面。(1)收敛率。即参数估计收敛次数占总重复次数的比例。是否收敛采用lme4默认的Hessian 检验评价(Bates et al., 2023)。后面的所有评价指标均基于收敛的情况计算。(2)检验力。γ10的CI 不包括0 的次数占所有收敛次数的比例。预设的检验力标准为大于等于0.8。(3)效应量(固定效应)估计的准确性。包括估计偏差(bias),相对估计偏差(relative parameter estimation bias,rbias), 误差均方根(root mean squared error, RMSE),CI 宽度(width), CI 对真值的覆盖率(CP)。以γ10为例：

其中,γ10表示真值,N表示模拟重复次数。对于第n次重复,为γ10估计值,H(n)为估计结果是否收敛的指标变量,H(n)= 0 表示不收敛,H(n)= 1 表示收敛。width(n)表示的CI 宽度,coverage(n)为的CI是否覆盖真值γ10的指标变量,coverage(n)= 0表示没有覆盖真值,coverage（n）=1表示覆盖真值。如果效应量γ10估计准确, 则bias 应在0 附近, rbias 应小于其临界值0.1 (Koch et al.,2014), RMSE 应较小, width 应较窄, CP 应在0.925到0.975 之间(Bradley, 1978)。(4)效应量标准误估计的准确性。为评价效应量标准误估计的准确性, 计算了效应量的估计标准误相对于其估计值标准差的偏差(SE-SD bias)。以γ10为例,

4.3 研究结果

4.3.1 收敛情况

附表1 和2 (在线补充材料1)分别呈现了平衡和非平衡样本量分配条件下, 随机斜率模型(模型1)的收敛率。各条件下基本不存在收敛问题, 收敛率均在0.7 以上, 两个水平样本量均小于200 时,收敛率均超过0.9。另外, 效应量大小和是否为平衡设计对收敛率几乎没有影响。

附表1 研究一平衡设计各条件下线性混合效应模型收敛率

附表2 研究一非平衡设计各条件下线性混合效应模型收敛率

4.3.2 检验力结果

平衡设计各条件下检验力结果如表1 所示。从表中可以看出, 效应量越大, 检验力越大, 满足0.8标准需要的样本量越小。例如, 被试量为中等水平(200 人), 当效应量为0.2 时, 需要200 个试次才能保证检验力达到0.8 及以上; 而当效应量为0.8 时,只需要20 个试次就能保证检验力达到0.8 及以上。非平衡设计的检验力结果见附表3 (在线补充材料1)。对比发现, 非平衡设计的检验力普遍小于平衡设计的结果。例如, 当被试量为10 人, 检验力达到0.8 时, 平衡设计下需要50 个试次, 而非平衡设计下则需要100 个试次。

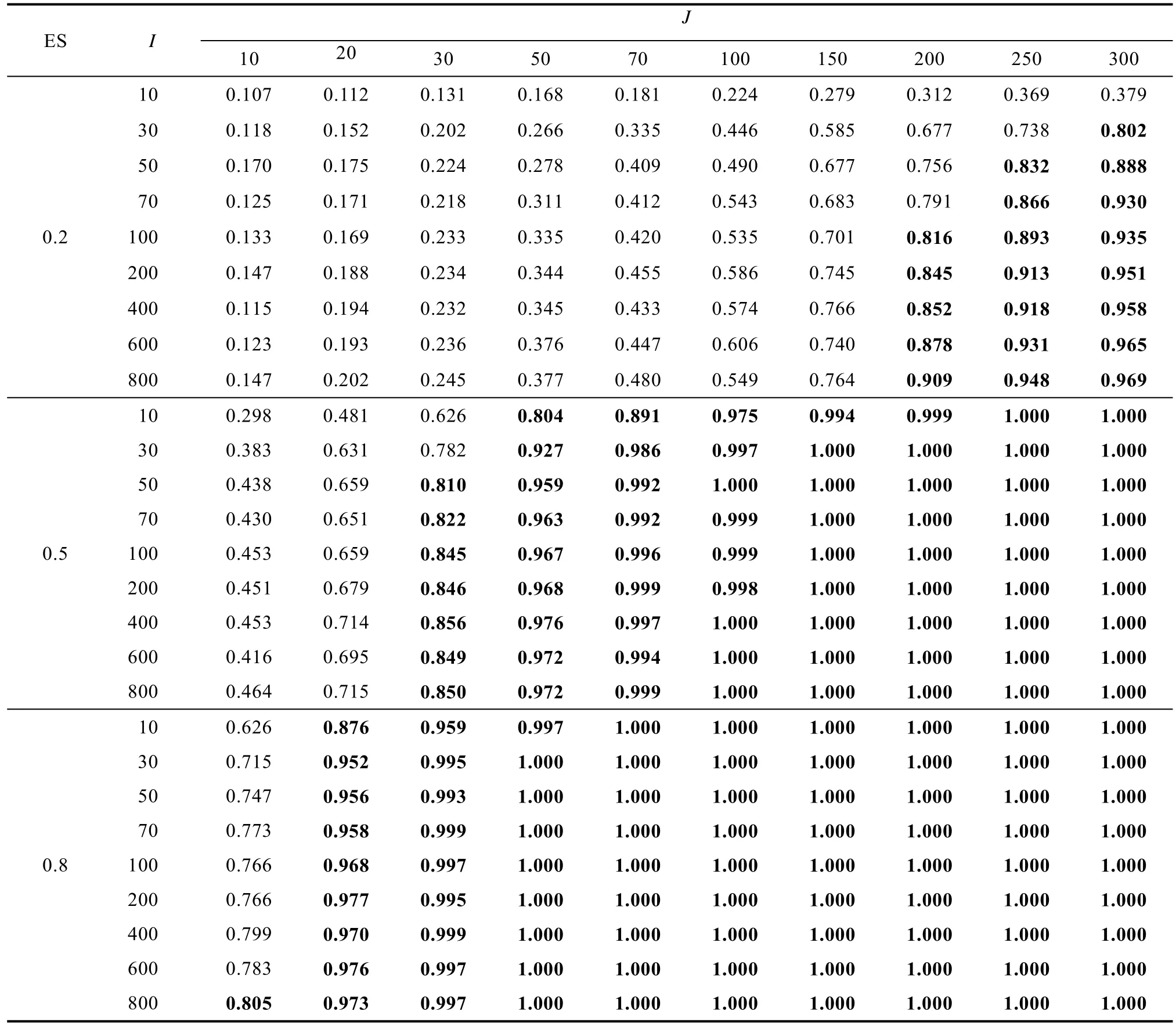
表1 研究1 平衡设计各条件下线性混合效应模型水平1 自变量效应的检验力

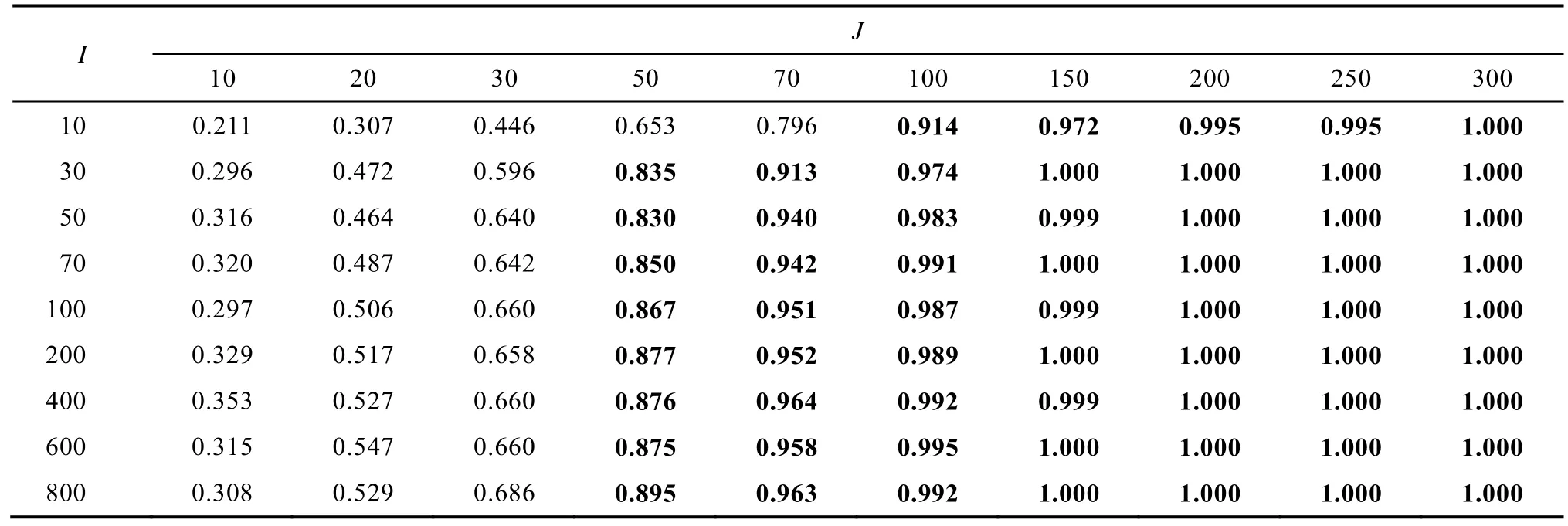
附表3 研究一非平衡设计效应量为0.5 时线性混合效应模型水平1 自变量效应的检验力

4.3.3 效应量及其标准误估计准确性结果

效应量大小对效应量及其标准误估计准确性结果没有显著影响。表2 呈现了平衡设计效应量为0.5 (中等)情况下效应量及其标准误估计准确性结果(只呈现rbias, width 和SE-SD bias 的结果, 其他评价指标结果见附表4, 效应量为0.2 和0.8 的结果见附表5、6, 在线补充材料1)。表2 结果显示所有条件下rbias 都小于0.1。此外, 附表4 显示在所有条件下, bias 都在0 附近波动; RMSE 较小, 基本在0.3 以下, 且随着水平1 和水平2 样本量增加, 尤其是水平1 样本量增加, RMSE 减小; 最后, 除了水平1 样本量为10 的条件外, 其他条件下的覆盖率都大于0.925。以上结果说明各条件下, 水平1 自变量的固定效应估计准确。

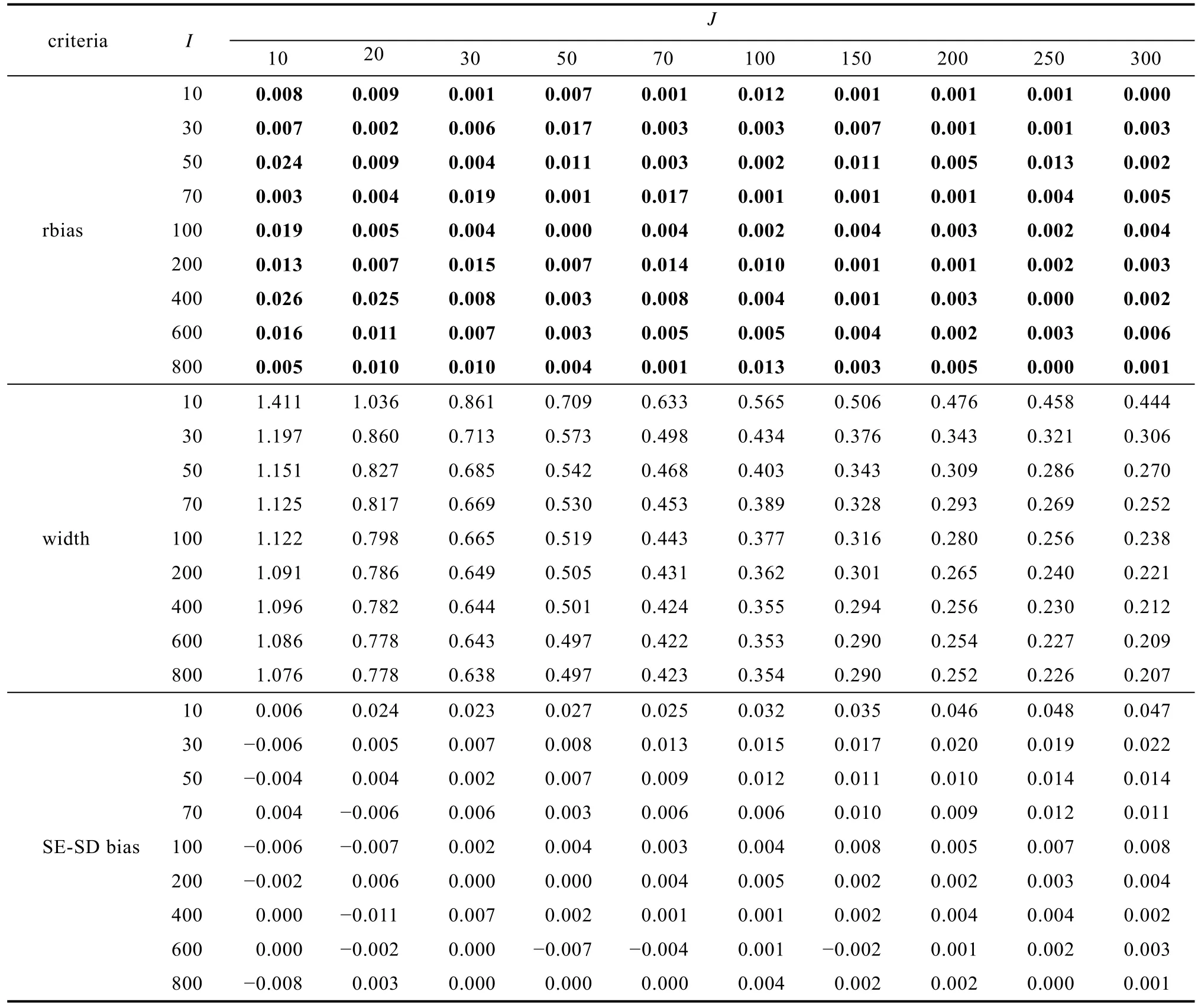
表2 研究1 平衡设计效应量为0.5 时水平1 自变量固定效应及其标准误估计准确性

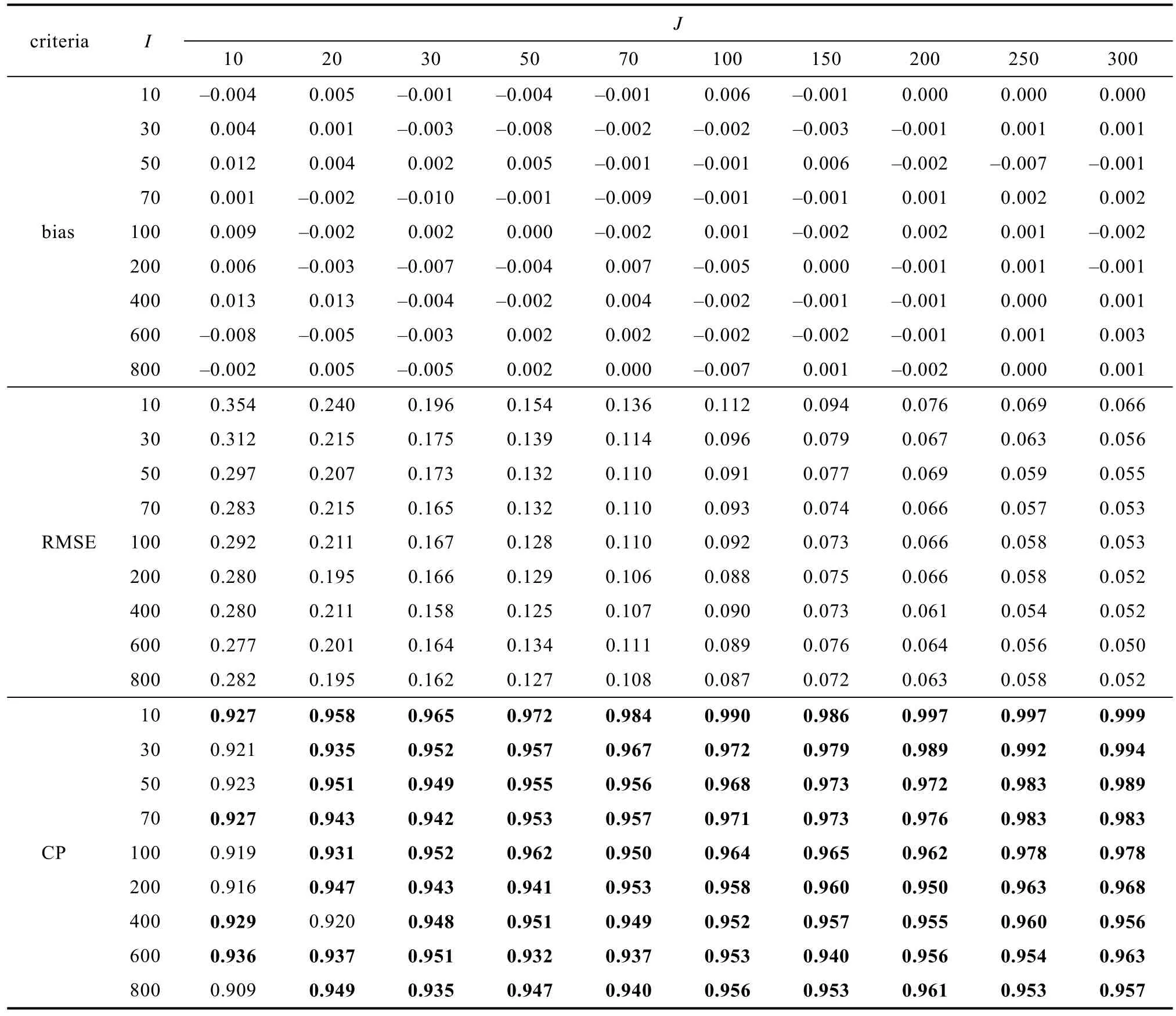
附表4 研究一平衡设计效应量为0.5 时线性混合效应模型水平1 自变量固定效应估计准确性

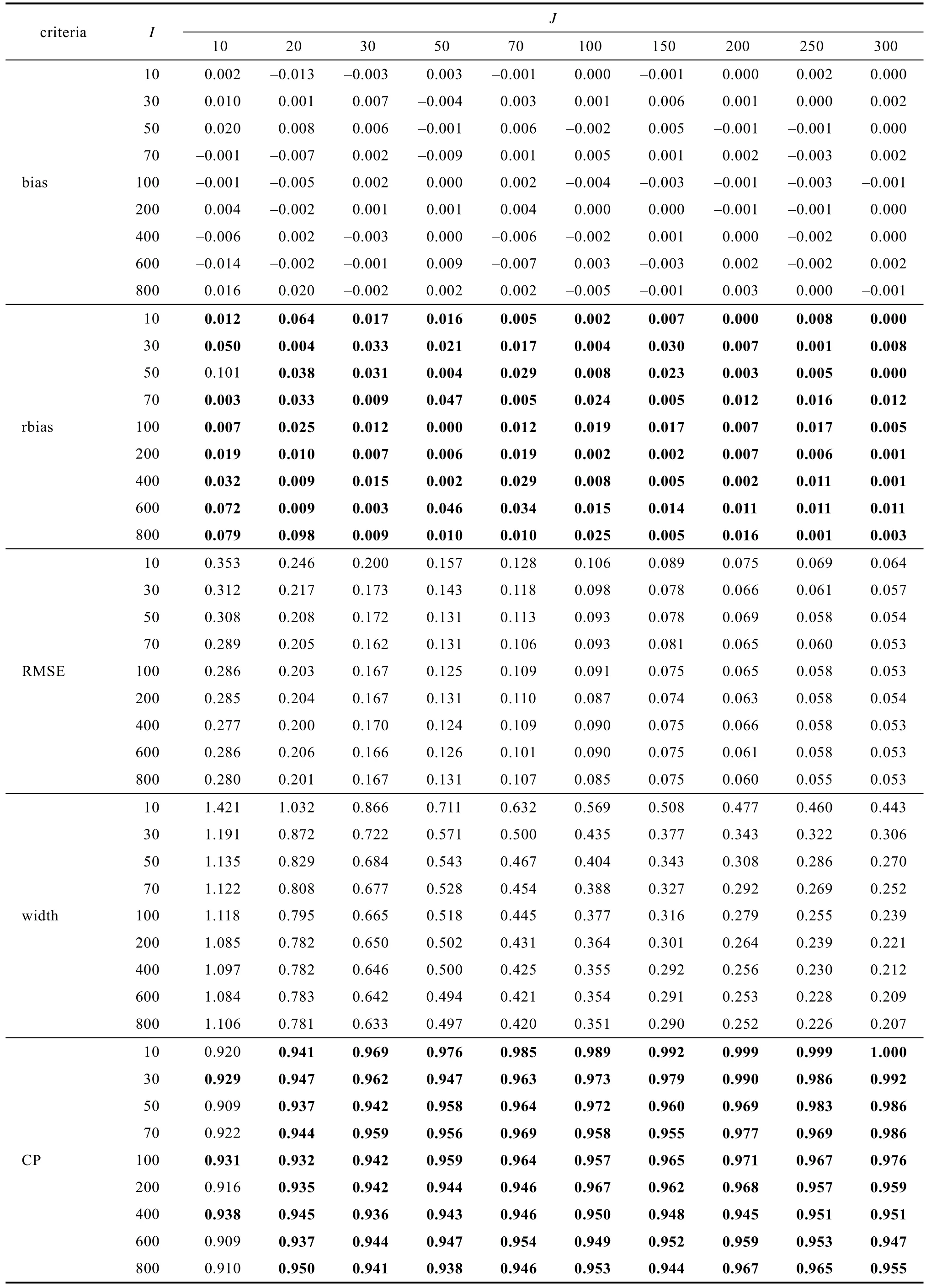
附表5 研究一平衡设计效应量为0.2 时线性混合效应模型水平1 自变量固定效应及其标准误估计准确性

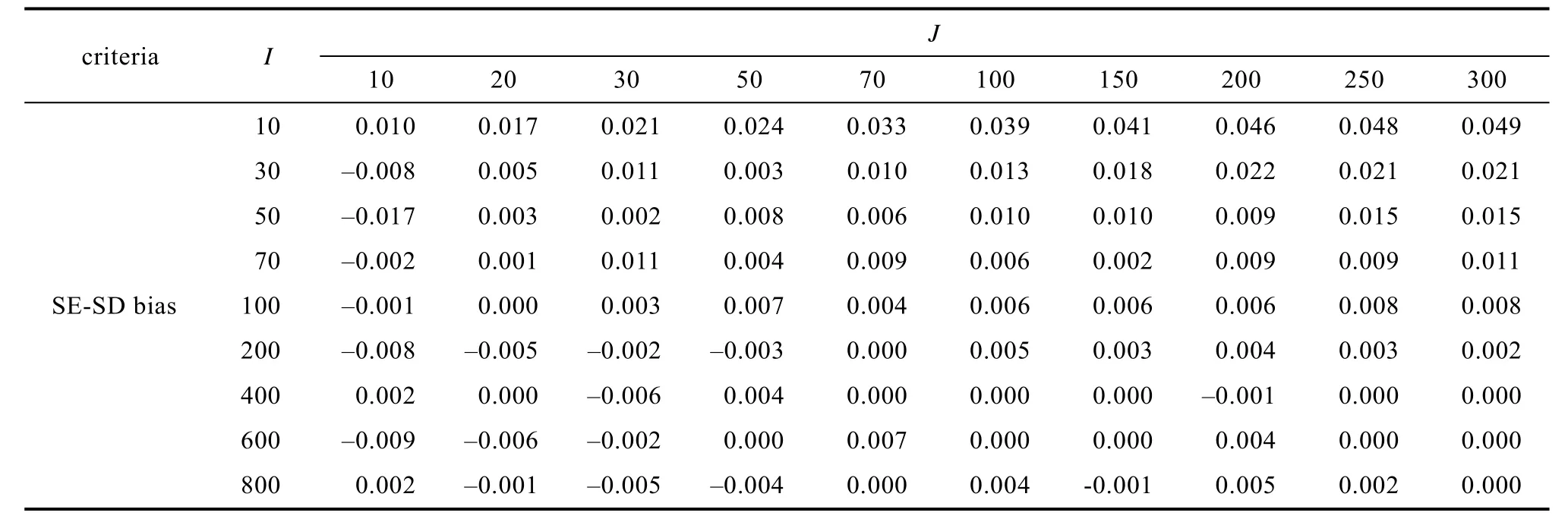
续附表5

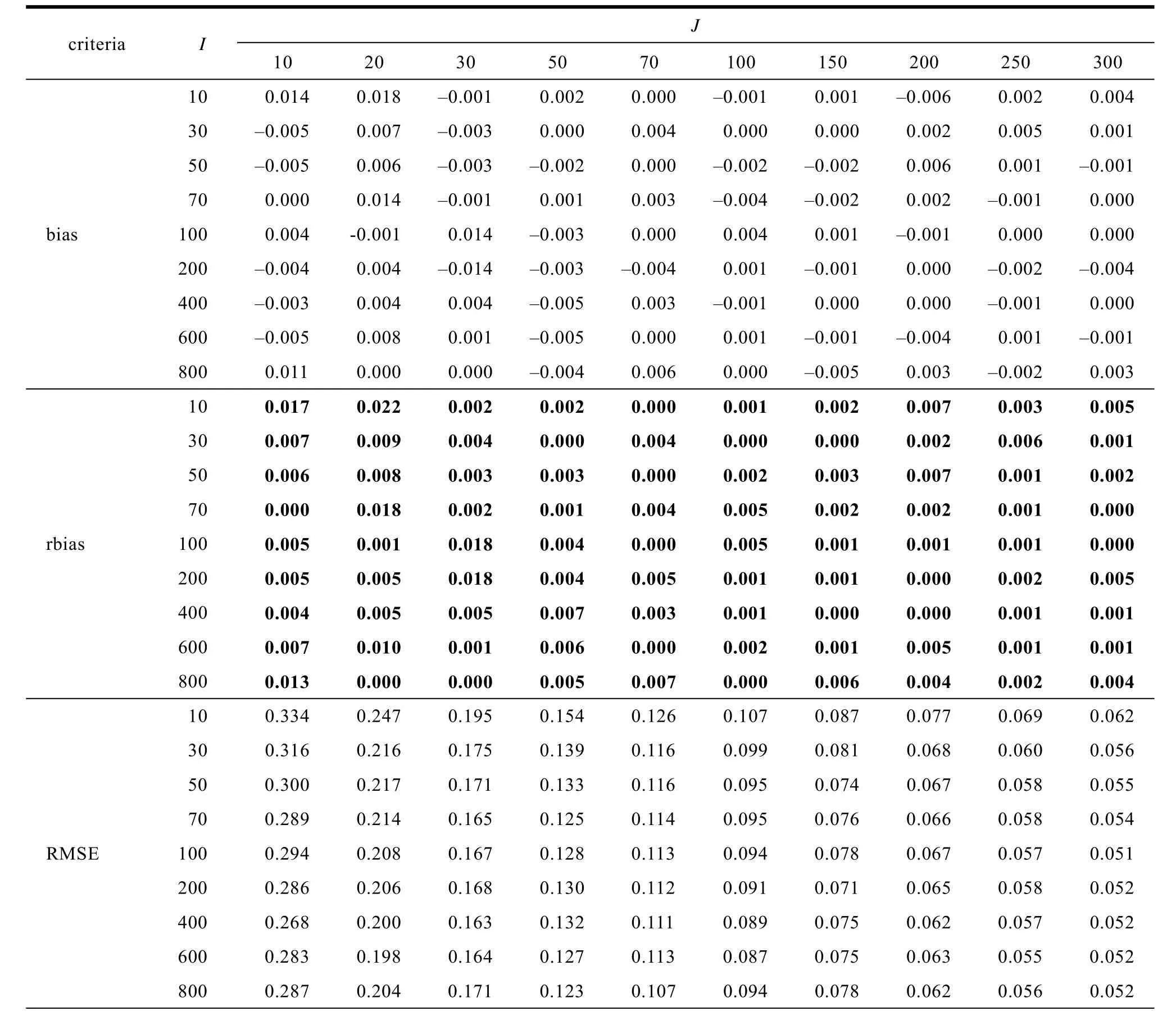
附表6 研究一平衡设计效应量为0.8 时线性混合效应模型水平1 自变量固定效应及其标准误估计准确性

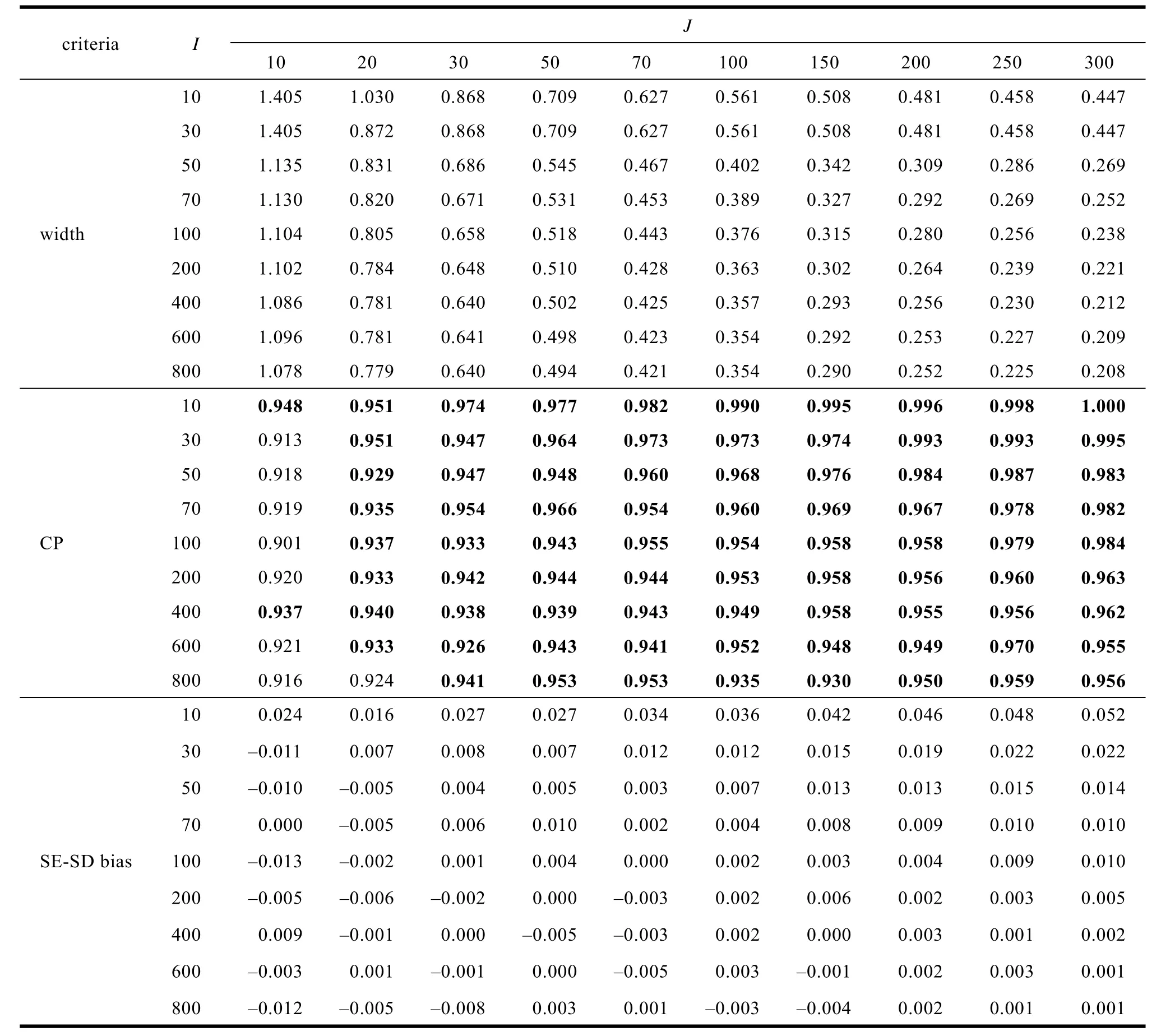
续附表6

根据效应量小和大的标准值0.2 和0.8, 定义可接受的最宽95% CI 宽度为0.8 - 0.2 = 0.6。从表3看出, 当水平1 样本量为30 及以下时, 95% CI 宽度均超过了0.6。说明在这些情况下效应量估计的标准误较大, 导致其95% CI 较宽。

最后, 各种条件下SE-SD bias 都在0 附近波动,说明效应量标准误估计较准确。

此外, 附表7 (在线补充材料1)呈现了非平衡设计下的固定效应及其标准误估计准确性结果。与平衡设计下的结果相比, 非平衡设计下的RMSE 更大, 95% CI 更宽。

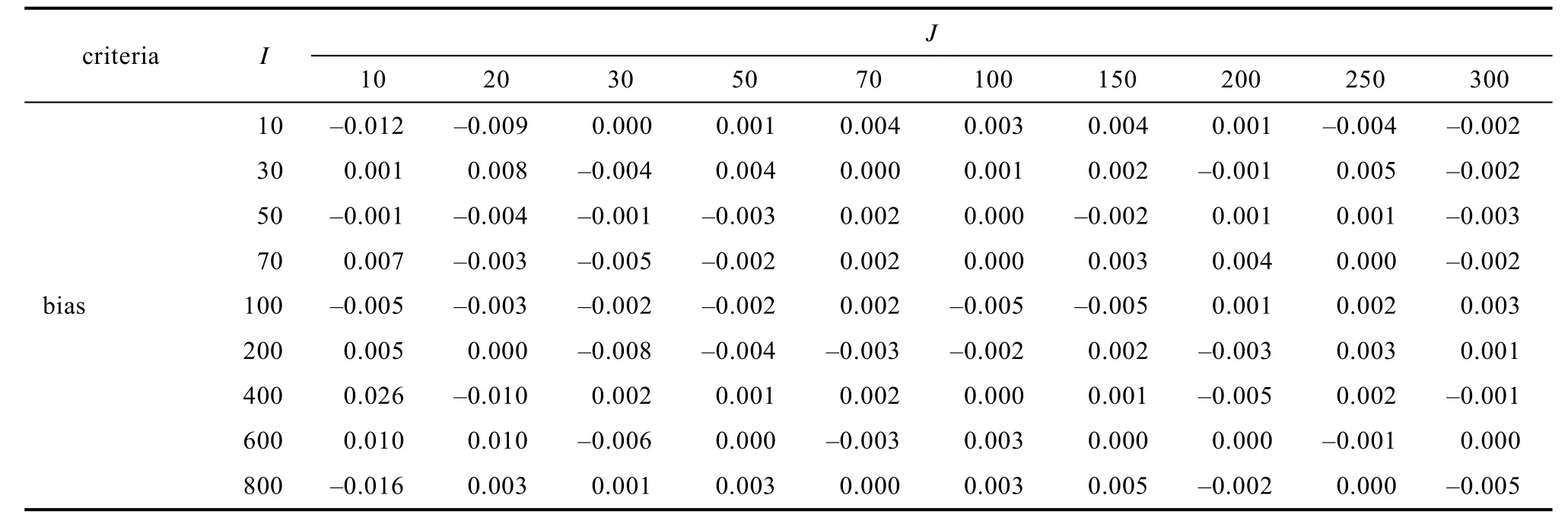
附表7 研究一非平衡设计效应量为0.5 时线性混合效应模型水平1 自变量固定效应及其标准误估计准确性

4.3.4 随机效应估计准确性结果

效应量大小基本不会影响随机效应估计准确性(附表8～11, 在线补充材料1)。从附表9 看出, 平衡设计水平1 自变量效应量为0.5 情况下,σ2估计值的rbias 均小于0.1,τ002的估计准确性略优于ω002,τ112的估计准确性相对最低。附表11 显示,与平衡设计下的结果相比, 非平衡设计下τ002和τ112的估计偏差更大。

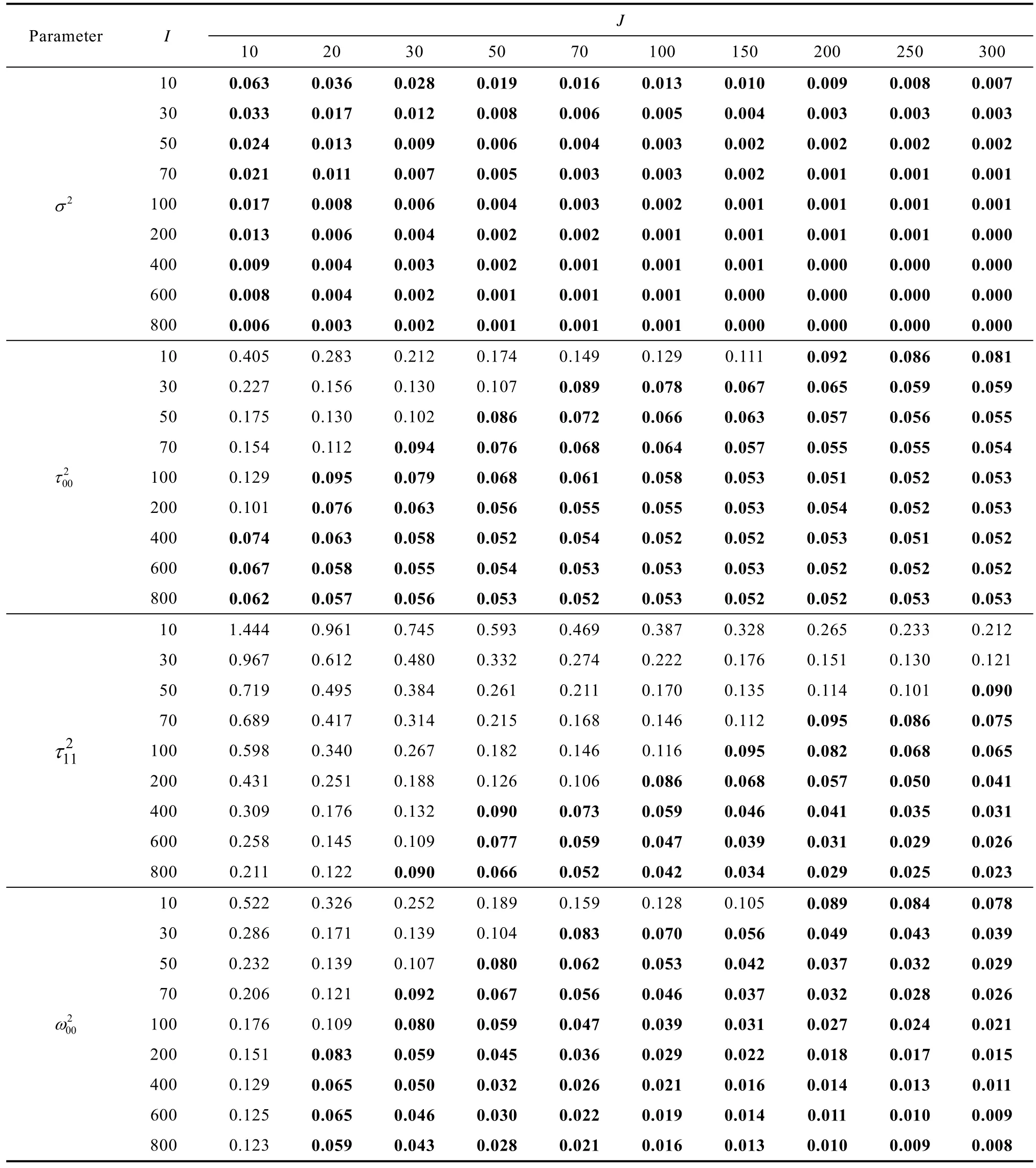
附表8 研究一平衡设计效应量为0.2 时线性混合效应模型随机效应估计rbias

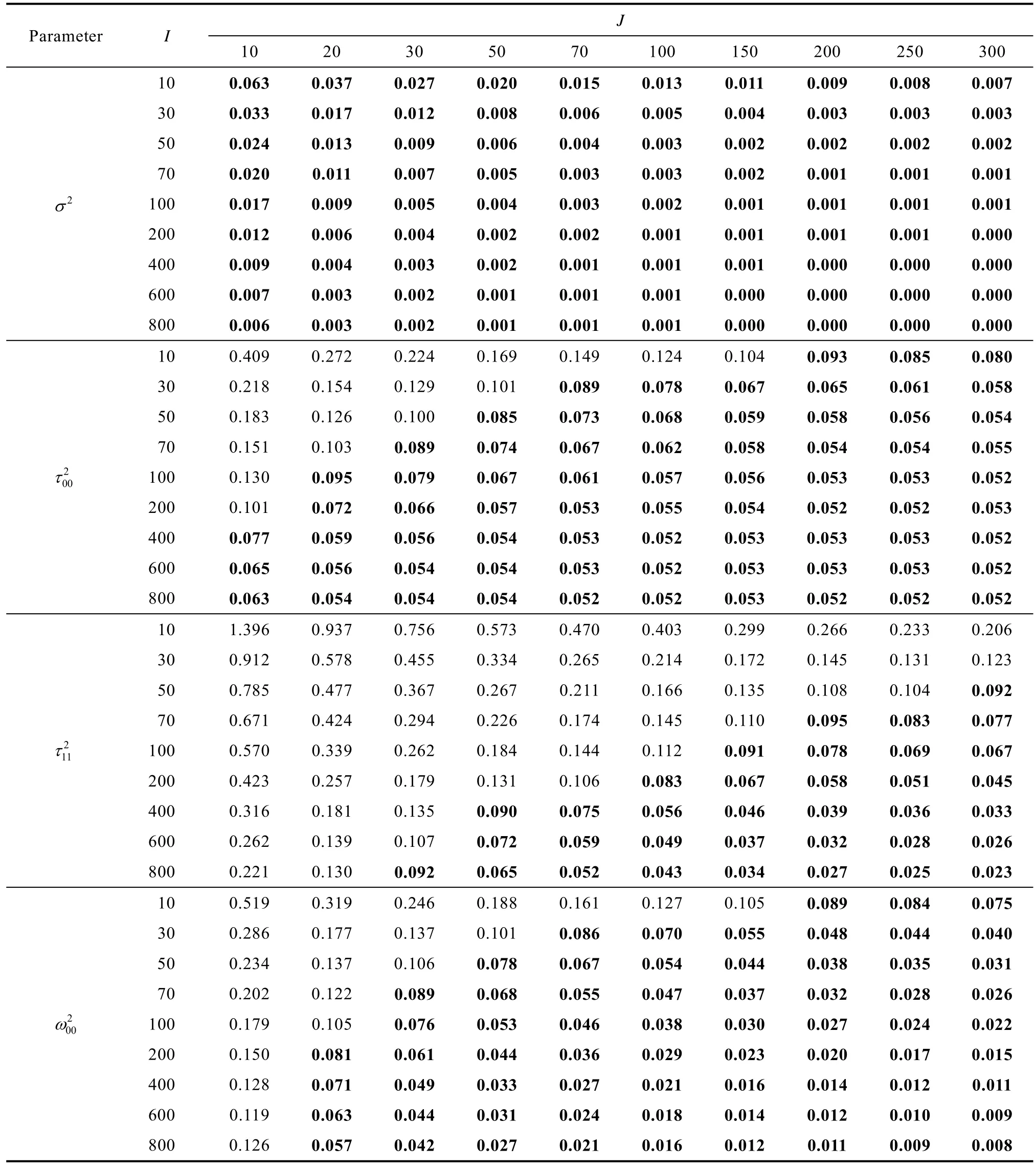
附表9 研究一平衡设计效应量为0.5 时线性混合效应模型随机效应估计rbias

附表10 研究一平衡设计效应量为0.8 时线性混合效应模型随机效应估计rbias

附表11 研究一非平衡设计效应量为0.5 时线性混合效应模型随机效应估计rbias

4.3.5 样本量规划建议

本研究提出了应用CI 宽度等高线图给出样本量规划建议。效应量准确性主要通过CI 宽度来反映。此外, 考虑到随机效应方差也可以作为效应量指标(Hox et al., 2017), 因此也可以同时结合检验力、随机效应方差估计准确性和CI 宽度来规划样本量。以水平1 自变量效应量为0.5 的情况为例, 图2(a)为检验力+CI 宽度等高线图, 阴影区域表示符合检验力大于等于0.8 标准的条件; 图2(b)为检验力+随机效应估计准确性+CI 宽度等高线图, 阴影区域表示符合检验力大于等于0.8 且所有随机效应估计值rbias 小于0.1 的条件。不同颜色对应于不同的CI 宽度。

图2 研究1 平衡设计水平1 自变量效应量中情况下的CI 宽度等高线图

从图2 可看出, 首先, 对于检验力, 或检验力+随机效应估计准确性, 两个水平样本量具有相互补偿的作用。但是, 当水平1 (试次)的样本量过小时(例如, 小于30), 无论怎样增加水平2 (被试)样本量, 也无法使得检验力或检验力+随机效应估计准确性达到要求。其次, 95% CI 宽度受水平1 样本量影响更大。当水平1 样本量较小时(如10), 即使增大水平2 样本量, 也很难减小95% CI 宽度。最后,与图a 相比, 图b 的阴影区域向右上移动, 说明增加考虑随机效应估计准确性的要求更加严格。水平1 自变量效应量为小、中和大情况下的等高线图见附图1～3 (在线补充材料1)。随着效应量增大, 阴影区域向下方移动, 满足要求的水平1 样本量减小。

附图1 研究一平衡设计水平1 自变量效应量小情况下的CI 宽度等高线图

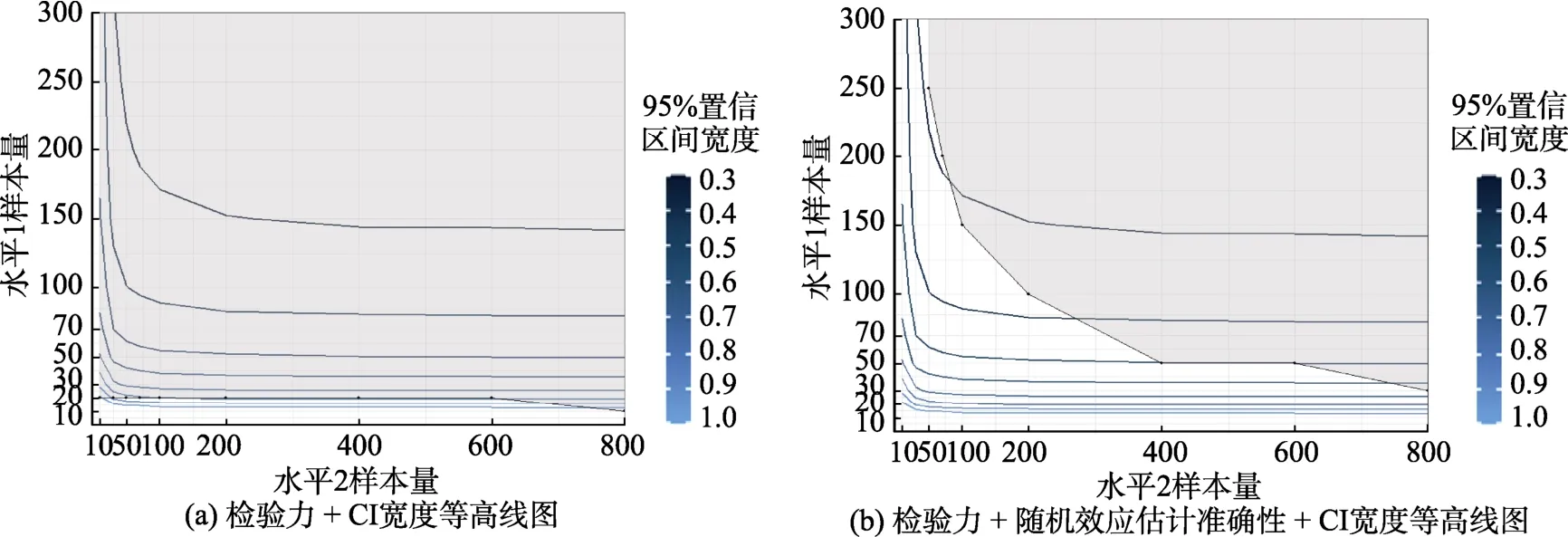
附图2 研究一平衡设计水平1 自变量效应量大情况下的CI 宽度等高线图

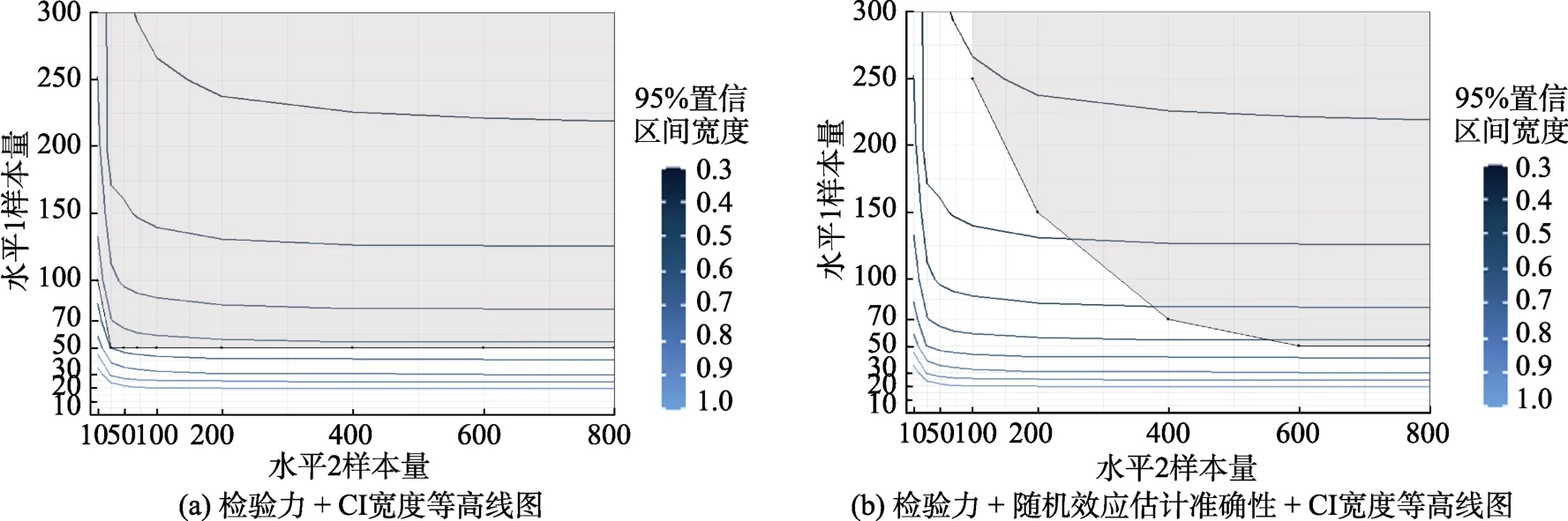
附图3 研究一非平衡设计水平1 自变量效应量中情况下的CI 宽度等高线图

应用CI 宽度等高线图时, 首先根据阴影区域找出符合要求(检验力大于等于0.8, 或检验力大于等于0.8 且所有随机效应估计值rbias 小于0.1)的范围。然后, 在阴影区域中, 通过与可接受的最宽CI宽度比较, 得到合适的样本量组合。例如, 根据图2, 满足检验力大于等于0.8 的标准, 95% CI 宽度小于等于0.6, 则推荐水平1 样本量 = 50, 水平2 样本量 = 30。满足检验力大于等于0.8 且所有随机效应估计值rbias 小于0.1, 95% CI 宽度小于等于0.6,则推荐水平1 样本量 = 50, 水平2 样本量 = 400。

从附图3 看出, 与平衡设计相比, 非平衡设计下的阴影区域向上方移动, 满足要求的水平1 样本量增大, 至少为50 才能保证检验力符合要求。

5 模拟研究2：基于被试变量调节效应的样本量规划研究

研究2 在模型2 的框架下, 针对被试变量的调节效应(γ11, 跨水平交互作用), 考察τ211大小和被试变量类型对模型估计结果的影响, 并通过CI 宽度等高线图提供样本量建议。

5.1 参数设置

5.1.1 固定参数设置

考虑到实际中被试变量iW可能为分类变量(如,性别)或连续变量(如, 情绪唤醒度), 研究2 分为两种情境：情境1 中,iW为二分变量, 采用偏差编码(-0.5 和0.5); 情境2 中,iW为连续变量, 服从标准正态分布。

与研究1 类似, 随机截距的固定效应γ00固定为0。研究2 主要关注γ11, 因此, 将Xji和Wi的主效应固定为中等水平, 即：γ10.std=0.5,γ01.std=0.5(情境1),γ01.std= 0.3(情境2)。为简化研究, 参考检验力分析研究的普遍设计(例如Arend & Schäfer,2019), 将γ11.std也固定为中等水平, 即：γ11.std=0.5(情境1),γ11.std=0.3(情境2)(Cohen,1988)。

与研究1类似,残差方差设定为σ2= 1。情境1中, 在τ11.std2= 0.01 (小), 0.09 (中)和0.25 (大)三种水平下(Arend & Schäfer, 2019), 根据公式(14), 可得到三种水平下的τ112=0.01, 0.09 和0.25。

利用τ11对标准化的跨水平交互效应进行调整,得到用于产生数据的总体模型的固定效应参数(Arend & Schäfer, 2019)7在多水平模型中, γ1 1 . s td =γ11 * SD p redictor /SDoutcome。当 Wi 为分类变量时, γ11.std为部分标准化的回归系数, 即只对因变量标准化( SDo utcome = τ11 , γ1 1 . s td=γ11 /τ11; 当 Wi 为连续变量时, 由于自变量已经标准化( SD p redictor = 1), 则 γ1 1 .s td=γ11/τ11为完全标准化的回归系数。。

因此, 在情境1 中, 随机斜率方差的三种水平下γ11= 0.05, 0.15 和0.25; 在情境2 中, 固定τ11.std2为中等水平(0.09), 可得到γ11= 0.09。γ11表示被试变量对实验效应的调节效应。在情境1 中,γ11表示Wi=- 0.5的被试和Wi= 0.5的被试在两个实验水平上结果差异的差异。在情境2 中,γ11表示Wi越高/越低的被试, 在两个实验水平上结果的差异越大/越小。ICC 固定为中等水平。ω002固定为0.2。每种条件下数据重复模拟N= 1000 次。

5.1.2 变化参数设置

情境1 中, 在τ11.std2分别为0.01, 0.09 和0.25(公式(14))时分别进行样本量规划。同时, 为考察非平衡设计对样本量规划的影响, 增加被试变量两个类别样本量不等的情况(1 : 4)。样本量设置与研究1相同。调用samplesize_LMEM.R 函数运行得到结果。

5.2 评价指标

与研究1 相同。

5.3 研究结果

5.3.1 收敛情况

研究2 中LMEMs 的收敛率见附表12、13 (在线补充材料1)。可以看出, 当τ112小,Wi为分类变量时, 在部分条件下, 收敛率低于0.7。甚至在有些条件下(I= 800,J= 250 或300), 仅有不到一半的重复收敛。说明当较小时, 采用随机斜率模型可能会带来不收敛的问题。其余各条件下基本不存在收敛问题, 收敛率普遍在0.7 以上。Wi为分类变量或连续变量、是否为平衡设计对收敛率几乎没有影响。

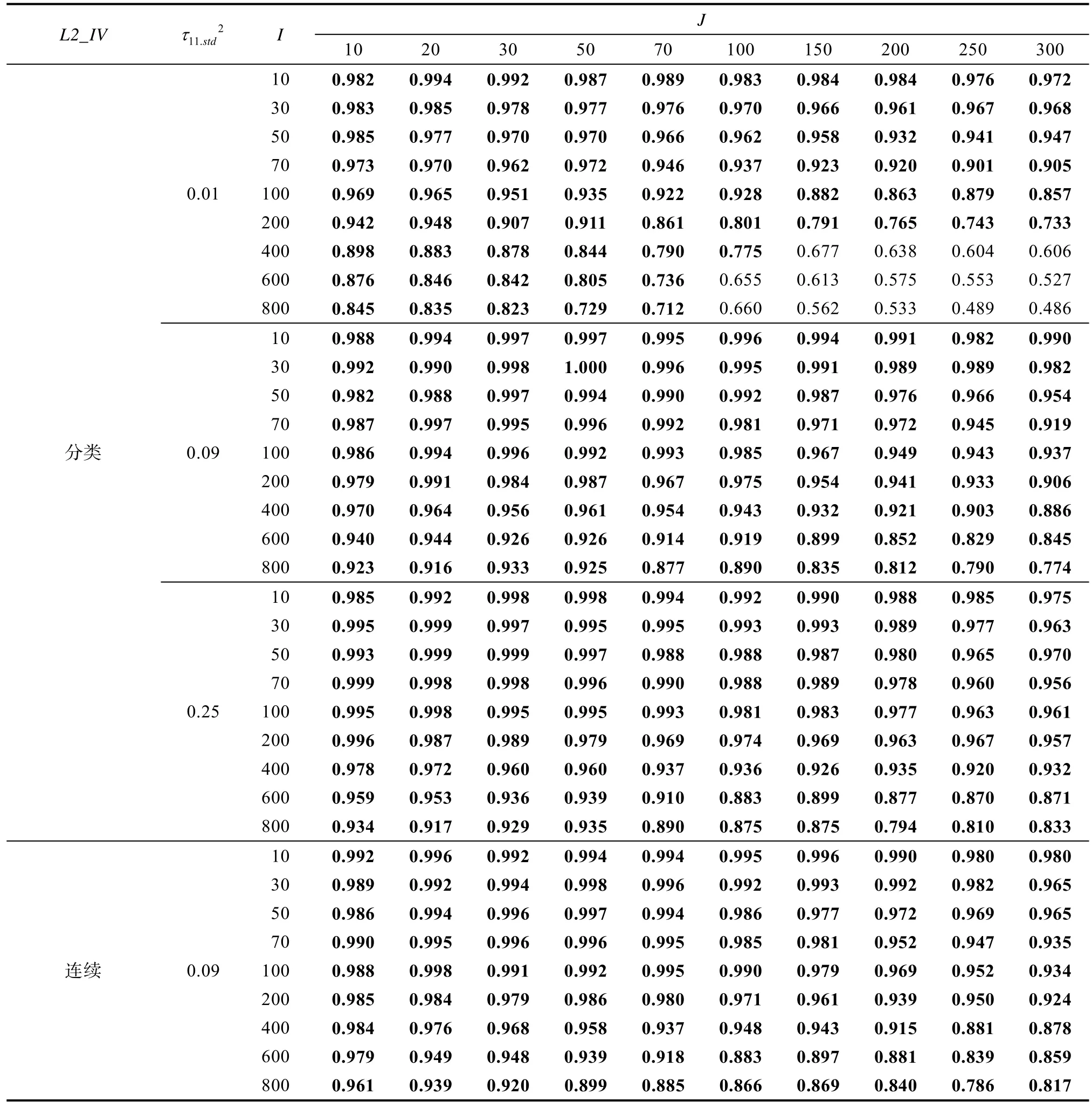
附表12 研究二平衡设计各条件下线性混合效应模型收敛率

附表13 研究二非平衡设计为中等时线性混合效应模型收敛率

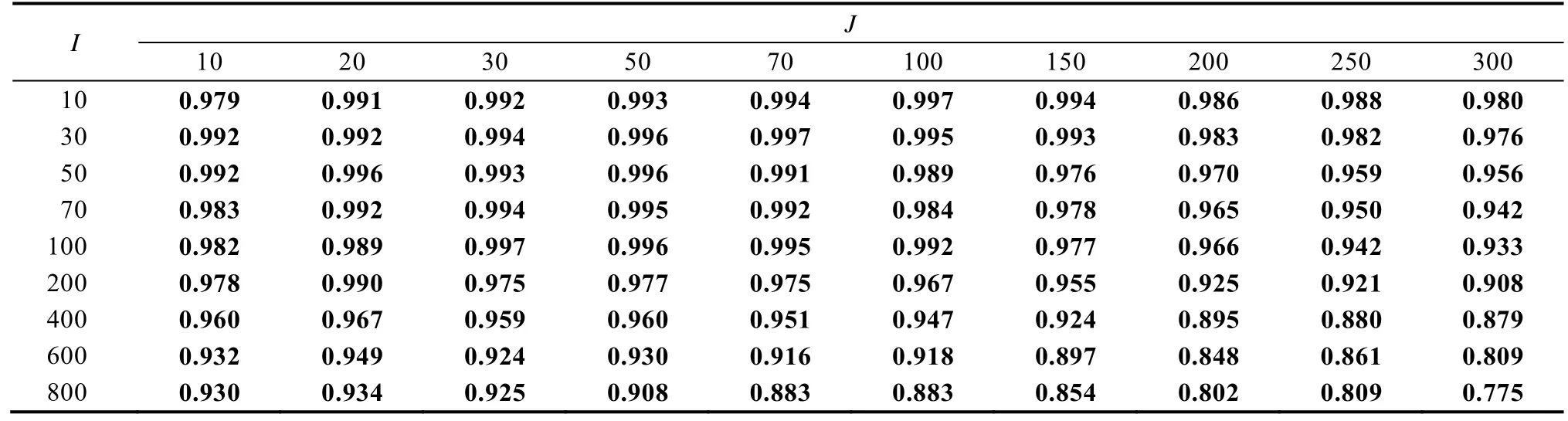
附表13 研究二非平衡设计为中等时线性混合效应模型收敛率

注：J 表示水平1 样本量，I 表示水平2 样本量。表中加粗的为收敛率大于等于0.7 的结果。

I J 10 20 30 50 70 100 150 200 250 300 10 0.979 0.991 0.992 0.993 0.994 0.997 0.994 0.986 0.988 0.980 30 0.992 0.992 0.994 0.996 0.997 0.995 0.993 0.983 0.982 0.976 50 0.992 0.996 0.993 0.996 0.991 0.989 0.976 0.970 0.959 0.956 70 0.983 0.992 0.994 0.995 0.992 0.984 0.978 0.965 0.950 0.942 100 0.982 0.989 0.997 0.996 0.995 0.992 0.977 0.966 0.942 0.933 200 0.978 0.990 0.975 0.977 0.975 0.967 0.955 0.925 0.921 0.908 400 0.960 0.967 0.959 0.960 0.951 0.947 0.924 0.895 0.880 0.879 600 0.932 0.949 0.924 0.930 0.916 0.918 0.897 0.848 0.861 0.809 800 0.930 0.934 0.925 0.908 0.883 0.883 0.854 0.802 0.809 0.775

5.3.2 检验力结果

各条件下γ11检验力结果如附表14、15 (在线补充材料1)所示。可以看出,越大, 检验力越大。Wi为连续变量得到的检验力普遍大于Wi为分类变量的情况, 这可能与连续变量提供的信息量更多有关。随着两个水平样本量增加, 尤其是水平2 样本量增加, 检验力增加。与研究1 不同, 研究2 中的检验力受水平2 样本量影响更大, 这是因为研究2中的检验力是针对水平2 自变量计算的, 受被试量影响更大, 而研究1 中的检验力针对水平1 自变量计算, 受试次数影响更大。此外, 非平衡设计的检验力普遍小于平衡设计的结果。

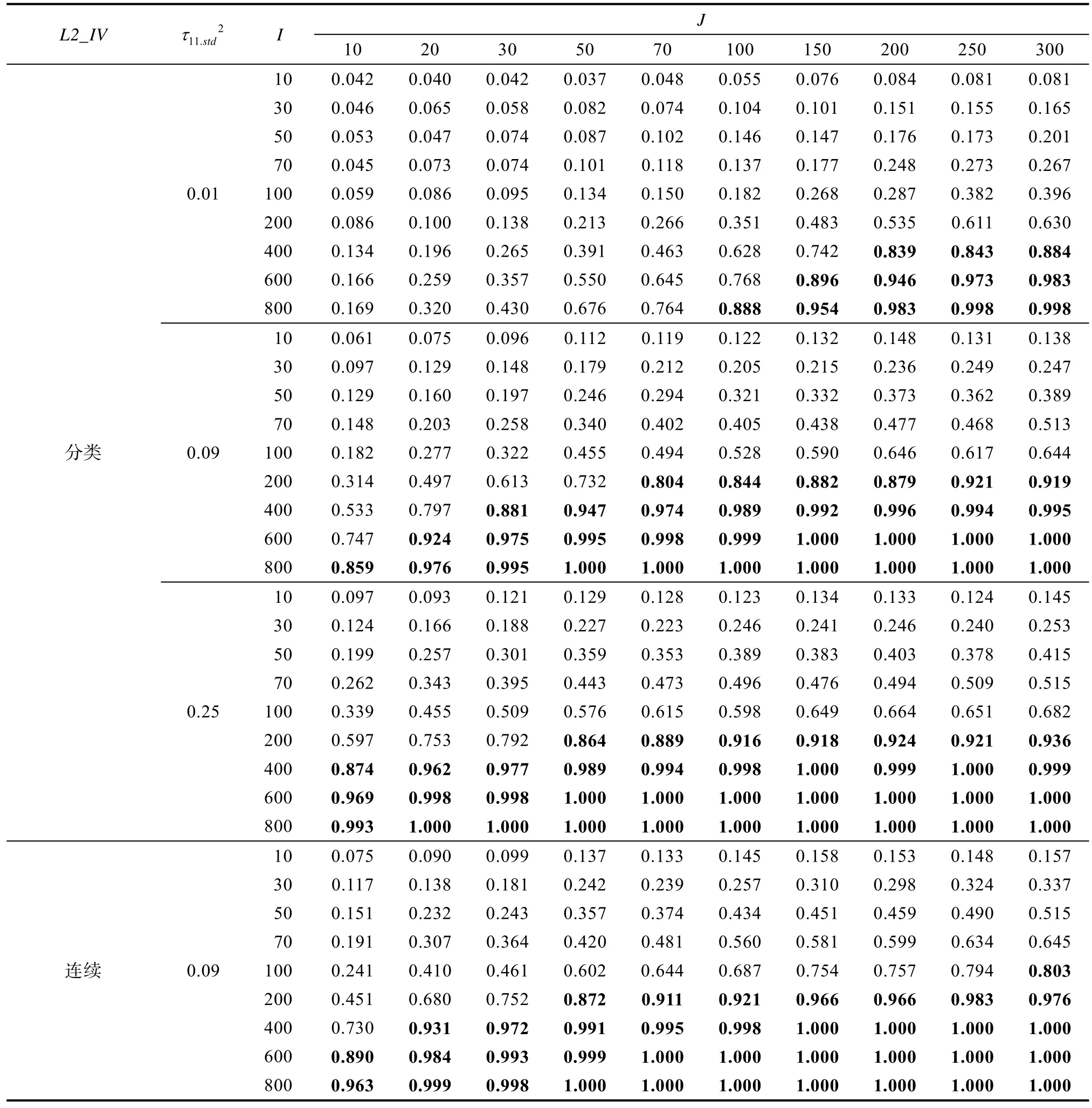
附表14 研究二平衡设计各条件下线性混合效应模型水平2 自变量调节效应的检验力

附表15 研究二非平衡设计为中等时线性混合效应模型水平2 自变量调节效应的检验力

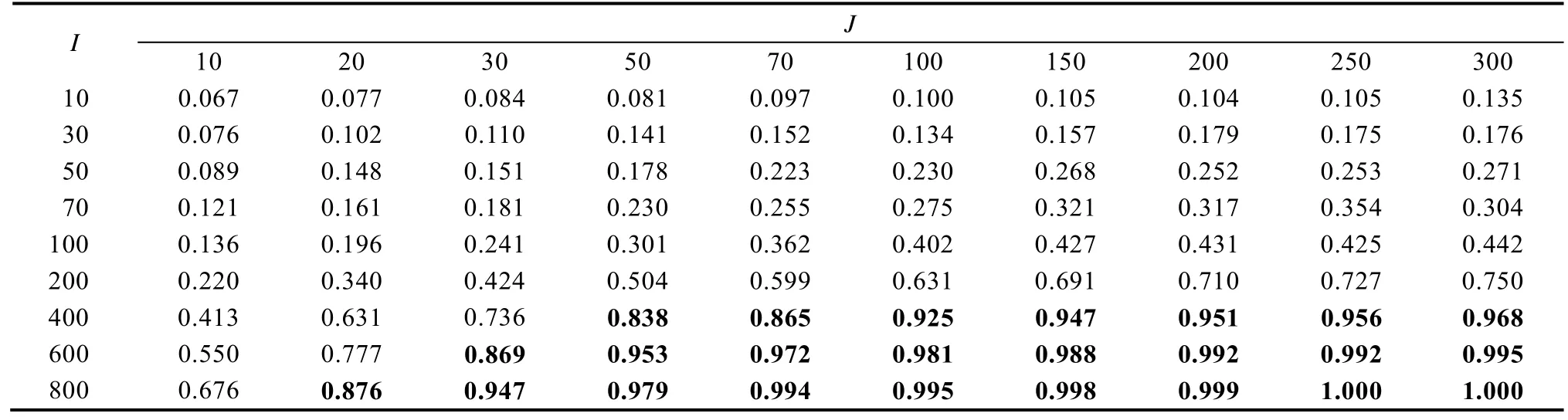
附表15 研究二非平衡设计为中等时线性混合效应模型水平2 自变量调节效应的检验力

注：J 表示水平1 样本量，I 表示水平2 样本量。表中加粗的为检验力大于等于0.8 的结果。

I J 10 20 30 50 70 100 150 200 250 300 10 0.067 0.077 0.084 0.081 0.097 0.100 0.105 0.104 0.105 0.135 30 0.076 0.102 0.110 0.141 0.152 0.134 0.157 0.179 0.175 0.176 50 0.089 0.148 0.151 0.178 0.223 0.230 0.268 0.252 0.253 0.271 70 0.121 0.161 0.181 0.230 0.255 0.275 0.321 0.317 0.354 0.304 100 0.136 0.196 0.241 0.301 0.362 0.402 0.427 0.431 0.425 0.442 200 0.220 0.340 0.424 0.504 0.599 0.631 0.691 0.710 0.727 0.750 400 0.413 0.631 0.736 0.838 0.865 0.925 0.947 0.951 0.956 0.968 600 0.550 0.777 0.869 0.953 0.972 0.981 0.988 0.992 0.992 0.995 800 0.676 0.876 0.947 0.979 0.994 0.995 0.998 0.999 1.000 1.000

5.3.3 效应量及其标准误估计准确性结果

调节效应量及其标准误估计准确性结果见附表16～20 (在线补充材料1)。可以看出,不同的条件下, bias, rbias, 95%CP 和SE-SD bias 的结果非常一致, 都较小。随着增加, RMSE 增大, 95% CI变宽。

附表16 研究二平衡设计小且 W i 为分类变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

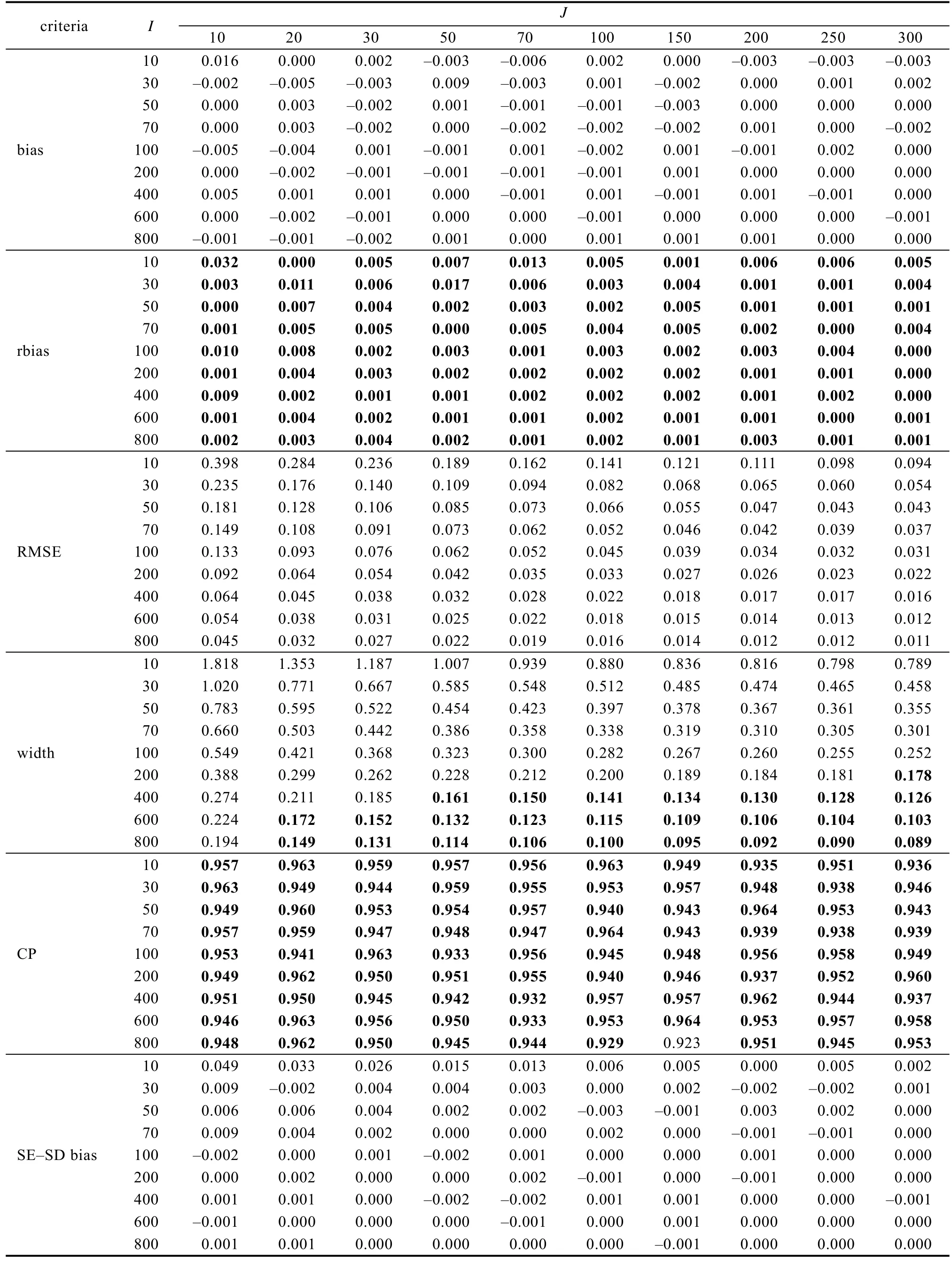
附表16 研究二平衡设计小且 W i 为分类变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

注：J 表示水平1 样本量，I 表示水平2 样本量，criteria 表示各评价指标。rbias 中加粗的为其值小于0.1 的结果，width 中加粗的为其值小于0.06 的结果，CP 中加粗的为其值大于0.925 的结果。

criteria I J 10 20 30 50 70 100 150 200 250 300 10 0.016 0.000 0.002 -0.003 -0.006 0.002 0.000 -0.003 -0.003 -0.003 bias 30 -0.002 -0.005 -0.003 0.009 -0.003 0.001 -0.002 0.000 0.001 0.002 50 0.000 0.003 -0.002 0.001 -0.001 -0.001 -0.003 0.000 0.000 0.000 70 0.000 0.003 -0.002 0.000 -0.002 -0.002 -0.002 0.001 0.000 -0.002 100 -0.005 -0.004 0.001 -0.001 0.001 -0.002 0.001 -0.001 0.002 0.000 200 0.000 -0.002 -0.001 -0.001 -0.001 -0.001 0.001 0.000 0.000 0.000 400 0.005 0.001 0.001 0.000 -0.001 0.001 -0.001 0.001 -0.001 0.000 600 0.000 -0.002 -0.001 0.000 0.000 -0.001 0.000 0.000 0.000 -0.001 800 -0.001 -0.001 -0.002 0.001 0.000 0.001 0.001 0.001 0.000 0.000 10 0.032 0.000 0.005 0.007 0.013 0.005 0.001 0.006 0.006 0.005 rbias 30 0.003 0.011 0.006 0.017 0.006 0.003 0.004 0.001 0.001 0.004 50 0.000 0.007 0.004 0.002 0.003 0.002 0.005 0.001 0.001 0.001 70 0.001 0.005 0.005 0.000 0.005 0.004 0.005 0.002 0.000 0.004 100 0.010 0.008 0.002 0.003 0.001 0.003 0.002 0.003 0.004 0.000 200 0.001 0.004 0.003 0.002 0.002 0.002 0.002 0.001 0.001 0.000 400 0.009 0.002 0.001 0.001 0.002 0.002 0.002 0.001 0.002 0.000 600 0.001 0.004 0.002 0.001 0.001 0.002 0.001 0.001 0.000 0.001 800 0.002 0.003 0.004 0.002 0.001 0.002 0.001 0.003 0.001 0.001 10 0.398 0.284 0.236 0.189 0.162 0.141 0.121 0.111 0.098 0.094 RMSE 30 0.235 0.176 0.140 0.109 0.094 0.082 0.068 0.065 0.060 0.054 50 0.181 0.128 0.106 0.085 0.073 0.066 0.055 0.047 0.043 0.043 70 0.149 0.108 0.091 0.073 0.062 0.052 0.046 0.042 0.039 0.037 100 0.133 0.093 0.076 0.062 0.052 0.045 0.039 0.034 0.032 0.031 200 0.092 0.064 0.054 0.042 0.035 0.033 0.027 0.026 0.023 0.022 400 0.064 0.045 0.038 0.032 0.028 0.022 0.018 0.017 0.017 0.016 600 0.054 0.038 0.031 0.025 0.022 0.018 0.015 0.014 0.013 0.012 800 0.045 0.032 0.027 0.022 0.019 0.016 0.014 0.012 0.012 0.011 10 1.818 1.353 1.187 1.007 0.939 0.880 0.836 0.816 0.798 0.789 width 30 1.020 0.771 0.667 0.585 0.548 0.512 0.485 0.474 0.465 0.458 50 0.783 0.595 0.522 0.454 0.423 0.397 0.378 0.367 0.361 0.355 70 0.660 0.503 0.442 0.386 0.358 0.338 0.319 0.310 0.305 0.301 100 0.549 0.421 0.368 0.323 0.300 0.282 0.267 0.260 0.255 0.252 200 0.388 0.299 0.262 0.228 0.212 0.200 0.189 0.184 0.181 0.178 400 0.274 0.211 0.185 0.161 0.150 0.141 0.134 0.130 0.128 0.126 600 0.224 0.172 0.152 0.132 0.123 0.115 0.109 0.106 0.104 0.103 800 0.194 0.149 0.131 0.114 0.106 0.100 0.095 0.092 0.090 0.089 10 0.957 0.963 0.959 0.957 0.956 0.963 0.949 0.935 0.951 0.936 CP 30 0.963 0.949 0.944 0.959 0.955 0.953 0.957 0.948 0.938 0.946 50 0.949 0.960 0.953 0.954 0.957 0.940 0.943 0.964 0.953 0.943 70 0.957 0.959 0.947 0.948 0.947 0.964 0.943 0.939 0.938 0.939 100 0.953 0.941 0.963 0.933 0.956 0.945 0.948 0.956 0.958 0.949 200 0.949 0.962 0.950 0.951 0.955 0.940 0.946 0.937 0.952 0.960 400 0.951 0.950 0.945 0.942 0.932 0.957 0.957 0.962 0.944 0.937 600 0.946 0.963 0.956 0.950 0.933 0.953 0.964 0.953 0.957 0.958 800 0.948 0.962 0.950 0.945 0.944 0.929 0.923 0.951 0.945 0.953 10 0.049 0.033 0.026 0.015 0.013 0.006 0.005 0.000 0.005 0.002 SE-SD bias 30 0.009 -0.002 0.004 0.004 0.003 0.000 0.002 -0.002 -0.002 0.001 50 0.006 0.006 0.004 0.002 0.002 -0.003 -0.001 0.003 0.002 0.000 70 0.009 0.004 0.002 0.000 0.000 0.002 0.000 -0.001 -0.001 0.000 100 -0.002 0.000 0.001 -0.002 0.001 0.000 0.000 0.001 0.000 0.000 200 0.000 0.002 0.000 0.000 0.002 -0.001 0.000 -0.001 0.000 0.000 400 0.001 0.001 0.000 -0.002 -0.002 0.001 0.001 0.000 0.000 -0.001 600 -0.001 0.000 0.000 0.000 -0.001 0.000 0.001 0.000 0.000 0.000 800 0.001 0.001 0.000 0.000 0.000 0.000 -0.001 0.000 0.000 0.000

附表17 研究二平衡设计中且 W i为分类变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

注：J 表示水平1 样本量，I 表示水平2 样本量，criteria 表示各评价指标。rbias 中加粗的为其值小于0.1 的结果，width 中加粗的为其值小于0.18 的结果，CP 中加粗的为其值大于0.925 的结果。

criteria I J 10 20 30 50 70 100 150 200 250 300 10 0.014 -0.012 0.001 0.001 -0.015 -0.012 -0.015 -0.010 -0.010 -0.008 bias 30 -0.002 0.001 -0.002 -0.003 0.005 -0.002 -0.007 0.001 0.003 -0.002 50 -0.005 0.000 -0.003 0.000 0.001 -0.003 -0.005 0.001 -0.002 0.000 70 0.004 -0.002 -0.001 -0.001 0.003 0.003 -0.001 0.003 -0.002 0.003 100 -0.005 -0.001 -0.006 0.001 -0.002 -0.003 -0.001 0.000 -0.001 0.001 200 -0.004 -0.002 0.000 0.002 0.000 0.003 -0.002 -0.002 0.000 0.000 400 -0.003 0.000 0.001 -0.001 -0.001 -0.002 -0.001 0.000 0.001 0.000 600 -0.002 -0.001 -0.001 -0.002 0.000 0.001 0.000 0.001 0.001 0.001 800 -0.001 -0.001 0.000 0.000 0.000 0.000 0.001 0.000 0.000 0.001 10 0.028 0.025 0.002 0.002 0.030 0.025 0.029 0.020 0.019 0.015 rbias 30 0.004 0.001 0.003 0.005 0.011 0.005 0.015 0.001 0.006 0.005 50 0.010 0.000 0.005 0.000 0.003 0.005 0.011 0.003 0.003 0.001 70 0.009 0.003 0.003 0.002 0.007 0.006 0.003 0.006 0.004 0.006 100 0.010 0.003 0.011 0.003 0.005 0.006 0.002 0.001 0.001 0.001 200 0.008 0.004 0.001 0.003 0.000 0.006 0.004 0.003 0.001 0.000 400 0.006 0.001 0.002 0.003 0.001 0.004 0.001 0.001 0.001 0.000 600 0.003 0.003 0.003 0.004 0.001 0.001 0.001 0.002 0.003 0.003 800 0.003 0.002 0.000 0.000 0.000 0.000 0.003 0.001 0.000 0.002 10 0.426 0.337 0.300 0.253 0.240 0.229 0.215 0.215 0.206 0.204 RMSE 30 0.262 0.193 0.169 0.149 0.141 0.132 0.123 0.118 0.118 0.117 50 0.200 0.149 0.134 0.113 0.109 0.104 0.097 0.093 0.090 0.089 70 0.165 0.127 0.112 0.099 0.092 0.084 0.080 0.079 0.078 0.078 100 0.141 0.106 0.096 0.082 0.076 0.071 0.068 0.062 0.067 0.062 200 0.097 0.076 0.067 0.058 0.052 0.051 0.048 0.046 0.044 0.044 400 0.072 0.054 0.048 0.041 0.039 0.035 0.036 0.033 0.033 0.033 600 0.056 0.043 0.038 0.033 0.033 0.028 0.027 0.026 0.026 0.026 800 0.048 0.039 0.033 0.029 0.027 0.025 0.024 0.025 0.023 0.023 10 1.818 1.353 1.187 1.007 0.939 0.880 0.836 0.816 0.798 0.789 width 30 1.020 0.771 0.667 0.585 0.548 0.512 0.485 0.474 0.465 0.458 50 0.783 0.595 0.522 0.454 0.423 0.397 0.378 0.367 0.361 0.355 70 0.660 0.503 0.442 0.386 0.358 0.338 0.319 0.310 0.305 0.301 100 0.549 0.421 0.368 0.323 0.300 0.282 0.267 0.260 0.255 0.252 200 0.388 0.299 0.262 0.228 0.212 0.200 0.189 0.184 0.181 0.178 400 0.274 0.211 0.185 0.161 0.150 0.141 0.134 0.130 0.128 0.126 600 0.224 0.172 0.152 0.132 0.123 0.115 0.109 0.106 0.104 0.103 800 0.194 0.149 0.131 0.114 0.106 0.100 0.095 0.092 0.090 0.089 10 0.952 0.938 0.933 0.927 0.926 0.912 0.913 0.919 0.924 0.911 CP 30 0.951 0.957 0.950 0.944 0.949 0.940 0.942 0.944 0.933 0.940 50 0.945 0.936 0.948 0.959 0.952 0.933 0.939 0.940 0.953 0.945 70 0.959 0.949 0.946 0.946 0.947 0.944 0.949 0.939 0.948 0.935 100 0.945 0.953 0.935 0.940 0.950 0.944 0.943 0.963 0.944 0.957 200 0.960 0.957 0.954 0.952 0.958 0.938 0.949 0.959 0.951 0.951 400 0.946 0.952 0.942 0.945 0.949 0.949 0.940 0.962 0.950 0.941 600 0.951 0.952 0.963 0.958 0.946 0.959 0.953 0.953 0.949 0.960 800 0.954 0.940 0.950 0.951 0.948 0.948 0.944 0.933 0.949 0.947 10 0.038 0.008 0.003 0.004 0.000 -0.004 -0.001 -0.006 -0.002 -0.003 SE-SD bias 30 -0.002 0.004 0.001 0.000 -0.001 -0.001 0.000 0.003 0.000 -0.001 50 0.000 0.003 -0.001 0.003 -0.001 -0.003 -0.001 0.001 0.002 0.001 70 0.004 0.002 0.001 -0.001 -0.001 0.002 0.001 0.000 0.000 -0.001 100 -0.001 0.001 -0.002 0.000 0.000 0.001 0.000 0.004 -0.002 0.002 200 0.002 0.000 0.000 0.001 0.002 0.000 0.000 0.001 0.002 0.001 400 -0.002 0.000 -0.001 0.000 0.000 0.001 -0.002 0.000 0.000 -0.001 600 0.001 0.001 0.001 0.000 -0.002 0.001 0.000 0.001 0.000 0.001 800 0.001 -0.001 0.000 0.000 0.000 0.000 0.000 -0.001 0.000 0.000

附表18 研究二平衡设计中且 W i为连续变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

附表18 研究二平衡设计中且 W i为连续变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

注：J 表示水平1 样本量，I 表示水平2 样本量，criteria 表示各评价指标。rbias 中加粗的为其值小于0.1 的结果，width 中加粗的为其值小于0.12 的结果，CP 中加粗的为其值大于0.925 的结果。

criteria I J 10 20 30 50 70 100 150 200 250 300 10 0.031 -0.006 0.001 0.000 -0.003 0.013 0.003 0.000 -0.004 0.001 bias 30 0.001 -0.004 0.000 0.003 0.000 -0.001 0.002 0.001 0.001 0.002 50 0.001 0.004 -0.005 0.004 -0.001 0.000 0.000 -0.003 0.001 0.002 70 -0.001 0.002 0.002 -0.001 0.000 0.001 0.000 0.000 0.000 0.001 100 0.000 0.002 -0.001 0.002 0.001 0.001 0.002 0.001 0.001 0.001 200 0.002 0.002 0.000 0.001 -0.001 -0.002 0.000 0.000 0.000 0.001 400 0.001 0.001 0.000 0.000 0.000 0.000 -0.001 0.000 0.001 0.000 600 0.001 0.000 0.000 0.000 0.000 0.002 0.000 0.000 0.000 0.000 800 0.001 0.000 -0.001 0.000 0.000 0.000 0.000 0.000 0.000 0.000 10 0.061 0.012 0.002 0.001 0.007 0.026 0.005 0.001 0.009 0.003 rbias 30 0.003 0.008 0.000 0.006 0.000 0.002 0.005 0.003 0.002 0.003 50 0.001 0.008 0.011 0.009 0.001 0.000 0.001 0.005 0.003 0.003 70 0.002 0.003 0.004 0.003 0.000 0.003 0.001 0.000 0.001 0.002 100 0.001 0.004 0.002 0.003 0.002 0.001 0.004 0.002 0.003 0.003 200 0.004 0.005 0.000 0.001 0.002 0.003 0.001 0.001 0.000 0.001 400 0.002 0.002 0.000 0.001 0.001 0.000 0.002 0.000 0.002 0.001 600 0.002 0.000 0.000 0.001 0.001 0.003 0.001 0.001 0.001 0.001 800 0.001 0.001 0.001 0.000 0.001 0.000 0.000 0.000 0.000 0.001 10 0.264 0.201 0.174 0.164 0.147 0.135 0.132 0.120 0.123 0.119 RMSE 30 0.139 0.099 0.089 0.080 0.072 0.071 0.065 0.063 0.064 0.062 50 0.104 0.079 0.069 0.059 0.057 0.052 0.050 0.050 0.047 0.047 70 0.089 0.067 0.056 0.050 0.047 0.044 0.041 0.040 0.039 0.039 100 0.071 0.054 0.049 0.043 0.040 0.037 0.034 0.035 0.032 0.032 200 0.049 0.039 0.033 0.028 0.027 0.026 0.023 0.024 0.023 0.023 400 0.036 0.026 0.024 0.020 0.020 0.018 0.018 0.017 0.017 0.016 600 0.028 0.022 0.020 0.017 0.016 0.015 0.014 0.013 0.014 0.013 800 0.025 0.019 0.016 0.014 0.014 0.013 0.013 0.012 0.012 0.012 10 1.053 0.784 0.677 0.592 0.537 0.508 0.485 0.468 0.465 0.453 width 30 0.533 0.400 0.351 0.307 0.284 0.268 0.255 0.251 0.242 0.240 50 0.401 0.306 0.266 0.234 0.217 0.203 0.194 0.189 0.184 0.182 70 0.334 0.255 0.224 0.196 0.184 0.172 0.162 0.158 0.154 0.154 100 0.278 0.213 0.188 0.164 0.151 0.143 0.136 0.132 0.129 0.127 200 0.195 0.150 0.133 0.114 0.107 0.100 0.095 0.093 0.091 0.090 400 0.138 0.106 0.093 0.081 0.075 0.071 0.067 0.065 0.064 0.063 600 0.112 0.086 0.076 0.066 0.062 0.058 0.055 0.053 0.052 0.052 800 0.097 0.075 0.066 0.057 0.053 0.050 0.047 0.046 0.045 0.045 10 0.949 0.940 0.942 0.930 0.927 0.911 0.916 0.929 0.932 0.921 CP 30 0.936 0.949 0.947 0.951 0.939 0.932 0.938 0.939 0.938 0.937 50 0.948 0.941 0.949 0.947 0.938 0.944 0.946 0.942 0.954 0.947 70 0.934 0.936 0.946 0.951 0.945 0.947 0.943 0.947 0.949 0.949 100 0.951 0.943 0.949 0.944 0.944 0.952 0.950 0.944 0.950 0.944 200 0.945 0.950 0.964 0.959 0.950 0.947 0.958 0.952 0.957 0.948 400 0.939 0.955 0.959 0.954 0.942 0.949 0.948 0.953 0.946 0.956 600 0.958 0.946 0.937 0.947 0.948 0.932 0.958 0.947 0.939 0.945 800 0.952 0.956 0.947 0.956 0.953 0.945 0.936 0.951 0.948 0.949 10 0.007 -0.001 -0.001 -0.013 -0.010 -0.005 -0.008 -0.001 -0.004 -0.004 SE-SD bias 30 -0.003 0.003 0.000 -0.001 0.001 -0.003 0.000 0.001 -0.002 0.000 50 -0.002 -0.001 -0.001 0.001 -0.001 0.000 -0.001 -0.001 0.000 -0.001 70 -0.004 -0.002 0.001 0.000 0.000 0.000 0.001 0.000 0.000 0.001 100 0.000 0.001 -0.001 -0.001 -0.001 0.000 0.000 -0.002 0.001 0.000 200 0.000 0.000 0.001 0.001 0.000 0.000 0.001 0.000 0.001 0.000 400 -0.001 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 600 0.001 0.000 -0.001 0.000 0.000 0.000 0.000 0.000 0.000 0.000 800 0.000 0.000 0.000 0.000 0.000 0.000 -0.001 0.000 0.000 0.000

附表19 研究二非平衡设计中且 Wi 为分类变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

附表19 研究二非平衡设计中且 Wi 为分类变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

注：J 表示水平1 样本量，I 表示水平2 样本量，criteria 表示各评价指标。rbias 中加粗的为其值小于0.1 的结果，width 中加粗的为其值小于0.18 的结果，CP 中加粗的为其值大于0.925 的结果。

criteria I J 10 20 30 50 70 100 150 200 250 300 10 -0.003 0.010 -0.008 -0.019 -0.018 -0.037 -0.025 -0.020 -0.017 -0.012 bias 30 -0.016 0.002 -0.012 -0.002 0.006 -0.013 0.000 0.006 -0.003 -0.007 50 -0.001 0.001 -0.005 -0.005 0.007 0.001 0.008 0.003 -0.001 0.000 70 0.002 0.003 -0.008 0.003 0.004 -0.004 0.000 -0.003 0.001 -0.006 100 0.001 -0.007 0.001 0.000 0.002 0.001 -0.001 -0.001 -0.005 0.000 200 -0.002 -0.004 -0.001 -0.002 0.000 -0.002 0.002 -0.001 -0.002 0.000 400 0.003 0.000 0.001 0.002 0.000 0.003 0.001 -0.001 0.001 0.001 600 0.001 0.002 0.000 -0.001 -0.001 0.001 -0.001 0.000 -0.001 0.000 800 -0.001 -0.002 0.000 0.000 -0.001 0.002 -0.001 0.001 0.001 -0.001 10 0.006 0.020 0.016 0.039 0.035 0.074 0.051 0.040 0.035 0.024 rbias 30 0.032 0.003 0.023 0.005 0.012 0.025 0.001 0.012 0.006 0.014 50 0.002 0.003 0.010 0.009 0.014 0.001 0.015 0.005 0.001 0.000 70 0.004 0.005 0.017 0.006 0.007 0.009 0.001 0.005 0.002 0.012 100 0.002 0.014 0.001 0.000 0.003 0.002 0.003 0.002 0.009 0.001 200 0.005 0.007 0.002 0.004 0.000 0.004 0.003 0.001 0.004 0.000 400 0.006 0.000 0.002 0.004 0.001 0.005 0.002 0.003 0.001 0.002 600 0.002 0.004 0.000 0.001 0.002 0.003 0.002 0.000 0.002 0.001 800 0.002 0.004 0.001 0.001 0.002 0.003 0.002 0.002 0.001 0.002 10 0.557 0.430 0.369 0.312 0.295 0.278 0.272 0.262 0.258 0.264 RMSE 30 0.329 0.244 0.217 0.185 0.178 0.164 0.153 0.148 0.149 0.148 50 0.252 0.194 0.168 0.148 0.136 0.127 0.123 0.116 0.114 0.117 70 0.211 0.164 0.147 0.123 0.112 0.107 0.106 0.099 0.099 0.093 100 0.174 0.135 0.114 0.103 0.098 0.087 0.087 0.083 0.082 0.078 200 0.122 0.093 0.083 0.076 0.068 0.065 0.062 0.060 0.056 0.055 400 0.086 0.066 0.058 0.050 0.049 0.044 0.042 0.041 0.040 0.039 600 0.071 0.055 0.050 0.040 0.040 0.037 0.034 0.034 0.034 0.032 800 0.061 0.048 0.041 0.038 0.033 0.033 0.030 0.028 0.029 0.029 10 2.267 1.680 1.477 1.251 1.177 1.098 1.047 1.017 0.999 0.981 width 30 1.259 0.960 0.836 0.738 0.682 0.643 0.610 0.592 0.582 0.574 50 0.977 0.744 0.654 0.568 0.529 0.497 0.472 0.460 0.450 0.443 70 0.824 0.627 0.555 0.483 0.447 0.421 0.400 0.388 0.380 0.376 100 0.686 0.528 0.464 0.404 0.376 0.352 0.334 0.324 0.319 0.315 200 0.485 0.372 0.328 0.286 0.265 0.249 0.237 0.230 0.226 0.223 400 0.343 0.263 0.231 0.202 0.188 0.177 0.167 0.162 0.159 0.158 600 0.280 0.216 0.189 0.165 0.153 0.144 0.137 0.133 0.130 0.129 800 0.243 0.186 0.164 0.143 0.133 0.125 0.118 0.115 0.113 0.111 10 0.948 0.933 0.931 0.933 0.927 0.919 0.915 0.918 0.913 0.902 CP 30 0.941 0.945 0.937 0.950 0.939 0.936 0.940 0.948 0.938 0.928 50 0.939 0.944 0.949 0.941 0.942 0.946 0.945 0.940 0.943 0.936 70 0.943 0.942 0.940 0.949 0.955 0.943 0.936 0.951 0.942 0.951 100 0.960 0.948 0.953 0.946 0.945 0.959 0.947 0.950 0.951 0.957 200 0.955 0.957 0.957 0.944 0.948 0.945 0.947 0.937 0.951 0.954 400 0.954 0.948 0.953 0.951 0.951 0.948 0.955 0.966 0.952 0.959 600 0.950 0.952 0.943 0.955 0.947 0.941 0.957 0.942 0.948 0.956 800 0.948 0.941 0.958 0.948 0.954 0.942 0.953 0.956 0.951 0.952 10 0.021 -0.002 0.008 0.008 0.005 0.004 -0.004 -0.002 -0.003 -0.013 SE-SD bias 30 -0.008 0.001 -0.004 0.003 -0.004 0.000 0.003 0.003 -0.001 -0.001 50 -0.003 -0.004 -0.001 -0.003 -0.001 -0.001 -0.003 0.001 0.000 -0.004 70 -0.001 -0.004 -0.006 0.000 0.003 0.000 -0.004 0.000 -0.002 0.003 100 0.001 0.000 0.005 0.000 -0.002 0.003 -0.002 0.000 -0.001 0.003 200 0.002 0.002 0.001 -0.003 -0.001 -0.002 -0.002 -0.002 0.002 0.002 400 0.002 0.001 0.001 0.001 -0.001 0.001 0.000 0.000 0.000 0.001 600 0.000 0.000 -0.002 0.002 -0.001 0.000 0.001 0.000 -0.001 0.001 800 0.001 -0.001 0.001 -0.001 0.000 -0.001 0.000 0.001 0.000 0.000

附表20 研究二平衡设计大且 W i为分类变量时线性混合效应模型水平2 自变量调节效应量及其标准误估计准确性

注：J 表示水平1 样本量，I 表示水平2 样本量，criteria 表示各评价指标。rbias 中加粗的为其值小于0.1 的结果，width 中加粗的为其值小于0.3 的结果，CP 中加粗的为其值大于0.925 的结果。

criteria I J 10 20 30 50 70 100 150 200 250 300 10 -0.009 -0.044 -0.033 -0.009 -0.007 -0.028 -0.015 -0.016 -0.034 -0.014 bias 30 -0.015 -0.011 -0.013 0.003 -0.015 -0.010 -0.010 -0.004 -0.013 0.003 50 0.005 -0.001 -0.002 0.005 0.001 0.006 0.003 -0.002 -0.005 0.005 70 -0.002 -0.003 -0.002 -0.002 0.001 0.001 -0.008 -0.007 -0.005 0.001 100 0.001 -0.004 -0.002 -0.005 0.003 -0.008 0.001 -0.002 -0.009 0.001 200 0.003 0.000 -0.008 0.000 0.000 0.002 -0.001 0.003 0.000 -0.001 400 0.001 0.001 0.001 -0.002 0.001 -0.002 -0.005 -0.001 -0.002 0.000 600 -0.001 0.000 0.000 0.001 -0.001 -0.001 0.000 -0.001 0.000 0.000 800 0.001 0.000 0.003 0.001 0.000 -0.001 0.004 -0.001 -0.001 0.000 10 0.018 0.088 0.066 0.019 0.013 0.057 0.031 0.033 0.068 0.029 rbias 30 0.029 0.021 0.026 0.007 0.030 0.020 0.021 0.007 0.025 0.006 50 0.010 0.003 0.003 0.010 0.001 0.012 0.006 0.005 0.011 0.010 70 0.004 0.006 0.003 0.004 0.001 0.002 0.016 0.014 0.010 0.002 100 0.002 0.007 0.004 0.010 0.006 0.015 0.002 0.004 0.018 0.002 200 0.005 0.000 0.016 0.000 0.000 0.004 0.001 0.007 0.000 0.002 400 0.001 0.001 0.001 0.005 0.001 0.003 0.010 0.002 0.003 0.000 600 0.003 0.000 0.001 0.002 0.002 0.003 0.000 0.002 0.000 0.001 800 0.003 0.000 0.005 0.001 0.000 0.003 0.007 0.002 0.003 0.000 10 0.493 0.432 0.393 0.366 0.356 0.334 0.334 0.329 0.323 0.332 RMSE 30 0.291 0.239 0.225 0.209 0.203 0.201 0.191 0.179 0.186 0.181 50 0.226 0.190 0.171 0.165 0.156 0.150 0.152 0.146 0.149 0.142 70 0.199 0.159 0.149 0.135 0.131 0.131 0.127 0.124 0.126 0.122 100 0.163 0.134 0.121 0.109 0.108 0.109 0.102 0.103 0.104 0.104 200 0.113 0.094 0.090 0.082 0.077 0.073 0.074 0.074 0.075 0.071 400 0.080 0.066 0.062 0.057 0.059 0.055 0.052 0.053 0.051 0.049 600 0.063 0.056 0.053 0.046 0.044 0.042 0.043 0.043 0.043 0.041 800 0.058 0.047 0.044 0.039 0.039 0.038 0.037 0.036 0.036 0.036 10 2.025 1.661 1.494 1.400 1.354 1.323 1.286 1.279 1.270 1.260 width 30 1.152 0.951 0.884 0.819 0.787 0.767 0.750 0.744 0.738 0.736 50 0.890 0.747 0.683 0.634 0.615 0.596 0.583 0.576 0.571 0.569 70 0.754 0.629 0.579 0.538 0.519 0.504 0.492 0.486 0.483 0.481 100 0.635 0.526 0.484 0.449 0.434 0.422 0.413 0.407 0.404 0.402 200 0.446 0.371 0.343 0.318 0.307 0.298 0.292 0.288 0.286 0.284 400 0.316 0.263 0.243 0.225 0.217 0.211 0.206 0.204 0.202 0.201 600 0.258 0.215 0.198 0.184 0.177 0.172 0.168 0.166 0.165 0.164 800 0.224 0.186 0.172 0.159 0.154 0.149 0.146 0.144 0.143 0.142 10 0.940 0.920 0.927 0.913 0.912 0.917 0.911 0.925 0.908 0.908 CP SE-SD bias 30 0.931 0.948 0.946 0.940 0.939 0.933 0.941 0.959 0.940 0.949 50 0.935 0.952 0.948 0.940 0.952 0.946 0.940 0.935 0.937 0.955 70 0.940 0.949 0.945 0.952 0.948 0.940 0.945 0.953 0.945 0.948 100 0.949 0.950 0.955 0.948 0.958 0.942 0.961 0.959 0.943 0.940 200 0.947 0.952 0.937 0.946 0.953 0.958 0.949 0.960 0.933 0.952 400 0.955 0.950 0.944 0.944 0.945 0.941 0.946 0.942 0.954 0.954 600 0.961 0.939 0.933 0.958 0.955 0.951 0.953 0.944 0.943 0.943 800 0.944 0.957 0.953 0.960 0.956 0.953 0.954 0.961 0.959 0.952 10 0.023 -0.006 -0.011 -0.009 -0.011 0.004 -0.006 -0.002 0.002 -0.010 30 0.003 0.004 0.001 0.000 -0.002 -0.006 0.001 0.010 0.003 0.006 50 0.001 0.000 0.003 -0.003 0.001 0.002 -0.004 0.001 -0.003 0.003 70 -0.007 0.002 -0.002 0.002 0.001 -0.002 -0.001 0.001 -0.003 0.001 100 -0.001 0.000 0.003 0.006 0.003 -0.001 0.003 0.001 -0.001 -0.002 200 0.001 0.000 -0.003 -0.001 0.002 0.003 0.001 -0.001 -0.002 0.001 400 0.000 0.001 0.000 0.000 -0.003 -0.002 0.001 -0.001 0.000 0.002 600 0.003 -0.001 -0.002 0.001 0.001 0.001 0.000 -0.001 -0.001 0.000 800 -0.001 0.000 0.000 0.002 0.001 0.000 0.000 0.001 0.000 0.000

与研究1 不同, 研究1 中水平1 自变量(实验效应)估计准确性更受水平1 样本量影响, 而研究2 中跨水平交互效应估计准确性更受水平2 样本量影响。在Wi为分类变量且为中等()的情况下, 根据公式(15), 计算效应量小和大条件的标准值分别为0.06 (0.2 ×0.3)和0.24 (0.8 ×0.3)。则定义可接受的最宽95% CI 宽度为0.24 - 0.06 =0.18。从附表17 看出, 部分条件下95% CI 过宽。只有当水平2 样本量为400, 且水平1 样本量在50及以上, 或者水平2 样本量在600 及以上, 且水平1样本量在20 及以上时, 能够满足95% CI 宽度小于0.18。

Wi为分类变量和连续变量得到的bias, rbias,95%CP 和SE-SD bias 的结果非常一致, 都较小。Wi为连续变量时得到的RMSE 较小(见附表18), 95%CI 较窄。根据公式(15), 效应量为小和大时γ11分别为0.03 (0.1 ×0.3)和0.15 (0.5 ×0.1)。定义可接受的最宽95% CI 宽度为0.15 - 0.03 = 0.12。

此外, 与平衡设计下的结果相比, 非平衡设计下的RMSE 更大, 95% CI 更宽。

5.3.4 随机效应估计准确性结果

附表21～25 (在线补充材料1)呈现了随机效应估计rbias 结果。从表中看出, 首先, 与研究1 类似,大小、Wi类型和是否为平衡设计基本不会影响σ2和估计的准确性。σ2估计值的rbias 在各样本量条件下均达到小于0.1 的标准。其次, 当Wi为分类变量时, 随着增加,的估计准确性降低,的估计准确性增加。具体来看, 当小时, 几乎所有样本量条件下估计值的rbias 都大于0.1。进一步计算其bias 发现, 此时大部分情况下会存在高估的问题。当大时, 所有样本量条件下估计值的rbias 都大于0.1。进一步计算其bias 发现, 此时大部分情况下存在高估的问题。最后, 当Wi为连续变量时,的估计准确性略高于分类变量的情况。

附表21 研究二平衡设计小且 Wi 为分类变量时线性混合效应模型随机效应估计rbias

注：J 表示水平1 样本量，I 表示水平2 样本量，parameter 表示各随机效应。表中加粗的为其值小于0.1 的结果。

Parameter I J 10 20 30 50 70 100 150 200 250 300 10 0.065 0.035 0.027 0.020 0.016 0.014 0.010 0.009 0.008 0.007 2σ 30 0.031 0.015 0.012 0.007 0.006 0.005 0.004 0.003 0.003 0.002 50 0.022 0.012 0.008 0.006 0.004 0.003 0.002 0.002 0.002 0.002 70 0.019 0.010 0.006 0.004 0.003 0.002 0.002 0.001 0.001 0.001 100 0.016 0.008 0.006 0.004 0.003 0.002 0.001 0.001 0.001 0.001 200 0.011 0.005 0.004 0.002 0.002 0.001 0.001 0.001 0.001 0.001 400 0.008 0.004 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 600 0.007 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 800 0.006 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 10 0.421 0.319 0.266 0.215 0.191 0.170 0.153 0.148 0.134 0.138 2 τ 00 2 11τ 30 0.232 0.157 0.124 0.101 0.088 0.074 0.066 0.063 0.054 0.052 50 0.164 0.121 0.100 0.072 0.065 0.053 0.045 0.041 0.039 0.037 70 0.145 0.102 0.079 0.062 0.056 0.045 0.037 0.033 0.032 0.030 100 0.120 0.082 0.067 0.053 0.046 0.037 0.031 0.028 0.026 0.023 200 0.083 0.059 0.045 0.036 0.031 0.025 0.021 0.018 0.018 0.015 400 0.060 0.041 0.034 0.026 0.022 0.019 0.015 0.013 0.013 0.012 600 0.050 0.033 0.027 0.021 0.018 0.015 0.013 0.011 0.010 0.010 800 0.045 0.029 0.022 0.018 0.017 0.013 0.011 0.010 0.009 0.009 10 11.006 5.236 3.678 2.229 1.795 1.308 1.106 0.886 0.838 0.752 30 5.432 2.613 2.046 1.392 1.054 0.851 0.667 0.603 0.525 0.450 50 4.032 1.983 1.514 1.142 0.905 0.723 0.556 0.452 0.371 0.333 70 3.324 1.805 1.369 0.984 0.796 0.641 0.482 0.377 0.325 0.287 100 2.906 1.632 1.247 0.854 0.711 0.534 0.399 0.320 0.274 0.243 200 2.142 1.316 0.933 0.644 0.544 0.395 0.284 0.220 0.194 0.169 400 1.707 0.999 0.727 0.510 0.368 0.286 0.209 0.162 0.138 0.122 600 1.503 0.825 0.590 0.419 0.300 0.230 0.172 0.136 0.108 0.102 800 1.325 0.751 0.571 0.354 0.272 0.198 0.137 0.111 0.102 0.086 10 0.559 0.328 0.259 0.194 0.156 0.130 0.109 0.088 0.081 0.073 2 00ω 30 0.283 0.166 0.139 0.106 0.086 0.070 0.058 0.050 0.044 0.040 50 0.238 0.138 0.113 0.083 0.065 0.054 0.044 0.038 0.033 0.029 70 0.209 0.121 0.089 0.068 0.054 0.046 0.036 0.033 0.029 0.026 100 0.184 0.107 0.079 0.056 0.048 0.039 0.029 0.027 0.023 0.021 200 0.158 0.082 0.062 0.043 0.034 0.028 0.023 0.018 0.017 0.015 400 0.134 0.065 0.048 0.033 0.027 0.021 0.016 0.014 0.012 0.011 600 0.126 0.063 0.041 0.032 0.022 0.018 0.014 0.012 0.010 0.010 800 0.128 0.063 0.042 0.027 0.021 0.016 0.013 0.010 0.009 0.008

附表22 研究二平衡设计中且 Wi 为分类变量时线性混合效应模型随机效应估计rbias

附表22 研究二平衡设计中且 Wi 为分类变量时线性混合效应模型随机效应估计rbias

注：J 表示水平1 样本量，I 表示水平2 样本量，parameter 表示各随机效应。表中加粗的为其值小于0.1 的结果。

Parameter I J 10 20 30 50 70 100 150 200 250 300 10 0.065 0.038 0.028 0.020 0.015 0.013 0.010 0.009 0.008 0.007 2σ 2 τ 00 2 τ 11 2 00ω 30 0.032 0.018 0.012 0.008 0.006 0.005 0.004 0.003 0.003 0.002 50 0.025 0.013 0.009 0.006 0.004 0.003 0.002 0.002 0.002 0.001 70 0.021 0.010 0.007 0.004 0.003 0.003 0.002 0.001 0.001 0.001 100 0.017 0.009 0.006 0.004 0.003 0.002 0.001 0.001 0.001 0.001 200 0.013 0.006 0.004 0.002 0.002 0.001 0.001 0.001 0.001 0.000 400 0.008 0.004 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 600 0.008 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 800 0.006 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 10 0.434 0.323 0.267 0.222 0.199 0.181 0.163 0.153 0.158 0.149 30 0.249 0.161 0.136 0.112 0.097 0.090 0.080 0.076 0.076 0.072 50 0.183 0.126 0.109 0.087 0.077 0.073 0.065 0.066 0.060 0.063 70 0.157 0.111 0.092 0.074 0.066 0.065 0.058 0.057 0.057 0.057 100 0.135 0.095 0.080 0.070 0.062 0.060 0.057 0.056 0.054 0.054 200 0.099 0.071 0.065 0.058 0.054 0.053 0.054 0.053 0.052 0.053 400 0.078 0.062 0.058 0.054 0.053 0.052 0.051 0.053 0.053 0.052 600 0.068 0.056 0.054 0.053 0.053 0.054 0.051 0.053 0.053 0.052 800 0.063 0.057 0.054 0.053 0.053 0.053 0.053 0.053 0.053 0.053 10 1.434 0.942 0.776 0.594 0.502 0.430 0.358 0.302 0.265 0.262 30 0.940 0.639 0.467 0.335 0.288 0.229 0.176 0.156 0.139 0.126 50 0.816 0.510 0.362 0.252 0.214 0.172 0.131 0.122 0.106 0.092 70 0.685 0.435 0.301 0.226 0.179 0.140 0.114 0.097 0.084 0.079 100 0.589 0.345 0.268 0.179 0.150 0.122 0.100 0.082 0.072 0.066 200 0.443 0.258 0.185 0.126 0.105 0.088 0.066 0.059 0.051 0.045 400 0.328 0.176 0.130 0.096 0.071 0.059 0.047 0.039 0.034 0.032 600 0.270 0.143 0.105 0.074 0.062 0.047 0.038 0.033 0.029 0.026 800 0.226 0.123 0.088 0.060 0.052 0.043 0.033 0.029 0.025 0.024 10 0.498 0.310 0.249 0.196 0.159 0.133 0.110 0.090 0.082 0.070 30 0.306 0.184 0.146 0.102 0.085 0.071 0.058 0.050 0.043 0.039 50 0.238 0.139 0.109 0.080 0.065 0.054 0.043 0.037 0.034 0.030 70 0.210 0.118 0.093 0.068 0.056 0.046 0.037 0.032 0.028 0.026 100 0.189 0.101 0.078 0.055 0.049 0.039 0.030 0.027 0.022 0.021 200 0.157 0.083 0.062 0.043 0.035 0.028 0.023 0.019 0.017 0.016 400 0.128 0.066 0.049 0.034 0.026 0.022 0.016 0.013 0.012 0.011 600 0.128 0.063 0.045 0.029 0.024 0.018 0.014 0.011 0.010 0.009 800 0.119 0.061 0.041 0.028 0.022 0.016 0.013 0.010 0.009 0.008

附表23 研究二平衡设计中等且 Wi 为连续变量时线性混合效应模型随机效应估计rbias

附表23 研究二平衡设计中等且 Wi 为连续变量时线性混合效应模型随机效应估计rbias

注：J 表示水平1 样本量，I 表示水平2 样本量，parameter 表示各随机效应。表中加粗的为其值小于0.1 的结果。

Parameter I J 10 20 30 50 70 100 150 200 250 300 10 0.066 0.038 0.028 0.020 0.016 0.013 0.010 0.009 0.008 0.007 2σ 30 0.031 0.018 0.012 0.008 0.006 0.005 0.004 0.003 0.003 0.002 50 0.024 0.012 0.009 0.006 0.004 0.003 0.002 0.002 0.002 0.001 70 0.021 0.011 0.007 0.005 0.003 0.002 0.002 0.001 0.001 0.001 100 0.018 0.009 0.006 0.004 0.003 0.002 0.001 0.001 0.001 0.001 200 0.013 0.006 0.004 0.002 0.002 0.001 0.001 0.001 0.001 0.000 400 0.009 0.004 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 600 0.007 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 800 0.006 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 10 0.309 0.234 0.199 0.172 0.154 0.146 0.135 0.128 0.119 0.121 2 τ 00 30 0.162 0.110 0.094 0.075 0.068 0.057 0.050 0.047 0.045 0.045 50 0.123 0.085 0.066 0.054 0.048 0.042 0.035 0.032 0.029 0.030 70 0.100 0.068 0.057 0.046 0.039 0.033 0.028 0.026 0.024 0.022 100 0.081 0.059 0.045 0.037 0.031 0.026 0.023 0.020 0.019 0.018 200 0.058 0.040 0.033 0.025 0.023 0.018 0.016 0.014 0.012 0.011 400 0.042 0.028 0.022 0.018 0.015 0.012 0.010 0.009 0.008 0.008 600 0.033 0.024 0.018 0.015 0.011 0.010 0.008 0.007 0.007 0.006 800 0.030 0.020 0.017 0.013 0.011 0.009 0.007 0.006 0.006 0.005 10 1.439 0.982 0.779 0.611 0.520 0.443 0.350 0.301 0.268 0.252 2 11τ 30 0.919 0.602 0.497 0.344 0.283 0.221 0.185 0.155 0.135 0.122 50 0.761 0.494 0.386 0.262 0.206 0.172 0.139 0.122 0.100 0.095 70 0.674 0.408 0.302 0.217 0.171 0.149 0.110 0.097 0.088 0.080 100 0.610 0.350 0.260 0.185 0.147 0.116 0.095 0.077 0.073 0.063 200 0.440 0.256 0.178 0.128 0.103 0.086 0.067 0.057 0.051 0.045 400 0.316 0.173 0.131 0.092 0.075 0.057 0.045 0.041 0.035 0.033 600 0.252 0.141 0.107 0.075 0.059 0.046 0.038 0.032 0.029 0.027 800 0.231 0.122 0.093 0.064 0.052 0.041 0.035 0.028 0.025 0.022 10 0.507 0.324 0.243 0.187 0.153 0.128 0.104 0.096 0.083 0.076 2 00ω 30 0.293 0.187 0.136 0.104 0.087 0.069 0.056 0.049 0.044 0.039 50 0.234 0.142 0.110 0.078 0.062 0.056 0.045 0.037 0.033 0.029 70 0.200 0.126 0.092 0.068 0.055 0.046 0.037 0.031 0.027 0.026 100 0.179 0.103 0.081 0.058 0.047 0.039 0.030 0.025 0.024 0.021 200 0.156 0.082 0.062 0.043 0.034 0.027 0.022 0.019 0.017 0.015 400 0.135 0.067 0.047 0.034 0.027 0.020 0.016 0.014 0.011 0.012 600 0.131 0.066 0.045 0.030 0.023 0.018 0.014 0.012 0.010 0.009 800 0.123 0.061 0.042 0.028 0.020 0.016 0.013 0.010 0.009 0.008

附表24 研究二非平衡设计 中且 Wi 为分类变量时线性混合效应模型随机效应估计rbias

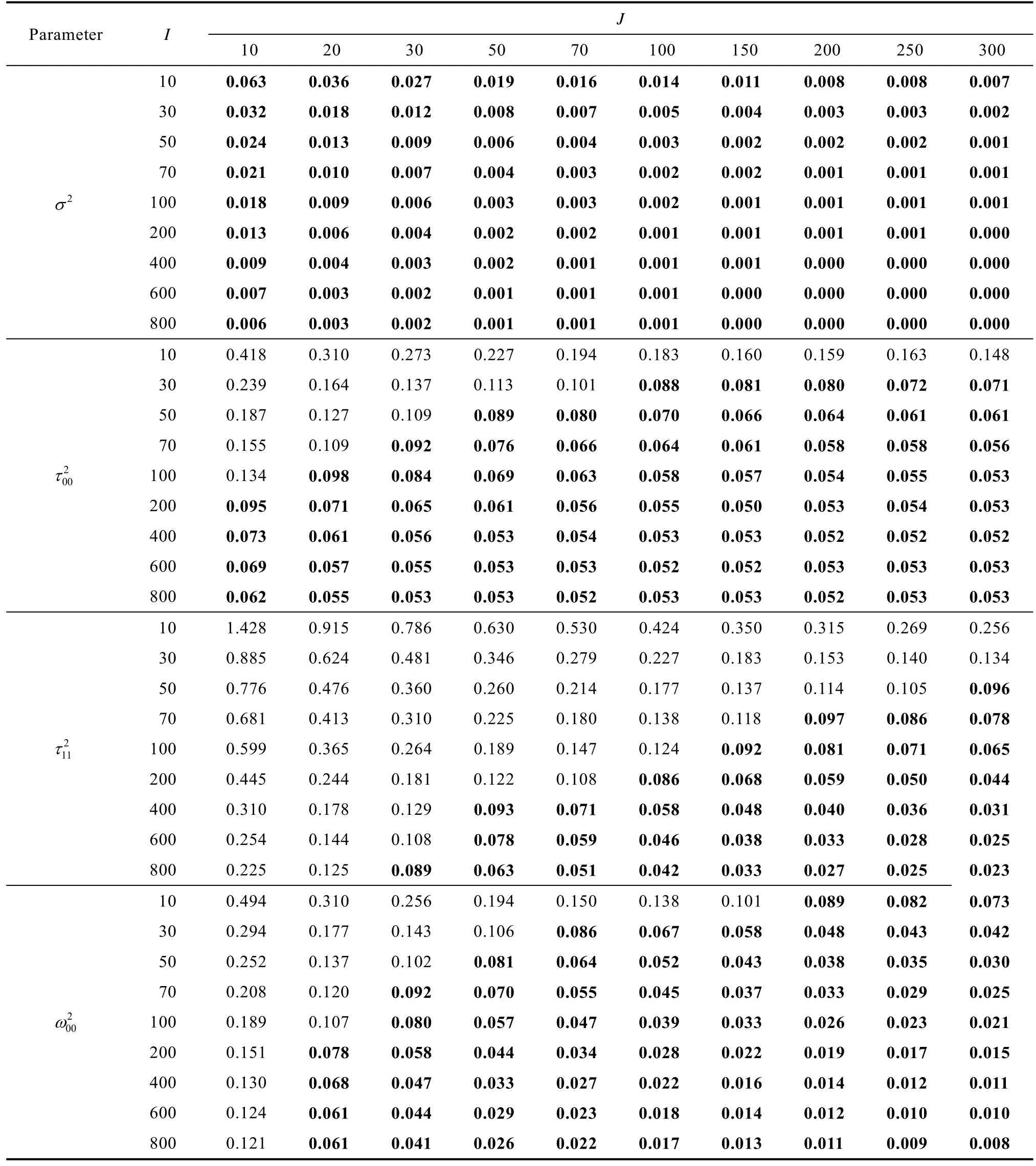
附表24 研究二非平衡设计 中且 Wi 为分类变量时线性混合效应模型随机效应估计rbias

注：J 表示水平1 样本量，I 表示水平2 样本量，parameter 表示各随机效应。表中加粗的为其值小于0.1 的结果。

Parameter I J 10 20 30 50 70 100 150 200 250 300 10 0.063 0.036 0.027 0.019 0.016 0.014 0.011 0.008 0.008 0.007 2σ 30 0.032 0.018 0.012 0.008 0.007 0.005 0.004 0.003 0.003 0.002 50 0.024 0.013 0.009 0.006 0.004 0.003 0.002 0.002 0.002 0.001 70 0.021 0.010 0.007 0.004 0.003 0.002 0.002 0.001 0.001 0.001 100 0.018 0.009 0.006 0.003 0.003 0.002 0.001 0.001 0.001 0.001 200 0.013 0.006 0.004 0.002 0.002 0.001 0.001 0.001 0.001 0.000 400 0.009 0.004 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 600 0.007 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 800 0.006 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 10 0.418 0.310 0.273 0.227 0.194 0.183 0.160 0.159 0.163 0.148 2 τ 00 30 0.239 0.164 0.137 0.113 0.101 0.088 0.081 0.080 0.072 0.071 50 0.187 0.127 0.109 0.089 0.080 0.070 0.066 0.064 0.061 0.061 70 0.155 0.109 0.092 0.076 0.066 0.064 0.061 0.058 0.058 0.056 100 0.134 0.098 0.084 0.069 0.063 0.058 0.057 0.054 0.055 0.053 200 0.095 0.071 0.065 0.061 0.056 0.055 0.050 0.053 0.054 0.053 400 0.073 0.061 0.056 0.053 0.054 0.053 0.053 0.052 0.052 0.052 600 0.069 0.057 0.055 0.053 0.053 0.052 0.052 0.053 0.053 0.053 800 0.062 0.055 0.053 0.053 0.052 0.053 0.053 0.052 0.053 0.053 10 1.428 0.915 0.786 0.630 0.530 0.424 0.350 0.315 0.269 0.256 2 11τ 30 0.885 0.624 0.481 0.346 0.279 0.227 0.183 0.153 0.140 0.134 50 0.776 0.476 0.360 0.260 0.214 0.177 0.137 0.114 0.105 0.096 70 0.681 0.413 0.310 0.225 0.180 0.138 0.118 0.097 0.086 0.078 100 0.599 0.365 0.264 0.189 0.147 0.124 0.092 0.081 0.071 0.065 200 0.445 0.244 0.181 0.122 0.108 0.086 0.068 0.059 0.050 0.044 400 0.310 0.178 0.129 0.093 0.071 0.058 0.048 0.040 0.036 0.031 600 0.254 0.144 0.108 0.078 0.059 0.046 0.038 0.033 0.028 0.025 800 0.225 0.125 0.089 0.063 0.051 0.042 0.033 0.027 0.025 0.023 10 0.494 0.310 0.256 0.194 0.150 0.138 0.101 0.089 0.082 0.073 2 00ω 30 0.294 0.177 0.143 0.106 0.086 0.067 0.058 0.048 0.043 0.042 50 0.252 0.137 0.102 0.081 0.064 0.052 0.043 0.038 0.035 0.030 70 0.208 0.120 0.092 0.070 0.055 0.045 0.037 0.033 0.029 0.025 100 0.189 0.107 0.080 0.057 0.047 0.039 0.033 0.026 0.023 0.021 200 0.151 0.078 0.058 0.044 0.034 0.028 0.022 0.019 0.017 0.015 400 0.130 0.068 0.047 0.033 0.027 0.022 0.016 0.014 0.012 0.011 600 0.124 0.061 0.044 0.029 0.023 0.018 0.014 0.012 0.010 0.010 800 0.121 0.061 0.041 0.026 0.022 0.017 0.013 0.011 0.009 0.008

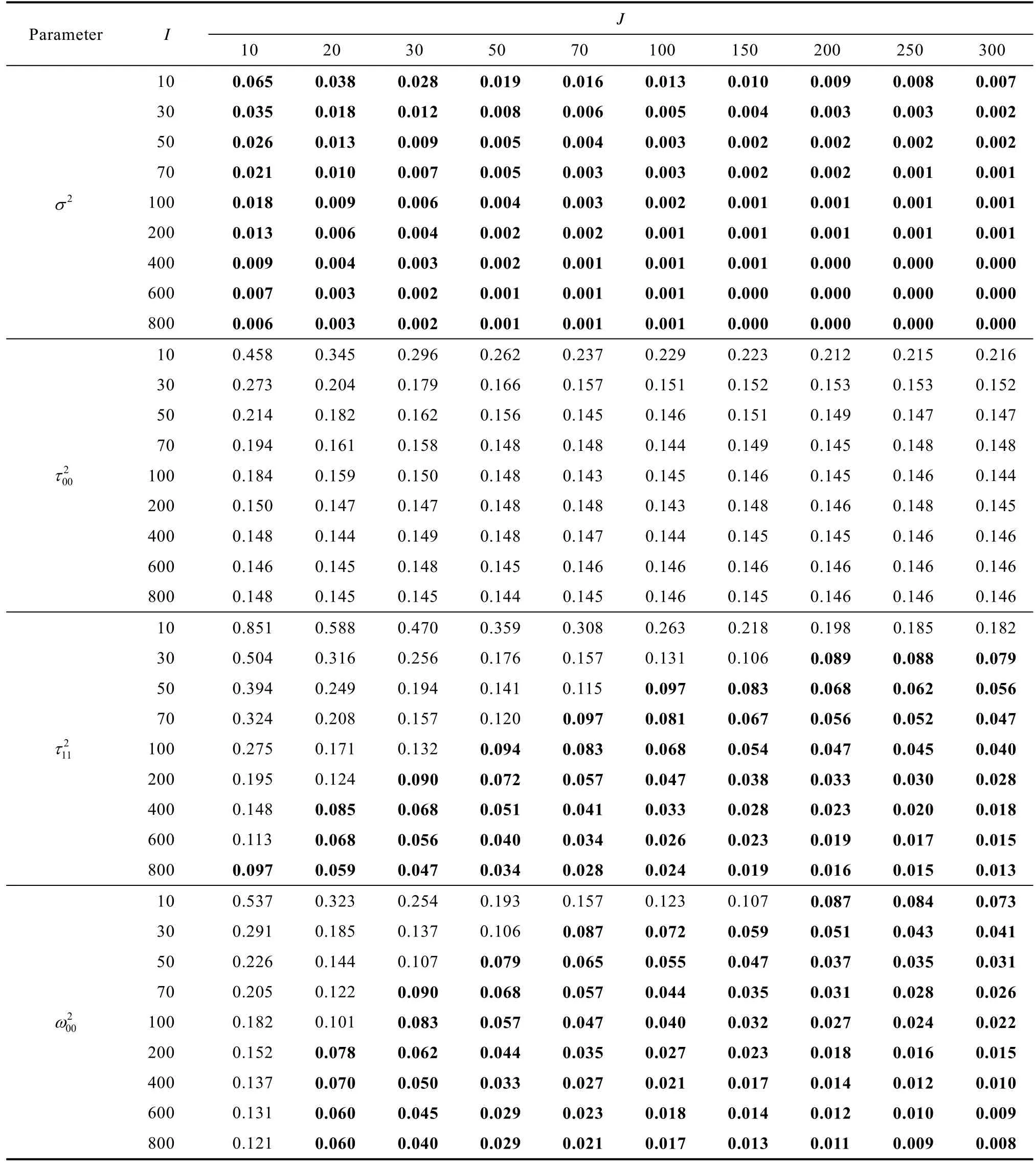
附表25 研究二平衡设计大且 Wi 为分类变量时线性混合效应模型随机效应估计rbias

附表25 研究二平衡设计大且 Wi 为分类变量时线性混合效应模型随机效应估计rbias

注：J 表示水平1 样本量，I 表示水平2 样本量，parameter 表示各随机效应。表中加粗的为其值小于0.1 的结果。

Parameter I J 10 20 30 50 70 100 150 200 250 300 10 0.065 0.038 0.028 0.019 0.016 0.013 0.010 0.009 0.008 0.007 2σ 30 0.035 0.018 0.012 0.008 0.006 0.005 0.004 0.003 0.003 0.002 50 0.026 0.013 0.009 0.005 0.004 0.003 0.002 0.002 0.002 0.002 70 0.021 0.010 0.007 0.005 0.003 0.003 0.002 0.002 0.001 0.001 100 0.018 0.009 0.006 0.004 0.003 0.002 0.001 0.001 0.001 0.001 200 0.013 0.006 0.004 0.002 0.002 0.001 0.001 0.001 0.001 0.001 400 0.009 0.004 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 600 0.007 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 800 0.006 0.003 0.002 0.001 0.001 0.001 0.000 0.000 0.000 0.000 10 0.458 0.345 0.296 0.262 0.237 0.229 0.223 0.212 0.215 0.216 2 τ 00 30 0.273 0.204 0.179 0.166 0.157 0.151 0.152 0.153 0.153 0.152 50 0.214 0.182 0.162 0.156 0.145 0.146 0.151 0.149 0.147 0.147 70 0.194 0.161 0.158 0.148 0.148 0.144 0.149 0.145 0.148 0.148 100 0.184 0.159 0.150 0.148 0.143 0.145 0.146 0.145 0.146 0.144 200 0.150 0.147 0.147 0.148 0.148 0.143 0.148 0.146 0.148 0.145 400 0.148 0.144 0.149 0.148 0.147 0.144 0.145 0.145 0.146 0.146 600 0.146 0.145 0.148 0.145 0.146 0.146 0.146 0.146 0.146 0.146 800 0.148 0.145 0.145 0.144 0.145 0.146 0.145 0.146 0.146 0.146 10 0.851 0.588 0.470 0.359 0.308 0.263 0.218 0.198 0.185 0.182 2 11τ 30 0.504 0.316 0.256 0.176 0.157 0.131 0.106 0.089 0.088 0.079 50 0.394 0.249 0.194 0.141 0.115 0.097 0.083 0.068 0.062 0.056 70 0.324 0.208 0.157 0.120 0.097 0.081 0.067 0.056 0.052 0.047 100 0.275 0.171 0.132 0.094 0.083 0.068 0.054 0.047 0.045 0.040 200 0.195 0.124 0.090 0.072 0.057 0.047 0.038 0.033 0.030 0.028 400 0.148 0.085 0.068 0.051 0.041 0.033 0.028 0.023 0.020 0.018 600 0.113 0.068 0.056 0.040 0.034 0.026 0.023 0.019 0.017 0.015 800 0.097 0.059 0.047 0.034 0.028 0.024 0.019 0.016 0.015 0.013 10 0.537 0.323 0.254 0.193 0.157 0.123 0.107 0.087 0.084 0.073 2 00ω 30 0.291 0.185 0.137 0.106 0.087 0.072 0.059 0.051 0.043 0.041 50 0.226 0.144 0.107 0.079 0.065 0.055 0.047 0.037 0.035 0.031 70 0.205 0.122 0.090 0.068 0.057 0.044 0.035 0.031 0.028 0.026 100 0.182 0.101 0.083 0.057 0.047 0.040 0.032 0.027 0.024 0.022 200 0.152 0.078 0.062 0.044 0.035 0.027 0.023 0.018 0.016 0.015 400 0.137 0.070 0.050 0.033 0.027 0.021 0.017 0.014 0.012 0.010 600 0.131 0.060 0.045 0.029 0.023 0.018 0.014 0.012 0.010 0.009 800 0.121 0.060 0.040 0.029 0.021 0.017 0.013 0.011 0.009 0.008

5.3.5 样本量规划建议

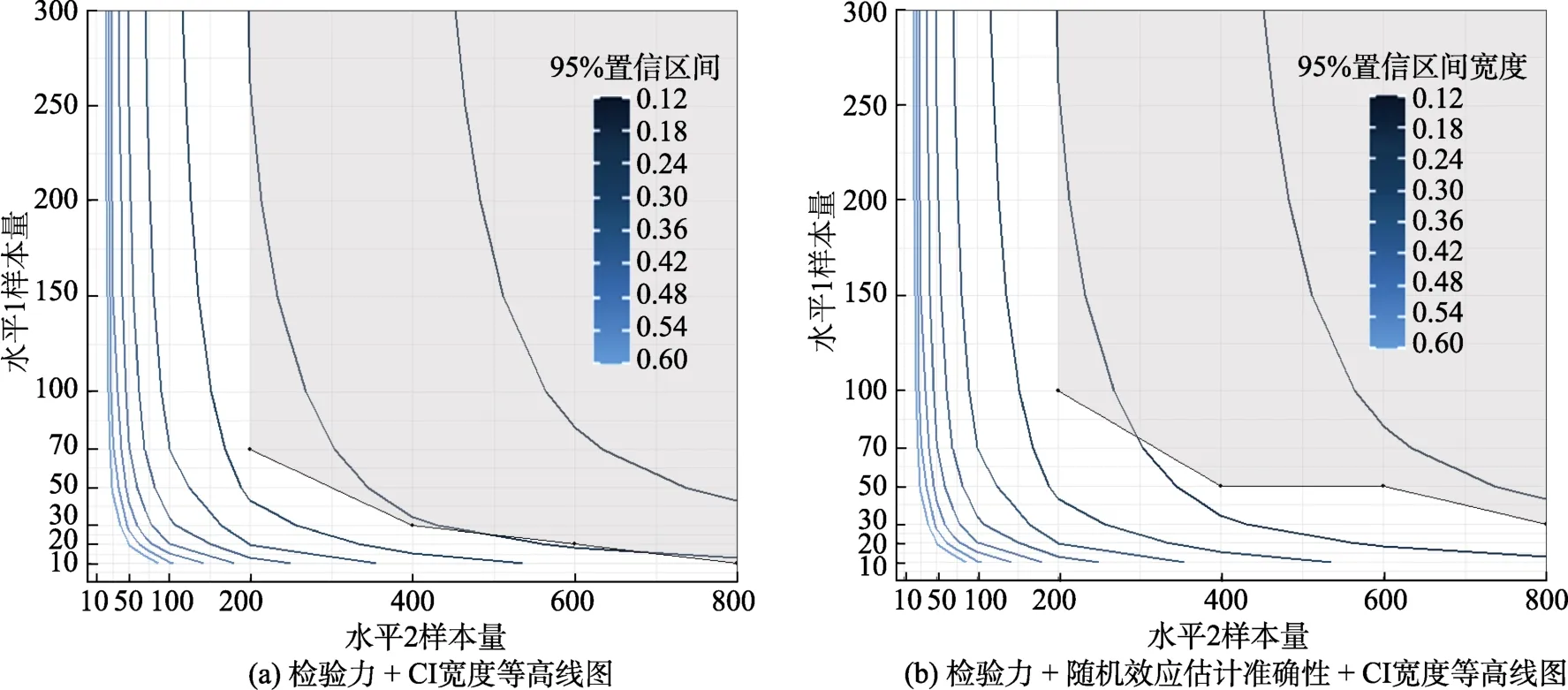
图3 研究2 平衡设计中等且 Wi 为分类变量时的CI 宽度等高线图

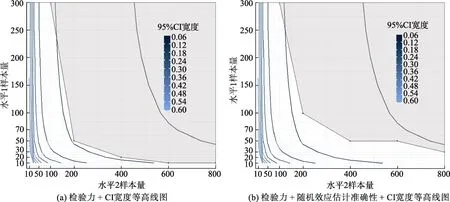
图4 研究1 平衡设计中等且 Wi 为连续变量时的CI 宽度等高线图

根据图3, 在满足检验力大于等于0.8 的标准的情况下, 如果95% CI 宽度小于等于0.18, 则推荐水平1 样本量 = 50, 水平2 样本量 = 400。在满足检验力大于等于0.8 且所有随机效应估计值rbias小于0.1 的情况下, 如果95% CI 宽度小于等于0.18,则推荐水平1 样本量 = 50, 水平2 样本量 = 400。根据图4, 在满足检验力大于等于0.8 的标准的情况下, 如果95% CI 宽度小于等于0.12, 则推荐水平1 样本量 = 50, 水平2 样本量 = 200。在满足检验力大于等于0.8 且所有随机效应估计值rbias 小于0.1 的情况下, 如果95% CI 宽度小于等于0.12, 则推荐水平1 样本量 = 100, 水平2 样本量 = 200, 或者水平1 样本量 = 50, 水平2 样本量 = 400。

平衡设计Wi为分类变量情况下,小和大的CI 宽度等高线图见附图4 和5 (在线补充材料1)。当小时, 阴影区域向右上移动, 满足要求的样本量增大; 当大时, 满足检验力要求的阴影区域略向下移动, 满足要求的水平1 样本量略减小,此时没有同时满足检验力大于等于0.8 且所有随机效应估计值rbias 小于0.1 的条件。

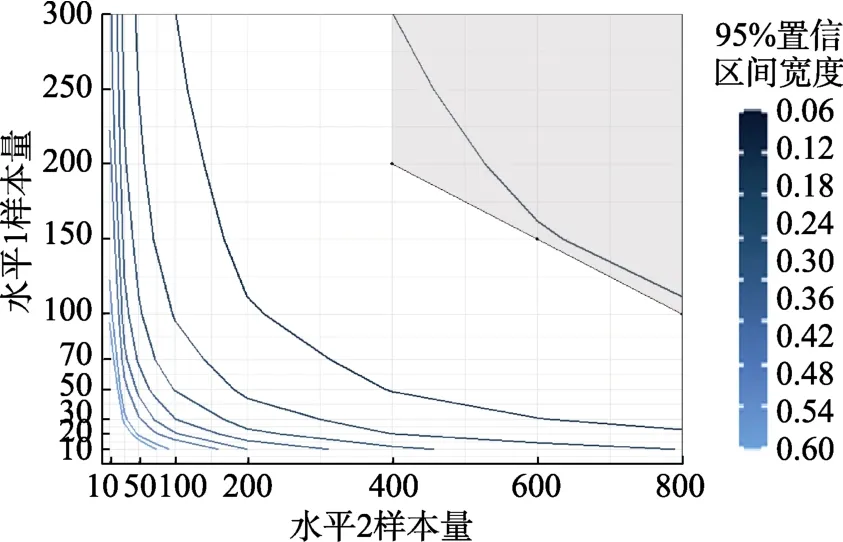
附图4 研究二平衡设计小且 Wi 为分类变量时的检验力 + CI 宽度等高线图

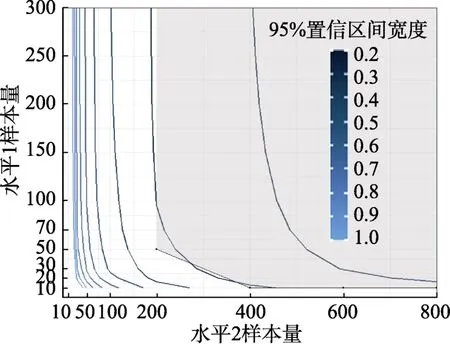
附图5 研究二平衡设计大且 Wi 为分类变量时的检验力 + CI 宽度等高线图

从附图6 (在线补充材料1)可以看出, 与平衡设计相比, 非平衡设计下的阴影区域向右方移动,说明满足要求的水平2 样本量增大, 至少为400 才能保证检验力符合要求。

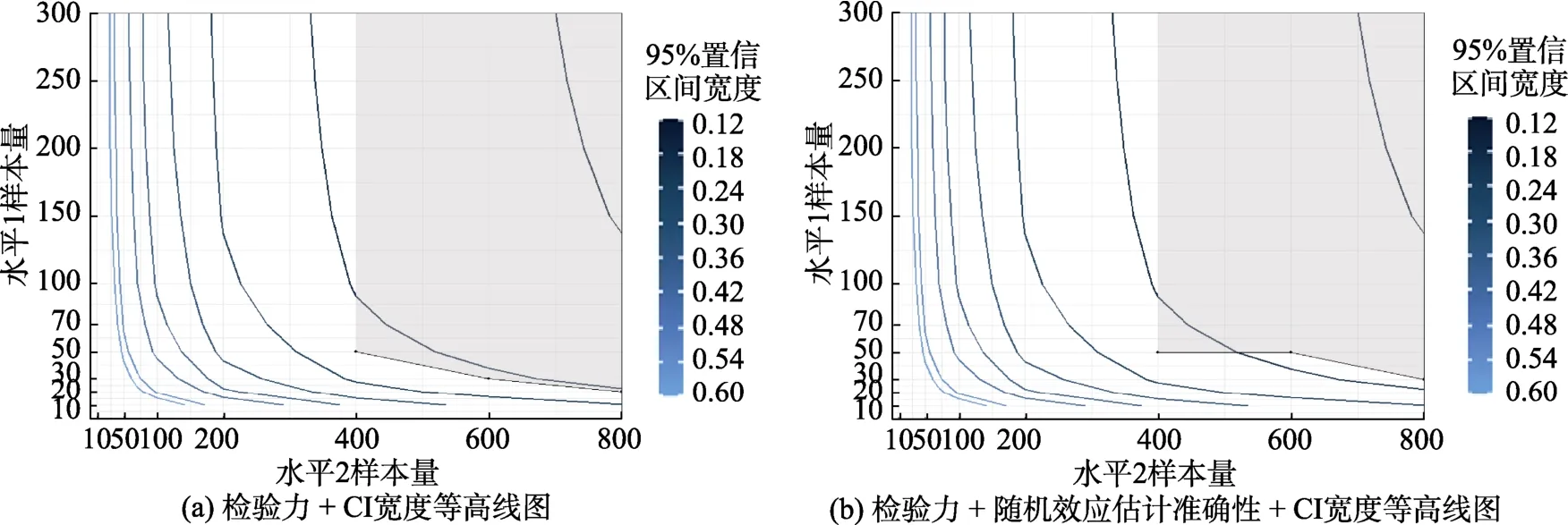
附图6 研究二非平衡设计中且 Wi 为分类变量时的CI 宽度等高线图

6 实例演示

本部分将通过一个例子, 说明在实际中如何运用本研究开发的函数生成CI 宽度等高线图, 指导样本量规划。

假设研究者想考察某些人格特征(如诚实、道德、幽默等)是否会影响其对异性的吸引力。可参考一项关于忠诚对异性吸引力影响的类似研究(Xu et al., 2020)。该研究采用刺激不重复的单因素被试内实验设计, 给被试依次呈现异性的头像, 同时附上描述他们在以往恋爱关系中是否忠诚的句子, 让被试对每个异性的吸引力程度等进行评分, 其中忠诚与否(忠诚、不忠诚)为被试内因素, 每个条件下有20 个不重复的刺激。研究结果显示, 表现出忠诚行为的潜在伴侣的吸引力评分显著高于不忠诚的潜在伴侣。研究者可以参考本文提出的方法开展样本量规划。

首先, 选取用于生成模拟数据的参数。采用借鉴前人类似研究结果设置参数。对于Xu 等(2020)的原始数据, 以是否忠诚为自变量, 以面孔吸引力评分为因变量(需标准化), 将数据与本研究模型1拟合, 估计参数。具体语句和结果请参见在线补充材料4。根据结果, 计算可得：。

然后, 设置参数, 调用函数, 生成评价指标结果和CI 等高线图。设定重复次数为N= 1000, 水平1 样本量包含6 个水平：40, 80, 120, 200, 300, 400。水平2 样本量包含6 个水平：10, 30, 50, 70, 100,200。自变量两个条件试次数相等。可接受的最宽95% CI 宽度为0.8 - 0.2 = 0.6。预设图中95% CI宽度的刻度为kd ＜- c (0.3, 0.4, 0.5, 0.6, 0.7, 0.8)。调用函数的语句如图5 所示。

最后, 运行程序得到评价结果文件“modelOne_evaluation_accuracy.csv”, 和检验力+CI 宽度等高线图(见图6)8由于本例中没有同时满足检验力大于等于0.8 并且所有随机效应估计值rbias 小于0.1 的条件, 因此无法生成检验力+随机效应估计准确性+CI 宽度等高线图。。根据图中所示, 在满足检验力大于等于0.8 的标准的情况下, 95% CI 宽度均小于等于0.6, 则最小的推荐样本量为：被试量为20 时, 共需要80 个试次; 被试量为30 时, 共需要60 个试次;被试量为70 时, 共需要40 个试次。

图6 实例演示检验力 + CI 宽度等高线图

7 讨论

7.1 主要研究结果

本研究针对线性混合效应模型, 采用模拟方法,以被试内实验效应和被试间变量的调节效应为例,实现基于检验力与效应量准确性分析的样本量规划。并通过两个模拟研究, 考察实验效应、随机斜率大小、被试变量类型和是否为平衡设计对样本量推荐结果的影响, 说明CI 宽度等高线图在样本量规划中应用。旨在为实践研究者基于具体研究实现样本量规划提供方法指导和便利工具。研究得到的主要结果如下。

第一, 从收敛情况来看, 对于模型1 来说, 基本不存在收敛问题。对于模型2 来说, 当随机斜率方差小时, 部分条件下会存在一定程度的不收敛问题。

第二, 从检验力来看, 效应量越大, 检验力越大。变量类型为分类变量时的检验力低于连续变量。平衡设计下的检验力普遍大于非平衡设计下的结果。此外, 检验力与样本量的关系还受所考察效应所属水平的影响。水平1 自变量效应的检验力主要受水平1 样本量影响, 水平2 自变量效应的检验力主要受水平2 样本量影响。两个水平的样本量具有一定程度的补偿作用, 增加关注效应所在水平的样本量能更好地补偿另一水平小样本量的问题。

第三, 从效应量及其标准误估计准确性来看,在拟合模型定义准确的情况下, 固定效应点估计值都较准确。但是, 其CI 宽度会受到是否为平衡设计和随机效应的影响。非平衡设计下的CI 普遍更宽。对于水平2 变量的调节效应, 随机斜率方差越大,CI 越宽, 效应量估计的标准误越大。各条件下效应量估计标准误的准确性都较高。

第四, 从随机效应估计准确性来看, 残差方差估计准确性都较高。随机截距和随机斜率方差估计准确性会受是否为平衡设计和随机斜率方差大小的影响。对于仅含被试内自变量的模型, 非平衡设计下随机截距方差和随机斜率方差的估计准确性更低。随机斜率方差越大, 随机截距方差的估计准确性越低, 随机斜率方差的估计准确性越高。随机斜率方差小时, 会高估随机斜率方差, 随机斜率方差大时, 会高估随机截距方差。

7.2 实践建议

本研究期望以两种较典型的线性混合效应模型为例, 说明规划样本量的方法。基于研究过程和结果, 提出以下建议。

首先, 样本量规划需同时结合检验力与效应量准确性分析结果。传统的样本量规划主要基于检验力分析展开(例如Schultzberg & Muthén, 2018), 确保推荐样本量能够满足检验力要求(0.8 及以上)。但是, 随着目前越来越多的学术期刊和研究机构呼吁在报告显著性的基础上, 报告效应量及其CI, 对效应量估计准确性的要求也日益受到重视(Maxwell et al., 2008)。其实, 基于检验力与基于CI 宽度规划样本量既有联系, 又有区别。两种方法的联系在于,无论是基于检验力还是CI 宽度规划样本量, 都与效应量的标准误有关。在固定效应模型下, CI 可以定义为[T- 1.96SE,T+ 1.96SE] (T表示效应量估计值,SE表示标准误)。在随机效应模型下, 随机效应的方差部分会加入到标准误的计算中, 因此, 与固定效应模型相比, 会得到更大的标准误(SE*), 此时效应量的CI [T-1.96SE*,T+ 1.96SE*]会更宽。无论是固定效应模型还是随机效应模型, 效应量的标准误越小, 效应量估计值的CI 就越窄, 效应量的估计值就越准确。在假设效应量不为0 的情况下, 越窄的 CI 就越不可能包括 0, 会得到更大的检验力(Cohn & Becker, 2003)。两种方法的区别在于, 真实的总体效应量越大, 其CI 就越不可能包括0, 因此检验力越大; 但CI 宽度不受影响。因此, 效应量越大, 基于检验力规划的样本量越小, 而基于CI 宽度规划的样本量不变, 这也与本研究结果一致。本研究发现, 基于检验力分析与效应量估计准确性推荐的样本量不一定相等。例如, 从研究1 的图2(b)中发现, 在水平1 自变量效应量中等的情况下, 当水平2 样本量为50 时, 水平1 只需要30 个试次, 就能保证检验力大于0.8。但此时实验效应的效应量估计值CI 宽度为0.7 左右, 大于可接受的最宽CI宽度。因此, 应当同时结合二者结果确定推荐的样本量。

其次, 在基于模拟方法进行样本量规划时, 应当谨慎确定产生数据模型的参数。通过检验力与效应量准确性分析开展样本量规划需要研究者预先设定一些模型参数(如预期效应量, ICC 等), 以便基于特定模型产生数据。特别说明的是, 本研究主要目的是说明样本量规划的方法及CI 等高线图的使用, 参数设置不一定代表实际中的大多数情况。在实际研究中, 研究者可以从前人已发表的类似研究,自己的预研究, 相关主题的元分析结果, 或者由同领域专家确定最小的重要效应来获得这些参数值(Pek & Park, 2019)。然而, 也有研究者指出, 这种直接使用效应量点估计值代替其真值(预期效应量)的方式忽略了其不确定性(uncertainty with regard to the unknown population effect size, Pek & Park,2019), 会得到有偏差的结果。因此, 一些研究者提倡使用考虑了不确定性问题的方法(如贝叶斯混合方法, Pek & Park, 2019)开展样本量规划。

然后, 实践研究者可以根据具体研究需要, 结合本研究提出的两种CI 宽度等高线图确定推荐的样本量。本研究参考Baker 等(2021)检验力等高线图的思路, 提出CI 宽度等高线图, 能够便于研究者同时参考多种要求, 找到最合适的样本量。研究者可根据实际研究对结果的要求, 确定选用某种CI宽度等高线图。如果研究者仅关注检验力和效应量估计的准确性, 可选用检验力+CI 宽度等高线图。如果研究者在此基础上, 还关注随机效应估计的准确性, 以便对个体差异的原因进行进一步分析(如应用混合效应均值——方差模型, Williams et al.,2021), 或者进一步准确计算包含随机效应的2R指标(例如Rights & Sterba, 2019), 可以选用检验力+随机效应估计准确性+CI 宽度等高线图。对于CI宽度, 研究者可以参考本研究的做法, 也可以参考前人研究中效应量的CI 宽度, 或结合自己研究中效应量报告精度的需要确定临界值。

最后, 在实际研究中, 样本量规划是结合检验力、效应量准确性与研究成本等的综合考虑。如果仅考虑检验力和效应量准确性, 往往会导致规划的样本量很大。较大的样本量会带来研究成本的显著增加。尤其是对于一些人力、物力成本较大的研究(例如, 应用功能性磁共振成像的研究等), 大幅增加被试量往往不现实。因此, 一些研究者提出了结合研究成本函数综合得到推荐样本量的方法(例如Baker et al., 2021), 以保证样本量既能够满足检验力等要求, 又使得研究成本尽可能最小。例如, 在Baker 等(2021)开发的网页中, 就结合了每名被试的成本, 计算推荐样本量。该网页中得到的推荐样本量是检验力达到80%且I× （J+成本 ）最小的点。除了研究成本, 在实际中不同研究确定样本量会结合不同的研究限制, 并有优先考虑的要求顺序等级。应用研究者可结合具体研究需求, 在本研究提供的方法基础上开展样本量规划。

7.3 未来研究展望

本研究具有一定的局限性, 未来研究可以从三个方面加以改进。首先, 本研究的模拟研究只考察了实验效应、随机斜率大小、被试变量类型、是否为平衡设计的影响, 很多因素设置为固定水平。未来研究可考察随机截距和随机斜率的协方差, 刺激的随机效应方差等因素对检验力和效应量准确性的影响, 获得更加丰富的结果。其次, 本研究以刺激嵌套于实验条件, 并且刺激和实验效应没有交互的被试内实验设计为例探讨样本量规划的问题, 并假设实验条件是含有两个类别的分类变量, 因变量是连续变量。未来研究可以拓展到其他类型的实验设计, 或者自变量为连续变量, 因变量为分类变量等情境, 探讨基于线性混合效应模型的样本量规划,丰富函数功能。最后, 本研究没有考虑预期效应量的不确定性问题, 不能反映实践中研究设计面临的现实困境。未来研究可以借鉴Pek 和Park(2019,2023)的思路, 通过检验力和效应量准确性的分布实现样本量规划。