运动员训练评估模型双值系数修正分析
李崇敏,潘道雍
(1.陕西国防工业职业技术学院 军事体育部,陕西 西安 710300;2.喀什大学 体育学院,新疆 喀什 844008)
近年来,国内运动员训练的研究集中于提升训练效果或安全保护方面。如基于虚拟现实技术的运动员模拟训练系统[1]、基于人工智能技术的运动员训练仿真模拟系统[2]等。我国运动员科学训练全面展开时间较晚,现阶段还没有准确而详细记载训练内容及综合结果的基本评估体系[3-5],不能实现深入解析,导致评估准确率较低。例如用改进的模糊层次分析法,结合定量与定性分析[6],但对指标权重矢量的确定主观性较强。结合运动员训练的数据集特征,对其训练综合效果进行评估,可以增加评估的参考基数,是当前的研究热点[7]。岳志强[8]提出基于马尔可夫模型的运动员训练效果评估方法,构建运动员体能训练效果评价的实证分析模型。曹瑾等[9]提出基于机器学习算法的运动员训练效果评估方法。但这些方法对评估指标权重的界定较为模糊,可能会对评估结果精度造成影响。因此,考虑到评估指标的权重,本文提出一种基于熵值法的差异熵值与差异权重双值系数修正的运动员训练效果综合评估模型。根据评估对象特征定义对应评语集,建立运动员训练综合评估模型。通过对差异熵值与差异权重的系数修正来确定指标权重值,使其更加符合评估规则,降低数据模糊性。将修正后确定的权重值代入综合评估模型中,得到最终评估结果,为运动员训练效果评估提供参考。
1 运动员训练评估模型建立
1.1 训练效果指标集和评估集建立
对于建立运动员训练评估模型,需要构建相应的指标集和评估集以便实施算法的具体研究,具体操作步骤如下:
(1)评估对象和指标集的建立。将评估对象设定为P,建立相应的指标数据集U表示为U={u1,u1,…,un},建立相应的评估数据集V表示为V={v1,v1,…,vn},其中n为固定常数。对指标集U中的每一个依据评语都进行模糊评判。
(2)建立评语数据集。设某评估等级为评语集(D),将所有运动员的训练结果用评语集D进行定义,D={优秀、良好、中等、及格、不及格},相应赋值为D={90~100、80~89、70~79、60~69、0~59},用于区分不同的评语等级,以及计算数据的综合评估结果。
(3)底层评估矩阵的建立。根据评估集(V),赋予每个指标数据的具体属性和评估等级进行评估,数值越大表明指标等级越佳。然后,将所有指标等级汇总并分析,得出最终综合训练评价矩阵R
其中,rnv表示对矩阵最底层中第n个数据指标的评估。
1.2 训练效果综合评估
对于评估数据集V、指标数据集U及评语集D共同组成的训练效果综合评估模型,将评估对象P进行综合评价的目标向量设为W,表达式为
其中,W表示各项训练指标的目标权重向量,R表示评价矩阵。
为使评估结果更具真实性和严谨性,需采用加权评分原则对全部综合结果进行评分。设该加权评分集为V=(v1,v2,…,vn),将评分等级与实际训练评估的向量值进行综合计算,得出
其中,Z表示综合评估结果,qi表示评估对象p在整个数据集上对第j个评价等级的表达隶属度。综合上述过程,根据实际训练情况对所有数据进行完整的综合评估。
2 基于双值系数修正的指标权重值确定
在运动员训练效果评估模型基础上,采用熵值法估算指标权重,即指标信息的差异系数[10-11]。差异系数越高表明对评价的重要性越大,即权重越大,对评估结果的贡献越大。同时,为保持序列平衡,本文对差异熵值系数及差异权重系数进行修正,以优化指标权重值的结果进而优化评估模型的结果,以下为具体过程。
以上述建立的评估对象、评语集、评估集以及评估矩阵为基础,通过分别赋予不同权重数值的方式修正原始数据。首先,设在全部数据集中有m个关于训练结果的评估权重序列以及n个数值评估指标,在i个评估权重序列中与其对应的第j个权重数值就可表示为xij,基于此,得出权重评估矩阵
对X施数值标准化后,得到归一化的标准矩阵
在同一数据指标下,对样本数据集进行权重序列分布的具体比重pij为
在j个数据指标下信息熵ej的表达式为
可以看出,对于第j个数据评估指标,m值越大,该指标数值的差异性越大。需要对其进行简化权重操作,保证序列的平衡。将数据集的差异熵值系数设定为ϖ,差异权重系数设定为gj,在此关系下第j个评估指标下的表达式为
其中,ϖj代表第j个评估指标下的差异熵值系数;gj代表第j个评估指标下的差异权重系数。对差异熵值系数ϖj以及差异权重系数gj进行修正,得到
评估模型的指标权重双值系数修正完成,将修正后的权重代入训练效果综合评估模型中,得到最终的综合评估结果。
3 仿真实验
3.1 实例分析
3.1.1 实验环境 采用某体育院校2019 级5 组国家二级运动员的10 组时长为45 分钟的训练项目作为实验样本数据。训练样本集中包含评估所需的指标项目,分别有1 项体能训练、1 项专业知识训练、2 项实操训练及1 项综合答题测试项目。
除知识训练成绩、综合答题测试成绩及实操训练成绩的记录外,为更好地量化与可视化运动训练的效果,体能训练时的体能数据采集通过心率系统软件进行。实时采集各项运动数据,包括监测心率、卡路里与运动强度等,同时判断体能训练的负荷强度,避免实验对象运动不足或过度,保证实验的有效性。
3.1.2 评估矩阵计算结果 5 种项目评估数据表示为r1、r2、r3、r4、r5,由此组成的综合评估集R=[r1,r2,r3,r4,r5],综 合 结 果 的 评 语 集D=[d1,d2,d3,d4,d5]。对 应 的 具 体 评 价 等 级 和 分 数 值 见1.1 部 分。2019 级5 组班级的实际训练平均分数为82.986。
通过本文建立的数据评估模型对实验样本进行综合评估结果计算,得出的评价矩阵为
基于双值系数修正的熵值法计算得出最终综合训练评估结果见表1。
以此计算得出的训练结果综合评估分数为Z=82.114,与评价集中的等级参考对照,表明该校2019 级的5 组二级运动员的综合训练效果良好,可以判定原始数据基本无误,准确率较高。
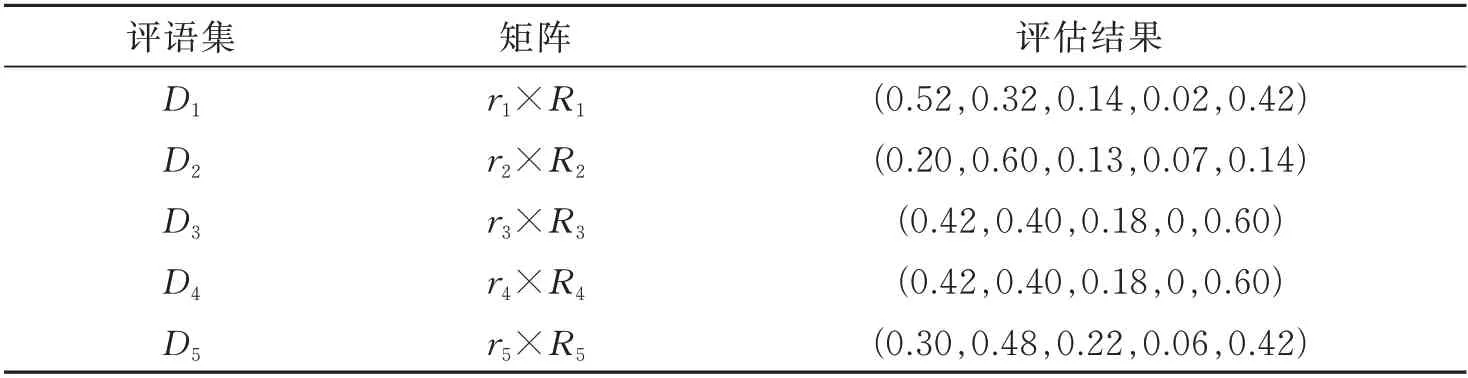
表1 最终综合训练评估结果Tab.1 Final comprehensive training evaluation results
3.1.3 基于偏差熵值的评估结果分析 综合评分后还需进一步确定实验样本的评估偏差熵值的等级,根据文中的计算方法得出基于最终的评估熵值。评估熵值越大,等级判定误差越小,具体结果如图1 所示。
从图1 可以看出,五个评价等级曲线表现良好,浮动状态稳定,整体保持在0.5~1.0 的范围内,本文各指标等级曲线与原始数据曲线变化幅度基本保持一致,融合性较强,在任意取值区间内进行分段对比,二者曲线的一致性都较高,说明本文方法的综合评估效果与原始数据的对应率较高、准确性较强,曲线基本没有出现高峰值或低峰值现象。
3.2 模型对比分析
为进一步验证所设计运动员训练评估模型的有效性,与文献[8]和[9]的方法对照,分别对实验样本进行训练效果评估。
3.2.1 评价指标 为评价模型评估精度,选取平均绝对误差M、决定系数F以及平均绝对百分比误差A作为评价指标。计算公式为

图1 2019 级5 组班级的等级评估熵值Fig.1 Grade evaluation entropy of 5 classes in 2019
其中,N为评估样本的总个数,Xi代表实际评估数值,xi为模型评估预测值,xˉ为均值。当M与A数值越小,模型评估预测的误差越小,模型的拟合效果即评估精度越佳;而F数值越大,模型评估精度越高。
运动员训练效果评估模型的可靠性通过总计相关性与α系数来反映。总计相关性是分析项之间的相关系数,反映了单个评价指标项目与其他评价指标项目之间的相关关系。α系数检验模型的信度,评估模型单独执行的可靠性。
为验证运动员训练效果评估模型的评估效率,设评估效率系数为E,计算公式为E=-(cm2Δt)。其中,c为运动员训练数据嵌入训练效果评估模型的比特数值,m为运动员训练效果评估的失真度,Δt为效果评估的评价指标因子统计值。评估效率系数值越高,表示评估效率越高。
3.2.2 评估精度对比分析 以3∶7 的比例设置训练集与测试集。本文方法、基于马尔科夫模型的文献[8]方法与基于机器学习算法的文献[9]方法的训练效果,评估结果如图2 所示。
从图2 可以看出,在不同的评估模型对运动员训练效果进行评估预测时,本方法M与A值是最小,对于不同的实验次数,平均值M与A分别为1.17% 与9.26%;本文算法的F值是最大的,平均值为0.941。本方法的评估精度更高,评估效果更佳。而改进修正了熵值法的差异熵值与差异权重双值系数的评估模型更具优势。
3.2.3 评估可靠性分析 通过统计软件SPSS 20.0 计算本方法与文献[8]和[9]的方法总计相关性与α系数值,对比不同评估模型的可靠性,结果如图3 所示。
由图3 可知,本方法的评估总计相关性与可靠性系数均高于其他评估方法。在不同实验次数下,本方法的平均总计相关性为0.942,平均α系数值0.935;文献[8]和[9]方法的平均总计相关性分别为0.851、0.737,平均α系数值分别为0.836、0.694。说明本模型得到的评估结果可靠性和可信度更高,有利于为运动员训练效果的提升提供数据支持。

图2 不同方法评估精度对比Fig.2 Comparison of evaluation accuracy of different methods
3.2.4 评估效率对比分析 采集5 组训练实验对象的实验数据,对本方法与文献[8]和[9] 的方法进行评估效率对比实验,结果如图4 所示。
从图4 可以看出,计算不同方法的评估效率系数E,得到不同方法的评估效率。针对不同组别的训练对象的训练数据,本文方法的评估效率分 别 为 89.91%、87.96%、93.73%、95.14%、90.82%。与文献[8]方法和文献[9]方法相比,本文方法对于训练效果的评估效率明显更高一些。反映了获得的运动员训练数据在所研究的训练效果评估模型中的拟合嵌入度较高,相比对照方法来讲更具有评估适应性即评估优势。
4 结论

图3 不同方法评估可靠度对比Fig.3 Comparison of reliability evaluation of different methods
对于训练效果的综合评估一直是运动员训练中的重点及难点问题,本文通过对评估指标的权重改进实现对所有数据的有效评估。构建相应的指标集和评估集,方便评估模型的实施,并通过分别对其赋予不同权重数值来修正原始数据,利用差异熵值与差异权重的双值系数修正保证训练评估的准确度。仿真实验证明,本文方法可以实现高效的数据评估,与原始数据的匹配度、精准度较高,评估效率系数较高,训练评估优势更为突出。
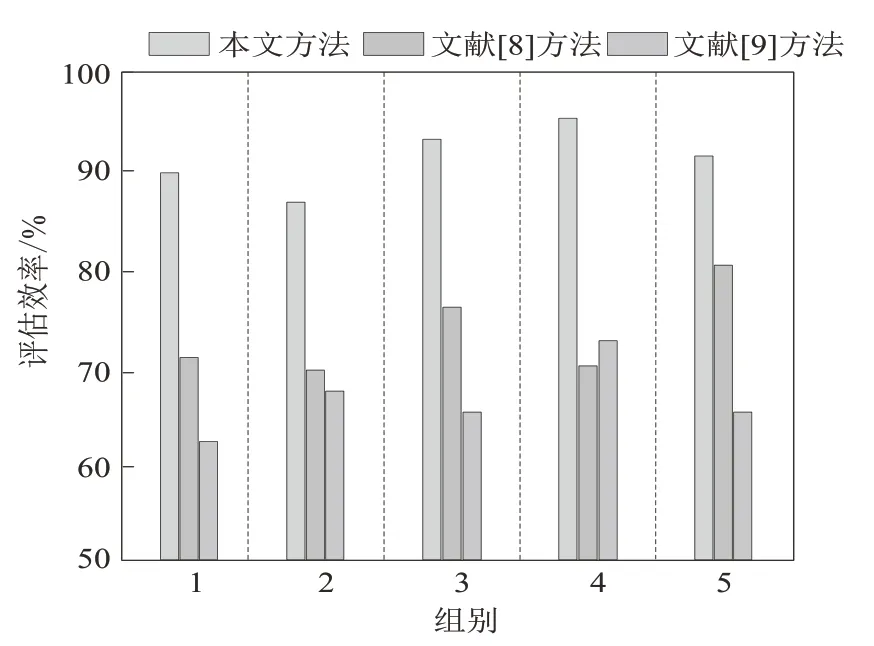
图4 不同方法评估效率对比Fig.4 Comparison of evaluation efficiency of different methods

