基于多体动力学模型的柴油机曲轴振动特性分析

彭凌溥，柴子涵，金志浩

（沈阳化工大学 机械与动力工程学院，辽宁 沈阳）

引言

柴油机的曲轴系统的受力十分复杂，是由往复运动惯性力和燃烧压力最大时的转动惯性力以及曲轴系统的激振力等组成的。因此对曲轴系统的扭振分析是一个十分复杂的过程，过去一般建立一个等效离散系统模型，然后对模型在进行简化分析，但是其中的误差很大。建立一个和实体三维模型这样就避免了简化所产生的误差，而且动力学仿真更加直观的计算出实际的激振力。发动机曲轴系统的激振力会引发曲轴扭振，会通过动力传输路线传递给其他构件。以上所提到的就是该多体动力学仿真方法与其他计算方法相比的优点。

Zeischka[1]使用了曲轴和发动机缸体的多体弹性动力学模型，模型使用了有限元模型，随后被导入整体四缸发动机模型，包括连杆和活塞的刚体表示。流体动力学轴颈效应通过阻抗方法实现。阻抗图提供了轴颈力与轴承尺寸、油粘度和偏心率等参数的函数关系。

郭一鸣[2]提出了一个详细的单缸内燃机多体数值非线性动力学模型。该模型结合了发动机部件的大位移动力学、支撑轴承的无限小振动和截留空气力燃料气缸瞬态压力的同步求解。获得的结果提供了所有惯性构件（如活塞、飞轮和连杆）的动态响应的时间历程，还获得了曲轴的扭转振动以及轴颈轴承的同步和异步旋转。

戴成[3]讨论了如何将多体动力学与柔性体效应相结合，以预测轴承载荷、曲轴振动、每个轴颈的轨迹图以及由于结构柔性而产生的轴承性能。滑动轴承中的油膜效应采用阻抗法和流体动力油膜结合有限元法来实现。以一台V6 发动机为例，说明了柔性系统和滑动轴承载荷的动态响应。

杨鑫[4]提出了一个4 缸4 冲程柴油发动机的多体模型，结合了部件的灵活性。该模型还包括发动机点火顺序和实验测量的燃烧时间历程，以提供由于柔性曲轴系统的组合扭转- 偏转模式引起的飞轮锥形运动的数值预测，这种振动响应的数值预测与实验结果符合得很好。

现代仿真方法是以实体模型为基础，利用柴油机示能图加载激磁力矩，并考虑曲轴轴承支承力、轴系与机体的耦合作用，使柴油机曲轴系统扭振计算接近实际工况，有利于获得准确的计算结果。本文采用UG建立了某型重型柴油机曲轴系统的三维模型，该系统由曲轴、活塞、连杆、飞轮和硅油阻尼器组成。并利用ADAMS 建立刚柔耦合的轴系多体动力学模型，将柴油机曲轴转化为柔性体。曲轴的轻微变形可以保证具有变形广义坐标一阶项的动力学方程的完整精度。

1 曲轴系统装配模型

根据某型重型汽车柴油机轴系零件及装配图，建立由曲轴、活塞、连杆、曲柄销、飞轮、硅油阻尼器等模型零件组成的曲轴系统，运用三维建模软件UG，然后组装起来如图1 所示。

图1 柴油机轴系动力学模型

由于飞轮的质量和转动惯量很大，相对于测功机和柴油机而言。柴油机台架试验采用柔性连接，限制了扭振对曲轴系统的影响。因此在动力响应分析仿真中，刚柔混合多体系统不考虑测功机和弹性联轴器部件。基于上述模型求解系统的动态响应，得到系统动态响应的时程，计算分析系统的扭振响应。

1.1 曲轴系统动力学模型

用UG 将曲轴系统模型装配完成后导入ADAMS,然后建立约束模型如图1 所示。

硅油阻尼器造型：外壳与曲轴之间建立固定连接，惯性块与外壳之间增加旋转连接，惯性块与外壳之间增加扭簧连接。

1.2 曲轴多体动力学模型

在软件ADAMS/Auto Flex 模块中先在曲轴表面划分大小为10 mm 的网格，然后用“Find Attachments”将曲轴周围的连接点找出来连接附近的节点。

自动构建曲轴柔性体替代原有刚体，并在连接点施加约束力。我们可以在柔性曲轴特性中查看曲轴的各个振动模态，前1-6 模态频率很小，接近于零，可以舍弃。前十自由模态的柔性曲轴如图2 所示。

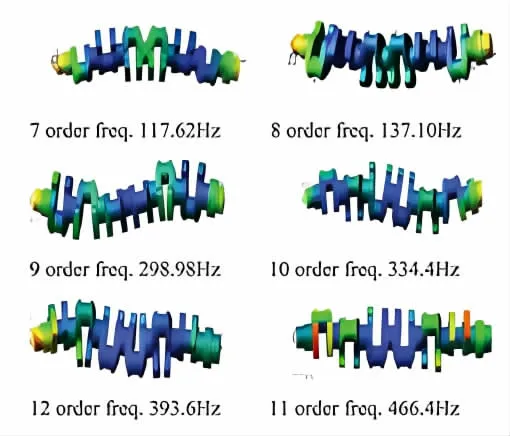
图2 ADAMS 刚柔耦合柴油机轴系多体模型图

1.3 硅油阻尼器动态模型

硅油阻尼器主要通过阻尼部分（惯性块）和驱动部分（外壳）来实现减振，其机械模型简图可简化为图3。

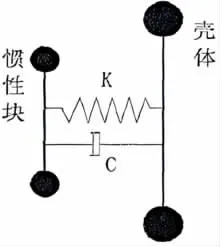
图3 硅油阻尼器的机械模型

将硅油视为纯粘性流体，仅表现阻尼作用，弹性系数k=0，用工作过程动平衡法计算各转速对应的阻尼器系数。

2 柴油机轴系主要负荷

2.1 柴油机示功图

通过柴油机台架试验，按图4 所示外特性曲线施加负载，测量各转速点（800、900、1 000、1 100、1 200、1 300、1 400、1 500、1 600、1 700）的转速对应的指示图(曲轴转角1 度时各缸气压)如图5 所示为转速为1 900 rpm。

图4 柴油机外特性曲线

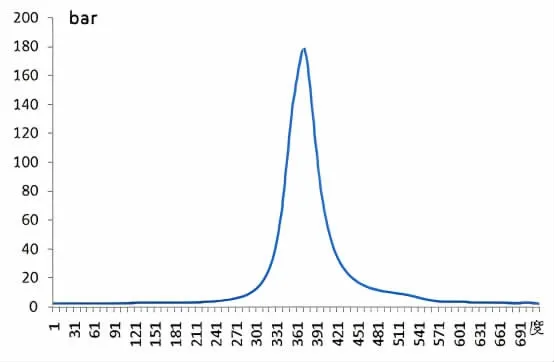
图5 柴油机转速（1 900 r/min）示功图

2.2 施加轴系载荷

气缸内压力与活塞端面积的乘积得到活塞上的载荷。6 缸负荷大小基本相同，只是各缸峰值时间不一样，由ADAMS 中的函数AKISPL 插值法得到压力。6缸顶部承受的载荷力如图6 所示。

3 仿真结果

该柴油机工作转速范围为800～2 100 r/min，计算转速区间为100 r/min，模拟了曲轴系统的扭振，提取了曲轴自由端的瞬时转速信号数据。首先减去平均速度得到瞬时速度差，然后是扭振得到曲轴系统自由端的响应（扭角），进行FFT，得到扭角幅值。

选取1 700 r/min 转速、3 000 步/秒下的仿真数据，通过该仿真得到曲轴自由端（硅油阻尼器安装在曲轴上）的瞬时转速和扭矩，数据曲线如图7～9 所示。

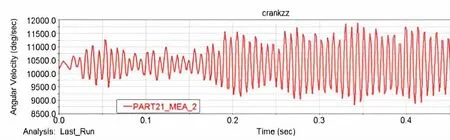
图7 曲轴自由端的瞬态角速度图

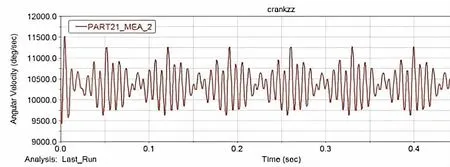
图8 自由端瞬态角速度与平均角速度的差异图

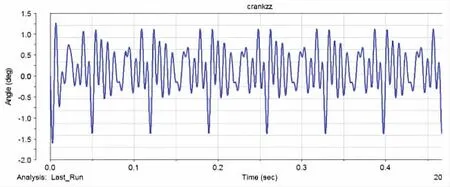
图9 瞬态曲轴自由端角的积分图

当转速为1 700 r/min 时，6 次谐波频率为170 Hz。从图10 得出曲轴自由端的扭转角为156 度。对于本文分析的6 缸柴油机，可能引起曲轴危险共振的发动机干扰转矩为3、4、6 次谐波。其中，6 次谐波的扭振幅值最大。

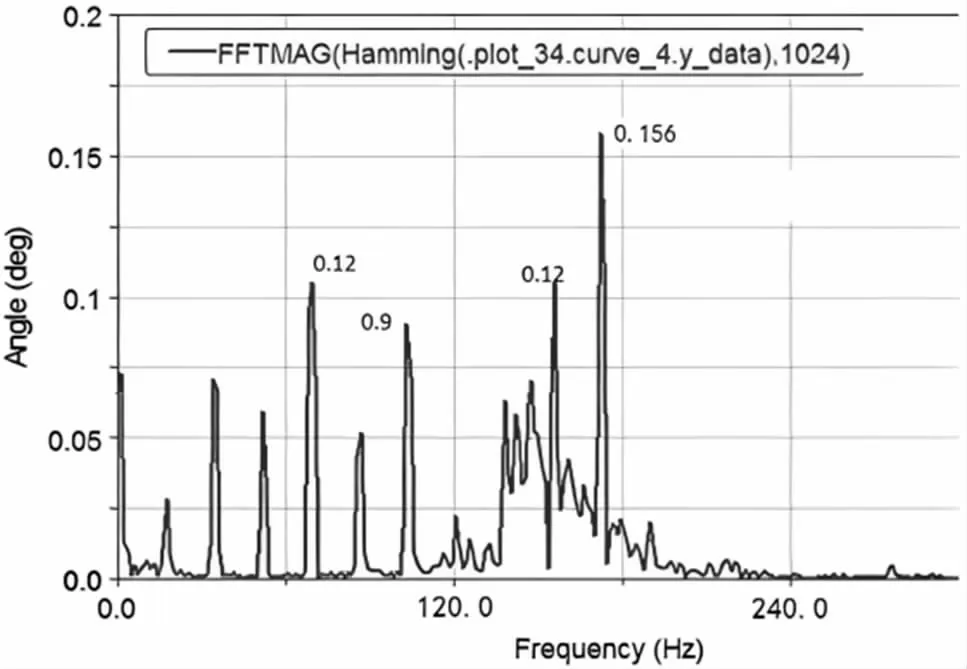
图10 曲轴自由端扭转振动角值的频谱图

该柴油机800～2 100 r/min、各转速间隔100 r/min 的仿真结果采用相同的方法进行计算，根据曲轴对应的转速，曲轴自由端6 次谐波扭转角的幅值将系统提取出来，绘制出曲轴系统自由端的6次谐波扭矩- 转角曲线，如图11 所示。曲轴系统自由端扭转角的最大幅度为0.16 度，共振速度约为1 800 转/分。

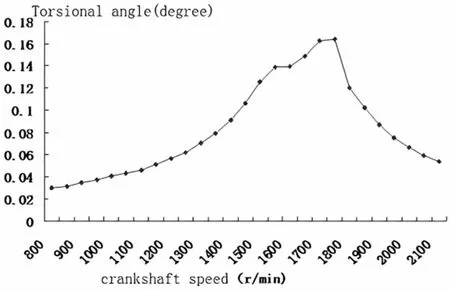
图11 轴系统自由端的扭转角

4 结论

利用多体动力学研究了曲轴系统扭转振动研究的一般方法和步骤。通过ADAMS 对纯粘性硅油阻尼器幂律流体的力学模型和多体动力学模型进行仿真分析。

得出的结论有：当柴油机装上与之相应的硅油阻尼器运行时，轴系扭振明显减小，主谐波最大扭转角(6 次谐波）从0.54 降低到0.16，阻尼效果非常明显。

通过多体动力学仿真得到轴系的扭振幅值和共振转速，与实际试验结果接近，仿真计算具有较高的精度和应用价值。