基于改良和声搜索的电力系统动态经济调度
齐红伟*,邹德旋
(江苏师范大学 电气工程及自动化学院,江苏 徐州)
引言
随着社会经济的快速发展,居民用电和工业用电不断大幅提升,各地出现不同程度的供电紧张情况,电力系统动态经济调度(Dynamic economic dispatch,DED)重要性日益凸显。DED 是在规定的调度时段内,在满足一定约束条件下,规划调配发电机组的输出功率,以使电力系统在发电成本最低的状态下运行。
DED 是电力系统优化极其重要的组成部分,在优化过程中要考虑不同区域之间的联络线容量、上下限发电极限、发电机斜坡速率、传输损耗、阀点效应、禁区运行区(Prohibited Operation Zone,POZ)、燃料成份比等等约束条件,在满足运行负荷条件下,发电机组以最经济方式运行。
目前已有的多种算法,分别从不同方面对各种约束条件进行了优化。
针对能源方面,有使用准对偶群搜索优化方法[1];有从阀点效应的角度考虑,提出自适应回溯搜索优化算法[2]、将蜂群优化与序列二次规划相结合的混合方法[3]、基于改进模式搜索法的算法[4]、增强的探索性鲸鱼优化算法[5];有从斜坡速率限制角度考虑,用传统的lambda 迭代技术进行测试,然后将结果用于训练基于Levenberg-Marquardt 算法(LMA)的人工神经网络[6]。
上述文献虽然分别提出了各种解决方法,但多种约束条件考虑不够完全。为了进一步降低DED 问题中的发电成本,本文提出一种基于改良和声搜索算法(Reformed harmony search, RHS)。该算法适用于不同约束条件下的DED 问题,具有较强的问题适应性。
1 问题描述
发电机组DED 包括目标函数和约束条件2 个部分。
1.1 目标函数
目标函数表示为公式(1):
公式(1)中,fc表示整个调度周期内总的燃料成本;Pn,t表示电力机组n 在时段t 的输出功率;N 表示发电机组的总数;T 是调度时段总数;C(Pn,t)表示产生输出功率Pn,t所消耗的燃料成本,在不考虑阀点效应的情况下,C(Pn,t)表达为公式(2):
公式(2)中,an、bn、cn为发电机组n 的燃料成本系数。
考虑阀点效应的DED 目标函数要复杂一点,多了正弦函数部分,此时C(Pn,t)表达为公式(3):
公式(3)中,an、bn、cn为机组n 的燃料成本系数;dn和en为机组n 的阀点效应系数;Pminn为发电机组n 输出功率的最低容限值。
1.2 约束条件
总的燃料成本受到多种约束条件的限制,主要包括输出功率容限、输出功率变化率、功率供需平衡等。
(1) 输出功率容限约束
(2) 输出功率变化率约束
公式(5)和(6)中,URn是第n 台发电机组的上升容限值;DRn是第n 台发电机组的下降容限值,此约束限制为每台发电机组发电的变化范围,变化值需要符合要求。t =2, …, T ;n =1, …,N。
(3) 功率供需平衡约束
2 改良和声搜索算法
和声搜索(Harmony search, HS)算法是一种性能良好的优化算法,已在多个领域获得较好的应用。为了能在求解DED 问题时获得更优的解,需要对和声搜索算法的步骤进行调整。基于上述考虑,本文提出了一种改良和声搜索算法(Reformed harmony search,RHS)。RHS 改进了和声记忆考虑步骤,排除了随机化步骤。具体来说,RHS 的整个流程描述如下:
(1) 初始化问题参数,如变量数目D,变量上限Xd,U和下限Xd,L(d=1,…,D),成本系数,时段数目,各时段电负荷,禁止运行区。
(2) 初始化控制参数,如和声记忆规模(Harmony memory size, HMS)、初始基音调整概率(Pitch adjusting rate, PAR),迭代次数,混沌序列初始值。
(3) 执行和声记忆考虑步骤。
对于每个变量,利用公式(8)获得混沌随机数:
公式(8)中,r 为混沌序列随机数;ζ 为混沌序列系数,这里设置为4,这样能始终保证随机数r 在[0,1]内。图1 给出了经过100 次(次数可根据计算需要进行调整)获得的混沌序列随机数的仿真图,可见该随机数始终位于[0,1]内,但与均匀分布的随机数不同,该随机数为非均匀分布。
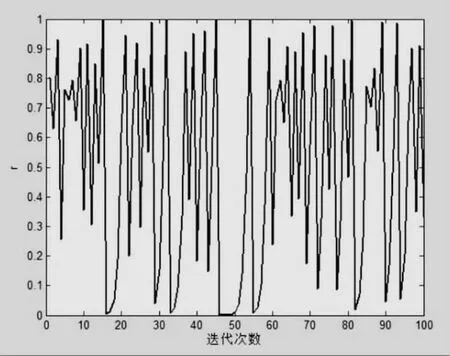
图1 基于混沌序列的随机数
基于该随机数,即可获得动态基音调整概率,表示为公式(9):
公式(9)中,PAR0为初始基音调整概率;PAR 为动态基音调整概率。当随机数较小时,PAR 也相对较小,此时有利于算法进行局部寻优;当随机数较大时,PAR也相对较大,此时有利于算法进行全局寻优。
另外,RHS 采用了一种动态基音调整步长,表示为公式(10):
公式(10)中,yd为当前和声记忆库中第d 维变量最大值与最小值间的差值。因为和声记忆库在每次迭代中都要更新,因此基音调整步长是随着迭代次数的增加而不断变化,有利于维护种群多样性。
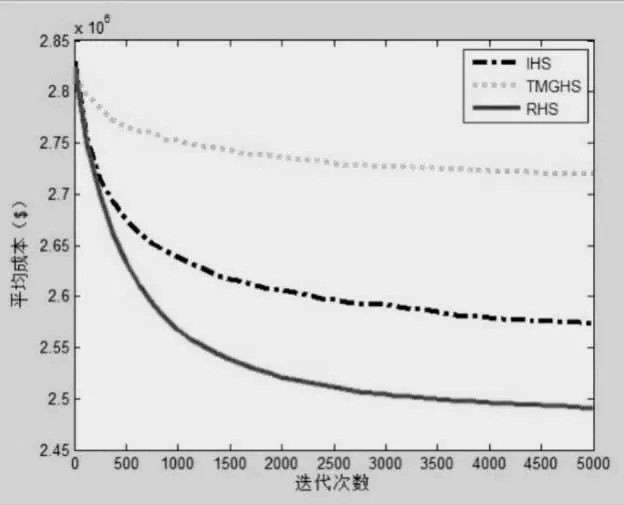
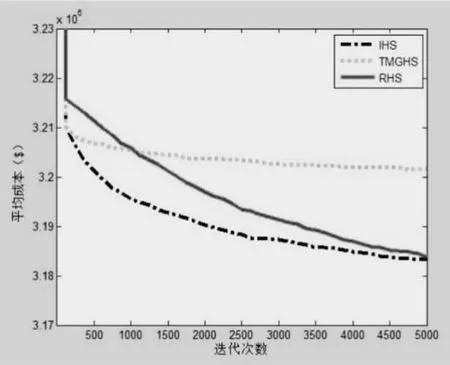
当rand() 公式(11)中,xnew,d为新和声向量xnew的第d 维变量;xi,d为第i 个和声向量xi的第d 维变量,且i^为[1,HMS]内的一个随机索引。 (4) 执行全局搜索步骤。 本全局搜索步骤利用全局最优和声向量xbest对新和声向量xnew进行更新,相应的更新公式表示为公式(12): 公式(12)中,xbest,d为全局最优和声向量的第d 维变量。该全局搜索步骤驱动当前和声向量向全局最优和声向量移动,有益于提升自身的质量。 (5) 判断是否满足终止条件。 若当前迭代次数达到了预设的最大迭代次数,则停止迭代,否则继续迭代。 综上,RHS 算法完整流程如图2 所示。 图2 RHS 算法流程 本文求解三个不带禁止运行区的DED 问题,分别为5 单元(问题1)、10 单元(问题2)和30 单元(问题3)电力系统动态经济调度问题,它们的问题数据可参照文献[7]。使用三种改进和声搜索算法对这三个问题进行求解,三种算法的控制参数设置如下:对于改进和声搜索算法(Improved harmony search, IHS)[8],和声记忆考虑概率为0.9,最大、最小基音调整概率分别为0.99 和0.01,最大、最小基音调整步长分别为公式(13)和公式(14): 对于基于趋向移动的全局和声搜索算法(Trending mobile global harmony search, TMGHS)[9],和声记忆考虑概率为0.4,变异率0.005,步长缩减因子0.2。对于RHS 算法,初始混沌序列为[0,1]内的随机数,混沌序列系数设置为4。公平起见,每种改进和声搜索算法的和声记忆规模都设置为20,迭代次数都设置为5000。对于每个DED 问题,三种改进和声搜索算法都独立运行30 轮。运用Matlab 软件对问题及算法进行编程,所获得的实验结果如表1 所示。 表1 三种改进和声搜索算法求解问题1、2、3 的优化结果 表1 给出了三种改进和声搜索算法求解问题1、2、3 的优化结果。由表1 可知,本文提出的RHS 算法获得的三个问题的平均优化时间都是最小的,RHS 获得的最小值、最大值和平均值也是最小的。说明该算法具有最快的计算速度,能够获得更高质量的解。 图3、图4、图5 给出了三种算法求解问题1、2、3时的进化曲线。可以看出,对于问题1 和问题2,RHS算法的平均成本曲线从优化初期就处于较低水平,且其相对于其他两种算法的优势保持到迭代末期。对于问题3,IHS 算法的进化曲线在整个迭代过程中处于较低水平,而RHS 算法的进化曲线随着迭代的增加快速下降,最终下降到与IHS 算法的进化曲线相近的水平。总之,RHS 算法具有较强的收敛性,其进化曲线随着迭代次数的增加而稳步下降,最终收敛到最低的平均成本水平。 图3 三种算法求解问题1 时的进化曲线 图4 三种算法求解问题2 时的进化曲线 图5 三种算法求解问题3 时的进化曲线 DED 问题含有较多的变量和约束条件,且具有非线性的属性,因此求解难度较大。为了获得该问题的理想解,本文提出一种基于修正和声记忆考虑步骤与全局搜索步骤的RHS 算法。RHS、IHS 和TMGHS 被同时用于求解3 个DED 问题,对于每个问题,三种算法都独立运行30 轮。根据实验结果,RHS 在求解任何一个问题时都能获得最小的平均运行时间、最低成本、最高成本以及平均成本,说明其的优化效率要高于其他两种和声搜索算法。总之,RHS 能在短时间内获得高质量的解,有益于节省电力系统的发电成本,提升其经济收益。
3 实验及分析


4 结论

