AR 策略对强遮挡北斗监测站精度影响研究

许运习

（中国铁路上海局集团有限公司合肥铁路枢纽工程建设指挥部，安徽 合肥）

引言

自国内启用北斗导航定位系统（Beidou Navigation Satellite System，BDS）以来，其在各行各业的影响已日益明显。与其他导航系统相比，北斗因其抗遮挡特性、共视卫星数量及广泛的信号频段而在定位精度上有显著优势。在诸如铁路、桥梁等基础建设项目的变形监测中，北斗监测站凭借其全天候、低成本、高精度特点，已成为首选测量工具[1]。但遮挡环境中的多路径效应对观测精度有负面影响。传统多路径改正方法在大规模应用中面临挑战。为提高遮挡环境的定位精度，深入研究模糊度固定策略（Ambiguity Resolution，AR）是关键，其将助力更精确的残差获得，满足监测工程需求。后续将基于RTKLIB 探讨不同模糊度固定方法及其效益。

1 LAMBDA 搜索原理

在地面监测站的卫星观测过程中，北斗系统普遍采用载波相位测量法。其中，特别关注的是B1 频段信号，最为常用的载波信号频率达到1 575.42 MHZ。该频段的信号当中，相同的整周模糊度在载波相位信号中一直存在。为了实现精确的定位，确定载波相位的整周模糊度成为了首要任务。

核心的问题在于如何固定或确定这一模糊度。正因为此，GNSS 中的模糊度固定步骤被视为高精度定位的关键环节。而在多种尝试和研究中，Teunissen 教授所提出的整数最小二乘模糊度降相关平差法（LAMBDA）脱颖而出，被认为是目前效果最佳的技术路径[2-3]。

LAMBDA 的工作原理融合了整数降相关技术与最小二乘技术。其核心是在进行模糊度参数间的多维整数变换后，减少了相关性，为进一步的整数搜索创造了条件。之后，通过整数搜索完成固定，再将搜索结果转化回模糊度的原始空间。不可忽视的是，本研究的核心工具RTKLIB，就选择了LAMBDA 作为其主要的模糊度固定策略。

因为不同模糊度之间存在互相关联，当一个模糊度参数发生变化时，会对其他模糊度的搜寻产生影响，从而增加搜索算法的复杂度。如果我们能够减少模糊度参数间的关联性，即一个模糊度的改变对其他模糊度的影响较小，那么可以有效地提高模糊度搜寻的速度。LAMBDA 算法是通过对模糊度参数及其方差- 协方差矩阵执行整数高斯转换（也可称作z 转换），从原始空间转移到新的空间，从而达到降低模糊度之间的相关性的目的[4-5]。

在此公式里，N、N0、QN是原始空间里的实数模糊度、整数模糊度和方差- 协方差矩阵。而、、QN则代表新空间里的实数模糊度、整数模糊度和方差- 协方差矩阵。其中的矩阵每个元素都是整数，且其行列式的绝对值为1；这一矩阵的逆也完全由整数构成，而z 包括众多整数转换的子矩阵。接下来，在新的空间进行模糊度的搜寻，得益于新空间中模糊度参数之间的相关性显著下降，可以快速找到最优的模糊度组合。最终，将找到的精确模糊度组合通过逆转换回到原始空间。

模糊度搜寻和先前提到的降相关是LAMBDA 算法中两个互不相关的环节。即便不执行降相关步骤，我们依然能够执行模糊度的搜寻。整数模糊度的搜索要求（目标方程f）为：

在这里，N 代表已给出的浮点模糊度数组；QN代表浮点模糊度的方差- 协方差矩阵其逆则为浮点模糊度的权重矩阵表示整数模糊度数组。通过在搜寻空间中寻找一个使得该公式达到最小值，从而确定模糊度。

2 AR 策略

为实现更为高效与准确的模糊度固定，RTKLIB集成了多种策略，主要包括：instantaneous、continuous以及fix-and-hold 三种模式[6]。

瞬时解算(Instantaneous)：此策略中，每个历元都被视为一个全新的数据单元，不会受到其它历元中模糊度估计结果的任何影响。这种策略特别适用于那些不连续或断断续续的数据，因为每个历元的模糊度都是重新计算的，确保了其独立性和准确性。

连续解算(Continuous)：与瞬时解算相对，连续解算策略会将当前历元的模糊度浮点解作为后续历元的初始值，从而确保解算的连续性。此策略的优点在于，能够在多个历元之间共享模糊度的信息，从而增加解算的稳定性和可靠性。

固定并持续(Fix-and-hold)：此策略进一步提高了模糊度解算的动态性。在固定解被确定后，它立即被用于调整和优化当前的模糊度浮点解。这种“实时融合”的策略有助于快速反应并适应不断变化的测量环境和条件，从而提高整体解算的精确度。

总的来说，RTKLIB 提供的这三种策略均有其独特的优势，可以根据实际应用的需求和场景进行选择和调整。

3 强遮挡北斗监测站实验

为了探究不同模糊度确定策略对于在强遮挡条件下的北斗观测站的定位精度所产生的效果，本部分选择了某铁路连续梁的一个参考站与一个观测站进行科学实验分析。图1 描述的观测站环境表明，观测站所处的观测条件较为恶劣，其四周被铁制围栏所阻隔，这对模糊度的确定产生了负面影响。

图1 强遮挡北斗监测站

实验所用数据是在2022 年5 月3 日至10 日这一段时间内采集的，相应地，年积日（Day-of-Year，DOY）为该年度的第123 天直至第130 天。数据记录的时间间隔为1 秒，总的记录周期为7*24 小时，且所选的高度截止角为15°。基准站和监测站都配备了HG-GCYH8372 型的天线和CRDC01 型号的接收设备。

在此项研究中，采用了第2 小节所述的三种RTKLIB 定位计算策略，分别为：瞬时解算策略（Instantaneous）、连续解算策略（Continuous）及固定并持续策略（Fix-and-hold），旨在深入探讨北斗监测站的坐标数据系列。

图2 中左上区域呈现了不同策略的固定率数据，以便更细致地揭示各坐标分量的波动特征，纵坐标详细展示了NEU（北、东、上）各坐标分量。进而，右上区域显示了各策略的标准偏差与均方根误差，这二者均为关键的定位计算质量评估参数。标准偏差描述了数据的分散趋势，而均方根误差则阐述了预测与实际值的差距，为评定各计算策略性能提供了关键参考。此种多角度、多指标的评估方法有益于深度评析和对照三种策略处理北斗监测站数据的效果。

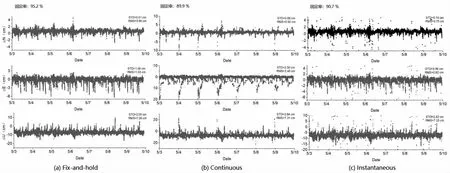
图2 三种策略解算的坐标序列

根据图2 的展示，三种解算策略：Fix-and-hold、Continuous 和Instantaneous 的固定率依次为95.2%、89.9%及90.7%。在此之中，Fix-and-hold 策略展现出了最高的固定率，随后是Instantaneous，而Continuous策略的固定率最低。然而，从定位精度的角度考虑，平面方向上，Instantaneous 策略的标准偏差小于0.8 cm，显示出最佳的定位精度。其次是Fix-and-hold 策略，其标准偏差小于1.0 cm，而Continuous 策略的定位精度最低，大约为2.3 cm。在高程方向上，这三种解算策略所展现的效果相似，大约在2～3 cm 之间。

再进一步观察均方根误差，可以明显地发现，这三种策略在U 方向都呈现出约7 cm 左右的系统性偏差。这种偏差是由于多路径效应导致的。值得注意的是，多路径效应不仅在模糊度解算上产生了不利影响，其影响还会在高程分量中呈现，体现为高程的系统偏差。因此，在进行进一步的分析和解算时，应该充分考虑并纠正这部分误差。

根据传统的监测技术，当解算出坐标序列后，为了提高数据的稳定性与准确性，这些序列首先会经历一个抗差处理过程，以消除或降低异常值的影响。接着，为了进一步优化数据质量，通常会采用滤波方法来减少噪声或其它随机干扰。在数据处理和优化后，为了方便后续分析，所得到的数据将会每隔1 小时进行一次平均，从而得到更为平稳的时序数据。最终，这些平均后的坐标值将与已知或真实的坐标进行比较，以评估解算坐标的准确性和可靠性。相关的图形展示与详细数据可以参考图3 及表1。

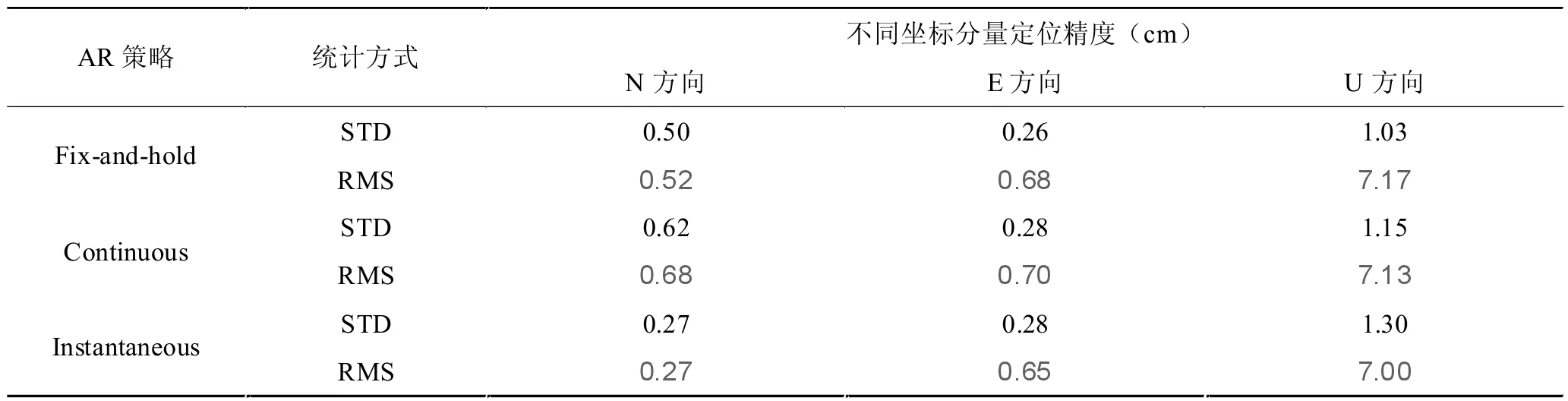
表1 滤波处理后监测结果统计

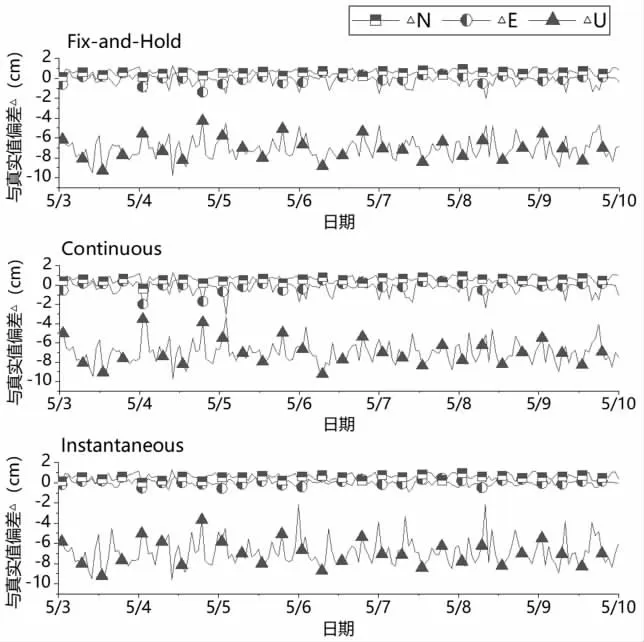
图3 滤波处理后监测结果

经详细数据分析，可以得出以下观察与结论：Instantaneous 策略在水平方向上展现出了卓越的定位精度，准确度达到了0.3 cm。相较之下，Fix-and-hold和Continuous 策略在同一方向的精度均为0.6 cm。对于高程方向的精度分析，Fix-and-hold 策略显示为1.03 cm，Continuous 策略为1.15 cm，而Instantaneous策略为1.30 cm。这指出，在高程方向上，三者均未达到理想的精确度。进一步地，经过抗差处理并排除了明显的粗差数据后，以及经过后续的滤波操作，依然可以观察到E 方向和U 方向受多路径效应影响的系统性偏差。更为具体地说，E 方向的系统偏差为0.7 cm，相对较小；而U 方向的偏差显著，达到7 cm，几乎是E 方向偏差的十倍。

综上所述，考虑多路径效应的显著影响，尤其是在U 方向的高程测量上，使用这些监测站进行沉降观测前，应当对多路径效应进行仔细的修正与校准，以确保测量结果的准确性和可靠性。

4 结论

本文基于RTKLIB 深入分析了北斗监测站在强遮挡环境下的三种模糊度解算策略：Fix-and-hold、Continuous 和 Instantaneous。 研 究 结 果 表 明，Fix-and-hold 策略在模糊度固定率上达到95.2%，领先于Instantaneous 的90.7%和Continuous 的89.9%。在水平精度上，经过滤波处理后，Instantaneous 策略以0.3 cm 的精度表现最佳。而高程精度中，三者差异不大，但在未修正多路径误差前，均不适于沉降观测。这些结论为北斗监测站在强遮挡环境中选择模糊度解算策略提供了有力依据，并为后续研究提供参考。