轨道交通车站项目施工多目标均衡优化研究

倪远红

(中铁二十二局集团第五工程有限公司，重庆)

我国轨道交通建设快速发展，通行里程不断增加。对于车站而言，受地质环境限制，施工过程复杂，风险性较高。工期、成本、质量和安全四大管控目标之间存在复杂的关联性，实现多目标管控的均衡优化，对于顺利完成车站工程的施工具有重要意义[1]。结合重庆某轨道交通车站项目，对工期、成本、质量和安全目标展开研究，提出基于粒子群算法的优化策略，并进行算例分析，验证优化方案的有效性。

1 项目概况

重庆某轨道交通车站为高架(部分地下)四层岛式车站，站台宽度为13.5 m。车站斜跨在四海大道上方，部分车站埋置于江南大道道路下方。车站主体轮廓尺寸总长165 m，宽22.8 m，主体建筑面积约9 000 m2。车站共设置3 个出入口和1 个换乘通道。该车站项目工期要求为18 个月，签约合同价格为8 700 万元。

2 轨道交通车站项目施工协调

2.1 地铁车站施工项目多目标协调

工程项目通常将进度、成本和质量目标作为协调重点。轨道交通车站施工项目中，还应考虑安全目标。施工过程中，一旦发生安全事故，对进度、成本和质量会产生严重影响。进度、成本、质量和安全之间相互影响，必须综合分析。

（1） 质量、成本、工期之间的关联性质量、成本、工期之间的关联性如图1 所示。

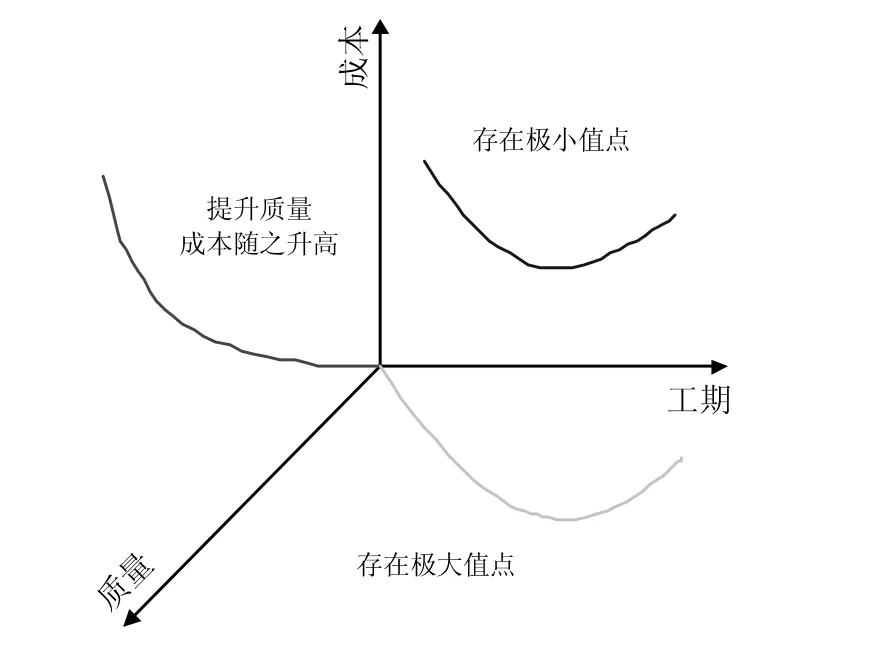
图1 质量、成本、工期之间的关联性

对于成本与工期而言，二者通常负相关，压缩工期意味着必须投入更多成本，但是存在一个最优化的成本和工期组合，表现为图1 中的极小值点。

在保持成本不变的情况下，工期与质量之间近似为二次函数的关系。随着工期的延长，施工质量会随之提高，但是存在一个极大值点，是质量和工期的最优组合[2]。超过临界点后，再延长工期，各工序的衔接关系会中断，施工质量反而会降低。

在既定施工进度计划后，施工质量与成本之间则为指数函数关系，追求高质量，必然需要增加人力、物力。如果对质量要求过高，成本会显著增加。

（2） 安全、工期、成本之间的关联性

安全、工期、成本之间的关联性如图2 所示。

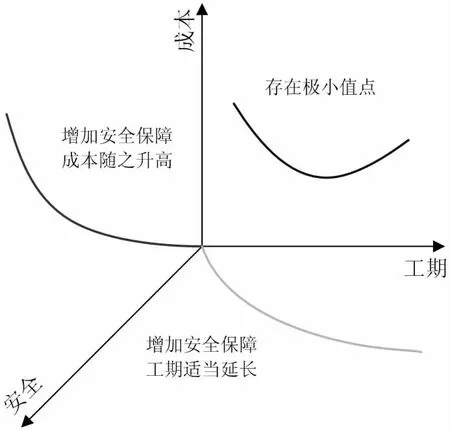
图2 安全、工期、成本之间的关联性

由轨道交通车站施工的复杂性决定的，成本与安全之间近似为指数函数关系。前期的安全性成本投入，对于保证安全性而言作用不显著，随着不断增加安全成本，安全性得到保障，趋向于某个稳定状态后，再增加安全投入，对保证施工安全的作用不明显[3]。

工期与安全的关系则近似对数函数，延长工期，各作业工序之间搭接较少，作业面单一，无交叉作业，施工安全得以保障。但是，无限制的延长工期，并不能带来安全性的持续提高，因为安全性趋于稳定后便很难提升。相反，若想压缩工期，则需要加大人力、物力投入。

（3） 地铁车站项目多目标关系分析

虽然很多情况下，成本与工期、质量和安全之间存在着对立关系，但在某些方面也存在着统一关系。成本与工期、质量和安全之间的对立统一关系如图3所示。

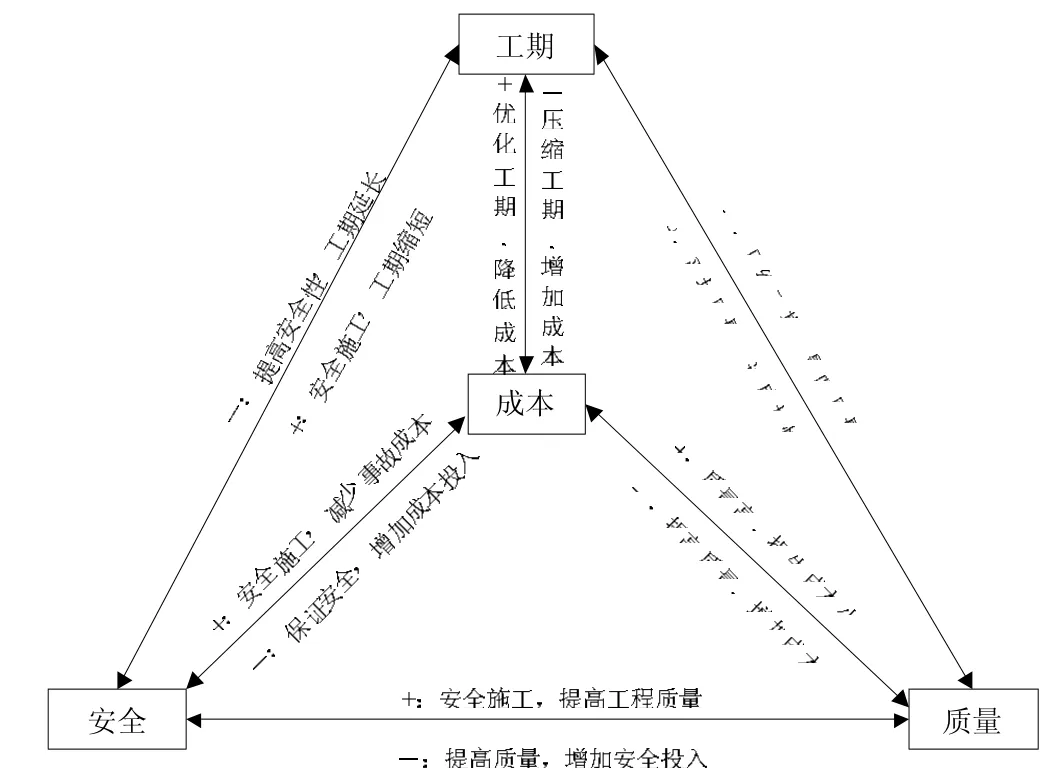
图3 成本与工期、质量和安全之间的对立统一关系

就对立关系，工期与成本、质量、安全的表现非常明显，而工期恰好是需要保证的基础条件，成本是优化的目标，质量和安全则是约束条件。

就统一关系而言，四大目标相辅相成，相互促进，共同决定工程项目的整体经济效益。在保证质量的前提下，可以减少质量问题、返工返修的损失成本，相应的工期损失也少[4]。在保证安全的前提下，无需应付安全隐患和安全事故，项目顺利完工，也减少事故损失支出和工期延误。所以，四大目标之间存在着一种均衡的最优组合。

2.2 地铁车站项目多目标模型

实际的地铁车站项目是一个复杂的工程，将其分解为18 个工序，用4 个参数描述。地铁车站项目的工序如表1 所示，质量指标和安全指标界定如表2所示。

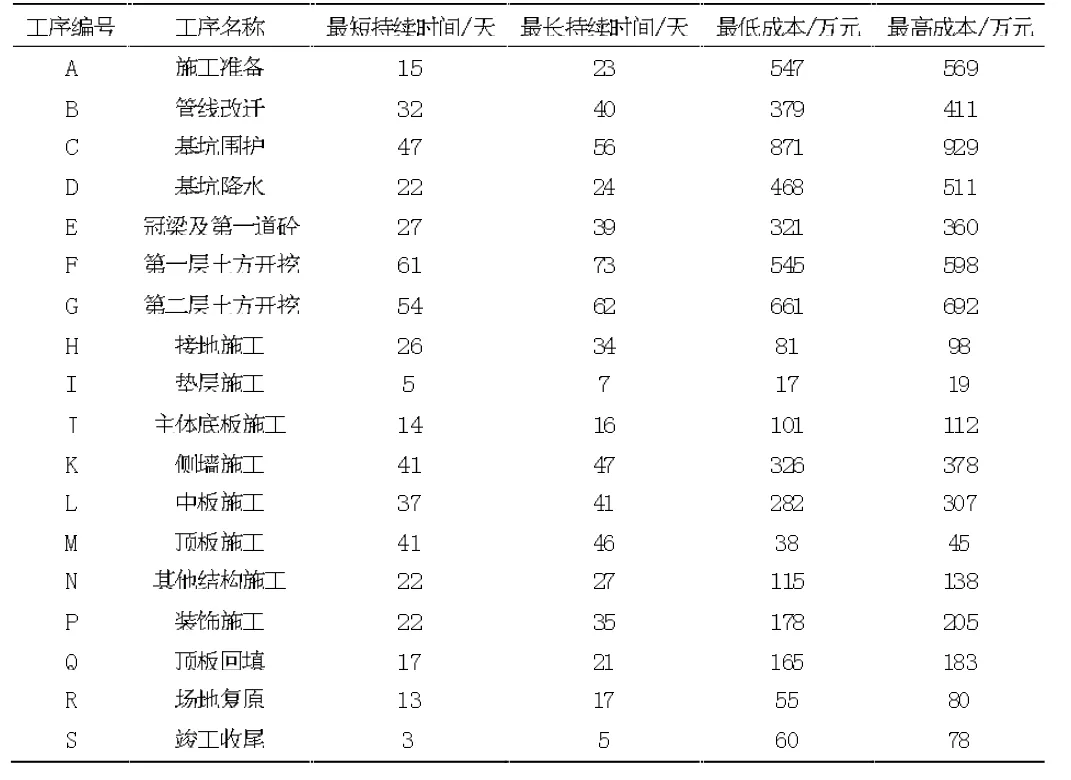
表1 地铁车站项目的工序

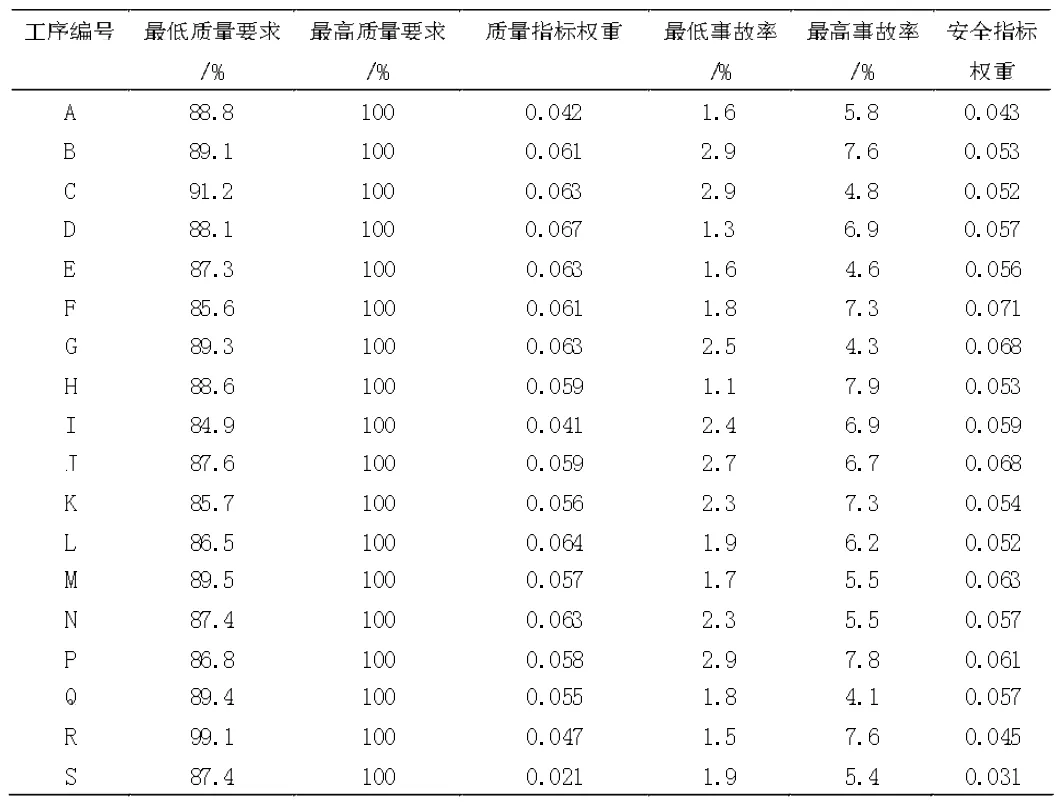
表2 地铁车站项目的质量指标和安全指标

（1） 工期-成本目标模型

轨道交通车站工程的工期-成本目标模型如下式所示：

（2） 工期-质量目标模型

轨道交通车站工程的工期-质量目标模型如下式所示：

（3） 工期-安全目标模型

轨道交通车站工程的工期-安全目标模型如下式所示：

3 地铁车站施工多目标均衡优化

工期与成本、质量、安全之间的均衡优化，是一个多变量的非线性问题，在建立目标模型的基础上，需要借助寻优算法求解。

3.1 目标函数建立

工期、成本、质量和安全的量纲不一致，无法直接组合成目标函数。基于多属性效用原则，将4 大目标的数据规范化为0～1 的标准值。由关键路线法可求得轨道交通车站项目的最长完成时间为290 天，最短完成时间为235 天。根据以往施工经验，估算该车站项目的最大直接成本为5 836 万元，最小直接成本为5 465 万元；最大间接成本4 276 万元，最小间接成本3 378 万元，提前完工的最大效益1 231 万元。因此，该地铁车站项目综合成本最大值为Cmax=10 112 万元，综合成本最小值为7 612 万元。根据表2 可知，该车站项目的最高质量要求为1，最低质量要求为0.856。最高事故率0.079，最低事故率0.011。

3.2 基于粒子群算法的多目标优化求解

为了对上述目标函数进行求解，引入粒子群算法。粒子群算法模拟鸟群或鱼群的迭代进化行为，在多变量空间中寻找最优解。借助Matlab 软件，按照表3 所示参数，进行求解计算。

表3 粒子群寻优求解计算参数

粒子群算法运行结束后，得到适应度曲线如图4所示，算法迭代至20 代左右即寻找到最优解，适应度值为0.998，表明多变量的求解精度很高。

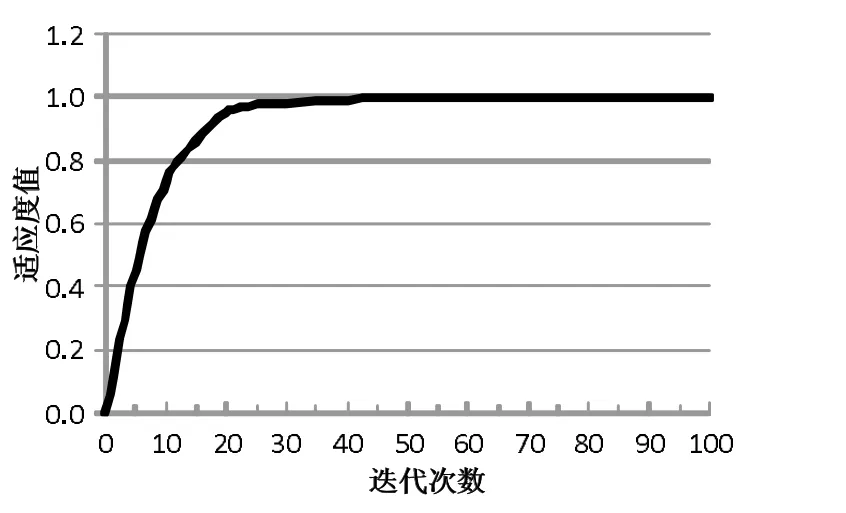
图4 适应度曲线

将最优结果解析之后，得到多目标均衡优化结果如表4 所示。

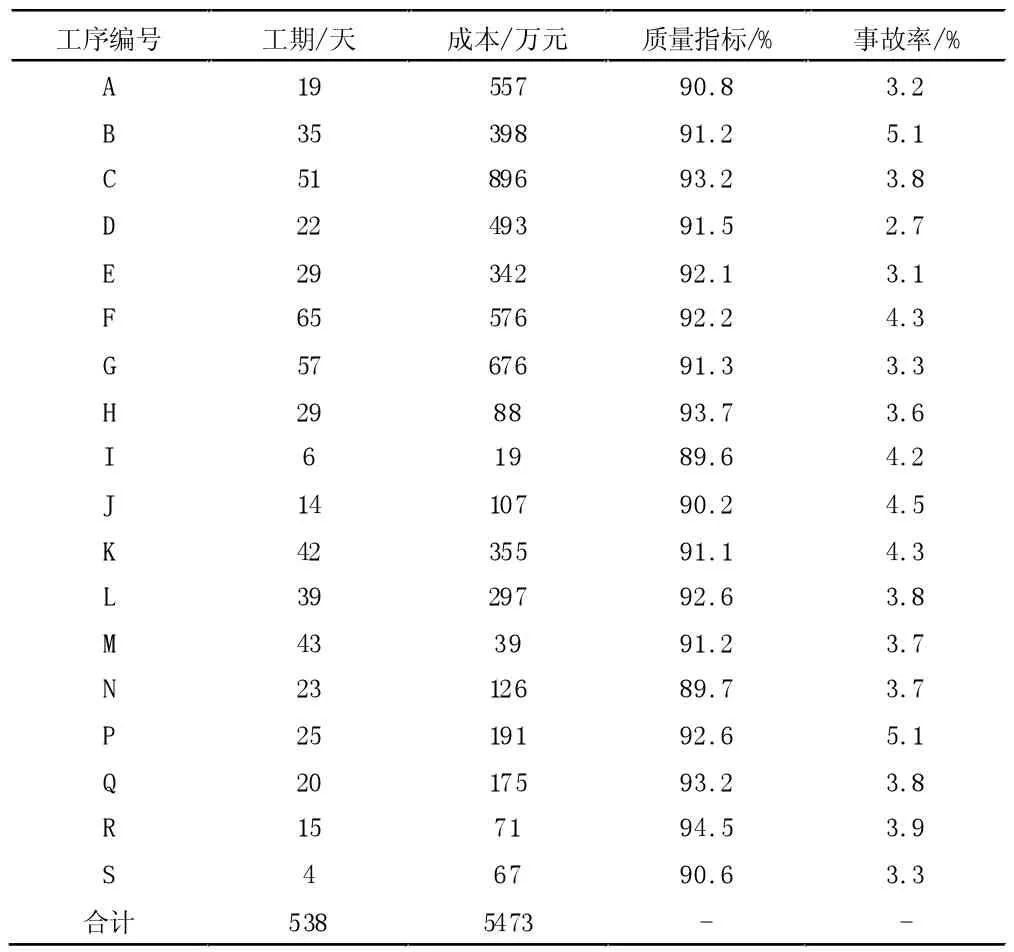
表4 地铁车站项目的质量指标和安全指标

经过均衡优化的各工序的持续时间，均处于最短持续时间和最长持续时间之间，总工期为538 天，小于合同工期18 个月(540 天)，工期符合要求。

经过均衡优化的各工序的成本，均处于最低成本和最高成本之间，总成本为5 473 万元，与签约合同价8 700 相比，毛利率为37.1%，可实现较高的经济收益。

质量指标和安全指标均在控制范围内，整体而言，该车站工程的多目标均衡优化方案切实有效。

结束语

结合重庆某轨道交通车站项目，对施工协调的多目标均衡优化展开研究，得出以下结论：

（1） 在分析工期、成本、质量和安全四个目标的关联性基础上，建立了多目标均衡优化模型。结合多属性效用原则，建立了多目标均衡优化的目标函数。

（2） 引入粒子群算法，对多变量问题进行寻优求解。算例数据表明，在保证质量指标和安全指标的前提下，经过均衡优化的总工期为538 天，符合工期要求；经过均衡优化的总成本为5 473 万元，实现毛利率为37.1%，利润可观。