Lightnin静态混合器内气液两相混合与传质强化特性

禹言芳，李毓，孟辉波，刘桓辰

（1 沈阳化工大学机械与动力工程学院，辽宁 沈阳 110142；2 中国石油大学（华东）新能源学院，山东 青岛 266580）

随着工业的迅速发展，能源被不断消耗，自然能源的开发利用受到了各国学者的广泛关注。而化工过程强化技术可以有效提高化学反应速率、多相混合效率、传热和传质性能，是节能降耗的一种重要手段[1-2]。静态混合器具有结构简单、维护成本低、低能耗等优点，被广泛应用于过程强化、食品加工、制药等领域[3-5]。与传统的鼓泡塔反应器相比，静态混合器有效增强管内的流体循环，从而强化气液两相流的混合效率及传质性能[6-7]。

目前，主要是通过实验研究及数值模拟方法研究静态混合器内气泡群的分散特性。Heyouni等[6]研究不同结构的静态混合器的压力特性及传质特性，总结了体积传质系数与表观液速和表观气速的经验关联式。结果表明：液相流速对压降的影响比气相流速更为显著。Azizi和Al Taweel[7]通过实验研究液相表观流速和气相体积分数对空气-水体系传质速率的影响，同时建立一个基于湍流耗散率、分散相体积分数和静态表面张力用于预测体积传质系数的经验关联式。Altabash 等[8]分别采用pH测量法、滴定法和直接CO2测量法研究筛网式静态混合器的强化吸收能力。结果表明：与鼓泡塔和机械搅拌罐等设备相比，筛网式静态混合器具有更为出色的强化传质性能。Rabha 等[9]利用色谱成像技术研究Kenics 静态混合器内的气泡尺寸分布（BSD）及流型转变规律。发现当液相表观流速小于0.2m/s 时，元件数量对气液相界面积和径向气含率分布几乎没有影响。螺旋静态混合器的量纲为1 Sauter 平均直径（d32）关联式不适用于预测垂直气液两相流动Kenics混合器的气泡尺寸。

Meinecke 等[10]使用背光成像技术（BST）和粒子图像测速（PIV）技术测量变形气泡表面积和气泡体积，同时研究了连续相流速、分散相流速和元件数量对CO2-甘油体系传质速率的影响。结果表明：连续相流速的增大能降低其停留时间从而降低传质效率，分散相流速的增大有效促进传质过程的进行。Scala等[11]利用BST技术和PIV技术研究SMX静态混合器的流动特性以及元件数量对气泡直径演变的影响。发现SMX 元件有效提高气泡的停留时间并促进气泡变形，同时15 个SMX 元件可实现气泡破碎与聚并的动态平衡。Meng 等[12]研究了三旋静态混合器中的气泡尺寸演变的规律，发现随着元件数量的增加气泡直径概率密度峰值变得更高更窄，且大气泡存在较为明显的拖尾现象。同时，获得了d32与量纲为1停留时间和液相韦伯数（We）之间的经验关联式。Xu等[13]研究了在Re为8000～160000、αd为3.23%～86.96%条件下水平放置的Kenics 静态混合器内的流型转变规律。同时调查了液相流量和气相流量对气泡群动力特性的影响，发现在气泡流中液相流量对BSD的影响比气相流量更为显著。

Zidouni等[14]使用双流体模型研究了Kenics静态混合器内局部气含率、液相流速和气相流速的轴向分布，结果表明：双流体模型可以有效预测气含率的径向分布。然而这项研究忽略了气泡的破碎和聚并，导致模拟结果与实验数据之间存在着巨大偏差。因此，建立一个用于准确描述气泡破碎和聚并现象的数学模型非常有必要。Luo 和Svendsen[15]指出，当湍流涡的能量大于发生破碎后的两个子气泡的表面能量之和时气泡就会发生破碎，同时基于湍流理论开发一个适用于气泡和液滴破碎的数学模型。Haddadi等[16]使用Luo破碎模型研究了Kenics静态混合器内的液滴行为，他们发现随着We和元件数量的增加，液滴尺寸逐渐减小，累积概率密度曲线向左移动。Meng 等[17]通过数值模拟的方法研究了Re处于8000～24000范围内Q型静态混合器内液滴的分散特性。研究发现，液滴在前两个元件处发生剧烈破碎，当元件数量大于10 时，液滴达到了动态平衡。Lehr等[18]发现气泡的破碎条件是湍流涡的惯性力大于较小子气泡的界面力。Wang 等[19]结合能量约束和应力约束建立一个新的气泡破碎模型，研究发现母气泡很难破碎成体积为无限小的子气泡。Wu等[20]利用CFD-PBM方法研究了旋流微气泡发生器内气泡的动力行为，通过数值方法证明Lehr-Liao模型可以准确描述旋流流场内气泡尺寸演化规律。

Han 等[21]研究了大于气泡尺寸的湍流涡对气泡破碎的影响，并通过数学建模的方法分析表面振荡对碰撞频率的影响；随后，提出了多重破碎的概念进一步阐述气泡破碎现象[22]；最后，研究了功率谱分布对气泡破碎速率的影响[23]。Zhang和Luo[24]研究了鼓泡塔内气泡发生破碎时所需的临界破碎能量，同时分析了黏性剪切以及气泡表面振荡对BSD 的影响。研究发现Luo-Luo模型严重高估了鼓泡塔内的气泡聚并速率，并错误预测径向气含率的分布。Xing等[25]研究了内部流动机制对气泡破碎频率的影响，并指出由于内部流动机制的存在，气泡更容易破碎为两个不同体积的子气泡。Liao等[26]结合了能量约束和应力约束开发了一套新的气泡破碎模型。发现当湍流应力大于由能量或气泡表面压力支配的临界应力的最大值时，气泡就会破碎。Huang 等[27]比较了Luo-Prince 模型、Liao-Liao 模型和Lehr-Prince模型对蛇形管式气液反应器内气泡尺寸预测的准确性。结果表明：Lehr-Prince 模型可以准确描述蛇形管式反应器内气泡尺寸的周期性变化规律。Guo 等[28]通过数学建模的方法证明当湍流涡的动能占据主导地位时，气泡倾向于破碎为两个体积相等的子气泡。而当应力能量足够大时，气泡趋向于非等尺寸破碎。Shi 等[29]研究了气泡形状变化对气泡破碎的影响，将气泡长径比引入气泡表面能增量中修正气泡破碎模型，并在鼓泡塔中验证了改进模型的有效性。Tsouris 和Tavlarides[30]基于湍流理论建立了一个半经验半理论的液滴破碎模型，然而该模型存在着多个经验常数，因此适用性受限。Azizi和Al Taweel[31-32]提出了一种求解离散群体平衡方程的新方法，并采用L-M 方法得到适用于筛网式静态混合器的Coulaloglou-Tavlarides 模型经验常数。Lebaz 等[33]重新评估基于湍流全能谱改进的破碎模型中的经验常数，并采取该模型合理预测了SMX+静态混合器的液滴乳化过程。

目前国内外学者对静态混合器的传热传质特性以及乳化特性进行了大量研究，然而对于静态混合器内气液两相分散混合特性仍不充分，这使得新型混合器的开发设计受到制约[16,34]。同时CFD-PBM模型预测模拟结果的准确性直接取决于破碎模型和聚并模型的选取[24,27]。为进一步丰富静态混合器的强化机制并拓展其工业应用领域，对Lightnin 静态混合器和Kenics静态混合器的传质特性和混合特性进行研究。因此，本文对Lightnin 静态混合器采用实验与数值模拟相结合的方法，在3.1～3.3 节中通过使用CFD-PBM 方法研究空气-水体系内气液相间界面积的演变规律，分析CoV 和拉伸率的轴向变化，定量评价LSM 和KSM 的分布混合及分散混合性能。此外，在3.4 节中基于实验数据研究液相表观流速和气相表观流速对LSM 内压差和流型转变的影响也是本文的重点研究对象之一，以期为后续新型混合器的设计及优化提供理论基础。

1 实验装置和方案

将12 个Lightnin 元件按照右旋-左旋的顺序依次交错90°排列形成LSM，几何模型如图1 所示。每个混合元件长度为100mm，长径比为1，元件厚度为2mm。在实验中使用的Lightnin 元件由聚乳酸材料（PLA）通过3D 打印技术（HORI-Z600，北京汇天威科技有限公司）制成。打印机的层高精度为0.05～0.8mm，XY轴的打印精度为0.01mm，Z轴的打印精度为0.05mm。混合元件放置于内径为100mm 的有机玻璃管中。Lightnin 静态混合器内气液两相混合实验装置如图2所示，空气和水分别由空气压缩机和不锈钢多级离心泵输送，其中空气和水的体积流量分别由精度等级1.5 的玻璃转子流量计和不锈钢转子流量计控制。玻璃转子流量计的测量范围为0.2～2.0m3/h，不锈钢转子流量计的测量范围为1～10m3/h。两相工作流体在喷射泵中初始预混合后由混合器的底部注入并在Lightnin 静态混合器充分混合。相机的测量坐标由3D 同步坐标架(234000 SDZ5835)控制，从上至下依次设置MW0652、MW0935、MW1150 和MW1227 共4 个轴向拍摄窗口，每个采集窗口的拍摄范围为344mm×200mm，各窗口位置测量范围分别为364～657mm、654～937mm、883～1168mm、953～1237mm。图像的采样时间为20s，拍摄帧率为180 帧/s。关于实验装置更多细节可以参考文献[35]。采用高速相机（Revealer-2F04M）拍摄和捕捉静态混合器内气液两相流场中气泡的形态特征。高速相机的精度为8bit，分辨率为1920×1080。使用Image-Pro Plus 6.0 准确获取气泡形态[12,36-37]。P1 处和P2 处的压力波动信号（PFS）时间序列由压阻传感器DY1400测量，精度等级为0.25，测量范围分别为0～40kPa及0～10kPa。压力信号由高频压力采集装置Dewetron-3021 采集，采样频率为1000Hz，每组工况测量3次以确保精度。

图1 LSM的模型结构

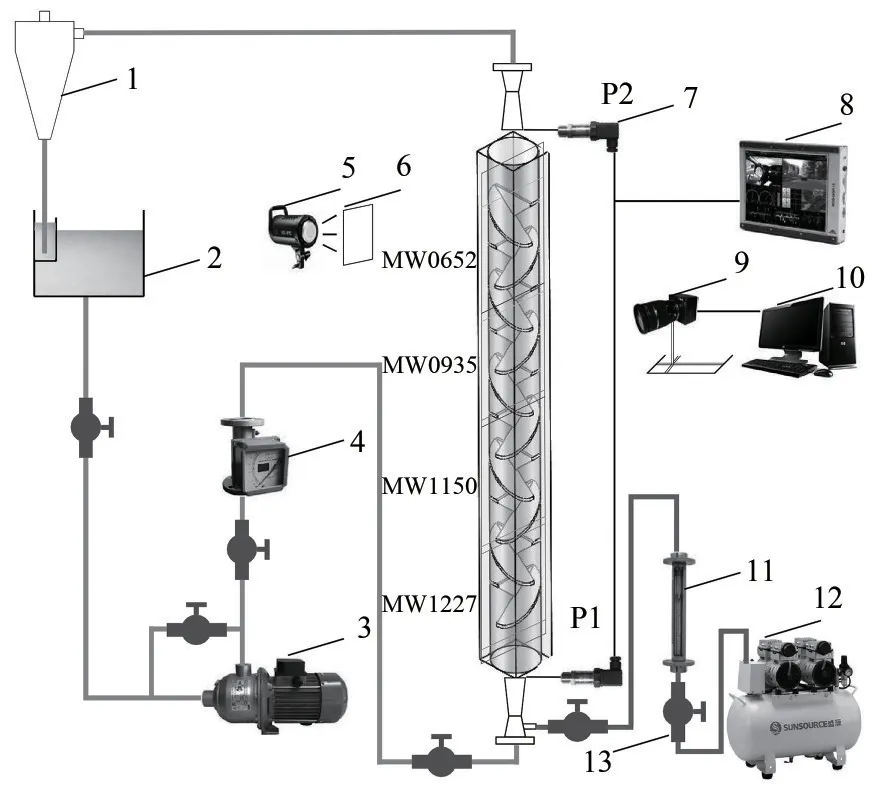
图2 LSM内气液两相流实验装置

2 数值模拟

2.1 控制方程

采用欧拉-欧拉模型模拟气液两相流动，水和空气同样被视作连续介质。式(1)和式(2)分别给出了质量守恒方程和动量守恒方程。其中F为相间作用力，CD为曳力系数。曳力是相间作用力中最为重要的力，曳力模型的选取直接决定模拟结果的准确程度。式(3)和式(4)分别给出了曳力和湍流耗散力的计算公式。Tomiyama模型[38]合理考虑了气泡形状对两相动量交换的影响，因此采用Tomiyama 模型计算曳力。湍流耗散力作为描述连续相湍流对分散相影响的径向作用力，同样对模拟结果有着相当大的影响。选取由Burn 提出的数学模型用于计算湍流耗散力。此外，由于旋流流场结构，升力和虚拟质量力的影响在本文中被忽略[20]。

式中，αi、ρi、Ui分别代表第i相的体积分数、密度（kg/m3）和速度矢量（m/s）；p为两相共享的压力，Pa；ζ为应力张量；FD、FT分别为曳力和湍流耗散力；db为气泡直径，mm。

2.2 湍流模型

湍流模型在模拟气液流动中起着重要作用。Meng等[39]使用不同的湍流模型计算了Lightnin 静态混合器中摩擦系数并与实验结果进行比较，发现SSTk-ω湍流模型具有最高的精度。Chen 等[40]证实SSTk-ω模型适用于预测旋流流动。因此选择SSTk-ω模型来预测LSM 以及KSM 中的流场。式(5)～式(8)分别给出了SSTk-ω湍流模型中k方程和ω方程的具体表达形式。

式中，σk,L和σω,L分别为k和ω的湍流普朗特数；Yk和Yω为k和ω由于湍流的耗散；Sk和Sω为用户自定义源项；μt为湍流黏度，Pa·s；F1和φ1为封闭系数；y为距离最近壁面的距离。

关于SSTk-ω模型的更多信息可以在Menter[41]的研究中找到。

2.3 气泡聚并破碎模型

群体平衡模型用于描述气泡的破碎以及聚并现象，它是气泡数量密度的输运方程。式(9)给出其具体的表达形式。

式中，n为气泡数量密度；V为气泡体积，mm3；S为气泡聚并和破碎的源项，由破碎核和聚并核共同决定。

Luo和Svendsen[15]假设气泡总是发生二元破裂，并且湍流是各向同性的。他们认为当湍流涡流的动能大于气泡的表面能增量时，气泡将发生破碎。破碎模型的具体表达式如式(10)所示，气泡和湍流涡的碰撞频率与气泡破碎概率的乘积被用于计算气泡的破碎速率。

式中，ε为湍流耗散率；λ为湍流涡尺寸；f为气泡破碎体积分数。

Lehr等[18]认为当湍流涡流的惯性力大于最小子气泡的界面力时，气泡会发生破碎。与Luo破碎模型的结构相似，Lehr破碎模型也给出了气泡和湍流涡流的碰撞频率和破碎概率的乘积形式。其破碎速率可通过式(11)获得。

式中，Wecrit为临界韦伯数。

气泡聚并模型可以由碰撞频率和聚并效率两部分组成。碰撞机制可归因于湍流涡脉动、浮升力驱动、尾涡夹带和黏流剪切，其中湍流涡脉动是决定气泡聚并最为重要的因素。Zhang和Luo[24]发现考虑黏流剪切的聚并模型总是高估了气泡的聚并速率，浮升力驱动和尾涡夹带对气泡聚并行为几乎没有影响。因此本文仅考虑湍流涡脉动对气泡聚并的贡献。此外，聚并效率决定了气泡发生碰撞后的聚并概率，同样对聚并速率有着重要的影响。根据排液速率模型理论，当相互碰撞的气泡间的接触时间大于聚并时间时，则两气泡发生聚并。Liao 聚并模型[26]、Prince 模型[42]和Luo 模型[43]均采用了这种假设，从而建立相应的聚并模型。Turbulent 聚并模型[44-45]给出与上述3 种聚并模型不同的表达式。Turbulent 聚并模型没有给出碰撞频率和聚并效率的表达式，采用Turbulent 聚并模型可以直接计算气泡的聚并速率。Turbulent 聚并模型将气泡的聚并机制分别归类于惯性子区的气泡聚并以及黏性子区的气泡聚并。Liao 和Lucas[46]对气泡聚并的建模工作进行了很好的综述。

2.4 边界条件

通过CFD 软件ANSYS Fluent 计算流场动力学参数。气体入口和液体入口被设置为速度边界条件。通过水力直径和湍流强度计算入口处的湍流条件。出口边界条件定义为自由流出，所有壁面均采用无滑移边界条件。与矩方法相比，采用均一离散法求解PBE 可以直接获得气泡尺寸分布，而矩方法需要将计算得到的矩值代入先验分布函数才可以获取气泡尺寸分布。因此，本文使用均一离散法求解群体平衡模型，其中class 数量直接决定PBE的求解精度。因此，本文调查了class 数量分别为9、16和20时对模拟结果的影响。在MW0935位置处，class 数量为9、16 和20 计算的气泡d32分别为3.272mm、3.192mm 和3.184mm。9 组class、16 组class 与20 组class 计算结果的相对偏差为2.76%和0.25%。因此，class 数量设置为16 用于后续求解。最大和最小气泡直径分别定义为12.50mm 和0.0004mm。采取Phase Coupled SIMPLE对压力速度耦合进行数值计算，动量方程采用一阶迎风格式离散，其他方程采用QUICK格式，连续性方程残差设置为10-4，其他所有方程的残差均设置为10-5。整体平均气含率由气相体积分数进行表示，其计算如式(12)所示[6]。

2.5 网格无关性以及模型有效性验证

与其他类型的网格相比，使用多面体网格可以提高计算效率并确保计算结果的准确性。多面体网格单元之间具有更多的接触面，因此，多面体网格可以得到更多的插值信息且具有更快的收敛速度。同时，与四面体网格和混合网格相比，使用多面体网格技术离散计算域可以有效降低总网格数量[47]。为保证数值计算的精确度，在混合元件与管壁接触的表面网格处进行加密处理。Meng等[39,48]采用多面体网格对整个计算域进行划分，并对壁面处网格进行加密处理，并保证壁面处的平均y+值均小于5。其数值模拟结果与实验结果具有很好的一致性。因此，本文采用多面体网格对LSM 的计算域进行离散化处理。在Re=14121 和αd为0.0697 的条件下进行网格无关性验证。第1 层网格高度为0.03mm，边界层为10 层。在Re=4000～21000 范围内壁面平均y+值为0.35～1.51。图3 显示了当网格数分别为1155575、1595714、1986823、2351793 和2779635时的压降和能量耗散率的计算结果。从图3可以看出，压降和能量耗散率随着网格数量的提高逐渐增加，最后趋于稳定。

此外，CFD-PBM 计算结果的准确性直接取决于湍流二阶量。能量耗散率直接影响LSM 中的气泡破碎率，并且可以通过测量的压降值来计算[7]。具体表达如式(13)所示。

与网格数为2779635时计算的能量耗散率相比，网格数为1155575、1595714、1986823、2351793时计算能量耗散率的相对偏差分别为5.31%、2.65%、1.13%和0.41%。因此，具有10 个边界层的2351793个网格用于后续计算。

为验证数值方法的有效性，在LSM 中进行数值模拟并与实验值进行对比。图4 展示了在MW0935 位置时通过CFD-PBM 方法（不同破碎核和聚并核的组合）计算和实验测量得到的d32数据，结果表明Luo-Turbulent 模型给出了对气泡d32最好的预测结果，而Prince 模型和Luo 聚并模型高估了气泡直径。Luo-Liao 模型和Lehr-Liao 模型低估了气泡尺寸。这主要是由于相较于Liao 聚并模型，Prince 聚并模型和Luo 聚并模型给出了更高的气泡聚并速率，Liao聚并模型低估了LSM内气泡的聚并速率[24]。因此，Luo 聚并模型总是给出最高的气泡尺寸，而Liao 聚并模型预测的气泡尺寸总是最小的。模拟结果与实验值之间的相对偏差见表1。

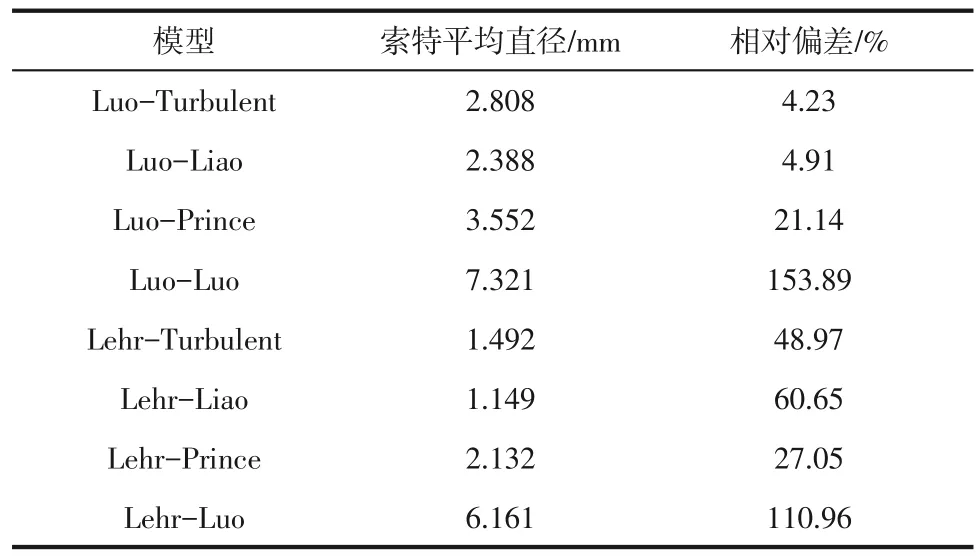
表1 不同模型计算结果与实验值对比误差

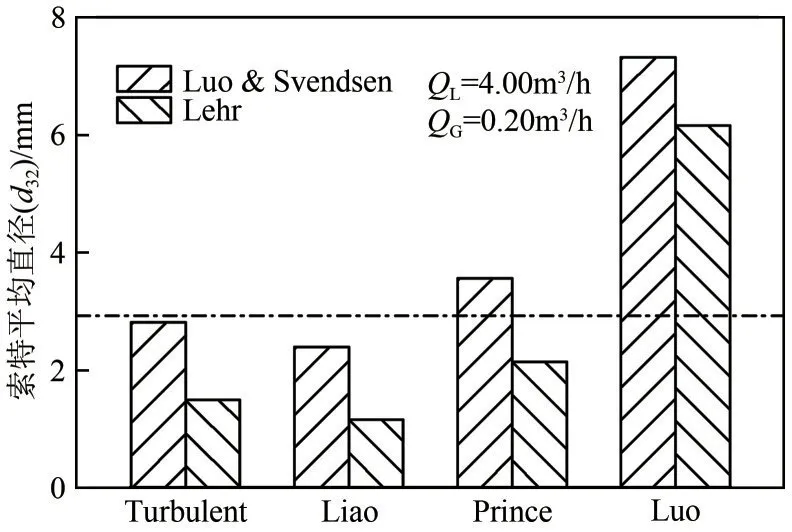
图4 不同聚并破碎模型预测的d32

此外，通过对比Luo破碎模型和Lehr破碎模型的计算结果不难发现，Lehr 模型预测的d32要小于Luo 破碎模型预测的d32。这可能是由于Luo 破碎模型预测的气泡破碎速率要小于Lehr 模型预测的气泡破碎速率。随着气泡直径的增加，Lehr模型预测的气泡破碎速率呈现出指数增长趋势，而Luo模型预测的气泡破碎速率呈现出线性增长趋势[20]。因此，Luo破碎模型计算的d32明显小于Lehr的预测结果。这也反映了选取合适的破碎模型和聚并模型对于预测LSM内气泡尺寸分布十分重要。

为了进一步评估Luo-Turbulent 模型对LSM 内气泡尺寸预测的准确性。图5(a)展示了当气相流量为0.30m3/h、液相流量为3.20～4.00m3/h 时MW0935位置处的气泡d32。随着液相流量的增大，气泡d32逐渐减小。这是因为增大液相流量，提高了LSM内小尺度涡的数量，提高了气泡与湍流涡的碰撞概率。模拟结果与实验数值的平均相对偏差为2.54%。图5(b)展示了当液相流量为4.00m3/h、气相流量为0.20～0.48m3/h时MW0935位置处的气泡d32。如图5(b)所示，随着气相流量增加气泡直径随之增加，气相流量的增加降低了小尺度涡的数量，同时提高了气泡间的碰撞频率。数值结果与实验结果之间的相对偏差范围为1.72%～3.83%，这进一步表明采用Luo-Turbulent模型预测分散相d32的数值是可靠的。

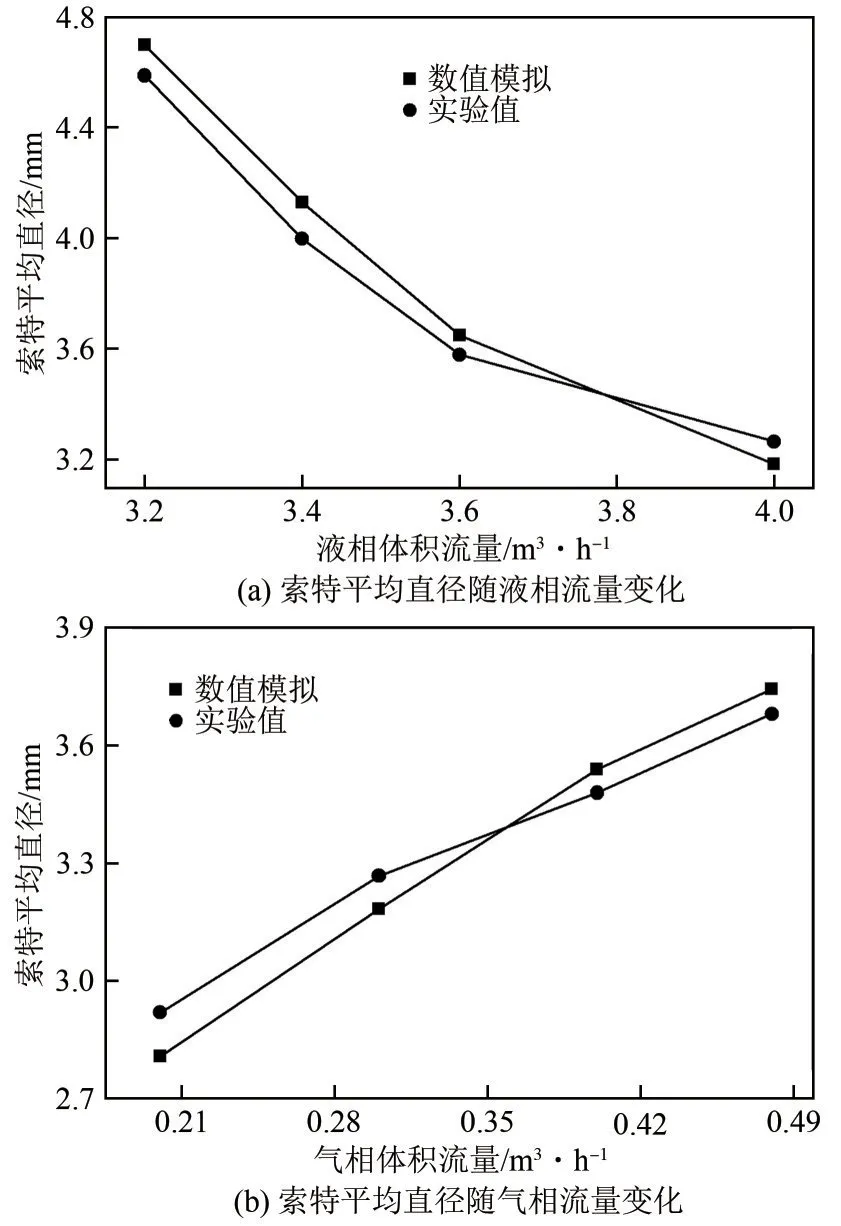
图5 数值模型有效性验证

3 结果与讨论

3.1 分散特性

气液相界面积（a，m-1）可作为一个重要参数用于表征两相传质速率，其表达如式(14)所示。

图6显示了不同Re数和αd条件下不同轴向位置的气液相界面积。如图6(a)所示，a随着Re数的增大而显著增加。当Re从4000增长至12000时，LSM的a增加1.93%～266.61%，KSM 的a增加2.27%～203.76%。相比于KSM，Re对LSM 内a的提升更为显著。此外，LSM 的a是KSM 的1.01～1.35 倍。这主要是由于LSM 破碎气泡的能力更强，这使得LSM 内的气泡尺寸明显小于KSM 的气泡尺寸。同时由于LSM 的压降显著大于KSM 的压降[39]，这使得LSM 内流体的Kolmogorov 尺度明显小于KSM。Luo 和Svendsen[15]发现，反应器内的Kolmogorov 尺度越小，其诱导的湍流涡数量密度就越大。因此与Kenics元件相比，Lightnin元件诱导更多小尺度涡，这进一步加强了气泡的破碎概率，致使LSM 具有比KSM 更为优异的分散性能。由图6(b)可知，a随着αd的增大而增大，当αd从0.03 增长至0.07时，LSM的a增加了1.02～1.45倍，KSM的a增加了0.99～1.45 倍。气相体积分数对LSM 和KSM 的分散特性影响几乎是等同的。这主要是因为与Re相比，αd对LSM和KSM的气泡尺寸影响更小。αd主要是通过影响局部气含率改变a。LSM 的a范围为15.82～85.89m-1，与KSM 相比增加了4.7%～25.9%。这也说明Lightnin 元件诱导的高剪切率流场促进了气泡的变形并进一步加强了气泡的破碎。值得注意的是，Re和αd对a的影响在更高元件数量的条件下更为显著。然而，当Re小于4000（UG/UL≥0.053）时元件数量对a几乎没有影响。这可能是由于过低的液相表观流速降低了混合器内的液体循环，混合元件对局部气含率以及气泡尺寸影响不大。

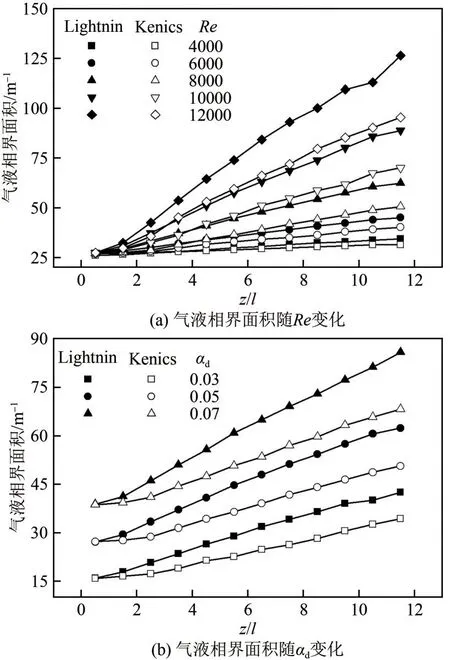
图6 不同条件下的气液相界面积变化

3.2 传质特性

采用湍流涡元胞模型计算混合器的体积传质系数[27]。图7(a)为LSM 和KSM 的kLa随轴向位置的变化曲线，气相体积分数为0.05。由图可知，随着元件数量的增加，LSM 和KSM 的体积传质系数分别增长了28.34%～360.69%和20.35%～247.52%。与气液相界面积的变化规律一致，Re对LSM 传质速率的提升更为重要。当Re等于6000、8000、10000和12000 时，LSM 的 体积传 质 系数为Re等于4000 时的1.37～1.81倍、1.75～3.14倍、2.10～5.30倍和2.43～8.72倍。随着元件数量的提升，Re对体积传质系数的强化效果更为显著。图7(b)展示了αd对LSM 和KSM体积传质系数的影响。当αd从0.03增长至0.07时，LSM的体积传质系数提高了1.06～1.51倍，KSM的体积传质系数提高了0.99～1.45倍。与KSM相比，αd的增加对LSM传质能力的增强更为显著，这主要是因为LSM 的a大于KSM。其次，Meng 等[39]发现，LSM的阻力系数基本是KSM阻力系数的1.8倍，LSM具有比KSM 更大的阻力系数，这表明LSM 的压降始终大于KSM的压降。根据式(13)可知，LSM的压降大于KSM 的压降即表明LSM 内流场的湍流耗散率大于KSM。一方面LSM 内过大的湍流耗散率增大了气泡的破碎速率，增加其气液相界面积；另一方面，湍流耗散率的增大促进湍流波动提高了液侧传质系数[27]。综上两点，LSM具有比KSM更为优异的传质性能。

图7 不同条件下的体积传质系数变化

3.3 混合特性

为了评估静态混合器的分布混合性能，使用变异系数（CoV）来测量LSM 和KSM 中的混合程度。CoV越小，混合效果越好，而CoV越大，混合效果越差，通常当CoV≤0.05可被视为完全混合。图8(a)显示了LSM 和KSM 内不同轴向位置处的CoV。如图8(a)所示，可以清楚地看到，CoV 值随着元件数量的增加而逐渐降低。对于LSM而言，CoV的减小主要可以分为两个阶段。首先CoV从第1个元件到第4 个元件急剧减小，CoV 降低了97.18%，4 个Lightnin 混合元件即可实现完全混合。当元件数量大于4时，CoV曲线基本保持稳定，可以忽略元件数量对分布混合的影响。对于KSM 来说，CoV 在前两个元件处均匀降低，其降低速率稳定保持在0.4。随后，在第3个元件到第9个元件处，CoV的衰减速率逐渐减小，最后两个元件处CoV值保持稳定。7 个Kenics 元件可保证混合程度大于95%。此外，当元件数量大于10 时，LSM 和KSM 的分布混合效率基本相同。图8(b)展示了LSM和KSM在轴向液相拉伸率（Λn）以及气相拉伸率。可以从图8(b)中清楚看出，LSM 和KSM 的液相Λn在1～8 个元件处均匀增加，LSM 的液相Λn是KSM 的1.06～1.16倍。这主要是由于与KSM 相比，LSM 对流体微元进行了更多的拉伸和折叠。而在第9～12 个元件处液相Λn的增长速率逐渐减小，液相Λn的增长速率稳定保持在0.37。这说明增加元件数量可以有效提升混合器的分散混合效率。图8(b)同时展示KSM和LSM 的气相拉伸率与元件数量的对应关系，KSM的气相拉伸率均随着元件数量的增加而均匀增长。LSM的气相拉伸率在前8个元件处逐渐稳定，在9～12 个元件处均匀增长。LSM 的气相Λn为KSM 的1.74～1.90 倍，这可以归功于LSM 诱导的小尺度纵向涡提高了气泡与混合元件的碰撞频率。

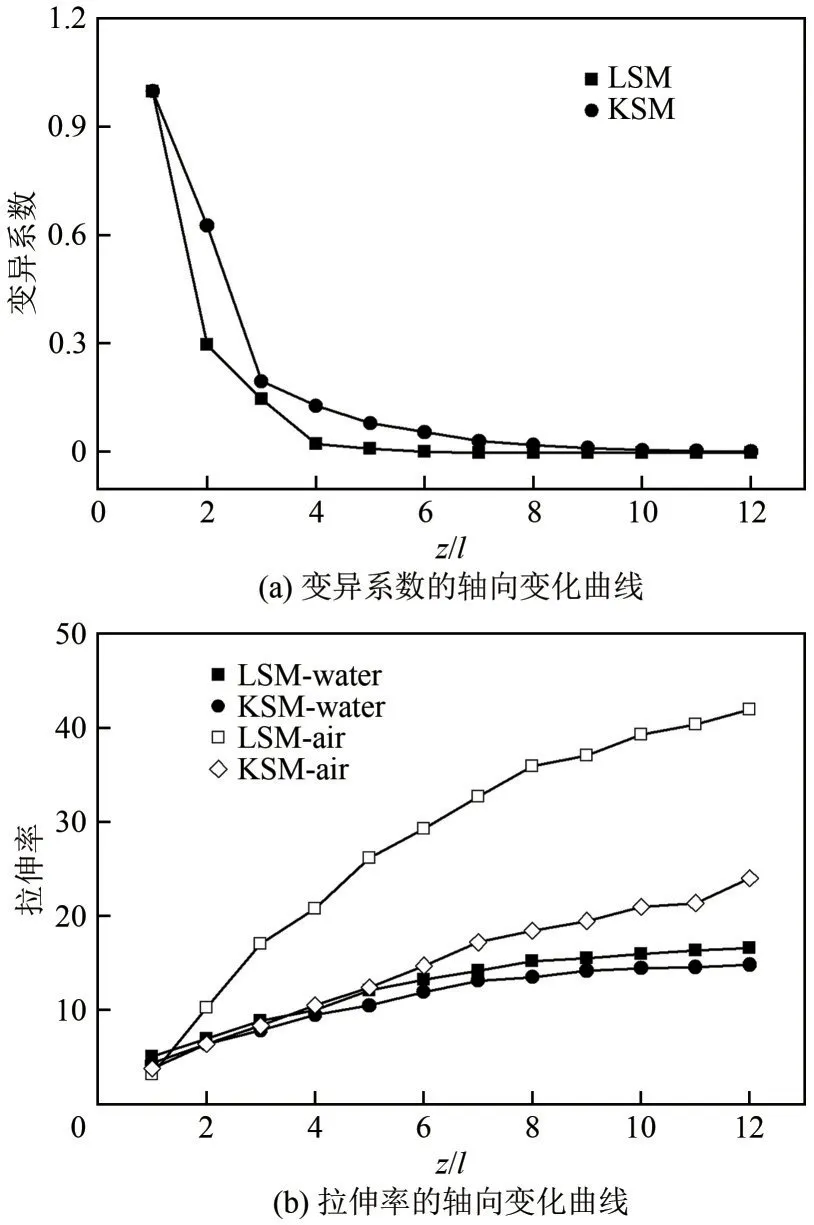
图8 Re=8000条件下CoV和气液两相拉伸率的轴向变化

由于G值可以通过模拟手段轻松获取，因此同时选取G值作为评价LSM和KSM混合效率的标准。对于静态混合器而言，G值可通过式(15)进行计算得出[49]。

图9展示了Re和元件数量与G值的关系。可以清晰看到Re的增大显著提高了G值，这表明Re的增大可以提高混合效率。当Re为4000～12000时，LSM 的G值是KSM 的1.37～1.61 倍、1.32～1.40倍、1.36～1.50 倍、1.37～1.51 倍和1.37～1.52 倍。这表明与KSM 相比，LSM 产生了更大的压降，这部分损失的能量迅速地将LSM 内的流体分散至Kolmogorov 尺度[4]。根据式(13)和Kolmogorov 尺度定义式不难发现，LSM内的Kolmogorov尺度明显小于KSM。Goldshmid 等[50]发现混合器内的最小尺度涡尺寸越小，其混合性能越好，这表明LSM 具有比KSM更为优异的混合效率。此外，还可以从图9观察到，G值同样随着元件数量的增加而提升。G值在前两个元件处急剧增加，在后续的元件位置处均匀增加，且G值的增长率随着Re的提高而进一步提升。同时，当Re小于6000时，处于第10个和第12个元件的G值保持稳定，这说明损失的这部分能量没有用于提高混合效率。图8也证明了当元件数量大于10 时，额外的混合元件仅仅增加了能量损耗，而对混合性能的提升微乎其微。

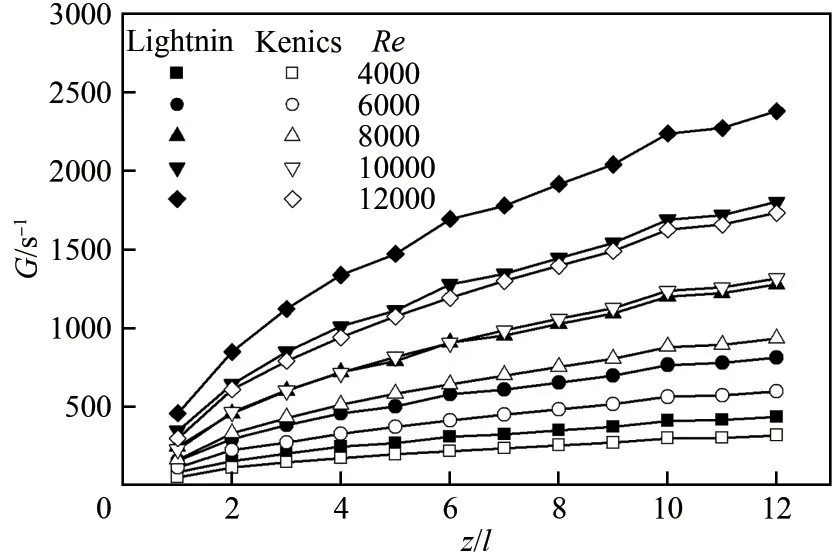
图9 不同雷诺数条件下G值与元件数量的关系

3.4 压力特性

由图9 可知LSM 具有比KSM 更大的压降，这部分能量用于强化气液两相传质以及混合效率。因此对LSM 压力特性的进一步理解有助于后续的元件结构优化。处于垂直管内的气液两相流动的压力损失主要由静压和与元件摩擦损失的阻力压降两部分组成[37]。图10展示了处于不同液相表观流速（UL）和气相表观流速（UG）条件下的LSM压降。当UL从0.092m/s 上升至0.127m/s 时，压降提高了1.77%～2.87%，UL的增大提高了水与混合元件的碰撞频率从而提高了能量损耗。气相流量的增大进一步提高了LSM 内气相体积分数，导致气液两相流静压随之减小。当UG从0.007m/s上升至0.042m/s时，压降降低了5.26%～6.29%。此外，当UL大于0.106m/s时压降出现了显著提升，这说明LSM 内的流型发生了明显的转变。UL的增大促进LSM 内的湍流脉动使气泡间的相互作用力增强，并且这种现象在较大的表观气速条件下更为明显。表观气速的增大强化管内的气泡诱导湍流，使气泡聚并及破碎更频繁，使流动状态从气泡流向湍动流转变，进而诱导气泡与元件表面发生碰撞，增大了管内二次流强度[37]。

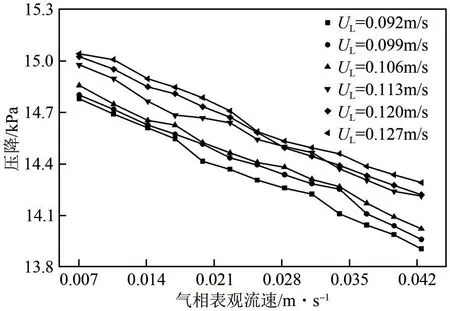
图10 不同UL和UG条件的压降曲线

如图11所示，LSM中P1和P2处压力信号的波动幅度随UG和UL而变化。压力标准偏差随着UL的增加而增大。如图11(a)所示。P1 的波动幅度随UG的增加而小幅度提高，当UG＜0.023m/s 时，其波动幅度小于0.093kPa。当UG＞0.023m/s 时，波动幅度随UL的增加而迅速增大。当UG=0.042m/s 时，其波动幅度超过0.104kPa。这主要是因为气相流速的增大使得入口处的气泡尺寸分布更为复杂，小气泡和发生剧烈变形的大气泡相互作用使压力波动更为频繁。显然，当UG＞0.023m/s 时，LSM 内的流型从过渡区转变为非均匀区，流型转变点出现在UG=0.023m/s。出口段的压力信号波动如图11(b)所示。由于入口处存在大气泡，P1 处的波动比P2 处的波动更剧烈。此外，P1和P2处的流型随UL的不同而明显发生变化，气相临界速度随着UL增大有延后的趋势。当UL＜0.106m/s 时，出口处流型转变的临界速度为0.023m/s。当UL≥0.106m/s 时，出口处流型转变的临界速度为0.029m/s。这主要是因为随着液相表观流速的增大，两相速度滑移比随之减小，气相对压力波动影响程度也随之减弱。

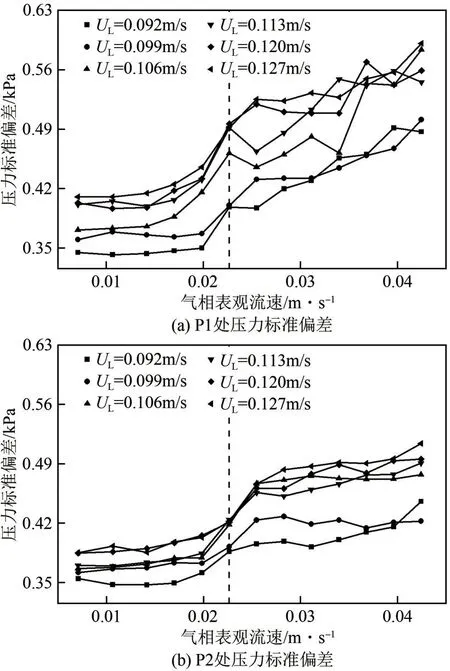
图11 不同液相表观流速和气相表观流速条件下入口和出口压力标准偏差

4 结论

采用实验与CFD-PBM 模型相结合的方法深入研究不同雷诺数、气相体积分数和元件数量对LSM和KSM 传质特性和混合特性的影响。通过对压力波动序列进行统计分析，以识别LSM 中的流型转变。得出如下结论。

（1）通过对LSM的实验结果与8种不同的聚并破碎模型的模拟结果对比，发现Luo-Turbulent 模型预测气泡尺寸更加贴合实验结果，所以采用Luo-Turbulent模型预测气液两相传质和混合是可靠的。

（2）体积传质系数和气液相界面积随Re和αd增加逐步增大，LSM 表现出比KSM 更为优异的分散性能和传质性能。元件数量对传质速率的提升幅度随着Re和αd的增加而更加显著。

（3）相比于Kenics静态混合器来说，LSM消耗了更多的能量用于提高混合效率。KSM需要7个混合元件可以实现混合程度大于95%。而3个LSM元件即可实现完全混合。LSM 的微观混合效率是KSM 微观混合效率的1.06～1.16 倍。LSM 的混合效率明显优于KSM。

（4）LSM 的压降随着UL的增大而提高，随UG的增大而降低，随着UL增大气相临界速度转折点存在延后的趋势。通过统计分析获得了气液流型转变的临界速度分别为UG=0.023m/s和UG=0.029m/s。