智能算法在地下供排水管网传感器优化布设中的应用综述
李清富 李泽祎
(郑州大学水利与交通学院,河南 郑州 450001)
0 引言
近年来,随着城市规模不断扩大,城市供水和排水管网的病害机理受到国内外越来越多学者的重视。城市快速发展导致老旧管网未能及时更替,导致管线事故频发。根据微信公众号“管线事故”发布的《2022 年度全国地下管线事故统计分析报告》显示,2022年1月至12月,发生在我国的地下管线相关事故就有1 418起。其中,管线破坏有1 162起,占比81.95%,路面塌陷事故244 起,占比为17.21%,其他类型的事故有12起,占比为0.84%。相较于2021年,2022 年度总体相关事故减少305 起,事故数量减少了17.70%。其中,地下管线事故减少193起,路面塌陷事故减少103起,其他类型事故减少9起。2022年度地下管线相关事故总体情况见表1。
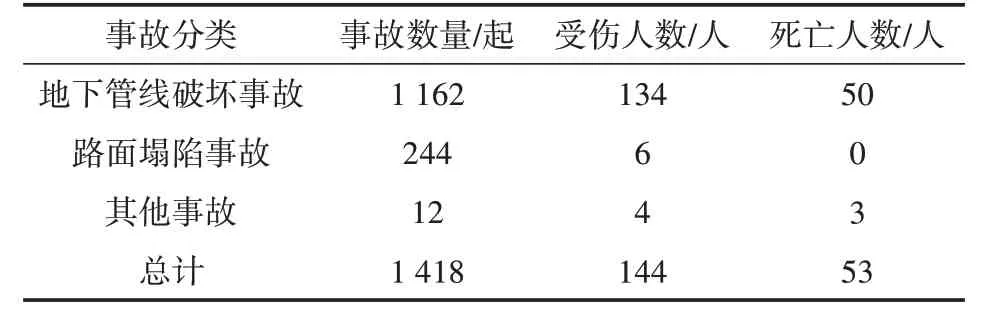
表1 2022年度地下管线相关事故总体情况
随着互联网技术发展,对城市供水和排水管道的监测已从人力监测向信号监测发展。因此,如何布设传感器及使用多少传感器才能获得更精确数据,成为亟待解决的问题。
1 传感器优化布置在构建一体化监测系统中的作用
在对城市地下供排水管网健康监测中,如何快速、及时获取准确信息,提高对结构监测的精度,是构建一体化监测系统不可避免的问题。在构建一体化监测系统过程中,传感器位置和数量的选择是关键一步,不仅影响系统经济成本,还对精确定位破损点有着不可或缺的作用。
1.1 传感器数量选择
从整个城市地下供排水管网服役里程来看,要实现对破损点的精确定位,需要非常多的传感器。在整个健康监测过程中,如果传感器数量过少,可能会造成信息缺乏或精度降低,健康监测结果可信度也会随之降低。如果传感器数量过多,会造成信息冗余,影响计算效率,导致计算结果精度下降,成本升高。因此,选择合适数量的传感器是构建一体化监测系统中的重要一步。
1.2 传感器位置选择
从全局来看,城市地下供排水管网空间分布广泛,无法在每个位置上都布设传感器。由于不同位置获取的信息量不同,且地下管网受土层压力和汽车荷载等的影响,在选择传感器位置时,要考虑管网、土层及其他因素产生的影响。传感器布设目标是在获取准确信息的同时,避免传感器在服役过程中被损坏。
2 智能算法在传感器优化布设中的应用
在传感器布设时,既要满足监测精度,又要保证传感器的数量在一定范围,从而保证经济合理性。对传感器位置的选择,本质上是在管网中找到最适合安装传感器的位置,而排列组合的运算量非常大。从80个可供选择的位置中选出30个来安装传感器,若采用排列组合法来求解,就需要1021次运算,而常用的计算机每秒平均运行次数为50 亿次,远远超出了计算机的运算范围。随着互联网技术发展,与工程实际相结合的智能算法也如雨后春笋般蓬勃发展。
在工程实践中通过怎样的“手段”来实现工程实践的目的是工程师们所关心的,而智能算法所要解决的问题就是找出全局最优的“手段”。目前,大部分智能算法以仿生学为基础进行研究。以粒子群算法(PSO)为例,PSO 起源于对鸟类取食行为的研究,而鸟类通过集体间的信息传播,使集体找到最优的目的地。将粒子群算法应用于传感器布设过程中,假设待优化问题的解为搜索空间中的一个粒子,那么粒子在求解空间中某个时刻的运动位置相当于布设传感器的位置,将在此位置所获取的信息与适应函数进行比较,从而保留最优位置,淘汰不利位置,然后通过不断迭代,得到全局最优解,即传感器最优的布设位置。除粒子群算法外,还有遗传算法、猴群算法、差分优化算法等。国内外对智能优化算法已进行了大量研究,为智能优化算法与工程实践的结合奠定了坚实的理论基础。
3 国内外研究现状
3.1 国内研究现状
随着国家基础设施建设的快速发展,国内越来越多学者开始研究工程结构中健康监测问题。在整个监测过程中,对传感器布设优化研究是至关重要的。
吴圣斌[1]提出改进的人工鱼群算法,用于优化传感器布设。由于聚群行为与追尾行为的本质相同,且聚群行为对算法的收敛性并非必需,因此,在改进的人工鱼群算法中,舍弃聚群行为。对算法追尾行为,通过增加高斯扰动项来提高算法精度。此外,运用Pareto 多目标优化的人工鱼群算法来解决传感器多目标优化问题,并以平面框架结构为算例,证明了使用改进的人工鱼群算法可获得较优的布设方案,安装在优化位置上的传感器可识别出损伤位置。
戴乐诚等[2]提出改进粒子群算法,用于优化桥梁结构损伤识别中的传感器布设。在改进的粒子群算法中,为解决因粒子“早熟”而引起的对局部搜索不透彻问题,引入惯性权重变量,改进更新方式,并在确定监测半径的条件下,寻找出传感器布设的最优方案。
高蕾[3]将适应度函数应用于遗传算法在拱桥监测传感器优化布置中。通过设置适应度函数,分别得到应用于拱桥主梁和拱肋的遗传算法,进一步提高传感器的布置质量和效率。
桂成中等[4]从振动模态角度出发,结合模态分量加合法(MSSP)和差分法(DM)对传感器布设进行优化,采用模态置信度准则检验法进行验证,并以铁路系杆拱桥的主梁和主振动模态为算例,对加合法、差分法和有效独立法的模拟结果进行分析,可知加合法和差分法的优化效果要优于有效独立法。
肖培源[5]以福州淮安大桥和福州三县洲大桥为例,对桥梁构件损伤识别中加速度传感器等的优化布置问题,提出基于改进遗传算法,从曲率模态识别的角度出发,通过分析曲率振型的不同影响因素,得到加速度传感器布设数量的下限,并利用修正的有效独立法,进一步确定传感器布设数目。研究结果表明,改进的遗传算法在目标函数求解上具有更高的稳定性和置信度,比传统遗传算法更优。
包龙生等[6]以连续梁桥为例,通过应用线性微分还原策略,降低粒子群惯性权重减小的速率,将典型线性递减粒子群算法改进为线性微分递减粒子群算法。研究结果表明,与传统粒子群算法相比,基于线性微分递减粒子群算法的传感器布设具有更强的适应性、稳定性及更高的使用价值。
朱航凯等[7]将遗传算法中的突变思想引入到PSO 中,利用自适应变异和线性动态权重对PSO 进行优化,并在两点走时计算中,利用最短走时的计算方式,实现2 m 以下误差的岩石破裂源定位。研究结果证明,改进的PSO 不会对传感器的排布方式及数量产生依赖,在实际工程中有较好的应用前景。
吕英迪[8]通过改进猴群算法和神经网络模型来对时域传感器布设进行优化。首先,以最小不适定性准则指标为算法目标函数,根据传感器布设累加规则,提出累加猴群算法,并对单一类型传感器进行最优布置。其次,提出一种基于双信号累加猴群算法,以平面梁模型为例,对多类型传感器布设方案寻优。最后,基于Pareto 理论进行多目标寻优,提出传感器布设的多目标综合寻优方案,并通过平面桁架模型和平面梁模型对传感器布设方案多目标寻优效果进行验证,结果表明,通过Pareto理论与累加猴群算法得到的传感器优化布设方案,能使各项布置指标更加均衡合理。
杨春霞等[9]以双塔斜拉桥为研究对象,采用有限元建模法,考虑到拉索锈蚀影响,并分析拉索破坏对周边拉索和主梁造成的影响,筛选出对破坏较为敏感的拉索,在破坏较敏感的位置布置传感器,实现以损伤敏感分析为判据的传感器优化布设。
农少校[10]在对传感器优化布设研究中,综合考虑参数识别误差、振动响应强度、模态独立性等因素对识别精度的影响,以帕累托方法为基础,建立三个因素两两之间的双目标优化准则,同时采用非支配排序遗传算法得到布设准则的帕累托前沿,通过平面二维桁架结构来验证所提出方法的可行性,并以润扬长江大桥的南汊桥主梁为例,对传感器进行多目标优化布设,进一步验证了帕累托多目标优化方法的可行性。
3.2 国外研究现状
目前,国外对传感器优化布设问题的研究集中在两个方面。一是传感器布设优化准则,即建立传感器各测量点的性能度量评估标准。二是选择优化算法,即在所有可供选取的结构集合中找出传感器最佳的布设位置。传感器优化布设理论最初是在数学和统计学基础上建立的,逐步发展到航空航天、工程结构等领域。
目前,常见的传感器优化准则主要有识别误差最小准则、模态置信度准则、模型缩减准则。①识别误差最小准则。该准则通过识别误差来构建性能函数,也被称为信息论优化准则。1983 年,Rafajlowicz[11]通过对Fisher 信息阵与输入谱密度和测点位置间的关系进行研究,提出在频域范围内传感器的最优配置。Kammer[12]在Rafajlowicz 研究结果的基础上,提出有效独立法(EFI 或EI)。此外,Kammer[13]还探讨过噪声对大型空间结构在轨道模态识别中传感器布设的影响,提出一种用于在轨道模态识别和测试分析相关性的传感器设置方法,是对有效独立法的扩展。该方法引入了噪声协方差强度矩阵,并将其看作成一个传感器的加权矩阵,从而改变目标模态形状。此外,还提出一种在传感器设置分析过程中使用的标准,以确定需要多少传感器来维持期望的信噪比水平,并通过简单的数值例子验证了该标准。②模态置信度准则。Carne等[14]在1994 年提出模态置信度准则,其是一种评价模态向量空间夹角的有效工具,以MAC 矩阵非对角元素值最小为寻优依据,使向量的空间夹角更大,模态向量彼此更加独立,从而获得更全面的模态信息。Cherng[15]采用信号子空间相关技术实现了对传感器的最优布置,并利用双层框架有限元模型进行了数值验证。③模型缩减准则。该准则基本原理是,当传感器被放在一个重要自由度上时,测量的准确性将得到改善。因此,该方法将模型的自由度分为主自由度和次自由度。在模型缩减时,主自由度保留了更多的模态动能,每次缩减后保留主自由度,删掉次自由度,将传感器布设在主自由度位置上,从而获得更加精确的数据。模型缩减法有Guyan 缩减法、改进缩减法、Kuhar 动力缩聚法、迭代的改进缩聚系统法、金丝循环缩聚法等。
随着智能算法的蓬勃发展,智能算法与工程结构健康监测相结合已成为目前研究热点。当前,被广泛应用的智能算法有遗传算法、粒子群算法、免疫算法、蚁群算法等。
遗传算法是基于达尔文生物进化论中的自然选择和遗传学机理生物进化过程的计算模型理论,通过对自然演化过程进行仿真,以寻求优化方案[16]。Cheriet 等[17]在对无线传感器网络中基于区域定位的最佳锚点位置时研究提出两种启发式算法,分别为本地搜索锚位置(Local Search Anchors Placement,LSAP)和遗传算法锚点布置(Genetic Algorithm Anchors Placement,GAAP),能解决由基于区域的定位算法来寻找最佳锚点的高复杂度问题。Tripath 等[18]为解决节点在无线网络中的最优部署问题,提出一种混合遗传规划(Genetic Programming,GP)和遗传算法(Genetic Algorithm,GA)的求解方法,该算法优化了网络的覆盖面积和节点部署数量,结果表明,该方法优于随机布局和一般的遗传算法布局。
粒子群算法(PSO)具有易于实现、计算精度高、收敛速度快等优点,是一种并行算法。粒子群算法是进化算法的一种,与模拟退火算法类似,PSO 也是从随机解出发,通过不断迭代来寻求最优解,并利用适应度函数来评价解的质量,与遗传算法相比,PSO 更简单,不需要遗传算法中的“交叉”和“变异”运算,而是通过追随当前搜索到的最优解来寻找全局最优。Ngatchou 等[19]提出一种适用于高维优化问题的顺序粒子群优化算法(Sequential Particle Swarm Optimization,S-PSO),不同于标准的PSO,S-PSO 是在参数搜索空间的随机子空间中进行迭代优化的,其在解决低维子问题时所需的粒子更少。仿真结果表明,S-PSO 在收敛性方面和计算效率方面都优于标准的粒子群算法。
免疫算法是把免疫理论应用于遗传算法中,在保留遗传算法优良特性的同时,有选择、有目的地利用代求问题中的某些特征信息和知识,来抑制优化过程中的退化现象。免疫算法与生物免疫系统机制相似,构造具有动态性和自适应性的信息防御体系,保留有利信息,抵御有害信息。蚁群算法是通过对蚁群搜索行为进行分析,从而提出的一种群集智能算法。一方面,利用蚂蚁觅食行为的正反馈机制来保证蚁群算法寻优的快速性。另一方面,利用蚂蚁觅食行为的分布式特性来避免算法的早熟性。同时,利用蚁群系统的贪婪启发式搜索特征,使其在优化初期就能获得较好的结果。
4 结语
目前,国内外有许多学者对传感器优化布设准则及优化智能算法进行了大量研究,为后来者在传感器优化布设方面提供了丰富的理论基础和试验算例,但目前对传感器优化布设的方法在工程实际和算法中的应用还存在一些亟待解决的问题。
首先,无论是传感器的优化布设准则,还是智能优化算法,二者与工程应用的结合多数是用于桥梁等地上结构的健康监测中,在管道结构健康监测中的应用较少。城市地下供水管道多数敷设在地下,受车辆荷载、降雨、温度及管道间相互作用等的影响,对传感器敷设要求也会随之提高。因此,如何通过优化传感器布设来提高对地下结构健康监测效率是目前城市地下管网监测中亟待解决的问题。
其次,大多数关于传感器优化布设的研究是在传感器数量已知的前提下进行的,而传感器数量的多少会影响最后的数据精度。同时,不同于地上结构,地下结构一旦敷设完成,后期修补会产生较大的经济成本。因此,如何确定传感器数量,并兼顾监测精度与经济成本,也是目前急需解决的一个问题。
最后,对传感器的优化布设多数是基于单一目标进行的。在实际工程应用中,待测结构大多数是处于复杂环境中,且各个目标会存在冲突,若对一种目标过分追求优化,将会不可避免地降低传感器对其他目标的监测精度。因此,需要找到更合理的多目标优化布设方法来解决复杂工程中传感器布设问题。
综上所述,城市地下供水排水管网健康监测已成为亟待解决的问题,同时也需要找到一种优化布设方法来同时满足传感器布设数量及多目标优化要求。因此,基于PSO 及Pareto 多目标优化理论对城市地下供水排水管道传感器进行优化布设,同时考虑管网运行状态指标、管道结构监测指标和环境监测指标来进行多目标寻优将成为未来研究趋势。

