稳态非线性热传导问题的比例边界有限元法

李庆华，冯子超，陈莘莘，孔祥禄

（1.华东交通大学土木建筑学院，江西 南昌330013； 2.中国铁路哈尔滨局集团有限公司，黑龙江 哈尔滨150001）

材料参数随温度变化引起的非线性热传导问题广泛存在于航空航天、生物医学工程和冶金工程等诸多实际工程领域[1-3]。 由于非线性热传导问题的复杂性，很难得到解析解，因而研究其数值解十分必要。 Thakur 等[4]求解了二维非线性瞬态热传导问题。 王峰等[5]采用基于Kriging 插值的MLPG 法分析了二维非线性稳态和瞬态热传导问题。 Yang 等[6]采用径向积分边界元法分析导热系数随温度变化的瞬态非线性热传导问题。Cui 等[7]采用单元微分法分析多维瞬态非线性热传导问题。 朱强华等[8]提出了一种基于特征正交分解（POD）和有限元法的瞬态非线性热传导问题的模型降阶快速分析方法。Mierzwiczak 等[9]采用Kirchhoff 变换对导热系数随温度变化的稳态非线性热传导问题进行线性化，并采用奇异边界法进行分析。

作为一种半解析的数值方法，比例边界有限元法[10]只需对计算域的环向边界离散为单元，并且在未离散的径向可以解析求解。 相对于边界元法，这种方法不需要基本解，也不涉及奇异积分的数值困难。 目前，比例边界有限元法已被用于求解断裂力学问题[11-12]、弹性动力学问题[13-14]、波导本征问题[15]、土-结构动力相互作用分析[16]和热传导问题[17]。 但目前尚未见到采用比例边界有限元法进行非线性热传导问题的工作。

鉴于比例边界有限元法的显著优势，本文将其与Kirchhoff 变换[18-19]相结合，提出了求解稳态非线性热传导问题的一种新方法。 利用Kirchhoff 变换，将非线性的偏微分控制方程转化为线性方程，然后采用比例边界有限元法求解，并借助Kirchhoff 反变换求得温度场。 最后，通过两个典型算例验证了本文所提方法的有效性。

1 稳态非线性热传导问题

考虑一个二维稳态热传导问题， 其计算域为Ω， 边界为Γ。 当热传导问题的导热系数随温度变化，且无内热源，则相应的控制方程和边界条件可写为

式中：k（T）为随温度变化的热传导系数；T 为温度；n 为边界外法向向量；Γ1为Dirichlet 边界；T¯为其上给定的温度；Γ2为Neumann 边界；q 为其上给定的热流密度。

为了消除式（1）的非线性，本文采用Kirchhoff变换[18－19]。 引入下式定义与温度相关的新变量

2 比例边界有限元法

考虑如图1 所示的比例边界坐标系，相似中心为点O，要求从该点可以看到边界上任意一点。 对于有限域问题，径向坐标ξ 的变化范围从0 到1，即0≤ξ≤1。 当相似中心点与直角坐标系原点一致时，计算域内任意点的笛卡尔坐标（x^，y^）可写为

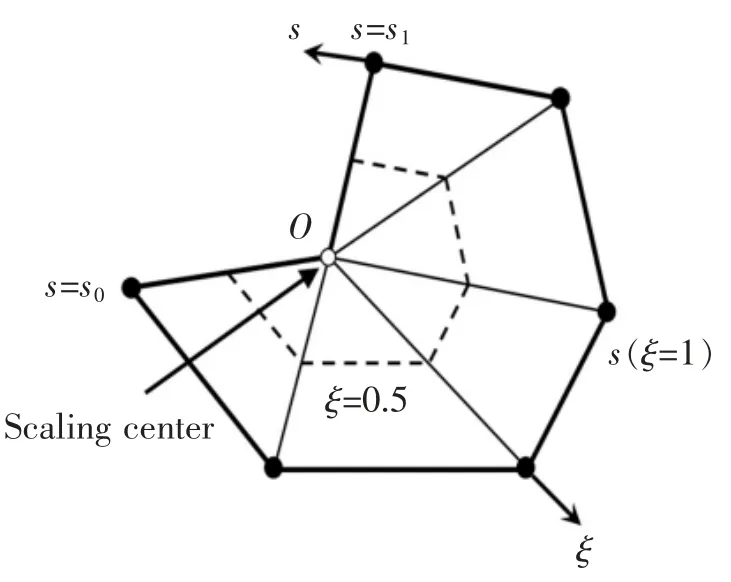
图1 比例边界坐标系统Fig.1 The scaled boundary coordinate system

式中：（x（s），y（s））分别为边界上任意点的笛卡尔坐标。

在比例边界坐标系下，梯度算子可表示为[14－15]

式中：N（s）为边界结点形函数。

将式（12）和式（15）代入式（14），然后对含δθ（ξ），ξ项做分部积分，并考虑δθ（ξ）T任意性整理可得

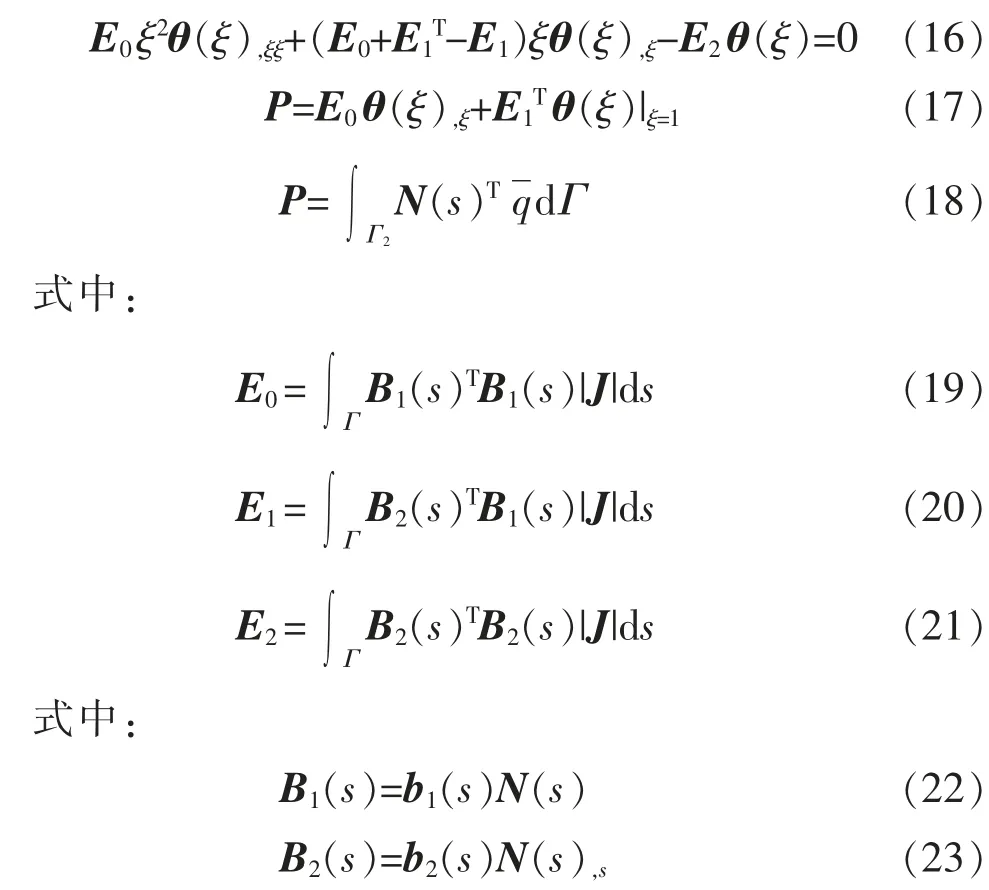
式（16）为二阶常微分方程组，采用矩阵函数[20]法可将其解表示为

式中：Sn为与负特征值对应的Schur 标准型；Ψθ为Schur 分解中与θ 变量相关的模态；c 为可由边界条件确定的积分常数。

将式（24）代入式（15）可求得域内各点的变量θ（ξ，s）值后，由Kirchhoff 反变换式（6）可进一步求得相应各点的温度T（ξ，s）。

3 数值算例

为了验证所提方法的有效性，本文对一些典型的稳态非线性热传导问题进行分析求解，并与相应的解析解进行了对比。

3.1 算例1

考虑一个边长为1 的方板的稳态非线性热传导问题，如图2 所示。 板的上端和下端为绝热边界，板左端的温度保持为Tl=300 K，右端的温度保持为Tr=400 K。

图2 算例1 和算例2 的模型Fig.2 The model of example 1 and example 2

导热系数与温度的关系为

计算时取k1=-2 和k2=0.01，将相似中心取在方板中心，并将边界离散成16 个二次单元。 采用本文方法，可以计算得到m 取不同值时y=0.5 处的温度分布，如图3 所示。 为了方便比较，图3 还给出了相应的解析解。 由图3 可知，本文方法计算精度很高，与解析解之间的最大相对误差只有2.02×10-10%。

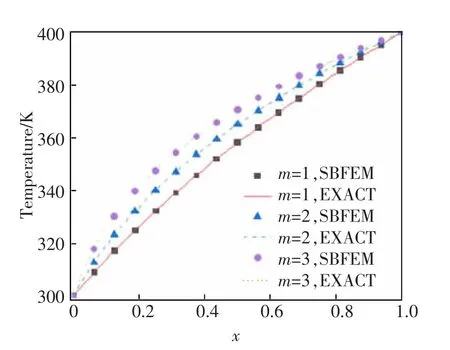
图3 算例1 中y=0.5 处的温度分布Fig.3 Temperature distributions at y=0.5 for example 1

3.2 算例2

算例2 同算例1 一样，只是导热系数与温度的关系假设为

计算时取k1＝-2，将相似中心取在方板中心，并将边界离散成16 个二次单元。 图4 给出了k2取不同值时y=0.5 处温度分布的数值解和解析解的比较。 显然，本文数值解与解析解吻合非常好（最大相对误差为2.32×10-10%）， 这进一步验证了本文所提方法的有效性。

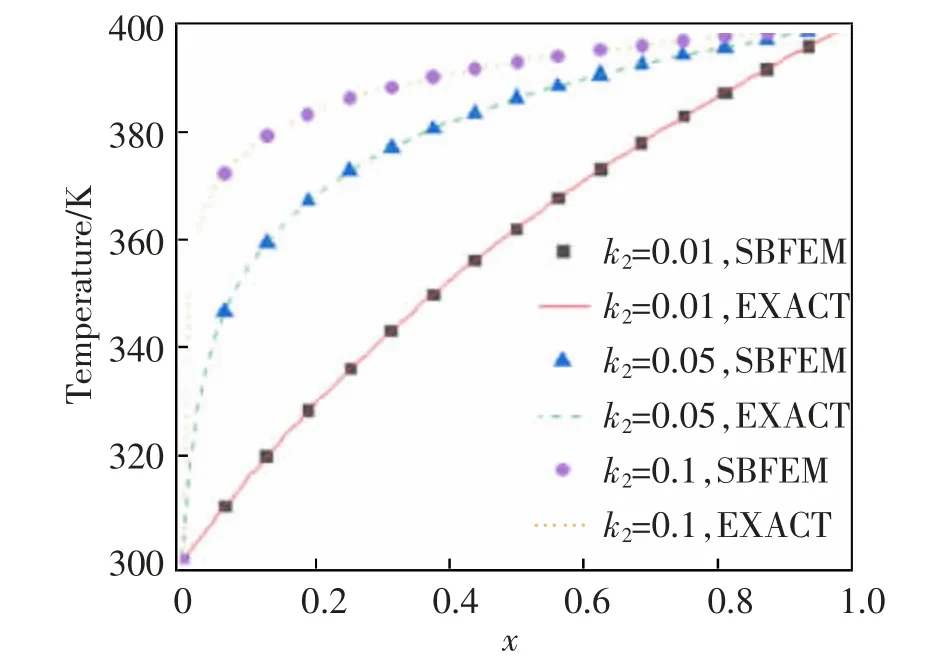
图4 算例2 中y=0.5 处的温度分布Fig.4 Temperature distributions at y=0.5 for example 2

4 结论

本文首次采用比例边界有限元法，建立了稳态非线性热传导问题分析的整套求解算法。 由本文分析和算例求解结果可以看出。

1） 不同于迭代解法，对于导热系数随温度变化的稳态非线性热传导问题应用Kirchhoff 变换可转化为线性热传导问题进行求解，进而可以避免迭代计算。

2） 作为一种半解析的数值方法，比例边界有限元法具有精度高、 计算量小和数学处理方便等优点，在拉普拉斯边值问题的求解中同有限元和边界元相比更具优势。

3） 数值算例验证了本文方法在求解稳态非线性热传导问题时具有较高的计算精度和计算效率。