基于氧气A 带吸收线的被动式对流层风场探测关键参数分析

刘欢，冯玉涛，傅頔，赵珩翔，孔亮，郝雄波，畅晨光，韩斌，王素凤

（1 中国科学院西安光学精密机械研究所 光谱成像技术重点实验室，西安 710119）

（2 中国科学院大学，北京 100049）

0 引言

风场信息是表征大气动力学的重要参数，也是影响大气物质、能量分布以及时空变化的重要因素。实时高精度的风场数据在提高天气预报精度、保障航天器起降安全、大气污染物追踪、无线电声波探测等方面发挥着重要作用［1-3］。对流层与人类的生产生活密切相关，但其大气环境复杂多变，使得风场探测较为困难［4］。

大气风场探测包括原位探测和遥感探测两种方式，其中遥感探测又分为主动遥感和被动遥感两种。探空气球和风速计是常用的原位探测仪器，可以快速获得风场信息，但无法实现大空间尺度的连续观测。雷达、激光雷达、微波雷达等是常用的主动遥感探测仪器，拥有时空分辨率和探测精度高的优点，但在仪器设计上较为复杂，费用较高。被动遥感只需设计一套接收系统，结构简单，成本较低，可实现全球或区域大范围连续观测，且探测精度较高，应用前景十分广阔［5-6］。

氧气作为地球大气层中的主要成分之一，含量稳定，在可见光、近红外和微波波段均有特征吸收谱，在可见光和近红外波段，有三个因氧气分子吸收而形成的吸收带，分别是氧气γ 带，氧气B 带和氧气A 带，A 带的吸收强度比γ 带和B 带都大，且无其他气体干扰，是理想的对流层风速大气探测源，而γ 带和B 带主要用于平流层风场探测［7-9］。1991 年，搭载于高层大气研究卫星上（Upper Atmosphere Research Satellite，UARS）的高分辨率多普勒成像仪（The High-Resolution Doppler Imager，HRDI）利用氧气B 带和γ 带吸收线的多普勒频移实现了对流层上层和平流层的风场探测，其光学结构采用三个依次排列的法布里-珀罗（Fabry-Pérot)标准具，对加工精度要求很高［10-11］。2004 年，美国宇航局通过了一项被动氧气A 带测风仪（Passive ABand Wind Sounder，PAWS）计划，PAWS 使用等厚干涉的Michelson 干涉仪，采用临边观测模式观察大气风场，利用氧气A 带吸收线的多普勒频移测量0～20 km 大气高度的对流层风速，将来自大气柱每1 km 的大气信息同时成像在探测器上。在对流层风场探测中，干涉仪和滤光片的参数对风速测量有较大影响，因此合理设置相关参数对于提高探测精度十分重要［12-13］。

本文基于氧气A 带吸收线测风原理，探索利用多普勒差分干涉仪（Doppler Asymmetric Spatial Heterodyne，DASH）实现对流层风场探测的可行性，参考仪器工程设计理论建立了星载临边观测正演理论模型并进行风速反演理论模拟，分析了干涉仪非对称量、光谱分辨率、带通滤光片带宽、Fabry-Pérot 标准具两板间距及精细度系数变化、干涉图噪声、仪器稳定性和标准具离轴效应对风速测量精度的影响。

1 风场探测原理

多普勒差分干涉仪通过探测氧气A 带吸收线的多普勒频移反演对流层风速。根据多普勒效应，所探测的光谱吸收线随大气风速产生频移，频移之后的谱线中心波数σv为

式中，σ0表示无频移的谱线中心波数，v表示仪器视线方向风速，c表示光速。对流层风速引起的谱线中心波数的频移量极小，直接测量非常困难。因此，采用干涉光谱的方法，利用干涉图的相位变化δφ与风速v的定量关系计算风速，即

式中，τ表示干涉仪采样光程差。

氧气A 带谱线由氧气分子磁偶极矩转动跃迁形成，表现为分布规则的双峰结构，如图1（a）所示。为了精确测量大气风速引起的多普勒频移，需要选择独立性好、吸收强度适中的谱线作为仪器输入，以便于进行滤光片设计、仪器信噪比优化。故选择中心波数在12 999.957 cm-1附近的吸收线作为目标谱线，如图1（b）所示。令吸收谱线函数表达式为

图1 测风目标谱线的选择Fig.1 Target spectrum selection of wind measurement

式中，σ表示入射光波数，σS表示入射光谱中心波数，AS表示吸收率，S0表示入射光谱线最大辐射光强。

星载多普勒差分干涉仪位于地球近地轨道，其轨道高度为580 km，轨道倾角为57°，采用临边观测模式对0～20 km 大气风场进行观测，如图2 所示。仪器沿切线方向进行切片式探测，视线路径距地表最近高度为切线高度，在一次扫描结束后调整切高，进行下次扫描，如此反复直到切线最高处，拥有很高的垂直分辨率［14-15］。

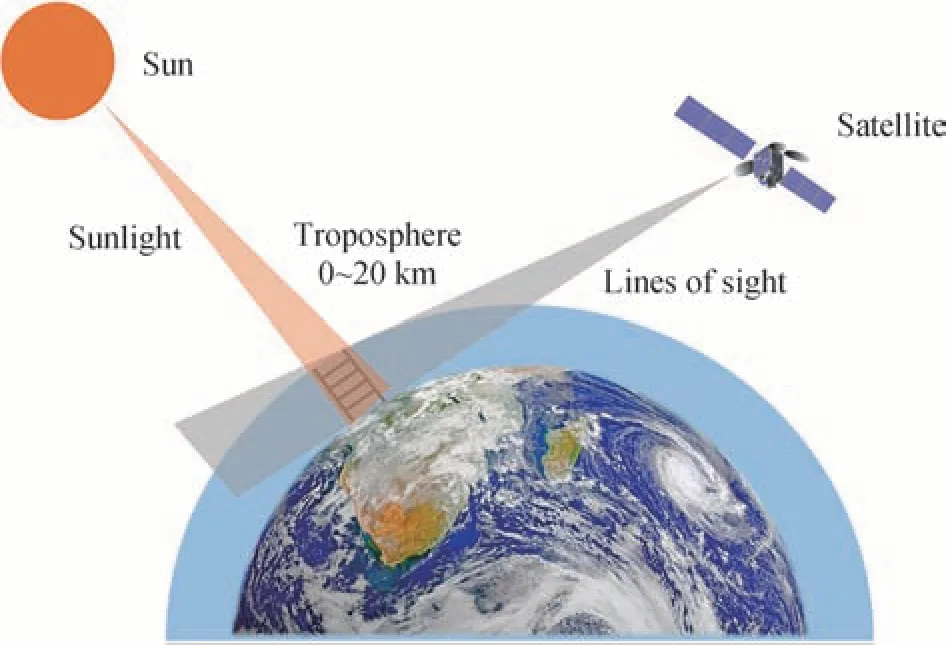
图2 临边观测示意图Fig.2 Schematic diagram of limb viewing

基于多普勒差分干涉仪的对流层风场探测仪器示意图如图3 所示，整个光学系统由望远系统、滤波系统、干涉仪组件三部分组成。大气中散射的光经望远系统收集，通过滤波系统获得目标谱线，之后光经分束镜进入到两臂光路内，再经各自所在光路光栅衍射后返回，在定域面处形成Fizeau 干涉条纹，最后通过条纹成像镜将干涉条纹成像到探测器上。

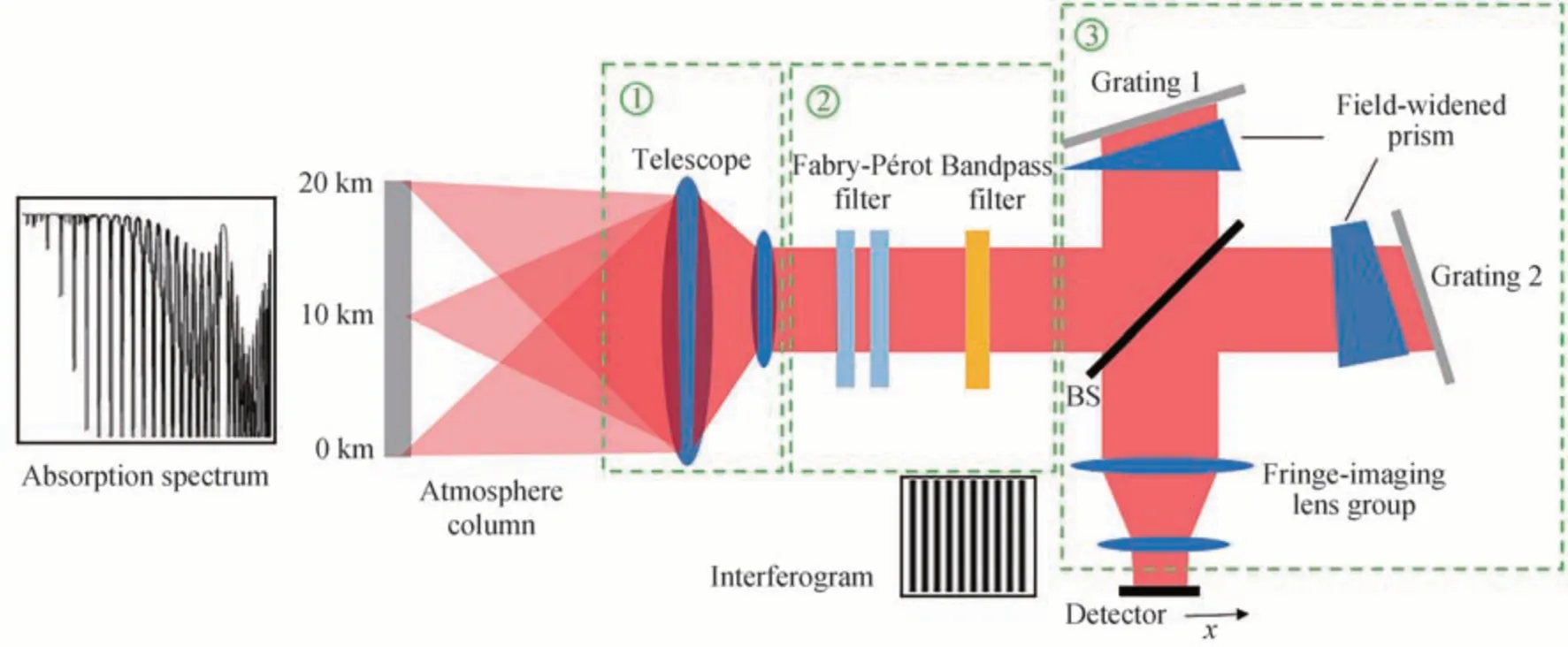
图3 基于多普勒差分干涉仪的风场探测仪器示意图Fig.3 Schematic diagram of wind field detection instrument based on DASH

干涉仪采用多普勒差分干涉仪，结构与Michelson 干涉仪相似，差异在于其将两臂的反射镜替换为与光轴有一定夹角的闪耀光栅，同时在其中一臂光路中增加非对称量使两臂到分束镜间距离不等，从而引入一个大的基础光程差，提高了相位灵敏度［16-17］。多普勒差分干涉仪的干涉条纹表达式为［18］

式中，B(σ)表示入射到干涉仪内的光谱函数，∆d表示单臂非对称量，σL和θL分别表示Littrow 波数和Littrow角，x表示探测器的位置坐标，x=0 表示探测器的中心位置。

2 正演和反演数理基础

在大气光学遥感中，正演模型是描述仪器光学成像过程的数值模拟模型，通过将大气和光源的物理化学性质、仪器参数等代入模型中，经过模拟计算得到预期的原始数据。反演理论采用一个能描述系统行为的理论模型去拟合系统本身的观测，从采集到的原始数据中提取大气物理或化学参量信息。对流层风速的准确探测需要建立基于多普勒差分干涉仪的全链路正演理论模型，并在此基础上进行反演模拟，确保风速测量的准确性。

2.1 全链路正演理论模型

大气辐射传输链路框图如图4 所示，入射到地球大气层中的太阳光经氧气分子吸收、散射后沿临边观测路径入射到系统入瞳，然后经过Fabry-Pérot 滤光片和带通滤光片滤波，最后通过多普勒差分干涉仪在探测器上形成干涉条纹。由图1 可见，氧气A 带的吸收谱线十分密集，12 999.957 cm-1处目标谱线与周围最邻近谱线的距离仅为2 cm-1，将目标谱线从复杂的光谱中提取出来是风场探测的重要前提。Fabry-Pérot 滤光片因其滤波函数的尖锐性，适合对谱线进行精细滤波，但同时因为Fabry-Pérot 滤波函数的图像是一个梳状结构，所以在滤波过程中，除了获得所需部分的窄带谱线外，其他梳齿部分也会对目标谱线区域外进行滤波，获得其所在波数区域的窄带谱线，从而引入杂光。为消除这一影响，增加带通滤光片进行联合滤波，将目标谱线周围的其他梳齿部分滤掉，从而确保滤波后的谱线仅保留目标谱线部分。

图4 辐射传输链路框图Fig.4 The flow chart of atmospheric radiative transfer

Fabry-Pérot 标准具通常用于研究谱线精细结构，具有很高的分辨率，可以产生十分细而亮的等倾干涉条纹。当用作滤光片时，主要利用平行平板的多光束干涉原理，不考虑滤光片缺陷因子，Fabry-Pérot 滤波函数fFP(σ-σF)为

式中，F表示精细度系数，与标准具两平板间的反射率有关，影响到条纹的尖锐度和对比度，n表示两板间折射率，h表示两板间距离，σF表示谱线中心波数，θ表示光在两板间反射时的夹角，δ表示相邻两光束光程差引起的相位差，当δ=2mπ（m=0，±1，±2，…）时，函数会出现峰值。即可以通过设定Fabry-Pérot 标准具两板间的距离或者调整两板间反射率等改变Fabry-Pérot 滤波函数的滤波特性。

单一Fabry-Pérot 滤光片的滤波函数具有周期性，其探测谱线会受到自由光谱区的限制。HRDI 采用三个分辨率不同的标准具依次排列来消除这一影响，从而起到消除杂波的作用，但这种设计对滤光片的加工精度要求较高。本文在单一Fabry-Pérot 滤光片的基础上添加带通滤光片进行联合滤波，使带通滤波函数的带宽与Fabry-Pérot 滤波函数的自由光谱范围大小相当，可以在实现滤波作用的同时降低加工难度。

带通滤波函数G(σ-σG)通常使用高斯函数表示，即

式中，σG表示高斯谱线中心波数，FWHM 表示谱线半波带宽。

Fabry-Pérot 滤光片和带通滤光片的参数如表1 所示。对于氧气A 带吸收线的滤波过程如图5 所示，其中黑色实线和虚线分别代表施加风速前后的氧气A 带谱线，蓝色线表示Fabry-Pérot 滤波函数，绿色线表示带通滤波函数，为了清楚表示滤波过程，图中施加的频移量很大，远大于对流层风速引起的谱线频移。滤波结果如图6 所示，黑色实线和红色虚线分别代表施加风速前后谱线滤波的结果。

表1 滤光片设计参数Table 1 Filter design parameters

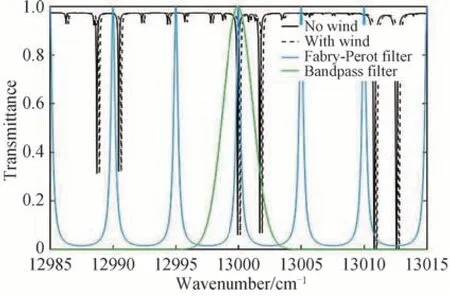
图5 滤波过程模拟Fig.5 Simulation of the filtering process

图6 通过滤光片获得的窄带吸收光谱Fig.6 Narrow-band absorption spectrum obtained through the filters

在不考虑噪声的情况下，采用图6 所示的滤波后的光谱以及表2 所示的多普勒差分干涉仪参数，对施加风速前后的理想干涉图进行模拟，干涉图表达式为

表2 多普勒差分干涉仪主要参数Table 2 Principle parameters of DASH

式中，fx=4(σ-σL)tanθL/β，表示探测器上的条纹空间频率，β表示条纹成像镜的放大倍率。模拟结果如图7所示，黑色实线和红色虚线分别代表施加风速前后的干涉图，因为对流层风速较小，为清楚表示风速引起的干涉图相位变化，对干涉图做局部放大显示。

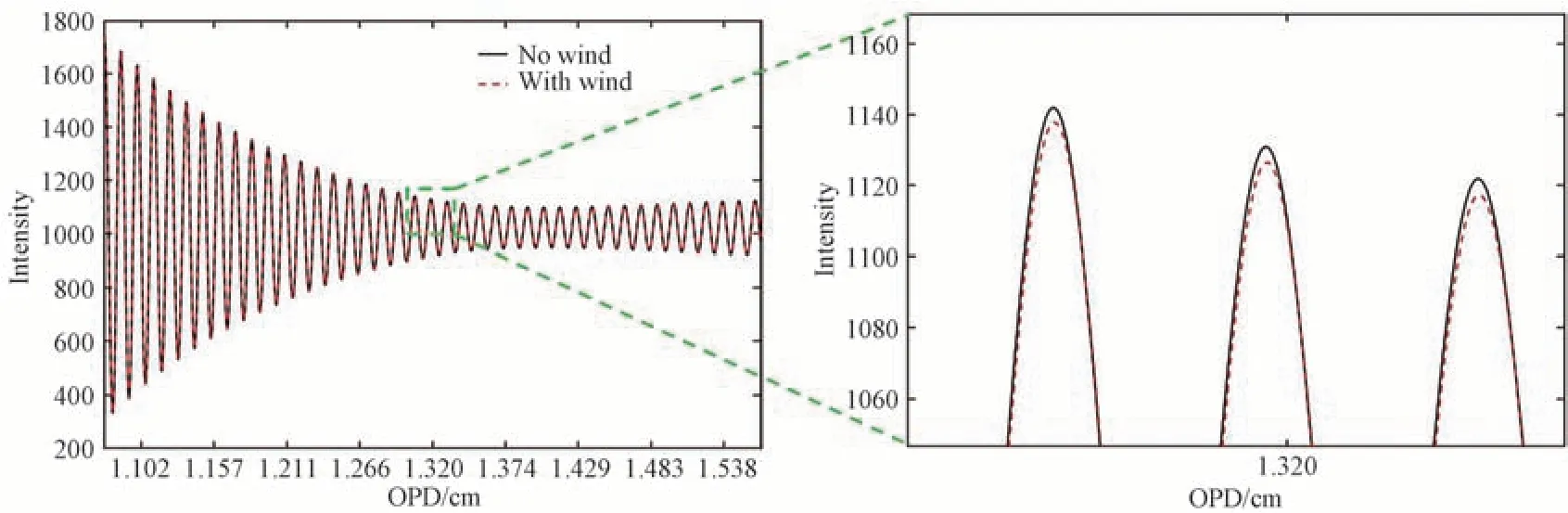
图7 干涉图的相位移动Fig.7 Phase shift of interferogram

2.2 风速反演理论模型

目标谱线经大气传输后在多普勒差分干涉仪的探测器上形成干涉图，通过干涉图的相位变化可获得大气光谱的多普勒频移，进而反演出沿观测视线方向的风速。对于吸收光谱的风速反演，除了分析吸收光谱性质外，还要考虑滤波函数fFP(σ-σF)G(σ-σG)的叠加，这与发射光谱在风速反演上存在不同。基于发射光谱的常规大气风速反演过程主要包括傅里叶变换、单边谱线提取、傅里叶逆变换、实虚部比值求相位。对于吸收谱线，如果采用常规反演方法，单边提取的吸收峰所对应的谱线能量微弱，不利于进行风速反演。

使用与干涉图频率相同的两个正交谐波进行相位解调，该方法不需要进行傅里叶变换，可直接通过对干涉图数据进行处理获得施加风速前后干涉图相位差，从而求解出风速，同时该算法只需要进行一次乘法计算，可以快速实现风速反演。干涉图干涉项为

式中，A表示干涉强度，k表示干涉图空间频率，Φ表示相对相位。取与干涉图频率相同的两个正交谐波信号，用于相位解调，即

式中，MC和MS表示空间频率相同的余弦信号和正弦信号，B表示两束输入信号的振幅，将两信号与干涉图数据通过乘法器相乘，并从中提取相位项，运算过程为

考虑到余弦函数在整数个周期或无穷区间内的积分结果为0，可以通过选择整数个周期的探测器像元数令式（10）结果中的第一项为0，仅保留相位项，据此求得相位大小为

式中，N表示取余弦函数整数个周期时的像元数，Ij表示探测器第j个像元处记录的信号强度，MjS和MjC表示探测器第j个像元处记录的谐波信号强度。依次求得相位φ0和φv，将两者作差得到δφ，表示由风速引起的相位变化，即

探测器上条纹空间频率fx与探测波数、光栅Littrow 波数和Littrow 角、条纹成像镜放大倍率有关，光栅和探测器参数、条纹成像镜放大倍率在仪器设计中已经确定，此时主要影响因素是探测波数。如图6 所示，探测谱线光谱范围为12 995～13 005 cm-1，谱段范围很窄，故选择目标谱线波数12 999.957 cm-1所对应的条纹空间频率作为两谐波信号的空间频率。此时探测器上条纹周期数为39.91，当选择探测器像元数为1 488 个时，正好对应29 个整数周期。

基于理想仪器模型和1976 年美国标准廓线，太阳天顶角取值为40°，不考虑云雨、气溶胶、地表反射等的影响。对于对流层中60 m/s 以内的风速反演进行模拟，结果如表3 所示，表中施加风速大小通过谱线数值模拟获得，将其与通过干涉图反演的风速数值相比较，可得风速反演误差在0.2 m/s 以内，该算法所带来的误差相对较小。

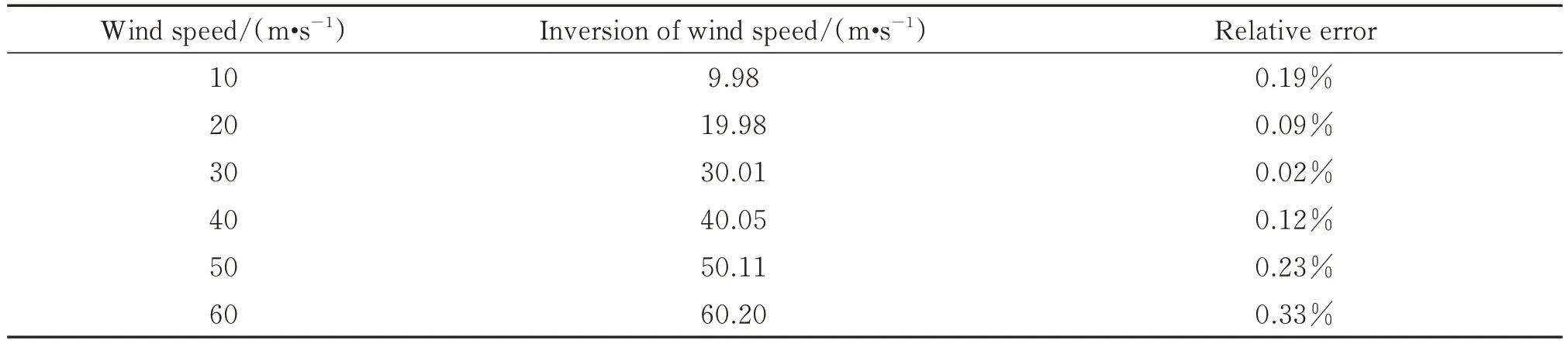
表3 风速反演结果Table 3 Wind speed retrieval results

3 风速测量精度影响因素分析

基于吸收线测风理论，利用多普勒差分干涉仪进行对流层风场探测的测量精度主要受到干涉仪光学参数、滤波参数、系统噪声、仪器稳定性和标准具离轴效应几方面的影响。首先基于风速反演原理分析了多普勒差分干涉仪的非对称量和光谱分辨率对风速测量精度的影响，其次根据吸收线与滤波函数的相互作用关系分析了不同的滤波参数对风速测量精度的影响，最后模拟了不同噪声条件、仪器稳定性和标准具离轴效应对风速测量精度的影响。

3.1 干涉仪非对称量和光谱分辨率

由式（2）可知，干涉仪非对称量∆d越大，干涉图相位对于被测风速的变化越敏感，同时由于谱线展宽会造成干涉图对比度的降低，因此需要合理确定干涉仪的非对称量。对流层内谱线同时受到温度和压强展宽作用的影响，难以通过解析函数确定谱线最优非对称量，此处通过数值模拟的方法确定非对称量大致范围，并在非对称量取6～7 mm 范围内时，对风速反演结果带来的影响进行分析，结果如图8 所示。从图8 中可以看出，风速反演的相对误差随着非对称量的增加先减小后增大。为获取准确的风速反演结果，干涉仪非对称量选取6.5～6.7 mm 时，风速反演的相对误差小于2%。

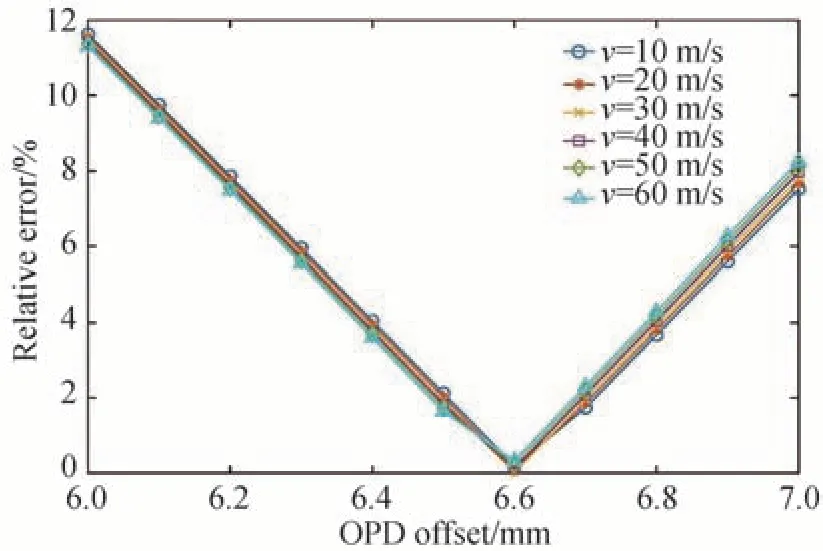
图8 风速反演的相对误差随非对称量变化的规律Fig.8 Relative error of wind speed retrieval as a function of the optical path difference

干涉仪光谱分辨率与条纹成像镜的放大倍率、光栅有效宽度有关，当选定探测器时，光谱分辨率不同，会导致探测器上的条纹空间频率不同，因此会对风速反演的结果造成一定影响，图9 中模拟了干涉仪光谱分辨率变化时的风速反演结果，在光谱分辨率取0.49～0.51 cm-1时，风速反演相对误差小于2%，可见对于仪器光谱分辨率要求较高。

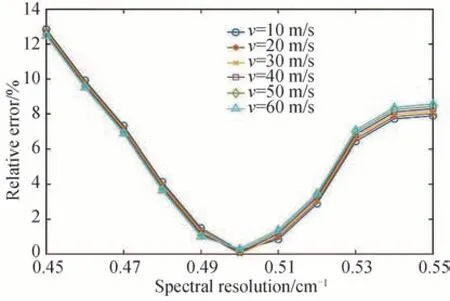
图9 风速反演的相对误差随光谱分辨率变化的规律Fig.9 Relative error of wind speed retrieval as a function of the spectral resolution

3.2 滤光片参数对风速反演精度影响分析

系统滤光片参数的变化会导致滤波函数带宽发生变化，从而导致滤波后的谱线线形发生变化，影响风速反演精度。当带宽较窄时，产生多普勒频移后的谱线可能不在滤波函数范围内，当带宽较大时，可能会引入杂波的影响。基于3.1 节优化结果，分析系统滤光片参数变化对风速反演结果的影响，图10～12 中显示了系统带通滤光片参数以及Fabry-Pérot 滤光片参数变化对风速反演结果的影响。

图10 风速反演的相对误差随带通滤光片半波带宽变化的规律Fig.10 Relative error of wind speed retrieval as a function of the bandpass filter FWHM

图10（a）表示不同带宽下的带通滤光片透过率函数，图10（b）表示带通滤光片带宽对风速测量精度的影响。可见风速测量相对误差随着带宽的增加先减小后增大。考虑到吸收线的谱线展宽，当带通滤波函数带宽较小时，产生多普勒频移后的吸收线光谱范围会超出滤波函数滤波范围，从而降低风速测量精度；当带通滤波函数带宽较大时，引入的杂波会导致风速反演结果不准确。结果表明，带宽取值0.12～0.21 nm 时，风速反演的相对误差在0.6%以内。

图11（a）表示不同标准具间距下的Fabry-Pérot 滤光片透过率函数，图11（b）表示标准具间距大小对风速测量精度的影响。可见风速测量相对误差随着标准具间距的增加先减小后增大。标准具间距的大小与滤波函数自由光谱范围和带宽有关，当标准具间距较小时，可能因为滤波函数带宽较大而引入杂波，从而影响测风精度；而当标准具间距较大时，滤波函数带宽较小，谱线频移后可能不在滤波函数范围内，导致风速反演结果不准确。结果表明，标准具间距取值0.8～1.4 mm 时，风速反演的相对误差在2%以内。

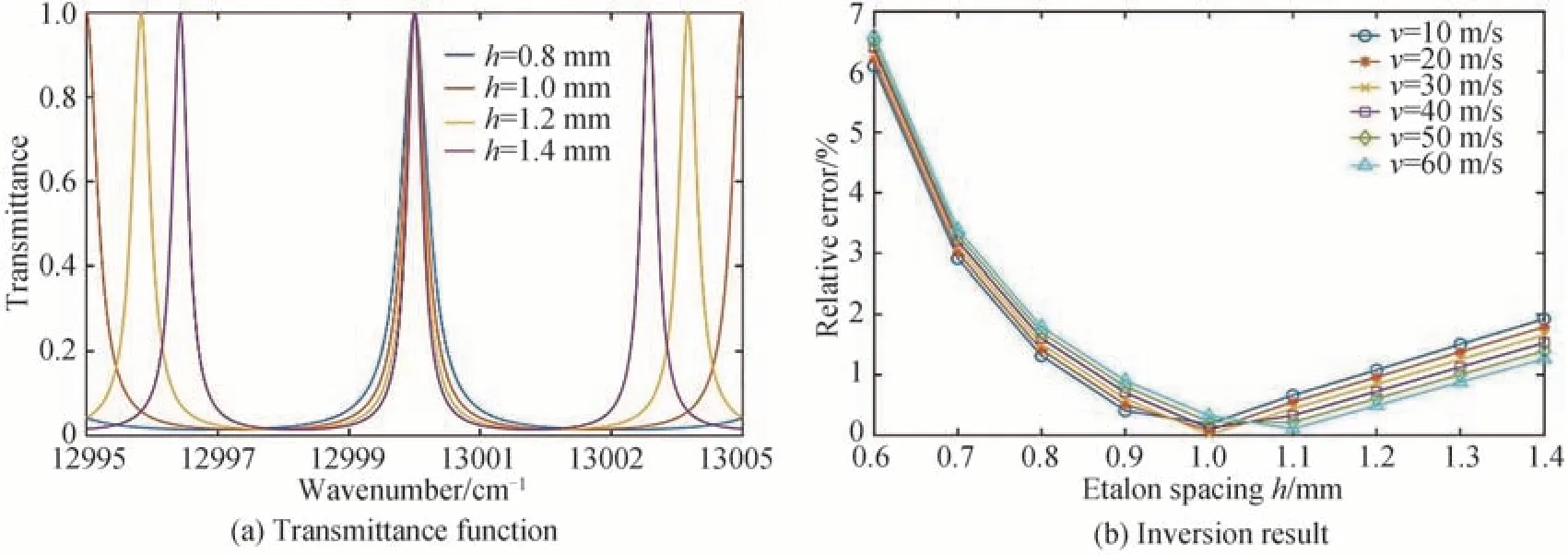
图11 风速反演的相对误差随标准具间距变化的规律Fig.11 Relative error of wind speed retrieval as a function of the etalon spacing

图12（a）表示不同标准具精细度系数下的Fabry-Pérot滤光片透过率函数，图12（b）表示标准具精细度系数大小对风速测量精度的影响。可见风速测量相对误差随着精细度系数的增加先减小后增大。精细度系数代表滤波函数的尖锐程度，精细度系数越大，滤波函数线形越尖锐。当精细度系数较小时，滤波函数较宽，引入杂波会导致风速反演结果不准确；当精细度系数较大时，滤波函数尖锐，产生多普勒频移后的吸收线光谱范围会超出滤波函数范围，从而降低测风精度。结果表明，精细度系数取值30～100时，风速反演的相对误差在2%以内。

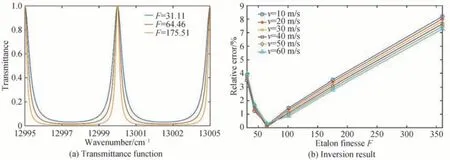
图12 风速反演的相对误差随标准具精细度系数变化的规律Fig.12 Relative error of wind speed retrieval as a function of the etalon finesse

3.3 信噪比对风速反演精度影响分析

基于3.1 节和3.2 节优化结果，分析在多普勒差分干涉仪成像过程中的噪声影响。采用干涉图信号与噪声功率比值作为信噪比，假设原始干涉图以光子噪声（属于高斯白噪声）为主要噪声源，对干涉图施加10～100 倍信噪比，并各自进行10 000 次风速反演模拟，计算10 000 次反演结果均值与施加风速大小的相对误差，如图13 所示。结果表明，干涉图信噪比增大可以提高风速反演精度，在信噪比大于40 倍时，风速反演最大误差优于2 m/s。

图13 风速反演的相对误差随信噪比变化的规律Fig.13 Relative error of wind speed retrieval as a function of the SNR

3.4 仪器稳定性对风速反演精度影响分析

对于多普勒频移探测而言，仪器稳定性是精确测量的基础，此处对法布里-珀罗标准具和干涉仪的稳定性要求进行分析。

法布里-珀罗标准具对温度的变化比较敏感，由于材料热膨胀和折射率温度效应的影响，光程会随着温度发生变化，从而导致透射峰的波长随温度变化发生漂移，影响风速反演的准确性［19］。图14 模拟了透射峰偏移时风速反演的相对误差。结果表明，风速反演相对误差随着透射峰偏移量增大而增大，当透射峰偏移量小于0.018 cm-1时，风速反演误差在5 m/s 以内，可见对标准具稳定性具有很高的要求。

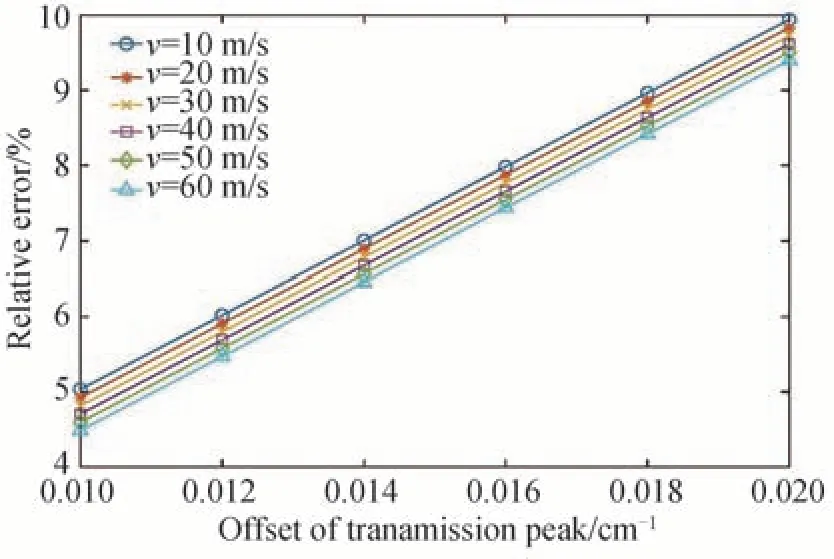
图14 风速反演的相对误差随透射峰偏移量变化的规律Fig.14 Relative error of wind speed retrieval as a function of the offset of transmission peak

干涉仪基准相位的稳定性直接影响到风速测量精度，基准相位的漂移主要受到仪器光机系统热特性的影响，可分为相位斜率漂移、干涉图相位漂移和非对称量相位漂移三部分。相位斜率漂移指条纹空间频率和成像系统放大倍率随温度发生变化，通过计算干涉条纹相位随探测器采样位置变化的线性函数斜率可实现相位斜率漂移的获取。干涉图相位漂移由干涉仪和探测器在热环境下相对位置的变化引起，指干涉图像整体的漂移，通过监测连续两帧图像亚像元的位移量可实现干涉图相位漂移的获取。非对称量相位漂移是指干涉仪非对称量随温度发生变化，从而导致干涉仪基础光程差发生变化，通过在总体相位漂移中减去相位斜率漂移和干涉图相位漂移，可实现非对量相位漂移的定量获取。通过对各相位热漂移进行定量计算，可确保总体的稳定性，同时有利于开展硬件优化设计［20］。

3.5 标准具离轴效应对风速反演精度影响分析

以上分析均基于轴上情况，实际标准具的透射函数与入射角θ有关，其入射角通常称为离轴角。在轴上风速反演最优的情况下，分析离轴角对风速反演的影响。滤波函数的带宽会随着离轴角的增大而增大，同时透过率会随着离轴角的增加而减小，因此在滤波过程中可能会引入杂波，从而影响风速反演结果［21］。

卫星轨道高度为580 km，地球平均半径为6 371.393 km，计算得空间高度20 km 处视线风所对应系统半视场角为0.2°，故分析0.2°以内离轴角对风速反演结果的影响。图15（a）表示不同离轴角下标准具的透过率函数，图15（b）表示离轴角对风速测量精度的影响，风速反演精度随着离轴角增大而逐渐降低。结果表明，当离轴角取值在0.2°以内时，风速反演最大误差优于8 m/s。

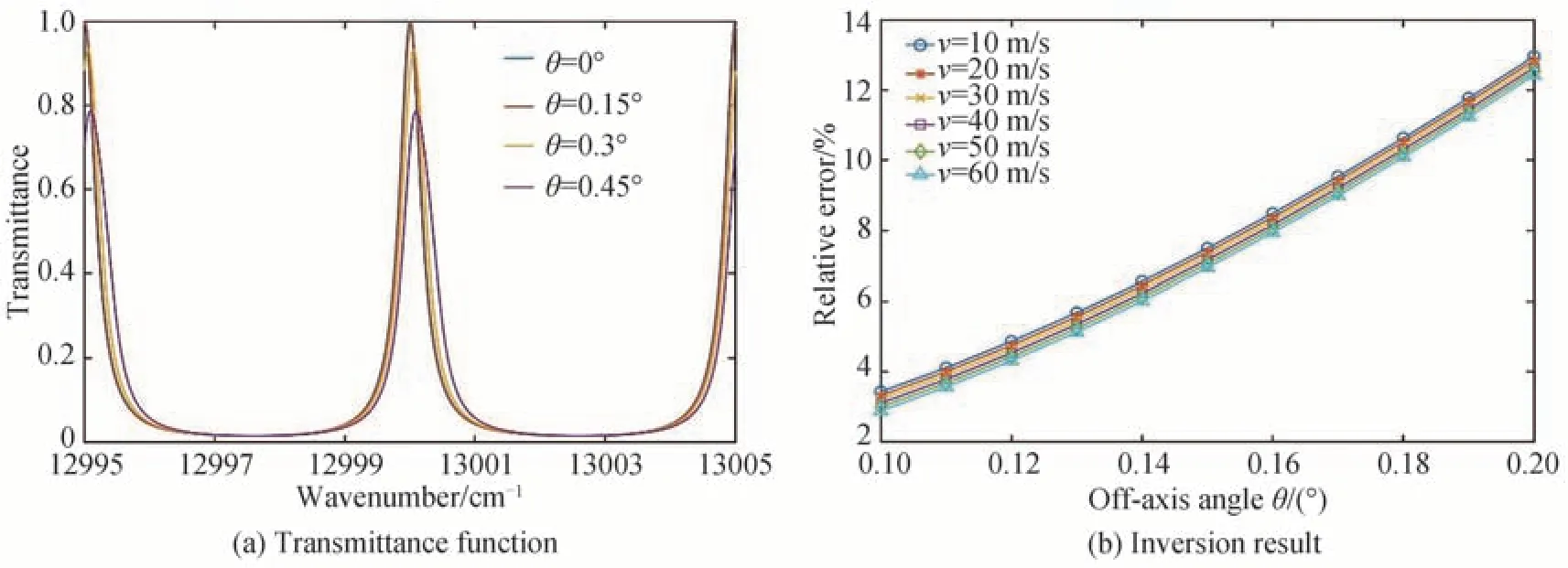
图15 风速反演的相对误差随离轴角变化的规律Fig.15 Relative error of wind speed retrieval as a function of the off-axis

4 结论

基于氧气A 带吸收线测风理论，证明了基于多普勒差分干涉仪进行对流层风场探测的可行性。通过分析各影响因素对风速反演结果的影响，确定光学系统参数最优取值范围。结果表明，风速反演相对误差随干涉仪非对称量和光谱分辨率的增加先减小后增大，同时对干涉仪的稳定性具有很高的要求，风速反演相对误差随带通滤光片带宽、标准具两板间距和精细度系数的增加而先减小后增大，随标准具透射峰值偏移和离轴角的增加而减小，风速反演相对误差随信噪比的增加而减小。综合考虑各影响因素，风速反演结果在8 m/s 以内。本文针对单一空间高度层目标谱线信息进行风速反演研究，但不同空间高度上目标谱线信息不同，仪器参数的最优取值范围也会略有不同，该问题将在后续工作中进一步研究。研究结果可为开展相关仪器的设计和研制提供理论依据。