基于外置光阑针孔相机的高精度偏折测量技术

叶璐，张祥朝，王军华，徐敏，郑列华

（1 复旦大学 上海超精密光学制造工程中心，上海 200438）

（2 中国科学院上海技术物理研究所，上海 200083）

0 引言

随着光学系统分辨率不断提高，光学镜面面型的复杂度和加工精度要求也随之提高，从而导致检测难度大、检测时间长。传统的非球面检测方法［1，2］可以分为点扫描检测法和干涉检测法两大类。光学非球面通常在研磨阶段采用以三坐标为代表的驻点扫描三维轮廓测量，此方法检测时间长、成本高、被测镜的大小受限于测量仪器的结构尺寸。在光学加工的抛光阶段，通常采用高精度的干涉测量法，但也存在着弊端。由于干涉量程的限制，不同参数的非球面需要一个特定的零位补偿器［3］辅助测量，导致测量成本高，并且对于非球面度比较大的情况，全口径出光较难。尤其是研磨阶段到抛光阶段的过渡测量，现有方法均无法同时满足测量精度和动态范围的要求。

偏折测量技术是近年来新兴的三维光学检测技术。该方法将特定编码的图样显示在屏幕上，用相机记录被测面反射的图像，进而重构被测面的三维形貌。国内四川大学［4］、长春光机所［5］、复旦大学［6，7］等都对该技术展开了全方位的研究，并实现了多种镜面物体的测量。国外，SU P 等［8，9］提出了基于相位测量偏折术的软件配制光学检测系统（Software Configurable Optical Test System，SCOTS），目前有报道显示他们已成功将SCOTS 运用于巨型麦哲伦（Giant Magellan Telescope，GMT）主镜子镜（RMS 为0.4 μm）的检测。

偏折测量具有动态范围大、抗噪能力强、测量速度快、硬件成本低的优势，且不存在干涉测量的量程限制问题，能明确指导修正加工，减少面型迭代次数，因此适用于车间中的复杂工况测量。但是偏折测量又有其自身的局限性，测量精度直接依赖于系统中各个元件相对位置的计算准确性，即几何标定精度。偏折测量通常将相机视为针孔相机模型，拍摄标定板在不同位姿下的图片，通过张正友标定法［10］获取相机内参和外参，通过软件计算获取相机CCD 上每个像素的坐标。传统的相机标定方法过程复杂，受标定板精度的影响较大，并且相机标定和几何标定一般是分别获得的，坐标系的转换过程中也会存在误差的传递和耦合。大多数工业相机镜头为了消除像差采用对称结构，孔径光阑位于镜组中间，为了直接获得相机光阑中心坐标（也叫光心坐标），需在镜头前添加外置光阑，虽然可以直接通过测量获取光心坐标，可是会影响相机的视场角，给测量带来不便。偏折测量需要一个理论曲面模型来估计整个表面的测量点的位置，一般的初始模型为了方便计算采用平面模型或者球面模型，但是不确定的表面模型往往对计算法线产生较大的误差，从而影响测量精度［11，12］。

为了解决以上问题，本文提出了一种针孔相机镜头的设计方法，能够快速、准确的获取光心坐标并可以实现简单便捷的反射光线标定，适用于多种应用场景的标定。

1 基本原理

偏折测量技术是一种获得光学表面斜率的方法，测量原理图如图1 所示，液晶显示器（Liquid Crystal Display，LCD）显示编码的结构光图样，相机采集经过镜面反射后畸变的条纹，根据反射定律，入射光线和反射光线的角平分线为镜面被测点的法线，进而得到被测镜表面的梯度，而表面面型可通过表面斜率积分来拟合重构。

图1 偏折测量原理图Fig.1 Diagram of deflectometric measurement

由光线的反射定律，可以得到关系式［8，9］

式中，（xc，yc，zc）为相机光心坐标，由几何标定获得；xm和ym为被测点的横坐标，由每个相机像素与光心相连所得反射光线与待测表面计算交点得到；（xs，ys，zs）为对应的屏幕像素坐标，可以通过相移算法获得；dm2s和dm2c分别为被测点到屏幕像素点和被测点到相机光心的空间距离，也是通过精确的几何标定来获得；W(xm，ym)实际上是未知的，初始值由理想的设计参数代替，在迭代过程中替换为当前重构的值；gx(xm，ym)和gy(xm，ym)是测量得到的被测点在x和y方向上的斜率。

如果光源为LCD 屏投射四步相移条纹，偏折术测量系统的分辨率［13］表示为

式中，Δz为偏折测量系统的z坐标分辨率，NA 为相机的数值孔径，Δφ为相位分辨率，文献［13］给出经验值为2π/400，xpix为相机像素大小，对于像素尺寸为7 μm 和F#为2 的相机，由式（2）可以计算，系统分辨率约等于4 nm，因此，偏折术测量方法的检测精度可以达到纳米级测量分辨率。

根据图1 的测量原理，可以推导出

式中，Δz为被测点局部的高度变化值，xcam为相机的空间分辨率，即每个像素对应的镜面的大小，tanα为被测点的斜率。外置光阑中心坐标由三坐标测量，测量误差可以控制在0.02 mm 之内，若光阑到被测镜的距离为1 m，镜面分辨率为0.1 mm，则由于光阑位置测量误差导致的被测点斜率偏差为20 μrad，根据式（3），被测点的高度误差为2 nm。

若光阑大小为1 mm，所有进入相机的光线在光阑位置的坐标横向偏差最大为0.5 mm，是测量误差的25 倍，根据上面的推导可以计算出，相机边缘视场的光线由于光阑大小引起的被测点的高度误差为50 nm。因此，可通过增加被测面到相机的距离来提高测量精度。

2 实现过程

2.1 针孔相机镜头设计

本文设计了一款光阑位于镜头外部的可见光相机镜头，这样设计的好处是不仅可以免去商业镜头复杂的相机标定，而且可以通过光阑的物理位置快速获取相机光心坐标，提高光心坐标点的获取精度。通过计算分析，此镜头适用于大多数光学反射镜的偏折测量。实验室原有的一台工业相机，相机参数如表1 所示，相机靶面大小为14.18 mm×10.37 mm，对角线约为17.56 mm。

表1 相机参数列表Table 1 Camera specification list

光学加工车间中常见的反射镜F#一般大于1.3，为了减小所需屏幕的尺寸，在偏折测量光路中一般将相机放置在被测镜曲率中心附近，通过式（4）计算相机焦距。其中D为被测镜口径，R0为被测镜顶点曲率半径，d为相机靶面大小，f为相机焦距。

相机镜头的像面大小要与相机感光面的大小兼容，尺寸不匹配的话，会影响边缘视场的像质。在这里设计相机镜头焦距为22 mm，视场角±15°，基本满足本实验室加工中所有反射镜的偏折测量要求。在光阑前置的设计方案中，光学结构失去对称性，导致像差矫正困难，最终优化结果为四片式结构，其中一片为双胶合镜片，需要注意考虑相机探测器的保护窗厚度。设计光路如图2 所示。

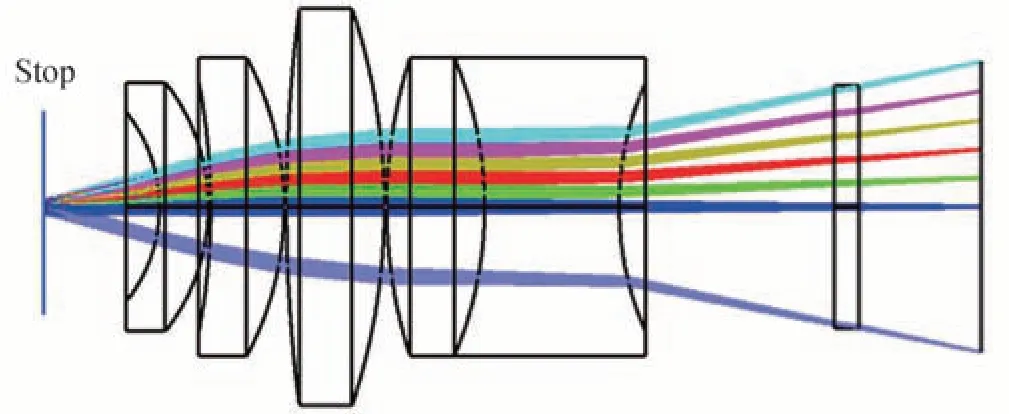
图2 相机镜头光路图Fig.2 Camera lens layout

光阑位于第一片镜片之前4 mm 的位置。改变光阑的大小不影响镜头的视场角，仅仅改变入射到镜头内部的光通量。

镜头系统的点列图如图3 所示，随着光阑口径缩小，屏幕的分辨力得到提升，即数值孔径越小景深越大，有利于保证条纹成像的清晰度，这对测量是有利的，但是同时，光阑口径减小，光通量随之减小，造成图像信噪比的下降，而通过额外的照明来增加光通量，则会导致产生杂光，影响面形的重构精度。因此，实验中在不过曝的前提下，采用增加曝光时间的方法来改善图像清晰度。

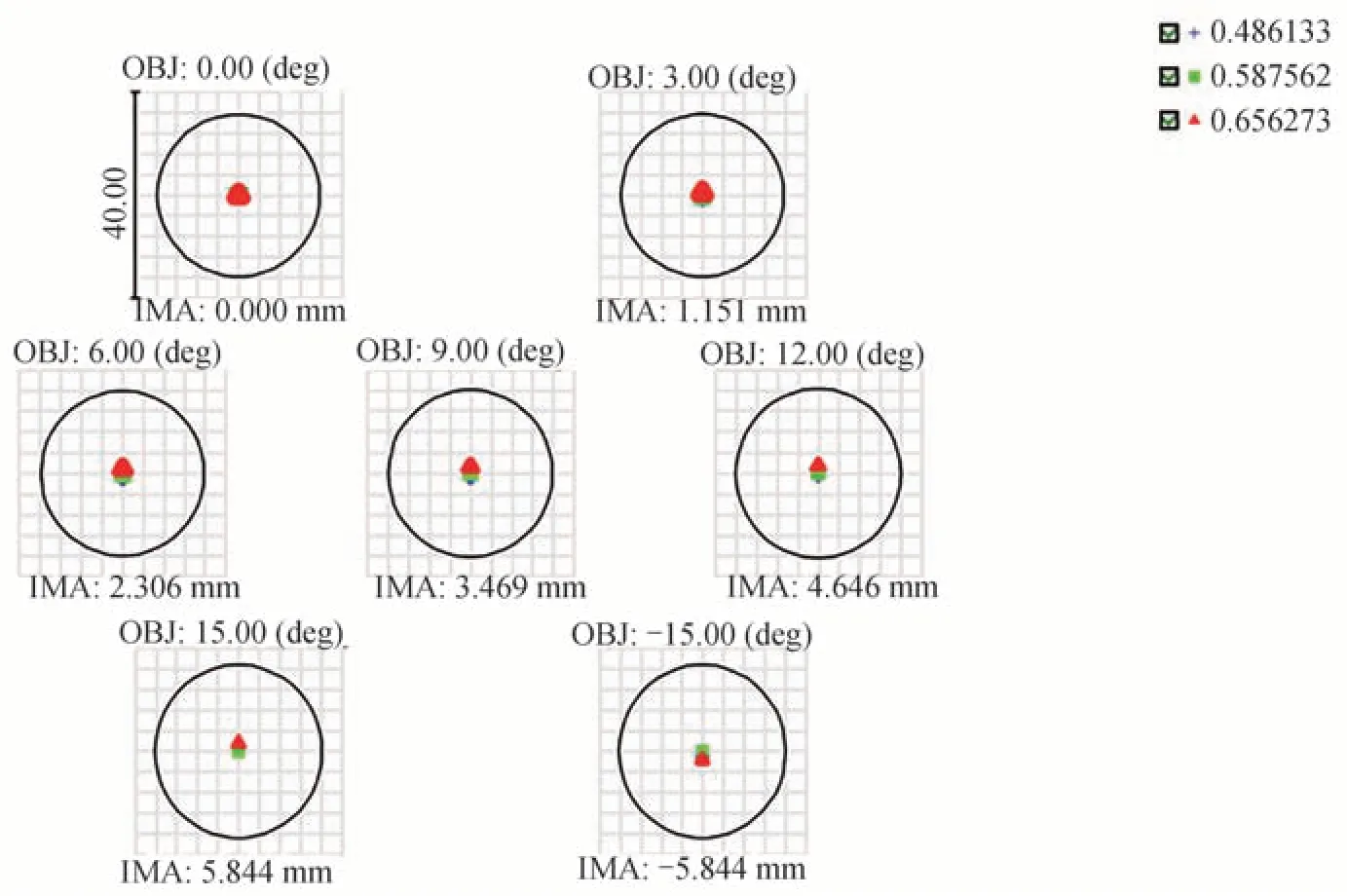
图3 相机镜头点列图Fig.3 Camera lens standard spot diagram

镜头的成像质量好坏是指显示图样能否清晰成像或者有没有失真情况，当各视场的弥散斑面积均小于艾里斑时，表明系统具有较高的成像质量，偏折术中主要关注镜头的畸变，一般的商业镜头畸变小于2%，并且畸变可通过相机标定及软件算法进行后期补偿，这里的光学系统畸变设计值为0.707%，如图4 所示，可以满足使用要求。

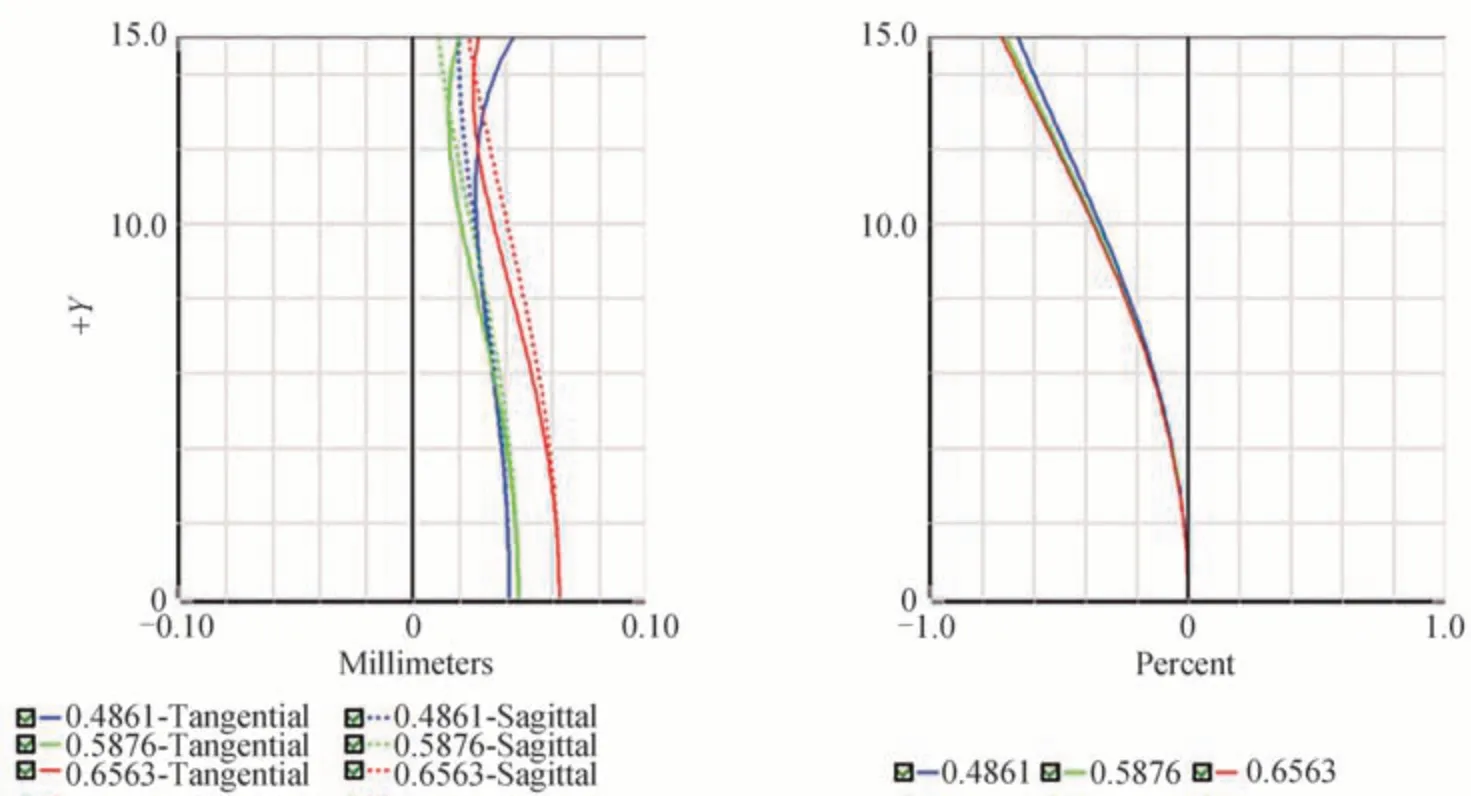
图4 相机镜头畸变Fig.4 Camera lens distortion

镜头的机械结构如图5所示，在镜头的最前端做一个可更换光阑的螺纹结构，方便更换不同大小的光阑，光阑的外形设计为一个较长的圆柱，方便采用三坐标或者激光跟踪仪等外部测量设备获取光阑中心坐标。根据被测镜的参数不同，相机的工作距离也有相应的调整。小于最小工作距离或大于最大工作距离的系统一般都不能清晰成像，设计调焦结构，使镜头组与相机感光面之间可通过螺纹结构调节，来适应不同曲率的被测镜。

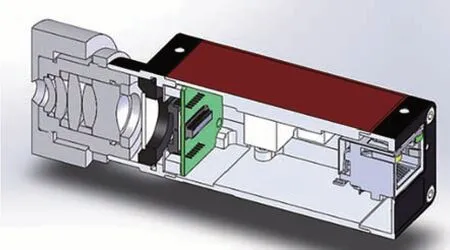
图5 相机结构模型Fig.5 Camera structure model diagram

2.2 几何标定

如图1 所示，偏折测量系统的几何标定主要是确定相机、屏幕以及被测镜之间的相对位姿关系，并且将三者统一至以被测镜中心点建立的世界坐标系中。规定坐标系的转换均使用右手坐标系，其中固定一个旋转轴，旋转方向从固定轴的反方向观察，顺时针为旋转逆向，逆时针为正向。

若坐标系绕着X轴旋转角度θx，绕着Y轴旋转角度θy，绕着Z轴旋转角度θz，则坐标系转换前后的关系可以用式（5）和式（6）来表示。

以罗德里格矩阵的变换理论为基础［14］，任意两个坐标系之间需要已知三个不共线的点坐标，即可完成坐标系之间的转换，在被测镜工装上添加标志物，用三坐标或激光跟踪仪等外部设备测量标志物的几何位置，构建出空间三个不共线的点坐标。相机光心坐标可通过外置光阑直接确定，屏幕坐标通过影像仪获取，依靠已知点的像素坐标转换至工件坐标系，使屏幕和相机都转换至工件坐标系下，实现坐标系的统一。

2.3 反射光线标定与被测点求解

为了标定相机光线方向，即测量光路中反射光线的方向，本文采用一种简单便捷的方法，运用高精度的相移算法来确定反射光线方向，原理如图6 所示。

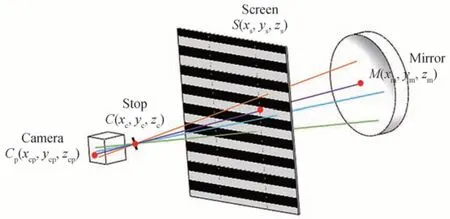
图6 光线方向标定Fig.6 Calibration diagram of rays

反射光线求解过程如图7 所示。

图7 反射光线与被测点的求解过程Fig.7 The calculating process of reflected rays and measured points

相移法计算的相位值在( -π，π)之间折叠，并不是真正的相位，采用相位展开算法，可得到连续光滑的相位值，本文采用标志点的方法，从标志点的像素点开始遍历，比较前后两个相位值的大小，如果前后相位之差超过π，则说明出现了截断相位，判断条纹周期k，再加上或减去2kπ 使其回归到真实周期。

测量光路中每一个相机像素对应的光线方向可以用式（7）来表示。

式中，xc，yc，zc为相机光阑中心坐标，xs，ys，zs为每一个相机像素对应的屏幕像素坐标，l，m，n为每一个相机像素对应的方向向量，代表了反射光线的方向。

由空间直线对称式方程很容易导出空间直线参数方程，由式（8）表示，其中t为参数。

每一个相机像素对应的反射光线可表示为

若被测面为二次非球面，则被测面可以表示为

式中，c=1/R0，R0为非球面顶点曲率半径，k为非球面二次曲率系数，联立式（9）和式（10），有

从式（11）可看出t为一元二次方程的解，将t代入式（9），即可求出每一个相机像素对应的被测点坐标矩阵。

空间光学系统中，由于离轴反射系统无色差、无遮拦的优点，大口径的离轴反射镜常常出现在光学加工车间，对此类镜面面型，无法用简单的表达式来表示，因此被测点坐标的计算难度增大，若用平面或球面模型，导致计算法线的误差较大，影响面型重构精度。离轴非球面的坐标系XYZ和母镜坐标系X′Y′Z′之间的关系如图8 所示。

图8 离轴非球面的坐标系Fig.8 Coordinates of off-axis aspheric surface

通过公式推导［15］，离轴反射镜面在坐标系XYZ中的表达式可以表示为

令a=1+ksin2θ，b=1+kcos2θ，代入式（9），可得

从式（13）可看出t为一元二次方程的解，将t代入式（9），即可求出每一个相机像素对应的被测点坐标矩阵。此公式推导为被测点坐标的精确解，有利于重构精度的提升。

3 实验验证

实验中被测镜为一个凹抛物面铝镜，由单点金刚石车床加工，口径为110 mm，曲率半径为800 mm，屏幕为7.9 英寸（1 英寸=2.54 cm）的iPad mini2，屏幕分辨率为2 048×1 536，相机型号为Manta G-1236，分辨率为4 112×3 008，像素大小为3.45 μm×3.45 μm，镜头焦距22 mm，光阑直径为1 mm，偏折测量实验装置如图9 所示，相机和屏幕分别放在被测镜曲率中心附近，调焦使相机采集的条纹具有清晰的对比度。

图9 实验装置Fig.9 Experimental setup

用影像仪标定屏幕像素坐标系下的像素坐标以及屏幕工装坐标系下的像素坐标，如图10 所示，通过第2.2 节的坐标转换公式，通过点亮已知像素并测量在屏幕像素坐标系与屏幕工装坐标系的坐标值，即可计算两个坐标系之间的旋转矩阵和平移向量，实现坐标系的转换。如图9 所示，镜子工装上安装了3 个发黑的铝块，作为参考点，用三坐标测量工件坐标系下三个铝块的坐标值以及屏幕坐标系下三个铝块的坐标值，确定两个坐标系之间的变换关系，相机光心坐标可以直接测量获得。

图10 屏幕像素坐标标定Fig.10 Calibration of screen pixel coordinates

相机采集经过被测镜反射的畸变条纹后，用三坐标进行高精度的几何标定，将屏幕移至相机与被测镜之间，如图11 所示，按2.3 节中的方法标定光线的反射方向，并求解被测点坐标。

图11 反射光线方向的标定Fig.11 Calibration of reflected light direction

将以上步骤获得的数据代入式（1），求得被测点x和y方向的斜率，采用区域波前重构获得被测镜的表面面型。图12 对SCOTS 法的面型重构结果进行了详细的对比，和Luphscan 轮廓仪测量结果在一个数量级，面型高低分布也基本相同，面型分布有较大的离焦和像散证明了这些像差为被测镜本身的面型误差而非测量引起的误差，为了进一步对比分析，采用Zygo 干涉仪用平面镜自准的方式来测量抛物面面型，平面镜自身的面形精度RMS 优于1/80λ（λ=632.8 nm），干涉仪采用F数为5.1 的球面镜头，测量光路中平面镜中孔遮拦大小为22 mm，因为干涉仪无法测出光焦度，因此SCOTS 重构数据去除Zernike 项Z1～Z4后，再去除中心22 mm 后与干涉仪数据对比，干涉仪测试RMS 为0.121λ，SCOTS 法重构结果为0.131λ，可以证明，通过高精度的几何标定，偏折测量可以达到干涉仪同等测试精度。

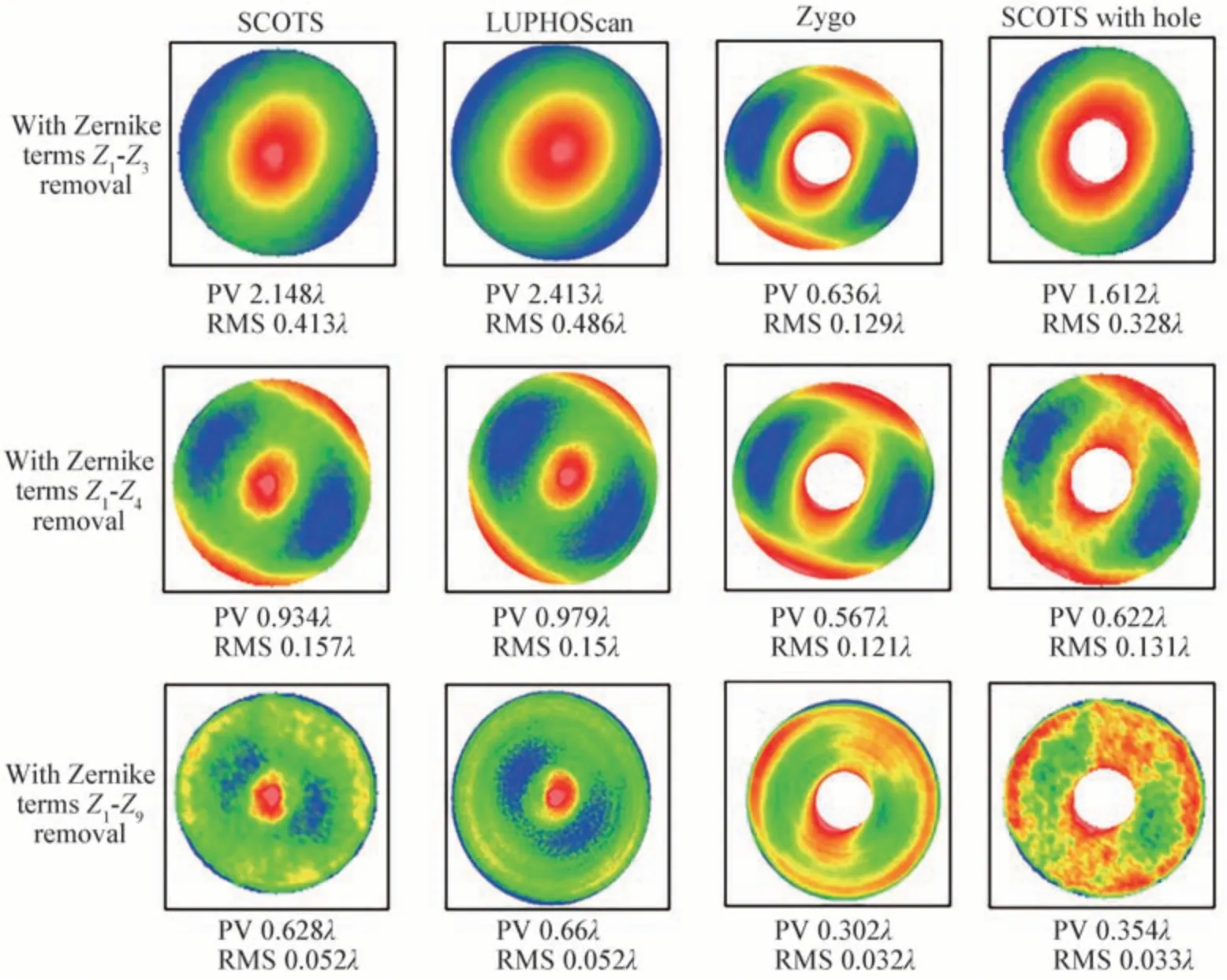
图12 重构结果Fig.12 Reconstruction results

偏折测量数据的重构处理仅仅采用一次面型重构，没有采取迭代算法，证明了反射光线标定的准确性以及被测点求解的准确性，面型重构的结果可以达到和LuphoScan 相当的测量精度，并且可以测量出离焦和像散等低阶误差，说明几何标定精度较高。

为了验证测量精度，采用偏折术的重构结果分别与Luphoscan 和激光干涉仪测试结果逐像素做差，重构误差如图13 所示，均表现为高级彗差。与Luphoscan 的面型偏差为0.043λ（27 nm）RMS，在镜子的中心点面型误差有局部高点，这是因为Luphoscan 测量为螺旋线扫描，最终的面型数据由插值算法获取，在局部陡度位置会产生微量的偏差，面型逐像素做差的过程中由于微量的位置错位导致中心区域误差较大。与激光干涉仪的面型偏差为0.032λ（20 nm） RMS，经分析，偏折术测量光路的基准位于被测镜的顶点位置，而激光干涉仪测量光路中，三维空间的镜面成像到二维的探测器表面，此过程产生畸变，因此采集的面形图基准有可能偏离非球面的顶点，两种测量方法的基准存在偏差，因此导致面型做差产生误差，根据实验结果有理由认为实际上测量误差应该小于20 nm，并且证明此精度不仅可以满足光学镜面从研磨到抛光阶段的测量精度需求，而且可以满足更高精度的测量需求。

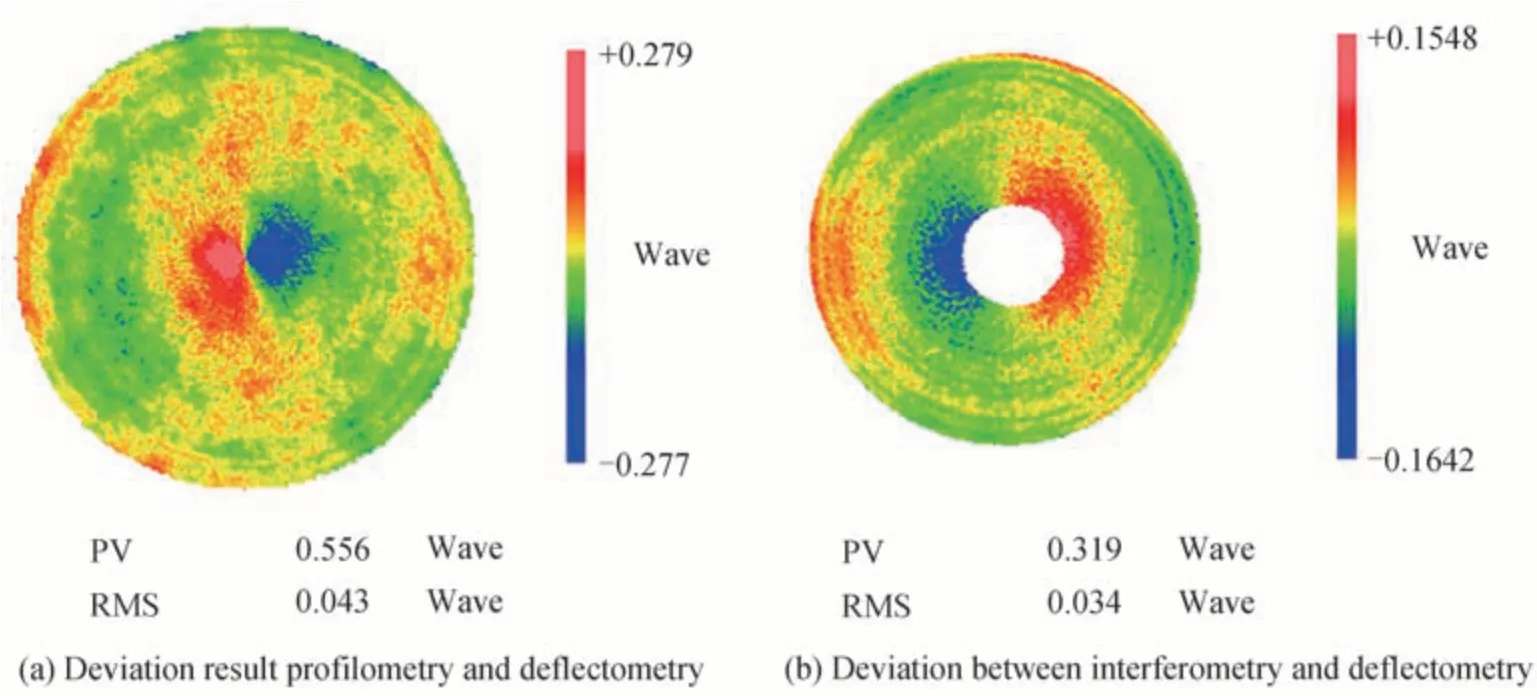
图13 不同测量方法的比较Fig.13 Comparison of different measurement methods

偏折术测量的是待测面的梯度，不受被测镜表面对称性与非球面度的影响，不仅可以测量球面、非球面，也可以测量离轴非球面与自由曲面。为了验证离轴非球面交点公式推导的准确性，采用本次实验测量数据，取镜面离轴区域数据，x方向离轴量设为27.5 mm，离轴区域设为口径50 mm 的圆形区域，找出屏幕像素坐标、计算反射光线的屏幕坐标与被测镜离轴区域一一对应的数据，将坐标系由初始的同轴抛物面的中心转换至被测镜离轴区域中心，采用坐标转换后的相机光心数据和标定反射光线的屏幕数据连线，带入式（12）和式（13）求解离轴抛物面被测点坐标，离轴区域的重构面形如图14（a）所示。同轴抛物面的重构面形取离轴区域后面形如图14（b），两幅图面形分布和数量级基本一致，说明离轴镜被测点求解公式正确。

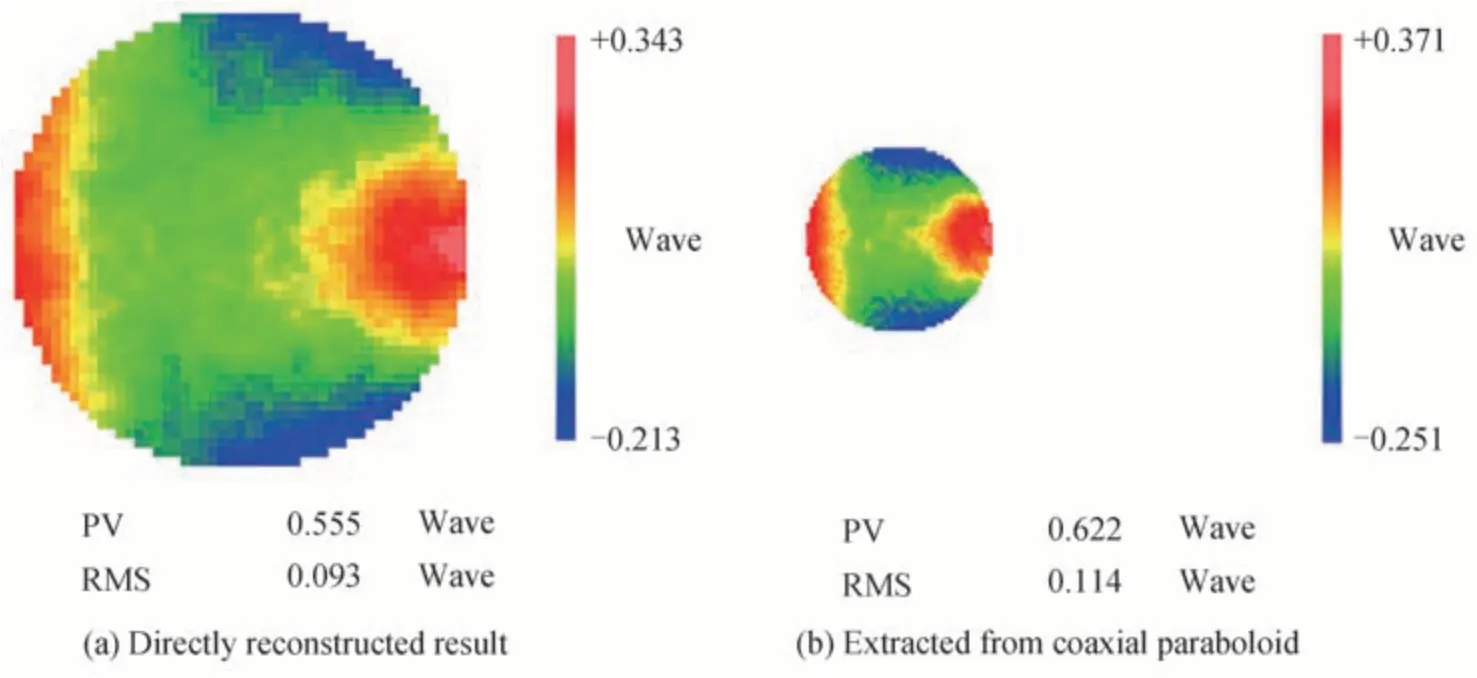
图14 离轴区域重构结果对比Fig.14 Comparison of reconstruction results of off-axis paraboloid

4 结论

本文阐述了偏折测量系统中针孔相机的设计理念和结果，采用光阑中心坐标结合高精度的相移算法来确定反射光线方向，实现了相机校准和几何校准的融合。该方法操作简单、结果可靠、实验数据表明偏折测量精度与干涉测试相当，同时它结合了干涉仪与三坐标各自的优点，可测量球面、非球面、自由曲面等多种面型，且动态范围大、测量速度快、硬件成本低、抗噪能力强，可满足光学车间复杂工况下镜面的测量需求，对光学加工有重要的指导意义。