基于神经网络的短期土壤墒情预测模型研究
杨靖峰, 刘志良, 沈艳妍
(天津市农业发展服务中心,天津 300061)
目前土壤墒情预测模型的研究主要分为2 类。一类是基于土壤水分平衡和土壤水动力学的水理论预测模型,如侯琼等[2]建立了土壤水分动态预测模型来预测内蒙古地区玉米田的土壤墒情;一类是基于数据统计的预测模型,如白冬妹等[3]应用时间序列自回归模型预测土壤含水量,尚松浩等[4]建立了BP神经网络模型预测小麦田墒情。
本研究建立BP 神经网络和Elman 神经网络2种预测模型,用2 组维度不同的数据分别对2 种模型进行训练模拟,旨在找出预测精度更高的短期土壤墒情模型及其有关参数,用于预测1 d(24 h)后的土壤墒情,最终应用于实际农业生产。
1 数据来源与数据处理
1.1 数据来源
研究区域为天津市,该地区主要气候特征是四季分明,春季多风,干旱少雨;夏季炎热,雨水集中;秋季气爽,冷暖适中;冬季寒冷,干燥少雪。2000年以来天津地区的年平均气温为13.5 ℃,最高温度为42.7 ℃,于2017年7月11日出现在静海区,最低温度-22.6 ℃,于2021年1月6日出现在蓟州区;年平均降水量一般在370~750 mm,降水大部分集中在6—9月,但2021年降水量为979.1 mm,创下1961年有气象资料以来最高纪录。
本研究的数据来源于天津市蓟州区、静海区、宁河区、滨海新区的10 个气象墒情自动监测站(表1)。每个站点均可同时监测气象数据和墒情数据,其中气象数据包括空气温度、空气湿度、风速、风向、光照、雨量、蒸发量、大气压力、露点温度、作物蒸腾蒸发量;墒情数据包括土壤体积含水量、相对含水量、温度、盐分,均为20、40、60、80 cm 4 个土层深度数据。数据跨越时间为2018 年9 月1 日—2021 年8 月31 日,监测站每15 min 采集1 次数据。本研究的天气预报数据来源于天津市气象局发布的各区天气预报数据,共1 095组数据。

表1 各气象墒情自动监测站位置
1.2 数据处理
为确保数据有意义且具有可操作性,原始数据在应用前进行完整性检查,剔除无效数据、异常数据。故处理后,气象数据剔除蒸发量、大气压力、作物蒸腾蒸发量3个数据项,保留空气温度、空气湿度、风速、风向、光照、雨量、露点温度7个数据项;墒情数据剔除相对含水量的4个数据项,保留体积含水量、土壤温度、土壤盐分的12个数据项。剔除原因均为监测数据不完整,各站点监测项设置有别,只有个别“超级站点”有剔除数据项的监测内容。同时剔除由于设备测试、传感器探头失灵产生的异常数据组。
本研究采用不包含天气预报和包含天气预报2组维度不同的数据分别对2 种模型进行训练模拟。按照模型要求,2 组数据均分为输入数据和输出数据,而2组输出数据均为土壤墒情状况,即体积含水量,包括20、40、60、80 cm 土层的体积含水量。原始数据处理过程:第1 步,增加“站点编号”数据项,因原始数据和预测结果分属各站点,即根据某一站点的数据预测这一站点未来的土壤墒情;第2步,匹配输出数据,模型将预测1 d(24 h)后的土壤墒情,故每组原始数据要匹配24 h 后的墒情数据,比如2020年8月4日10:30的气象墒情原始数据,要匹配2020年8 月5 日10:30 的墒情数据;第3 步,匹配24 h 天气预报数据,对天气预报数据进行数字化处理,然后匹配到相应原始数据中,比如2020 年8 月4 日静海区各站点数据要匹配2020年8月4日的24 h天气预报数据;第4 步,提取测试数据,模拟真实预测场景,从原始数据中随机提取5 000 组数据作为测试数据,剩余10万组数据用于模型训练;最后,将不包含天气预报和包含天气预报2组维度不同的数据分别进行存储。各组数据的输入输出数据项如表2所示。
李桂明还主动交代了几个埋“瓶装”的细节,说药瓶是他妈以前吃药用过的。“我就做了这么点傻事,该咋判咋判吧!”

表2 各组数据的输入、输出数据项
2 模型的建立
2.1 BP神经网络模型
BP 神经网络模型的基本思想是信号的正向传播与误差的反向传播,根据网络输出层实际误差,从输出层开始,反过来调整网络权值,最终使输出的均方误差最小[5]。BP 神经网络的拓扑结构如图1所示。

图1 BP神经网络拓扑结构
2.2 Elman神经网络模型
Elman 神经网络是典型的反馈型神经网络,是一种具有局部记忆单元和局部反馈连接的递归神经网络。它以BP网络为基础结构,在隐含层增加一个承接层,作为一步延时算子,达到记忆目的,从而使系统具有适应时变特性的能力,增强了网络的全局稳定性[6]。Elman神经网络的拓扑结构如图2所示[7]。

图2 Elman神经网络拓扑结构
2.3 传递函数
本研究的BP 神经网络模型的传递函数是Levenberg-Marquardt 算法。Elman 神经网络模型的传递函数采用带动量的梯度下降法。
2.3.1Levenberg-Marquardt 算法 该算法是使用最广泛的非线性最小二乘算法,是利用梯度求最大(小)值的算法,它同时具有梯度法和牛顿法的优点,且算法稳定[8]。当λ很小时,步长等于牛顿法步长;当λ很大时,步长约等于梯度下降法的步长。
2.3.2带动量的梯度下降法 该方法是在反向传播的基础上在每一个权值的变化上附加一项正比于前次权值变化量的值,并根据反向传播法产生新的权值变化。该方法使网络在修正权值时,不仅考虑误差在梯度上的作用,而且还考虑误差曲面变化趋势的影响,从而降低网络对于误差曲面局部细节的敏感性,有效地抑制网络陷入局部极小[9]。
本研究初始计划均采用Levenberg-Marquardt算法,但由于训练数据量大,该算法占用内存高,导致Elman 神经网络模型训练时长增加数倍,故Elman神经网络模型选择带动量的梯度下降法。
3 模型应用评价
本研究模型训练应用的是Matlab 神经网络工具箱,该工具箱默认将10 万组数据按7∶1.5∶1.5 的比例分为训练集、验证集和测试集进行模型训练。各模型的隐藏层节点数量和步长均通过试算确定,经过多次迭代,每次迭代都会按照比例重新分配训练集、验证集和测试集数据,最终使网络训练误差逐步收敛,最后应用5 000 组测试数据模拟真实预测场景。
3.1 不含天气预报的BP神经网络土壤墒情模型
通过对该模型的隐藏层节点和步长的试算,每个节点或步长试算均连续进行15次,最终确定隐藏层节点23个、步长为0.01时,4个土层的平均土壤墒情误差最小,为0.052 075(5.21%),如表3所示。
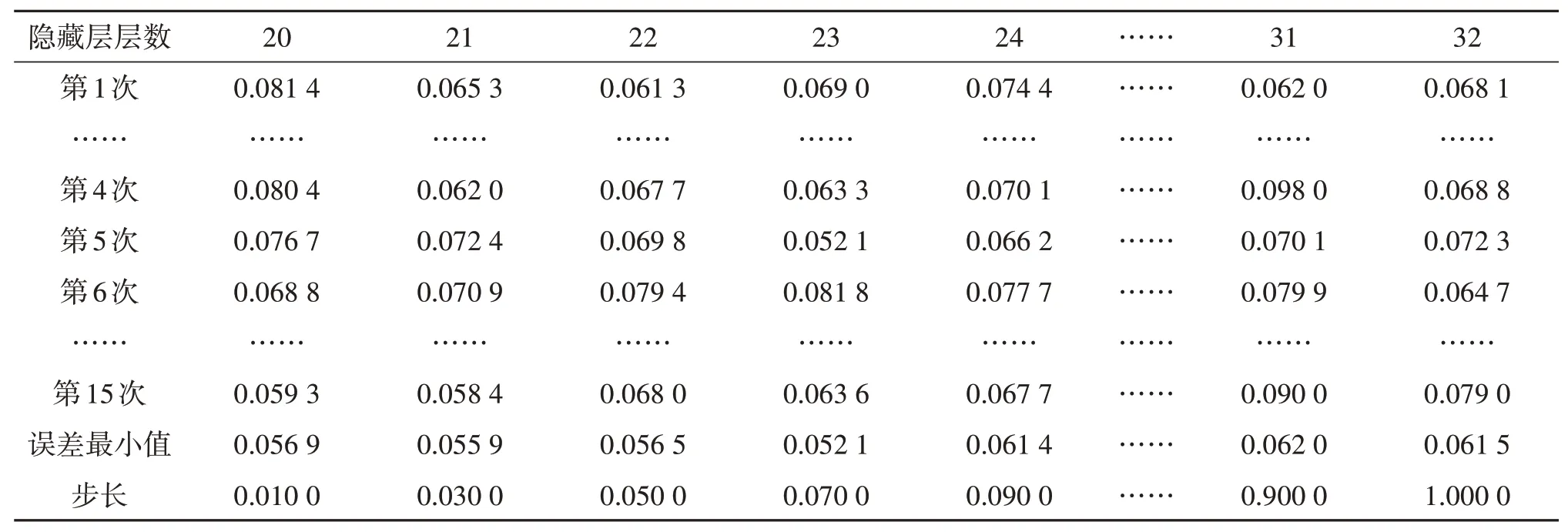
表3 不含天气预报的BP神经网络土壤墒情模型平均误差分析
网络的训练性能和总拟合情况如图3所示。该网络在迭代225次后实现性能最佳,此时网络均方误差为0.004 350 4;网络的总拟合度为0.988 59,回归直线对观测值的拟合程度较好,模型具有良好的准确性和稳定性。模型训练完成后用5 000 组数据进行测试,测试结果误差曲线如图4所示。
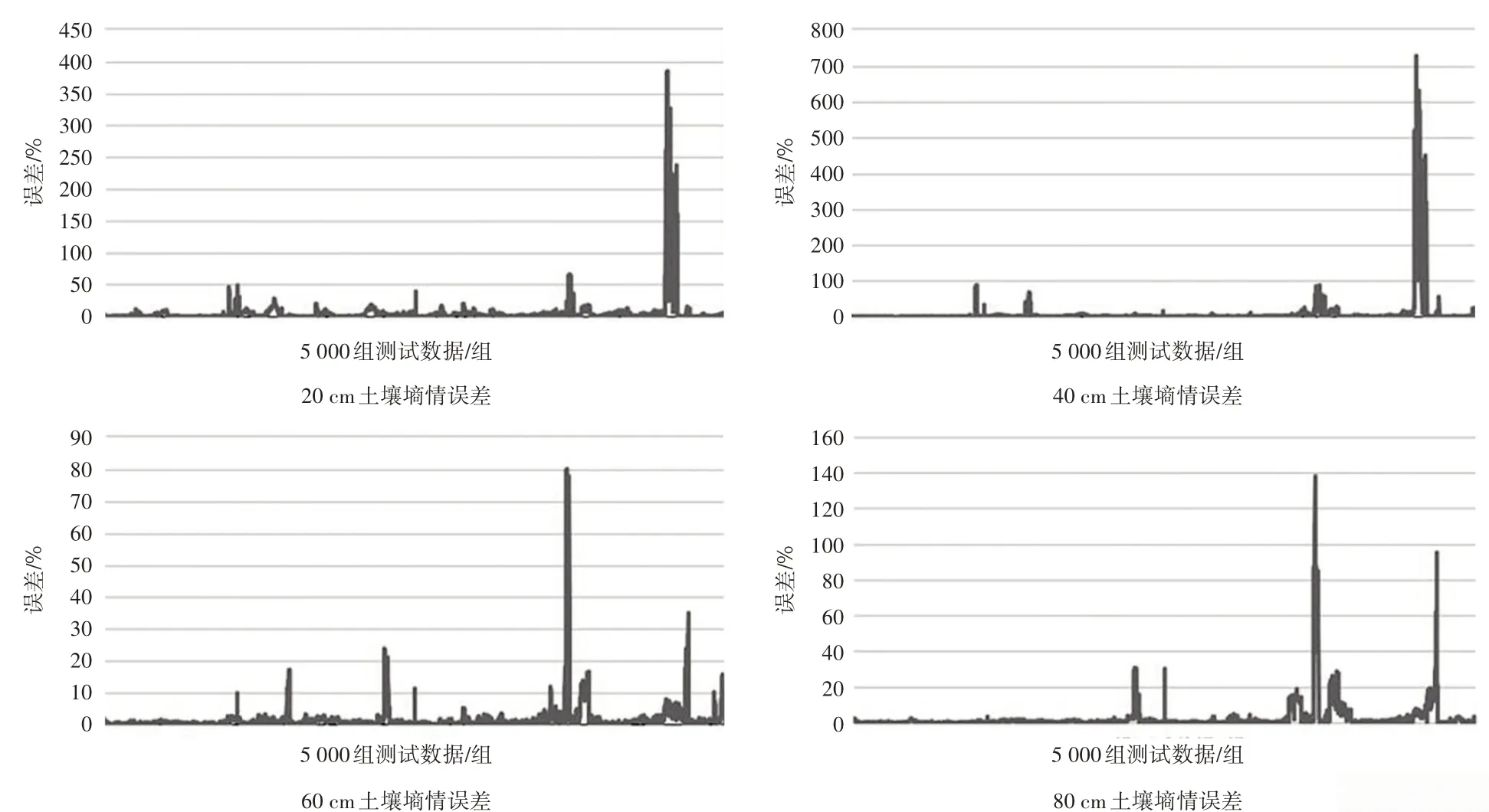
图4 不含天气预报的BP神经网络模型测试数据误差
从误差曲线看出,该模型测试数据的误差比较平稳,整体波动较小,其中20、40 cm 土层墒情预测误差最大达到近400%、750%,60、80 cm 土层墒情预测误差最大达到80%、140%。
3.2 含天气预报的BP神经网络土壤墒情模型
通过对该模型隐藏层节点和步长的试算,每个节点或步长试算均连续进行15次,最终确定隐藏层节点39个、步长为0.01时,4个土层的平均土壤墒情误差最小,为0.044 55(4.46%),如表4所示。

表4 含天气预报的BP神经网络土壤墒情模型平均误差分析
网络的训练性能和总拟合情况如图5所示。该网络在迭代131 次后实现性能最佳,此时网络均方误差为0.002 661 1;网络的总拟合度为0.992 83,回归直线对观测值的拟合程度较好,模型具有良好的准确性和稳定性。模型训练完成后用5 000 组数据进行测试,测试结果误差曲线如图6所示。
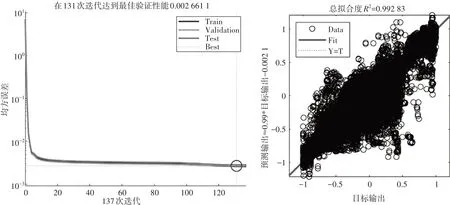
图5 含天气预报的BP神经网络土壤墒情模型训练性能和总拟合情况
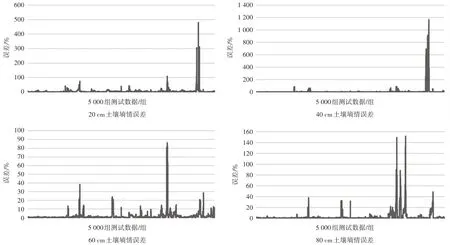
图6 含天气预报的BP神经网络土壤墒情模型测试数据误差
从误差曲线看出,该模型测试数据的误差比较平稳,整体波动较小,其中20、40 cm 土层墒情预测误差最大达到近500%、1 200%。60 cm 土层墒情预测误差波动较其他3个土层更多,但幅度较小,最大误差不及90%。
3.3 不含天气预报的Elman神经网络土壤墒情模型
通过对该模型隐藏层节点和步长的试算,每个节点或步长试算均连续进行15次,最终确定隐藏层节点25 个、步长为0.3 时,4 个土层的平均土壤墒情误差最小,为0.031 45(3.15%),如表5所示。
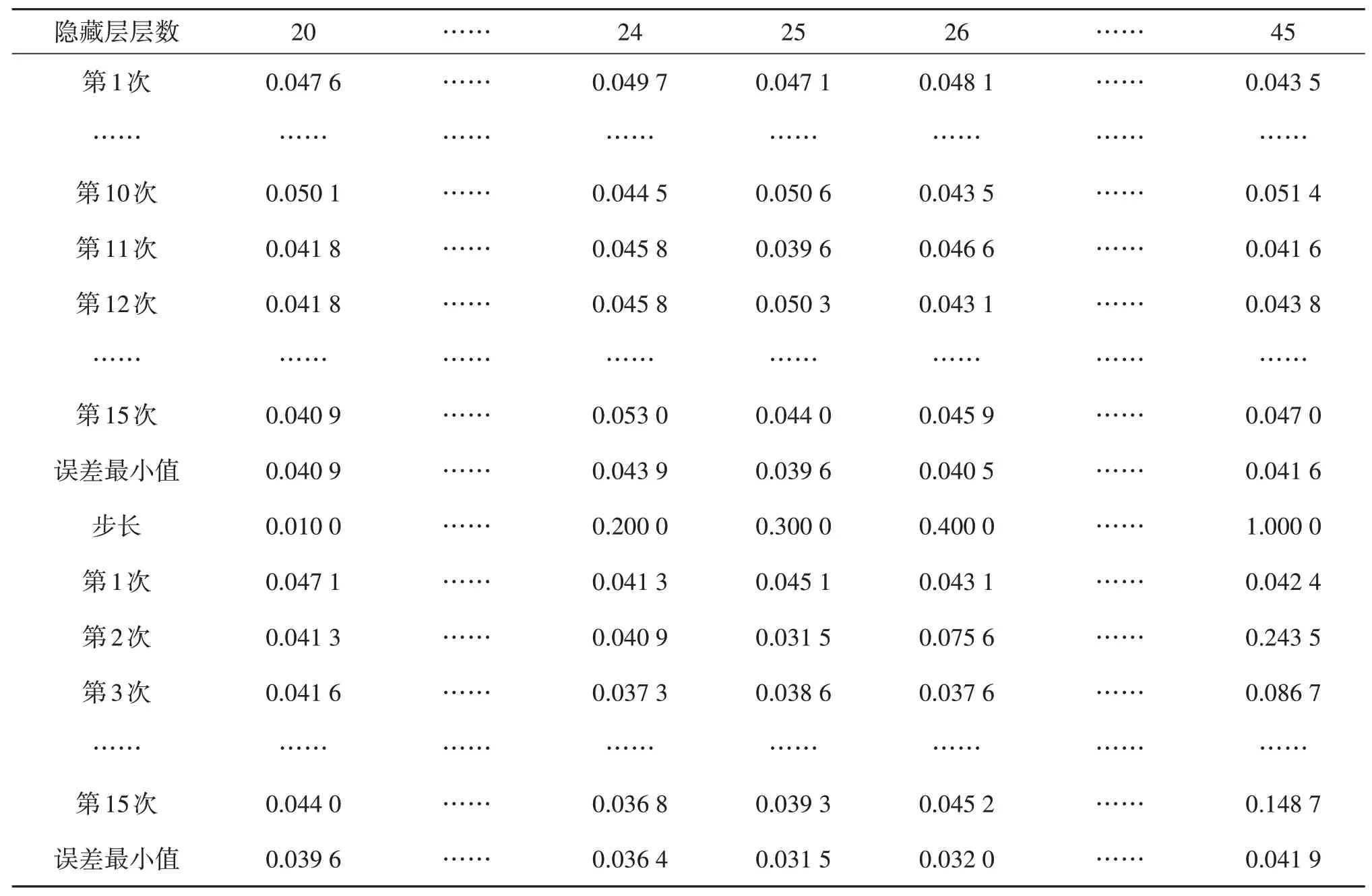
表5 不含天气预报的Elman神经网络土壤墒情模型平均误差分析
网络的训练性能如图7 所示,经过50 000 次迭代训练该网络的均方误差为0.005 280 2,已达到最佳训练性能。模型训练完成后用5 000 组数据进行测试,测试结果误差曲线如图8所示。

图7 不含天气预报的Elman神经网络土壤墒情模型训练性能
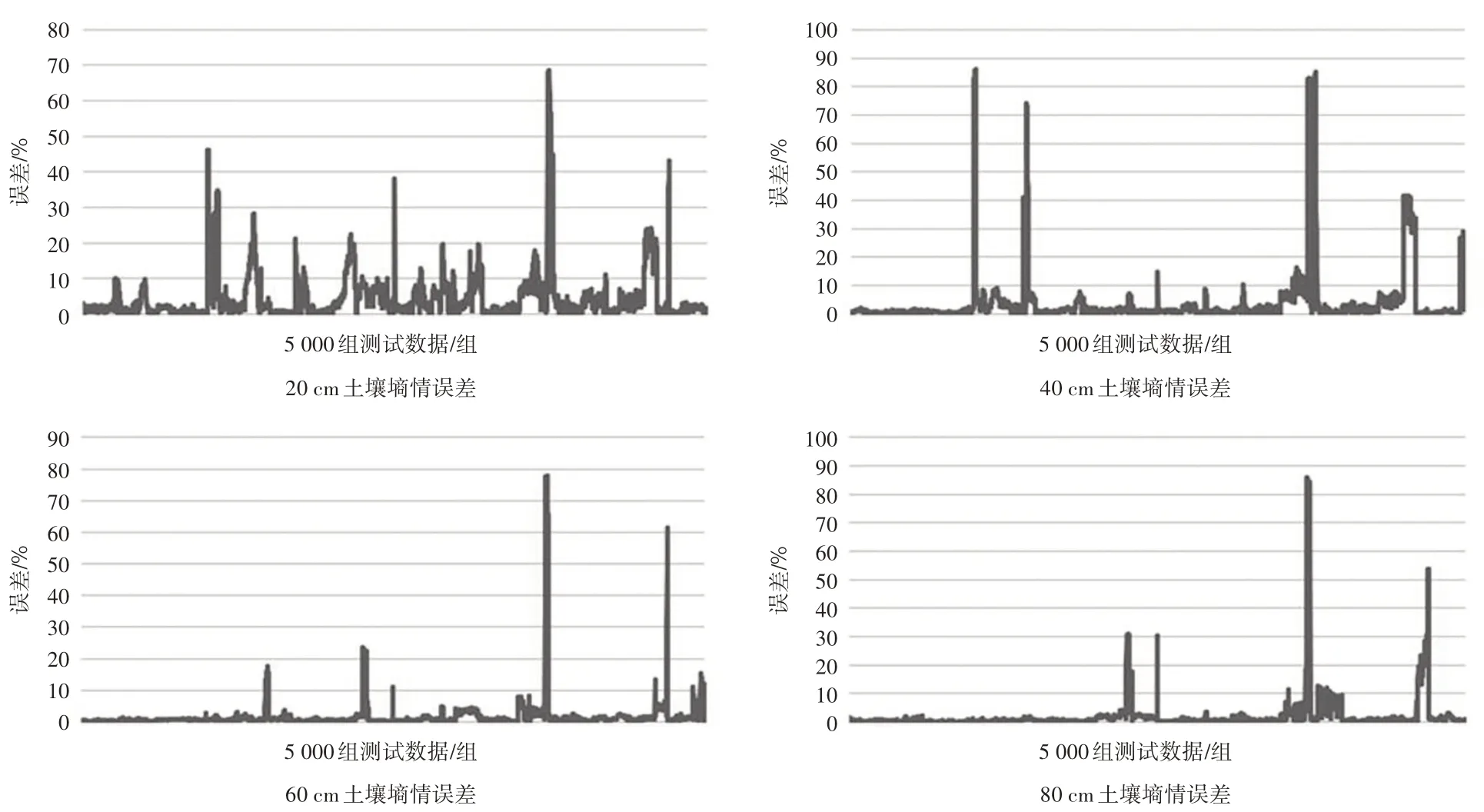
图8 不含天气预报的Elman神经网络土壤墒情模型测试数据误差
从误差曲线看出,该模型测试数据的误差整体波动较小,误差最大值较BP 神经网络模型小很多,其中20、40 cm 土层墒情预测误差最大值不到70%、90%,60、80 cm墒情预测误差最大值不到80%、90%。
3.4 含天气预报的Elman神经网络土壤墒情模型
通过对该模型隐藏层节点和步长的试算,每个节点或步长试算均连续进行15次,最终确定隐藏层节点38 个、步长为0.5 时,4 个土层的平均土壤墒情误差最小,为0.033 575(3.36%),如表6所示。
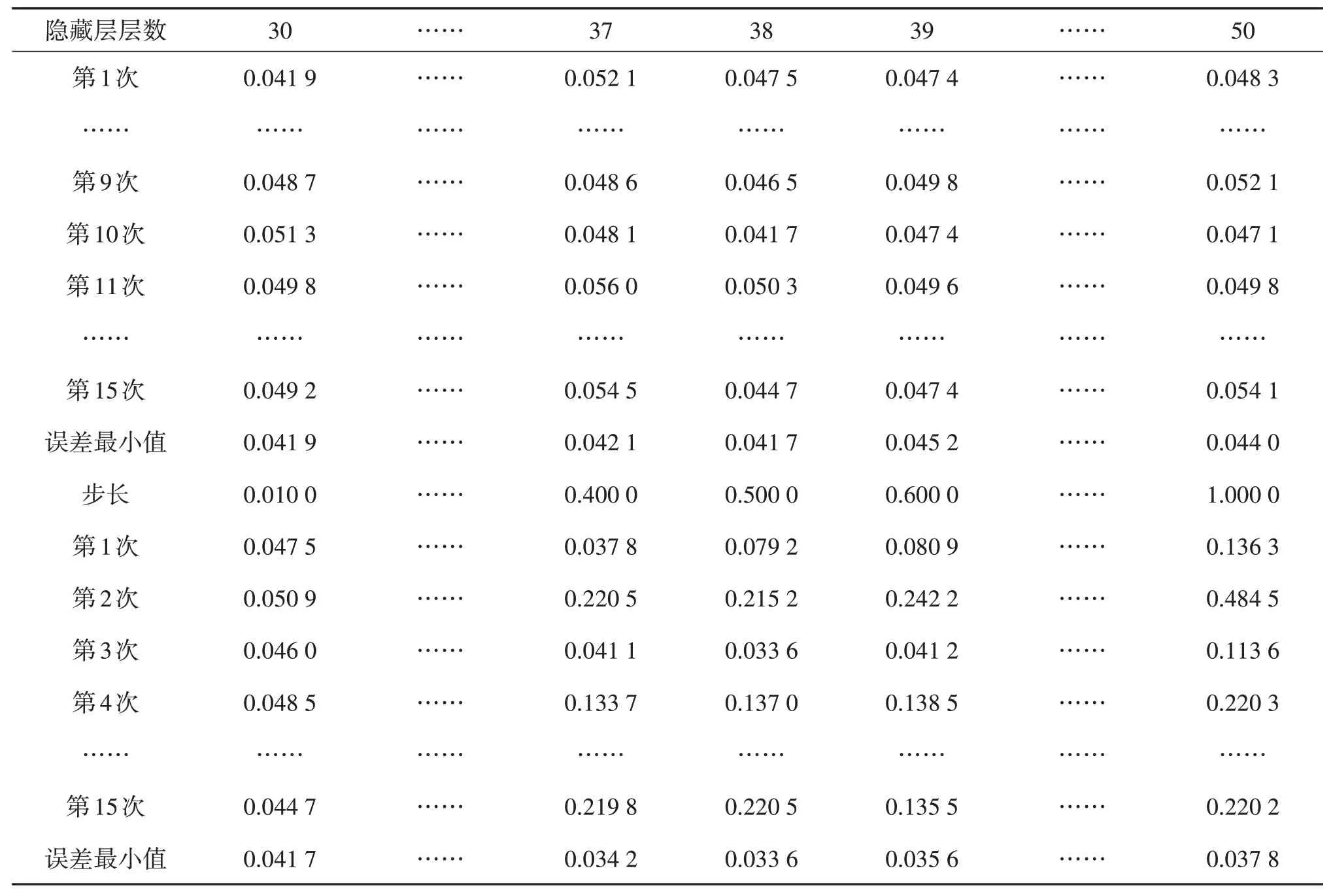
表6 含天气预报的Elman神经网络土壤墒情模型平均误差分析
网络的训练性能如图9 所示,经过50 000 次训练该网络的传递误差大小为0.005 090 1,已达到最佳训练性能。模型训练完成后用5 000 组数据进行测试,测试结果误差曲线如图10所示。
图10 含天气预报的Elman神经网络土壤墒情模型测试数据误差
从误差曲线看出,该模型测试数据的误差整体波动情况与不含天气预报的Elman神经网络模型相似,各土层误差最大值与不含天气预报的Elman 神经网络模型一致,较BP神经网络模型小很多。
3.5 各模型训练过程综合分析
BP、Elman 神经网络预测模型各土层墒情误差及方差结果见表7。
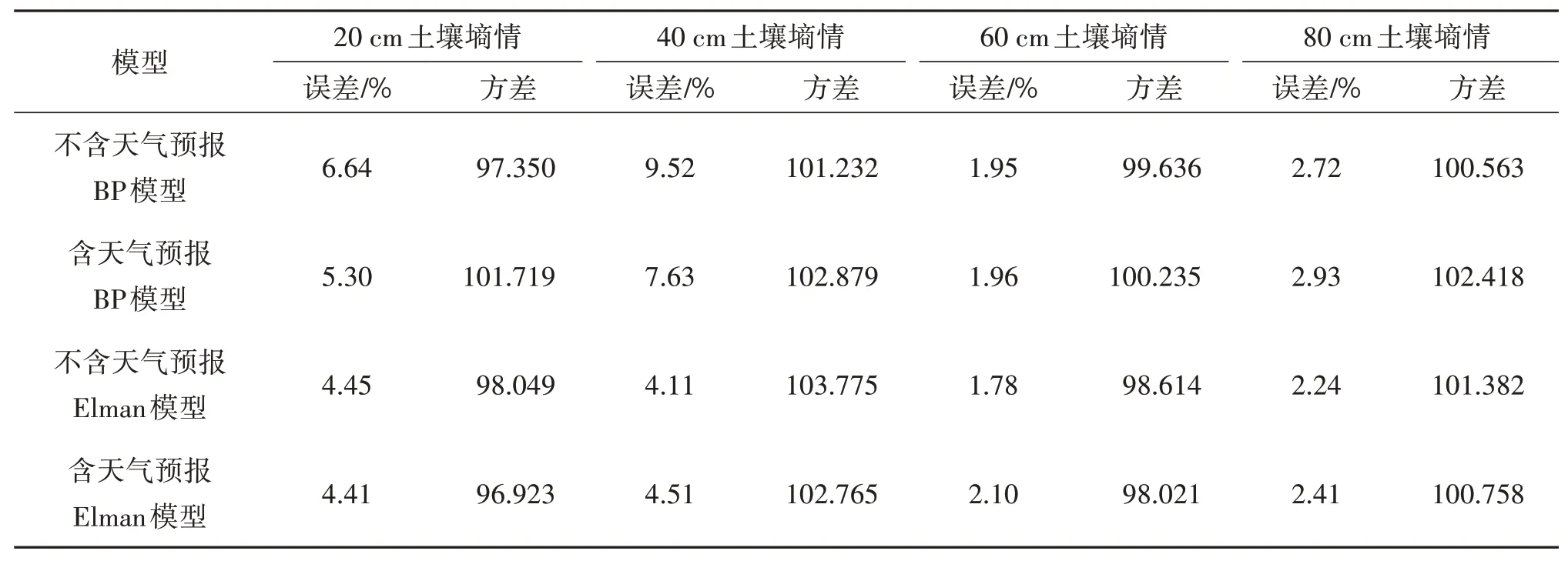
表7 各模型各土层墒情误差和方差结果
4 讨论与结论
本研究建立BP、Elman 神经网络预测模型,采用2 组维度不同的数据分别对这2 种模型进行训练模拟,预测1 d(24 h)后的土壤墒情,通过对5 000 组测试数据结果及各模型训练过程进行综合分析,得出以下结论。
1)从总体看,Elman 神经网络模型的精度比BP神经网络模型的更高,输入的数据不论是含天气预报还是不含,精度都高于BP神经网络模型。这是因为Elman 神经网络是一个反馈型网络,通过承接层记忆隐含层单元前一时刻的输出值达到反馈目的;而BP 神经网络则没有反馈。由于Elman 神经网络增加了反馈,所以其训练时间长于BP 神经网络,在本研究中,Elman 神经网络的训练时间是BP 神经网络的2~3倍。
2)土壤墒情与天气状况密切相关,所以从理论上讲,含天气预报的模型精度比不含天气预报的模型精度高。但实际发现,BP神经网络模型基本表现出这一相关性;而Elman 神经网络模型并没有表现出这一相关性,含天气预报模型的误差略高于不含天气预报模型的误差,而其方差在4 个土层上都小于后者,这可能是天气预报数据精度及农田灌溉操作的影响,因为本研究的天气预报数据是区县级数据而非站点区域性数据,而且对各站点的农田灌溉未作考虑和统计。
3)4个土层的土壤墒情误差差别较大,20、40 cm土层的墒情误差明显高于60、80 cm 土层。从模型测试数据误差图中也能看出20、40 cm 土层墒情的波动比60、80 cm土层的波动大。这是因为20、40 cm土层墒情受天气等外界的影响较大,水分要渗入60、80 cm 土层需要较大的雨量,而天津地区较大雨量只集中在每年7、8 月份的某几天,所以60、80 cm土层墒情误差的波动较小。
本研究预测1 d(24 h)后的土壤墒情,预测误差控制在5%以内,说明该模型是可用的。但在实际中,预测获取1 d 后的土壤墒情,对农业生产的作用和意义不是很大。农作物生长是一个长期过程,土壤墒情的短期或超短期的微小变化对农作物生长的影响不大,所以在农业生产过程中,中长期(5、10、15、30 d)的土壤墒情预测意义深远。本研究团队将继续应用Elman神经网络或其他神经网络研究中长期预测模型,以最终实现指导农业生产、提高农作物产量的目的。

