基于深度强化学习的掼蛋扑克博弈求解
葛振兴 向 帅 田品卓 高 阳,3
1 (计算机软件新技术国家重点实验室(南京大学) 南京 210023)
2 (上海大学计算机工程与科学学院 上海 200444)
3 (南京大学深圳研究院 广东深圳 518057)
(zhenxingge@smail.nju.edu.cn)
游戏博弈作为现实世界的一种高度抽象,具有良定义、易检验算法性能等特点,成为目前智能决策研究的热点. 近些年,一系列人工智能方法在游戏中均取得了很好的效果,甚至战胜人类,彰显出人工智能在现实应用中极大的潜力,具有重大的意义. 而且,不断有新的算法在各类游戏博弈中取得重要进展. 如在围棋中,以AlphaGo[1]和AlphaZero[2]为代表的人工智能战胜了李世石、柯洁等人类顶尖高手;Libratus[3]和Pluribus[4]战胜德州扑克(Texas Hold’em)职业冠军;Suphx[5]在天凤麻将平台超越职业选手段位;AlphaStar[6],OpenAI-Five[7]分别在星际争霸中与DOTA2 中战胜人类世界冠军等.
目前针对棋牌类游戏存在多种求解方式,例如:1)基于强化学习(reinforcement learning)的方法[1-2,6-8]采用试错的方式学习智能体在自身观测状态下的最优策略,通过深度神经网络拟合状态动作值函数或状态动作概率分布的方法,根据获取到的经验更新相应神经网络,得到更好的策略;2)基于反事实遗憾最小化(counterfactual regret minimization,CFR)的方法[3-4,9-10]采用类似在线学习的方式,在每一轮迭代中计算每种自身观测状态下所有动作的反事实遗憾,根据遗憾匹配(regret matching)等遗憾最小化方法生成新一轮策略,尝试降低新策略的遗憾,最终输出每一轮的平均策略;3)通过在线优化的方法,如一阶方法(first order method)[11],将中小规模二人零和博弈问题建模为一个凸优化问题进行求解.
国内扑克游戏,如掼蛋、斗地主等,作为一类非完美信息博弈,相较于目前已有较好算法的德州扑克等游戏博弈有较大差异. 国内扑克游戏具有信息集状态多、动作空间复杂、状态动作难以约简等特点[8],因此大部分现有方法难以应用. 例如用于求解德州扑克的蒙特卡洛反事实遗憾最小化[10,12](Monte Carlo counterfactual regret minimization,MCCFR)算法虽然能缓解在求解德州扑克问题时由于博弈树大小而引发的难以迭代遍历问题[13],但是斗地主或掼蛋这样无法简单进行状态动作空间约简的扑克游戏,其博弈树规模仍过于庞大,无法简单适用;经典的强化学习方法如DQN[14-15],A3C[16-17]等则由于较大的动作空间导致这些算法的网络结构难以较好地拟合扑克类的值函数[8],从而无法在掼蛋、斗地主等国内扑克类游戏中取得较好的效果.
深度蒙特卡洛[8](deep Monte Carlo,DMC)方法是目前针对国内扑克游戏设计人工智能算法所面临问题的主要解决途径之一. DMC 方法采用蒙特卡洛采样评估状态动作值函数,其考虑到斗地主等扑克游戏动作不易约简且动作之间由于出牌相似而具有相似关系的特点,通过将动作进行编码与状态一同作为神经网络的输入,借此解决动作空间大且不易约简的问题. 同时DMC 方法采用TorchBeast[18]训练框架,通过大量采样来降低训练方差,在斗地主游戏中取得了较好的效果. 但是单纯的DMC 方法在面对以掼蛋为代表的更大规模扑克博弈时,依然面临一些问题:1)DMC 方法需要大量的训练时间. 采用DMC方法的DouZero 系统,在对抗专家策略的监督学习方法时,在斗地主环境中需要10 天时间才能达到50%的对抗胜率. 因此对于更复杂的扑克博弈如掼蛋,其信息集数量、信息集大小、动作空间、每局历史信息长度均远超斗地主,需要更多的训练时间. 2)DMC 方法实际执行策略过程中总是选择第1 个状态动作值最大的动作,因此在实际对局过程中更容易被对手利用. 同时由于DMC 训练过程中的高方差原因,较小的值扰动也可能造成较大的策略差异,从而造成策略质量较大的变化.
为了有效解决训练时间问题,考虑到在常见的扑克博弈中,存在大量的已有知识或领域知识,因此如果能够将现有的先验知识融入算法的训练过程,将大大提升算法的训练效率. 为此文献[19]提出一种暖启动(warm start)方法,该方法针对反事实遗憾最小化算法进行暖启动,通过已有策略,赋予在每个信息集中的动作一个合适的反事实遗憾值,从而实现对于策略求解的加速计算. 然而,暖启动方法需要获取整个博弈信息,从而进行期望值与遗憾值的计算,因此对于大规模扑克博弈需要进行大幅度的状态与动作的约简,而这对于斗地主、掼蛋等国内主流扑克博弈难以实现,相关方法较难直接应用.
因此本文提出了一种软深度蒙特卡洛(soft deep Monte Carlo,SDMC)方法,对以掼蛋为代表的国内扑克类博弈进行求解. 首先针对DMC 方法需要大量训练时间的问题,提出通过软启动(soft warm start)方式,结合已有策略知识,在训练过程中进行已有策略决策与SDMC 策略模型决策的混合决策,辅助进行策略训练,提升策略收敛速度;然后在实际对战过程中依据策略模型状态动作值预测,通过软动作采样(soft action sample,SAS),缓解DMC 方法仅选择最大值动作时,由于策略固定而易被对手利用等问题,增强策略鲁棒性. 最后,本文在掼蛋博弈中进行实验验证. 本文提出的SDMC 方法在第2 届“中国人工智能博弈算法大赛”取得冠军,在与DMC 方法和第1 届冠军等其他参赛算法进行对比实验证明了本文所提出的方法在掼蛋扑克博弈中的有效性.
1 相关背景
1.1 掼蛋扑克的博弈问题建模
掼蛋扑克博弈问题由于具有无法观测对手手牌内容、独立决策的特性,经常被建模为一个部分可观测的马尔可夫决策过程(partially observable Markov decision process,POMDP). 在部分可观测马尔可夫决策过程中,智能体i表示智能体的编号索引,状态s表示当前实际状态. 在每一个时间点t,每一个智能体i都会观测到一个观测状态oi=Z(S,i),这里函数Z是一个观测函数. 在每次智能体观测到观测状态oi时,智能体i都可以选择一个动作a. 因此,智能体i的策略 πi可以看做一个动作观测历史(action-observation history,AOH)的函数. 每当所有智能体执行一个动作后,当前状态st会根据环境转移函数转换到新的状态st+1~P(st+1|st,a),其中a=(a0,a1,…)为所有智能体的联合动作,每个智能体i会收到环境的奖励=Ri(st,a). 因此当前状态下的轨迹可用τt={s0,a0,s1,a1,…,st-1,at-1,st}表示. 在POMDP中,智能体i目标在于最大化自身奖励Jπ=Eτ~P(τ|π)[R(τ)],其中函数为智能体收到的折扣累计奖赏, γ为累计折扣因子.
掼蛋扑克博弈,具有序贯决策特性,即每个AOH 下最多有1 个智能体进行决策,状态转移函数可约简为其中ai为当前智能体决策. 由于扑克博弈的关键信息通常由2 部分组成:手牌、已打出牌等当前状态信息与所有参与博弈的智能体的历史动作信息,且可以通过当前观测状态与历史动作信息对牌局进行复盘,故掼蛋博弈的AOH可由=〈Z(st,i),Ht〉进行表示,其中∈Ht为智能体i在包含时刻t前的动作历史掼蛋扑克博弈不同于普通的POMDP,其奖励值往往仅存在于终止状态集合Sterminal,因此对于非终止状态st,所有智能体获取到的奖励为0,即因此累计折扣因子通常可以设置为1.
1.2 相关研究进展
本节首先介绍现有扑克类博弈的求解方法,并分析各个方法的优缺点;其次着重介绍在斗地主中的最新方法,从而更好地介绍本文提出的SDMC方法.
1.2.1 扑克类游戏求解方法
扑克类游戏作为一种天然的非完美信息博弈,已经具有悠久的研究历史.
针对竞争型的扑克类游戏,如德州扑克,通常采取求解纳什均衡的方式. 其中为代表的CFR[9]采用自博弈的方式进行训练. 在训练的每一轮中,个体与上一轮训练出的策略进行对抗,并依靠遍历整棵博弈树的方式计算策略的遗憾,通过最小化遗憾的方式最终求解博弈的纳什均衡. 但受制于CFR 的遍历过程,随着博弈规模的增加,遍历整棵博弈树需要极大的时间与空间,因此MCCFR[10]方法采取采样的方式更新博弈策略的遗憾,降低算法需求. 虽然CFR 类的方法在以德州扑克为代表的博弈中取得惊人的效果,但是其方法限制了其在大规模环境下的应用,往往需要结合博弈约简(abstraction)[20]方法,降低博弈树规模. 因此难以处理如掼蛋、斗地主等非完美信息博弈.
而对合作型的扑克类游戏如Hanabi,则有着更为多样的求解范式. 不同于竞争型博弈下致力于求解纳什均衡而将其看作一个优化问题,合作型博弈也可以建模为一类学习问题[21]. 其中贝叶斯动作编码器(Bayesian action decoder,BAD)[22-23]方法在Hanabi 中取得了最为理想的成果. BAD 方法使用深度强化学习的方式在公共信念中探索合适的策略,但此类方法仅面向纯合作类场景选取确定性动作,无法简单适用到如掼蛋这样具有竞争合作的混合场景中.
针对掼蛋、斗地主等牌类博弈面对状态、动作空间复杂不易求解等问题,You 等人[24]提出通过一种组合Q 网络(combinatorial Q-network)的方式,将决策过程分为组牌和出牌2 个步骤. 但组牌过程耗时巨大,不利于在大规模环境下的训练.DeltaDou 方法[25]通过贝叶斯推断的方式推理对手的卡牌,之后采用类似于AlphaZero 的方式进行蒙特卡洛树搜索,从而对策略进行训练,但仍需约20 天的训练时间才能在斗地主中达到专家水平.
1.2.2 深度蒙特卡洛方法
DMC 方法是由Zha 等人[8]提出,是应用在斗地主环境下DouZero AI 系统中的核心算法. DMC 方法考虑到斗地主等扑克游戏动作不易约简且动作之间存在相似关系的特点,通过将动作进行编码与状态一同作为神经网络的输入,解决现有其他方法在大规模具有相似动作的空间下不适用的问题. 具体来讲,DMC 方法尝试训练神经网络V,使其输出值与实际的值函数尽可能地相近:
其中 θ为神经网络V的参数,且
在训练过程中,DMC 方法采用 ∊-贪心的策略选择方法,即给定神经网络和参数Vθ,训练过程中选择的策略
其中 |A|为当前可选动作数量,为指示函数(indicating function)且仅在参数为真时结果为1,否则为0,arg max函数选择值最大的第1 个动作.
在实际博弈过程中,DMC 方法直接选择值函数最大的动作,即在AOH 选择,可选动作集合A下,策略为
2 软深度蒙特卡洛方法
本节将介绍SDMC 方法,SDMC 方法包含软启动与软动作采样2 个过程,解决现有方法在以掼蛋为例的扑克博弈中的问题. 同时,为了更好地进行深度学习训练,本文亦创新性地提出了一种针对深度学习的掼蛋扑克博弈编码方法.
2.1 软启动蒙特卡洛方法
DMC 方法将动作观测历史与可选择动作进行结合,作为神经网络输入,通过蒙特卡洛采样方式对值函数进行拟合,采样策略根据神经网络预测值采用 ∊-贪心的策略.
由于DMC 方法采用随机网络进行初始化,再通过自博弈的方式不断自我对战产生样本,并进行更新. 因此在训练初期DMC 自博弈产生的博弈轨迹样本的值更多是面对对手使用随机策略时的动作值,由此产生出的策略往往并不具有实用价值,只是训练迭代过程中的中间策略,为后续更强策略的训练提供基础.
为了加快策略的训练过程并尽量降低因加速训练过程而产生的影响,本文提出了软启动DMC 方法,通过软启动的方式进行训练,借助已有策略,尽量加速训练过程.
具体的,对于已有策略 πE,软启动DMC 尝试融合借鉴预训练方法. 常见的预训练通过训练一个神经网络模型Vθ,使得其输出预测值与已有策略值函数尽可能相近,即
但是已有策略的值函数由于掼蛋扑克博弈规模过大通常难以直接获取,因此可以通过蒙特卡洛采样的方式进行自博弈模拟评估:
但由于已有策略具有先验知识,有较多的动作并不会主动选择,故直接自博弈评估时可能存在较多的动作没有给出评估值,从而出现如过估计[26]等问题. 而通过在已有策略 πE中加入 ∊-贪心的方式可以部分缓解该问题,但仍面临若 ∊设置较大,则自博弈的评估并非已有策略值;而若 ∊设置较小,则由于探索样本比例较低,需要大量的训练才可进行较好的拟合,出现与最初降低训练时间需求的初衷相违背的问题.
考虑到由于已有策略并非一定最优,经过初始化过后仍需采取自博弈的方式进行训练,因此软启动考虑在训练过程中融入已有策略而非如文献[19]直接去拟合已有策略方式,如图1(a)所示. 这样既融入了已有策略对当前模型训练进行加速,同时又避免了普通的暖启动方法所面临的过估计等问题.
具体来讲,软启动结合已有策略与当前模型生成策略的自博弈评估值代替式(5)中的已有策略评估值即
为混合了2 种决策模型的 ∊-贪心策略,其中权重 ω为软启动参数,可随着训练的进行而衰减.
具体算法流程如算法1 所示.
算法1.软启动蒙特卡洛.
为空,其中n为智能体数量;随机初始化SDMC
① forepisode=1 tomax_episodes
② fort=0toT
③i←当前行动智能体编号;
④ 智能体i观测到动作观测历史;
⑧ end for
⑨ 获得环境奖励r=(r1,r2,...,rn);
⑩ fori=1ton
⑪ for 至经验缓存Di;
⑫ 存储样本
⑬ end for
⑭ 清空经验缓存Bi;
⑮ whileDi.length>batch_size
⑯ 从Di采样并更新神经网络Vi;
⑰ end while
⑱ end for
⑲ end for
对于掼蛋这类大规模扑克博弈,可以通过TorchBeast[18]框架进行并行训练. 具体对于算法1来说,每一个actor 执行算法1 中 ①~⑭步,并在每次循环开始之前与learner 同步模型;learner 执行⑮~⑰步.
2.2 软动作采样
传统DMC 方法在使用模型决策时,一般选择最大值的动作,即对于动作观测历史和可选动作集合A,由式(4)选择动作. 但由于仅选择最大值的动作容易受到微小扰动的干扰,如训练方差等,导致策略大幅度变化,因此评估值较为接近的动作都有可能是最好的动作,且在实际使用过程中完全确定性的策略较易被对手猜测出自身手牌等信息,因此采用带有软动作采样(soft action sample,SAS)的动作选择方式,流程如图1(b)所示,在保证所选动作在当前模型的评估下评估值变化不大的前提下,通过舍弃可选动作集合中值较低的动作,保留评估值与最大值接近的备选动作,构造备选动作集合,并在备选动作集合中对每一个动作的值进行softmax 处理,按比例分配被选择的概率:
对于阈值的选择需要保证其与最大值尽量接近,可根据当前所有动作的值的分布选择. 具体而言,可以通过设置较小的阈值权重 ω′选择vτti:
原则上,阈值的选择应保证将所有最优动作筛选出来,并摒弃所有非最优动作. 若能精确估计所有动作的Q值,则权重 ω′应设为0,即仅选择最优的动作. 但由于训练过程中的采样带来的方差扰动,使得最优动作的Q值并非准确值,故而需采用较小的权重. 随着训练过程的增加,Q值愈发准确,可适当降低权重大小.
软动作采样算法流程如算法2 所示.
算法2.软动作采样.
输入:决策模型Vθ,动作观测历史,可选动作集合A,阈值权重 ω′;
输出:模型最终选择动作ai.
① 由式(11)计算阈值v;
③P←(0,0,...,0); /*初始化每个动作的概率为0*/
④ fora′in
⑤ 由式(9)计算每个动作的概率P(a′);
⑥ end for
⑦ai~P; /*根据概率分布P采样一个动作ai*/
⑧ 返回结果ai.
2.3 掼蛋扑克博弈编码框架
对状态信息进行编码是深度强化学习在扑克环境中进行应用的重要组成部分,本节从DouZero[8]针对斗地主的编码方法出发,根据掼蛋扑克游戏与斗地主的不同,创新性地提出一种适用于掼蛋扑克游戏的编码框架.
对于掼蛋扑克牌局状态的编码应至少包含3 部分:私有信息、当前可出牌与公共信息. 私有信息一般则为自己的手牌;当前可出牌包含所有可能出牌动作;公共信息包含出牌记录与对局信息,牌局信息指如掼蛋中的牌局等级信息、当前其余玩家手牌数量等当前对局的信息. 在此基础上可以添加额外的信息辅助深度网络进行训练.
状态的编码均采用1 位有效编码的形式. 手牌信息根据游戏使用的牌数量构建不同大小的空矩阵,若使用n副牌则构建n×(4×13+2)大小的矩阵,其中4×13+2表示1 副牌,4 为花色索引,13 为点数索引,2 表示大小王,当拥有某张手牌时,对应位置的矩阵数值置为1. 对于标准掼蛋规则,由于使用2 副牌,因此n=2,具体卡牌编码如图2“卡牌表示”部分所示.
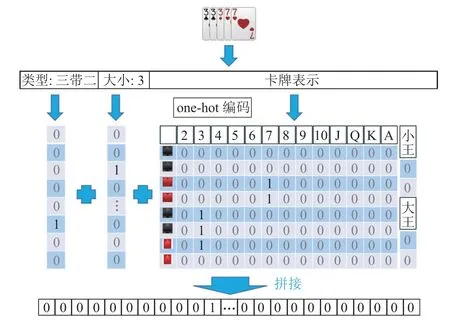
Fig.2 An example of information encoding in GuanDan poker game图2 掼蛋扑克信息编码示例
出牌动作的编码类似手牌编码方式,分别对出牌动作的类型、大小与所使用的牌进行编码. 对类型、大小的编码可解决相同出牌具有不同出牌类型与大小情况,如掼蛋中部分具有逢人配的顺子等,以及区分在编码出牌记录时无出牌记录的0 填充编码与“过牌”(PASS)在编码时的区别,并提供额外的信息辅助神经网络处理,如图2 所示.
对于出牌记录的处理主要包括对出牌动作的编码与出牌动作结构的组织. 对于SDMC 与DMC 等方法,出牌记录信息会被输入到循环神经网络,因此可采取序列式结构对出牌进行组织,即从下家出牌到智能体自己出牌为止1 轮的出牌编码进行拼接.
3 实验与结果分析
本节对本文提出的SDMC 方法进行实验分析,使用掼蛋扑克环境,衡量SDMC 方法中软启动的加速训练效果,并分别与第1 届、第2 届“中国人工智能博弈算法大赛”的参赛算法对比,证明SDMC 方法的有效性.
3.1 掼蛋扑克介绍
掼蛋是国内一种广泛流传的扑克类博弈. 掼蛋博弈使用2 副扑克牌,共108 张牌,采取2 对2 的模式对抗,其中每个博弈玩家与对家为1 支队伍进行对抗. 本文采用第2 届“中国人工智能博弈算法大赛”中的掼蛋规则,下面简要介绍.
1) 等级. 1 局掼蛋博弈可以分为若干小局,每小局根据双方队伍等级中最高的决定当前牌局等级,并依据小局胜负情况更新双方的等级. 掼蛋对局中初始双方等级为2,之后依次为3,4,5,6,7,8,9,10,J,Q,K,A.
2) 升级. 每小局对战结束后,仅第1 个出完牌的玩家(称为上游)所在队伍可以升级,升级数依据队友出完牌的顺序决定:若队友第2 个出完牌(称为二游),则升3 级;第3 个出完牌(称为三游),则升2 级;若队友最后1 个出完牌(称为下游),则只升1 级.
3) 获胜条件. 当一方队伍到达等级A,并且队伍中一人获得上游,另一人获得二游或者三游.
4) 特殊牌. 掼蛋中和当前牌局等级相同的牌为级牌,其中红桃级牌称为逢人配,可当作任意牌与其他花色牌组合使用.
5) 牌型. 掼蛋中牌型如下:单张、对子、三连对、三同张、二连三、三带二、顺子、同花顺、炸弹、天王炸. 其中炸弹张数多者为大,同样张数按照点数排序,同花顺大于任意不超过5 张的炸弹,天王炸为2 张大王和2 张小王为最大牌型.
6) 牌点大小. 掼蛋中牌点从大到小依次为:大王、小王、级牌、A、K、Q、J、10、9、8、7、6、5、4、3、2.A 在搭配成三连对、二连三、顺子、同花顺时,可视作1.
7) 进贡、还贡. 从第2 小局开始,由上一轮的下游向上游进贡,挑选1 张除红心级牌之外最大的牌给上游. 上游选择1 张不大于10 的牌给下游还贡. 如果上一局出现一方队伍获得三游和下游,则队伍2人均向对方队伍分别进贡和接受还贡. 如进贡方有2个大王,则可以不进贡.
掼蛋由于使用2 副牌,因此具有更高的求解复杂度,对算法训练效率提出了更大挑战. 仅第1 轮发牌后的信息集的数量级约为1020,远超斗地主等扑克博弈(斗地主的第1 轮发牌后数量级约1014,如考虑去除斗地主的花色影响约为108). 同时考虑到各个玩家拥有更多的手牌产生的指数级增长的可选动作以及等级、逢人配等因素,掼蛋实际信息集数量与大小远超斗地主等扑克博弈.
3.2 实现细节
本节主要描述了基于SDMC 的掼蛋智能体实现细节,包含整体架构、状态编码方式与奖励设计3 个方面.
1) 整体架构细节
基于SDMC 的掼蛋智能体主要由2 部分组成:掼蛋贡、还牌规则决策模块与出牌的SDMC 决策模块. 其中所使用的掼蛋贡、还牌规则决策模块采用第1 届“中国人工智能博弈算法大赛”的冠军规则. 出牌的SDMC 决策模块中,式(11)中
SDMC 的网络结构与文献[8]相似,均采用LSTM网络处理历史动作,通过6 层全连接网络输出动作评估值.
2) 状态编码方式
掼蛋编码方式采用2.3 节编码框架,每一部分的编码大小如表1 所示.

Table 1 State Representation of GuanDan Games表1 掼蛋环境状态编码
3) 奖励设计
如3.1 节介绍的,掼蛋胜负取决于队伍积分是否超过A,因此通过判断大局胜利的方式给予2 队智能体奖励,可能会导致较差的小局内策略获得正奖励,因此在掼蛋环境训练过程中,当小局结束时,对双方队伍给定奖励,奖励分配方式如表2 所示,1—1—2—2 表示完牌顺序分别为队伍1、队伍1、队伍2、队伍2 的选手.

Table 2 Reward Functions Designed in GuanDan Games表2 掼蛋环境训练中的奖励设计
设计的奖励方式基本与掼蛋晋级方式相同,但当掼蛋遇到等级A 时有所不同,由于当一方队伍到达等级A 时想要获胜至少要有一个队友第1 个完牌并且另一个队友不能最后一个完牌,因此若以队伍1 达到等级A 为例,完牌顺序1—1—2—2 与完牌顺序1—2—1—2 相同,剩余4 种完牌顺序奖励也相同.考虑到SDMC 方法会尽量选择高评估值的动作,因此不对奖励函数进行修正很大程度上并不会影响训练策略的正确性,故智能体在训练过程中并未对等级A 进行特殊处理.
3.3 实验结果
本节通过与不同算法的对比验证SDMC 的效果.具体而言,分别与第1 届“中国人工智能博弈算法大赛”的冠军(1stChampion)与前2 届16 强(1stTop 16和2ndTop 16)进行比较. 实验中选取2 种算法作为2支队伍,采取2 种评估指标,分别评估对战双方团队的胜利与净胜小分情况.
我们首先验证了经过30 天训练的SDMC 与其他方法的最终胜率与净胜小分,每场对战均进500 次,并重复验证5 次,最终胜率与标准差如表3 所示. 表3中的数据表示算法1 对阵算法2 时的胜率,如SDMC对抗2ndTop 16 胜率为97.5%,算法的排名顺序按照击败(胜率>50%)其他算法的顺序进行排序.

Table 3 Winning Percentage of Different Algorithms Against Each Other表3 不同算法对抗胜率 %
我们看到SDMC 对战第1 届比赛的冠军以及其他算法胜率均大于90%,对抗2ndTop 16 和1stTop 16 时胜率甚至分别大于97.5%和100%,因此可以认为SDMC 的效果显著高于其他算法. 同时我们也对比了不使用SAS 的SDMC(SDMC-无SAS)和使用SAS的SDMC 的效果,对于测试的,使用SAS 能够提升一定的SDMC 的效果.
同时对于净胜小分,我们详细列出了各种算法之间对战过程中双方小分的获得情况与净胜分,如表4 所示. 可以看到SDMC 在对战其他参赛方法的时候具有很高的3 分得分率,即在掼蛋中有很高的双上(队伍分别以上游和二游完牌)概率,在对战1stChampion 时达到44.3%,对战2ndTop 16 时达到48.4%,对战1stTop 16 时达到68.4%,因此对战过程中的净胜分非常高,对战1stChampion 时平均每局净胜达到4 955.6分. 同时观察到SDMC 与SDMC-无SAS 在对抗过程中无论是3 分、2 分、1 分的占比还是净胜分均是SDMC 更胜一筹,且SDMC 在对战除2ndTop 16 的对手时,净胜分均高于SDMC-无SAS.
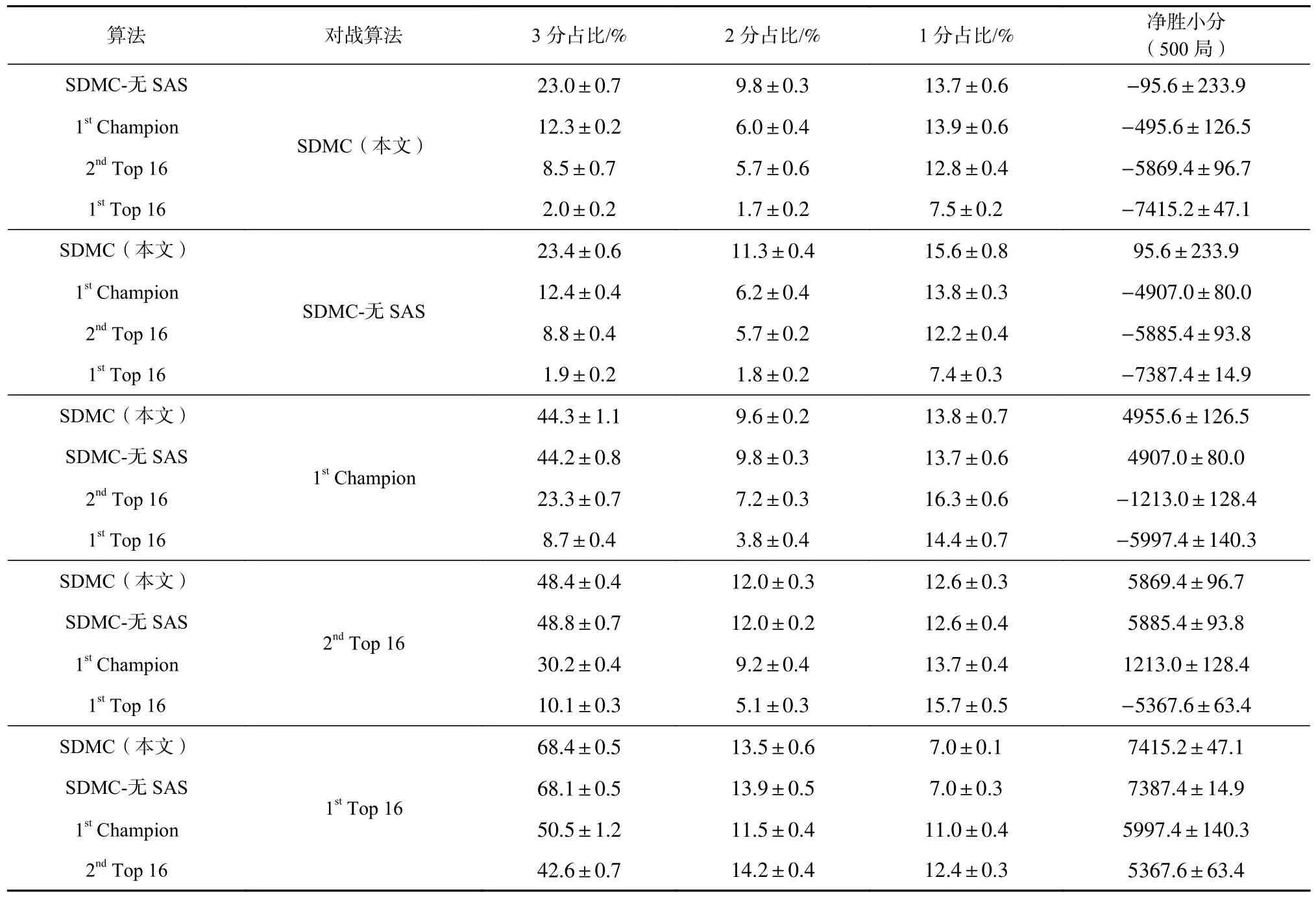
Table 4 Score of Different Algorithms Against Each Other表4 不同算法对抗时得分
最后为了验证本文提出的软启动方法的实验效果,我们比较了DMC 方法、已有策略预训练的方法(基于策略启动的DMC)以及我们提出的采用软启动的SDMC 方法对抗1stTop 16 时的胜率与平均每小局净胜分曲线,如图3 所示,其纵坐标分别为对抗的胜率与平均每小局净胜分,横坐标为训练所用的时间步. 对于每种方法,每次测试记录200 局与1stTop 16的胜率与每小局净胜分结果,测试3 次,图3 绘制了测试的平均值与标准差. 其中基于策略启动的DMC采取与DMC 和SDMC 相同的神经网络架构与训练方式,不同之处在于基于策略启动的DMC 每次自博弈生成轨迹是依据已有策略进行 ∊-贪心采样,训练基于策略启动的DMC 模型. 基于策略启动的DMC 所采用的已有策略与SDMC 相同,均为1stChampion.
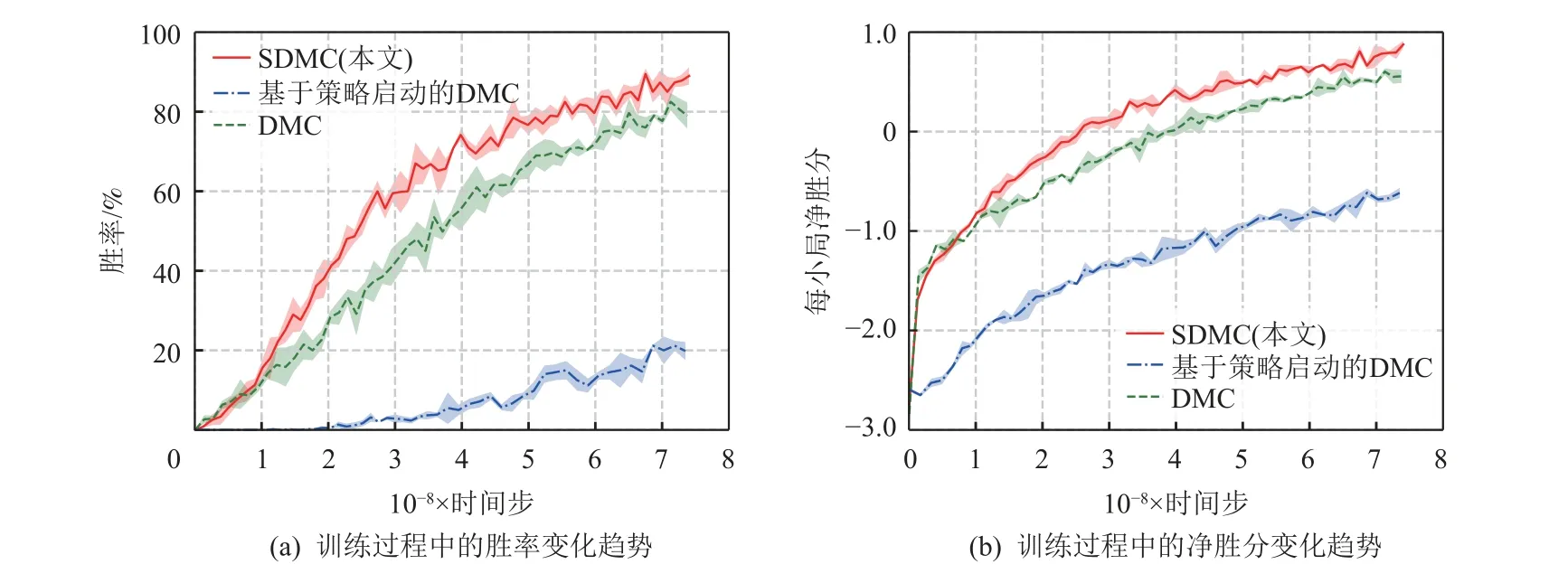
Fig.3 Performance of three methods against baseline in training stage图3 3 种方法在训练过程中对抗基准算法时的表现
从图3(a)中可以看到SDMC 相较于DMC 在训练初始阶段取得了较高的胜率提升速度,如在胜率达到60%时,SDMC 需要约2.7×108个时间步,而DMC 则需要约4×108个时间步,对于60%胜率,SDMC 仅需DMC 的68%训练开销. 同样地,在图3(b)中对于净胜小分,SDMC 仅需2.5×108个时间步即可达到净胜分大于0,而DMC 需要约3.8×108个时间步,SDMC 降低了约35%的时间需求.
同时可以发现,相比于SDMC 和DMC,基于策略启动的DMC 训练效果不佳,原因可能正如2.1 节中讨论的,仅通过已有策略生成数据在训练过程中由于掼蛋的动作空间过于庞大,因此无法很好地拟合未探索动作的值,因此存在过估计问题. 而DMC和SDMC 因为存在通过神经网络去决策的步骤,当存在高评估值的动作时,由于倾向于选择高评估值动作,可以有效地对于这个动作的评估值进行验证,从而更好地评估.
4 总 结
本文提出了一种针对掼蛋扑克博弈的软深度蒙特卡洛SDMC 方法. SDMC 方法在学习过程中不仅采用了软启动方法,结合已有策略,加速模型训练过程,同时采取软动作采样,在实际对战过程中,保证选择的策略在当前模型下的评估值变化不大的情况下对动作进行采样,降低训练过程中方差带来的影响,并增加被对手利用的难度. 在掼蛋环境下的实验表明,本文所提方法SDMC 相较于现有方法有着更高的对战胜率与净胜得分. 之后,拟从软动作采样的角度出发,依据现有模型的动作评估值,结合子博弈求解方法提升在实战环境下的策略强度,致力于得到在团体对战情况下的团队最大最小均衡等博弈论角度下的最优策略,最终实现在掼蛋等扑克博弈环境下战胜人类的职业选手.
作者贡献声明:葛振兴提出选题、研究内容,设计技术方案,撰写论文;向帅设计技术方案,采集和整理实验数据,修订论文;田品卓设计技术方案,提出指导性建议;高阳提出指导性建议,指导论文写作.

