基于动态规划法的调水工程闸泵切换优化调度方案
孟钰婕 刘吉贵 王维平 曲士松

文章编号:1671-3559(2024)01-0087-08DOI:10.13349/j.cnki.jdxbn.20230322.004
摘要:針对跨流域调水工程运行线路中经验型闸泵切换启闭形式的问题,选取位于山东省德州市中心城区潘庄引黄灌区马颊河左岸辛店闸至沟盘河水库整条线路为研究区域,基于动态规划的正向递推法,以调水线路经济最优、调水最快为目标函数分别建立2个调水过程模型;利用Python语言对2个调水过程模型进行计算,确定不同运行阶段的闸泵切换方式、开启时刻及开启时长,得到流量与水位相结合的经济优且调水快的闸泵切换优化调度方案。结果表明,沟盘河水库初始水位为影响总运行费用及总调水时间的主要因素,闸泵切换优化调度方案可使运行费用降低20%,总调水时间缩短8%,提升了调水线路的经济效益与运行效率。
关键词:优化调度;闸泵切换;动态规划法;调水过程模型
中图分类号:TV68;TV675;TV633
文献标志码:A
开放科学识别码(OSID码):
Optimal Dispatching Schemes of Gate and Pump Switching in
Water Transfer Project Based on Dynamic Programming Method
MENG Yujie1, LIU Jigui2, WANG Weiping1, QU Shisong1
(1. School of Water Conservancy and Environment, University of Jinan, Jinan 250022, Shandong, China;
2. Dezhou Riverway Management Service Center, Dezhou 253000, Shandong, China)
Abstract: Aiming at the problem of experiential gate and pumping switching station opening or closing forms in operation lines of inter-basin water transfer projects, the whole line from Xindan Gate sited on the left side of Majia River to Guopanhe Reservoir in Panzhuang Irrigation District along the Yellow River in central Dezhou city, Shandong province was selected as a research area. On the basis of forward recursive method of dynamic programming, two water transfer process models were established with objective functions of optimal economy and the fastest water transfer of water transfer routes. The two water transfer process models were calculated by using Python language to determine gate and pump switching modes, starting instants, and starting time at different operating stages, and economical and fast water transfer optimal dispatching schemes of gate and pump switching combined with flow and water level were obtained. The results show that the initial water level of Goupanhe Reservoir is the main factor affecting the total operating cost and the total water transfer time. The optimal dispatching schemes of gate and pump switching can reduce the operating cost by 20%, shorten the total water transfer time by 8%, and improve the economic benefits and operating efficiency of the water transfer lines.
Keywords: optimal dispatching; gate and pump switching; dynamic programming method; water transfer process model
收稿日期:2022-10-20 网络首发时间:2023-03-23T15:05:56
基金项目:山东省自然科学基金项目(ZR2021ME069)
第一作者简介:孟钰婕(1998—),女,山东枣庄人。硕士研究生,研究方向为土木水利。电话: 15254156231, E-mail: meng199803@126.com。
通信作者简介:王维平(1961—), 男, 山东滕州人。 教授, 博士, 博士生導师, 研究方向为水资源与水环境、含水层补给管理。E-mail:
stu_wangwp@ujn.edu.cn。
网络首发地址:https://kns.cnki.net/kcms/detail/37.1378.n.20230322.1408.008.html
我国社会经济发展迅速,水资源需求量日益增加,加剧了水资源短缺的问题[1]。跨区域调水是缓解水资源供需矛盾、实现水资源科学配置、促进区域协调发展的有效措施[2]。调水线路中的泵站、闸门等水工建筑物是调水过程的核心枢纽,在整个跨流域调水工程的成本及效率方面起到了关键性的作用[3-4]。调度人员仅凭借经验调节闸门及泵站的启闭情况,使调水线路的运行效率很难达到最佳,从而造成能源浪费[5]。依据优化模型计算出闸泵切换方案,优化调水线运行,可提高调水工程的效益。
在经济效益方面,有许多学者针对泵站及闸门的优化问题展开了相关研究[6-8]。黄草等[9]以垸和片区为基本配水单元,构建地区多闸泵系统水资源优化配置模型,使得区域缺水范围大幅缩小,缺水时间大幅缩短,补水工程效益显著。钱睿智等[10]建立城区河网水动力-水环境模型,根据实测资料并结合模型演算,优化了现有闸泵联合调度方式。目前,依据不同闸门及泵站的特性,提升调水工程经济效益的优化算法有很多,例如遗传算法[11]、改进粒子群优化算法[12]、多目标粒子群算法[13]、动态规划法[14]等。其中,动态规划法在优化调水线路闸门及泵站方面应用较少,但可以更好地反映多级闸泵切换形式,并得到最优解,形成优化调度方案。本文中以山东省德州市中心城区调水工程为例,以向沟盘河水库调水为目标,结合调水线路中所有的水工建筑物,从运行功率与流量角度分别建立经济最优模型、调水最快模型,利用动态规划法调整调水状态和供水规则。最终根据德州市中心城区调水现状,结合经济最优模型及调水最快模型得到经济优且调水快的闸泵切换优化调度方案,为调水线路的高效运行提供参考。相对于目前单纯的闸门控制调度或泵站控制调度而言,本文中将提出在引黄时间有限的情况下德州市中心城区调水工程中流量与水位结合的闸泵切换的运行方式。
1 研究对象概况
1.1 区域概况
德州市地处山东省西北部,海拔约为32.6 m,属于温带季风气候,降水量较少且分布不均,年平均降水量约为554.8 m,属于缺水地区。德州市中心城区人口约7万,地区生产总值约为8×1011元,主要依靠引蓄黄河水来满足城区各类用水需求。为了解决德州市中心城区缺水问题,于2009年开启穿减河引黄调水工程,由潘庄灌区的引黄总干渠向马颊河引水,经马颊河左岸处的辛店闸引水至沟盘河水库,以完成整个调水过程。
潘庄引黄灌区涉及德州市德城、武城、禹城、平原、陵县、夏津、宁津、齐河等8个区、县(市),总控制面积为5 851 hm2。春灌时期由于农耕用水和生活用水需求突出,因此须开启潘庄闸引调黄河水,每年2—7月份和10—12月份进行调水(冰期、汛期不引水),其中2—7月份为主要调水时段,每年引水5~7次,每次引水时间约为30 d。调水工程面临如何在引黄闸开启时间内将黄河水引入调蓄水库的问题。
1.2 调水线路运行方式
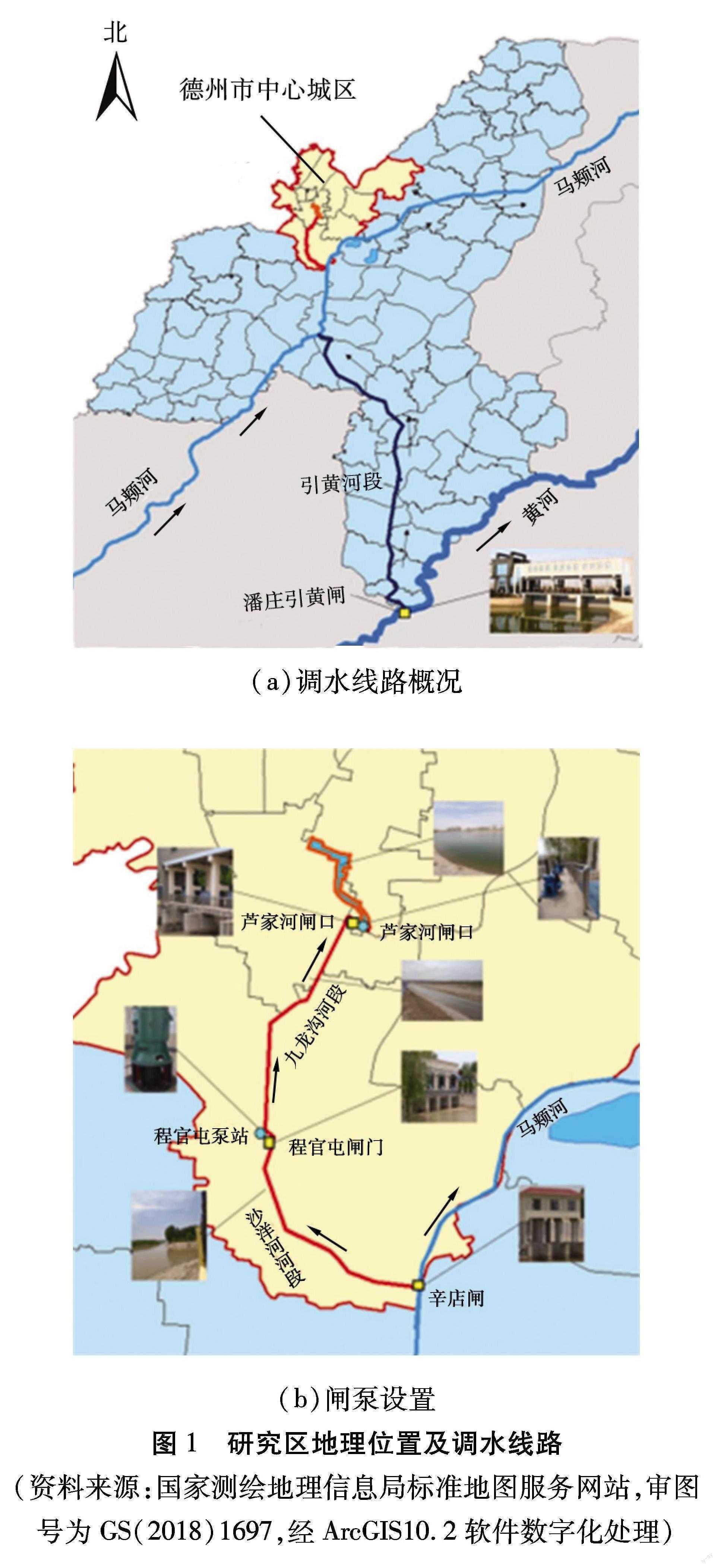
本研究中的调水线路如图1所示。 将黄河水由潘庄灌区进入马颊河, 再由马颊河左岸辛店闸进入沙杨河(河口宽度为60 m, 河面宽度为18 m, 长度为8 400 m), 经程官屯扬水站进入九龙沟(河口宽度为30 m, 河底宽度为6 m, 长度为9 060 m)、再经芦家河扬水站进入沟盘河水库调蓄后向德州市第三水厂供水, 日供水量为105 m3, 输水线路总长度为17.46 km。 程官屯扬水站与芦家河扬水站处既设立闸门又设立泵站,闸与泵合一,以满足利用闸门自流输水或泵站提水输水2种不同情况的调水方式。 泵站输水流量大, 时间短, 耗能多;闸门输水流量小, 时间长, 不耗能。 整个调水线路中设置了自动化控制设备, 在库区安装监控设备, 可及时读取调水前后水位、流量数据。 本线路每年调水9次左右, 每次运行时间为7 d, 单次调水量约2.7×106 m3。每年2—7、10—12月份进行引水,为居民生活供水。沟盘河水库库容约5.5×106 m3(兴利水位为20.5 m),死库容为3×106 m3(死水位为17.9 m),居民日供水量为105 m3,占据整个城市供水量的67%。
2 调水过程模型
2.1 数据来源
调水过程模型的建立基于调水时间、调水量及其不同的需水条件。调水线路的计算数据及规则如下:
1) 程官屯扬水站处设有4台立式轴流泵,单机功率为180 kW,单机提水体积流量为2.5 m3/s,当程官屯闸前水位达20.5 m时泵站或闸门开启,向九龙沟河段输水。
2)芦家河扬水站处自流闸宽度、高度均为
3 m, 单孔;设有2台潜水轴流泵, 单机提水体积流量为2.5 m3/s, 单机配套功率为200 kW, 运行电费C为0.6 元/(kW·h)。当芦家河闸前水位达21 m时, 选择开启此处的闸门或泵站, 向沟盘河水库输水。
3)当沙扬河河道及九龙沟河道所蓄水量满足沟盘河水库的剩余库容时关闭辛店闸,直至沟盘河水库水位达到21 m时调水结束。
4)程官屯与芦家河处闸门及泵站只保留一种开启形式,不存在闸门与泵站共同开启的情况。闸门与泵站的切换根据程官屯及芦家河处的闸门自流流量大小来判断。考虑运行费用时,须在整条线路调水正常的前提下尽量不开启泵站;考虑调水时长时,当过闸流量小于泵站提水流量时就要开启此处泵站。
其他数据如下:
1)九龙沟处农业灌溉区在灌溉期间农业需水量约为2.035×105 m3;
2)沙杨河河道渗漏量约为3.36×104 m3,九龙沟河道渗漏量约为3.08×104 m3。
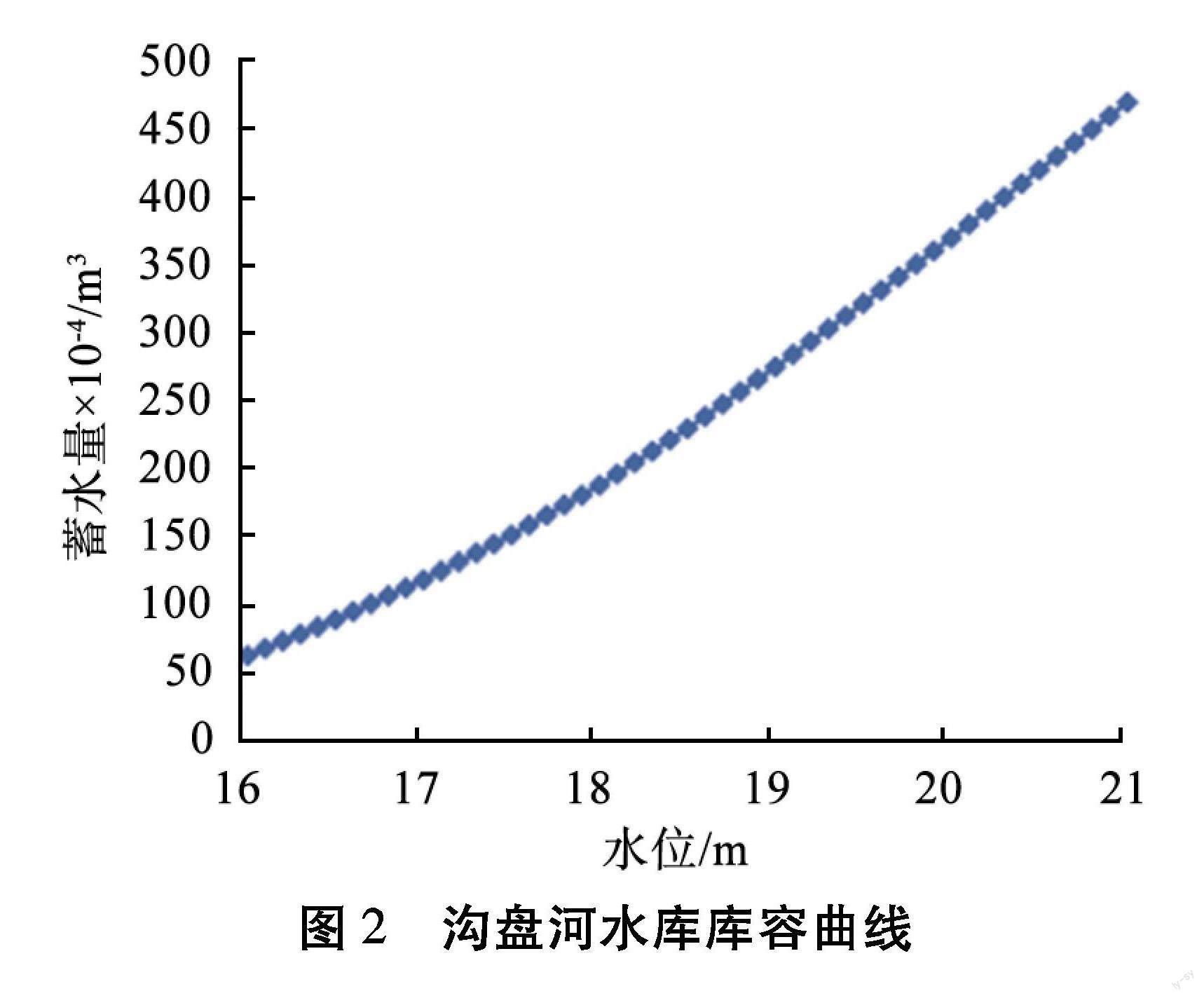
3)沟盘河水库向居民日供水量约为105 m3, 水库库容曲线如图2所示。 沟盘河水库开始调水时的水位为17.9~19.0 m, 当水位低于17.9 m时停止供水;当水位高于19.0 m时, 水库蓄水量较多, 无须调水。
2.2 模型建立
本研究共涉及2个优化目标,分别为经济最优目标和调水最快目标,根据这2个目标,结合调水过程,对调水、供水规则及外调水量进行优化,根据研究区工程组成现状建立目标函数,在不同调水时段与不同节点处设立决策方式,利用动态规划的正向递推法进行计算,结合Python语言循环计算,最终得到满足目标函数的优化结果。基于实际调水工况的动态规划路线如图3所示。
2.2.1 经济最优模型
在考虑经济最优的情况下,由于调水过程中的运行费用来源于泵站开启后产生的电费,因此将运行费用最少作为目标函数。经济最优模型旨在最大
限度地降低输水过程的成本,即在每个阶段处根据决策变量正向判断,使得各阶段都满足运行费用最低的条件,以达到优化调水过程的目的。经济最优模型如下:
1)阶段变量i。将整个调水过程简化为4个阶段:阶段i=1为水流经辛店闸;阶段i=2为水流至程官屯扬水站;阶段i=3为水流至芦家河扬水站;阶段i=4为水流入沟盘河水库。
2)决策变量为阶段i处闸门或泵站的输水功率Pi。其中闸门的输水功率为0,泵站的输水功率依据泵的类型而定。
时段运行费为第i阶段输水功率为Pi时产生的运行费用Wi,计算公式为
Wi(Pi, ti)=Pi ti C ,(1)
式中ti为第i阶段的输水运行时间。
3)状态变量Si,即为第i阶段处的输水功率。Si≥Pi,即在阶段状态的范围内,决策者可以选择无功率(闸门),2、4台泵功率。根据图3中的動态规划路线,各阶段可选择的最大决策集合为
S1={A}, S2={B1,B2,B3}, S3={C1,C2}, S4={D},其中A、B1、B2、B3、C1、C2、D为辛店闸开启、程官屯闸门开启、程官屯2台泵开启、程官屯4台泵开启、芦家河闸门开启、芦家河2台泵开启、沟盘河水库蓄水。
设立总调水过程中运行费用最小的目标函数,表达式为
f1=min∑4i=1Wi ,(2)
式中f1为总调水过程中的总运行费用。
4)系统状态转移方程,即
Si-1=Si-Pi 。(3)
5)总功率约束,即
∑4i=1Pi=Pt≤Pa ,(4)
式中Pa、Pt分别为整个调水系统的最大运行功率、总运行功率。
6)依据决策变量与状态变量,采取动态规划正向计算,递推方程可表示为
Fi(Si)=mini=1,2,3,4{Wi(Pi, ti)+Wi+1(Si-Pi )} ,
Fi(Si)=Wi(Pi)(5)
式中:Fi(Si )为调水过程中以各阶段经济最优方式输水所产生的运行费用;Wi(·)为第i阶段
产生的运行费用。
2.2.2 调水最快模型
在考虑调水最快的情况下,需保证每阶段的过水流量最大才能满足要求,即转化为单位时间内调水量最大作为目标函数。调水最快模型旨在使在最短时间内完成整个调水过程,即在每个判断调水状况的阶段处选择单位时间内所调水量最大的选项,结合动态规划法,最大程度地缩短输水时间,以达到优化整体调水速度的目的。调水最快模型如下:
1)阶段变量k。整个调水阶段简化为4个阶段k:阶段k=1为水流过辛店闸;阶段k=2为水流至程官屯扬水站;阶段k=3为水流至芦家河扬水站;阶段k=4为水流入沟盘河水库。
2)决策变量为处于k阶段处的闸门或泵站的体积流量Qk。闸门处过水流量依据宽顶堰过流公式进行推导,泵站的过水流量则依据泵的类型及开启情况而定。
宽顶堰过流公式为
Qk=σεαB2g H320 ,(6)
式中:σ为淹没系数;ε为侧收缩系数;α为流量系数;B为宽顶堰总宽度;H0是堰上总水头。
单位时间内断面处的过水总体积Vk的计算公式为
Vk(Qk, tk)=Qk tk ,(7)
式中tk为第k阶段的过水时间。
3)状态变量Ik即为第k阶段处的过水体积流量。Ik≥Qk,即在阶段状态的范围内,决策者可以选择闸门,2、4台泵的开启形式。根据图3中的动态规划线路,各阶段可选择的最大决策集合为
I1={A}, I2={B1,B2,B3 }, I3={C1,C2}, I4={D}。
设立总调水过程中调水最快的目标函数,表达式为
f2=∑4k=1Vk ,(8)
式中f2为总调水过程中的总调水体积。
4)系统状态转移方程,即
Ik-1=Ik-Qk 。(9)
5)各阶段流量约束,
Qk,min 式中Qk,min、Qk,max为第k阶段所允许的最小过流量、最大过流体积。 6)河道水量平衡约束,即 Wk+1=Xk+Wk-Pk-Fk ,(11) 式中Wk、Xk、Pk、Fk为第k阶段处河道的蓄水量、来水量、出流量、河道损失量。 7)各河段蓄水量约束,即 0≤V0+Qk1Δtk1-Qk2Δtk2≤Vmax ,(12) 式中:V0为输水前各河段渠道内的初始蓄水量;Vmax为各河段渠道内设计水位条件下最大蓄水体积;Qk1Δtk1为第k阶段的入流体积;Qk2Δtk2为第k阶段下游的出流体积。 8)沟盘河水库水量约束,即 Vded≤V0+QkΔtk-Qk,supΔtk≤Vuti ,(13) 式中:Vded为水库的死库容;V0为水库初始水量, m3;Vuti为水库的兴利库容,即水位达到21 m;QkΔtk为第k阶段内流入水库的水量;Qk,supΔtk为第k阶段内水库供水量。 9)利用动态规划正向计算,递推方程可表示为 Fk(Dk)=maxk=1,2,3,4 {Vk(Qk, tk)+Vk+1(Dk-Qk )}, Fk(Dk)=Vk(Qk ),(14) 式中:Fk(Dk )为调水总过程的最大调水量;Vk(·)为第k阶段过水体积流量。 3 调水过程模型结果分析 利用Python語言对经济最优模型、调水最快模型进行计算,以确定不同运行阶段下闸泵切换方式、开启时刻及开启时长。由于沙杨河河段、九龙沟河段及沟盘河水库的初始水位皆为变量,因此在优化计算时,采取单变量对比法比较沙洋河河段、九龙沟河段及沟盘河水库初始水位对整个调水过程各阶段时长的影响。因为辛店闸处体积流量为16 m3/s(实测流量),几乎不变,所以在研究不同河段初始水位及沟盘河水库初始水位对整个调水过程的影响时,默认另一河段初始水位为17.5 m,沟盘河水库初始水位为18.5 m。 3.1 经济最优模型结果分析 计算不同河段及水库不同初始水位时的调水优化结果,可得总调水时间的变化情况,如图4所示。 由图可知:总调水时间随河段及水库初始水位的升高呈现下降趋势, 但沟盘河水库初始水位的变化相较于2个河段初始水位变化为总调水时间的最大影响因素。 当沟盘河水库初始水位变化时, 总运行费用变化也最大, 水库初始水位为17.9 m时, 运行费用为4.85×104元;水库初始水位为19.0 m时, 运行费用为3.52×104元。 在九龙沟河段与沙扬河河段初始水位变化情形下, 总运行费用分别为(4.21~4.26)×104、(4.20~4.28)×104元, 数值相差小, 基本呈水平线分布。 由此证明沟盘河水库初始水位变化为整个总调水运行费用的最大影响因素。 3.2 调水最快模型结果分析 沙扬河河段、九龙沟河段及沟盘河水库初始水位变化计算结果如图5所示。由图可知:随着河段及水库的初始水位升高,每个调水阶段时间均呈现缩短趋势。除九龙沟河段初始水位变化对程官屯闸门开启时间影响较为明显以外,其他闸门及泵站的开启时间均对九龙沟河段及沙杨河河段初始水位的变化敏感度不高,沟盘河水库初始水位变化仍为总调水过程的最大影响因素。在沙扬河河段、九龙沟河段、沟盘河水库初始水位为18.0~18.2 m时,由于沟盘河水库的可用水量较少,因此各泵站与闸门开启的时长随沟盘河水库水位变化的幅度较小,此时沟盘河水库水位对闸门及泵站的影响要小于九龙沟河段;随着水库初始水位逐渐增高,水库的可用库容迅速增加,逐渐超越了九龙沟河段及沙杨河河段初始水位变化对于各调水过程带来的影响。 对比经济最优模型与调水最快模型可知, 在调水最快模型的情形下, 各泵站开启时间远长于经济最优模型情形下的泵站开启时间。 这是因为当处于调水最快模型的情形下, 闸门处自流流量小于泵站输水流量时,直接切换为开泵的运行方式,从而缩短了总调水时间。 由泵站开启时间可计算出运行费用, 在调水最快模型中, 沟盘河水库初始水位从17.9 m升至19.0 m时的运行费用从5.36×104元降至4.56×104元, 沙杨河初始水位从17.5 m升至19.0 m时的运行费用从5.42×104元降至5.35×104元,九龙沟初始水位从17.5 m升至19.0 m时的运行费用从5.54×104元降至5.37×104元。 经过对比, 调水最快情形下产生的运行费用比经济最优情形下产生的运行费用要高出约20%, 均来自于为保持调水最快而延长了泵站开启时间所带来的用电消费。 4 闸泵切换优化调度方案与实例分析 研究区域未经优化的3次经验型调水过程如表1所示。 综合图4、5可知, 调水过程中缩短泵站的开启时间就可以提高整个调水过程的经济效益, 但考虑到调水时间有限制, 应将经济最优模型和调水最快模型进行综合优化, 得到经济尽可能优的情形下的快速调水方式。 综合考虑经济效益和调水效率, 程官屯处与芦家河处的闸门和泵的开关形式也需要改变。 在综合考虑经济效益及调水速度的情形下进行调水的过程中, 过闸流量不宜太小, 也不能为保证调水速度而一直开启泵站, 应将调水时间及调水速度综合考虑, 及时切换泵站开启的状态。 根据沟盘河水库不同初始水位计算得到经济优且调水快的闸泵切换优化调度方案如表2所示。 由表可知, 经济优且调水快的闸泵切换优化调度方案的调水时间较图4中的经济最优结果缩短了约6%, 运行费用较图5中的调水最快结果减少了约7%, 属于两者结合后的优化调水结果。 对比表1、2可知, 经济优且调水快的闸泵切换优化调度方案的总运行费用为4.24×104~5.11×104元, 总调水时间为129.1~159.0 h,较未经优化的调水过程总运行费用减少了约20%,总时间缩短了约8%。由此证明,相较于未经优化的经验型调水过程,闸泵切换优化调度方案在经济性与及时性方面均得到提高,验证了经济优且调水快的闸泵切换优化调度方案的可行性。 5 结论 本文中依据现有的闸泵切换方式复杂的问题,以经济最优、调水最快为目标,通过构建基于动态规划法的闸泵切换优化调水模型,求解出研究区调水线路结合经济效益与运行效率的经济优且调水快的闸泵切换优化调度方案,得到以下主要结论: 1)经济优且调水快的闸泵切换优化调度方案对比经济最优模型计算结果,总调水时长缩短了约6%;对比调水最快模型计算结果,总运行费用减少了约7%;对比未经优化的调水结果的总调水时长缩短了约8%,总运行费用减少了约20%。 2)河段及水库调水前的初始水位影响总调水过程中的闸门与泵站的开启时间及总运行费用,但沟盘河水库的初始水位变化引起较大的调水量变化,相较于沙扬河河段与九龙沟河段初始水位变化,为总调水过程中的最大影响因素。 3)经济最优模型与调水最快模型后續还应结合调水工程水位与流量自动监测进一步完善的条件下,提高该工程实时优化调度的能力,保障德州市中心城区供水工程高效、安全运行。 参考文献: [1]YU M, WANG C R, LIU Y, et al. Sustainability of mega water diversion projects: experience and lessons from China[J]. Science of the Total Environment, 2018, 619/620: 721. [2]MA Y S, CHANG J X, GUO A J, et al. Optimizing inter-basin water transfers from multiple sources among interconnected river basins[J]. Journal of Hydrology, 2020, 590: 1. [3]刘新征. 跨流域调水技术经济问题研究: 以位山闸引黄调水为例[D]. 泰安: 山东农业大学, 2010. [4]薛萍, 卢龙彬, 雷晓辉, 等. 基于遗传算法的单级泵站机组流量优化分配模型[J]. 济南大学学报(自然科学版), 2022, 36(6): 675. [5]CHEN W P, TAO T, ZHOU A J, et al. Genetic optimization toward operation of water intake-supply pump stations system[J]. Journal of Cleaner Production, 2021, 279:1. [6]郭永灵, 张海晨, 朱兴林. 基于动态规划法的单级泵站日经济运行优化模型[J]. 中国农村水利水电, 2020(1): 192. [7]董加新, 王智, 王玉川, 等. 多级泵站系统能耗的计算方法[J]. 中国农村水利水电, 2021(5): 43. [8]曹晨星, 赵春龙, 翟超, 等. 水电站进水口快速闸门设计分析与优化[J]. 西北水电, 2022(2): 71. [9]黄草, 刘启, 付蔷, 等. 洞庭湖北部地区多闸泵系统水资源优化配置模型及应用研究[J]. 长沙理工大学学报(自然科学版), 2022, 19(2): 37. [10]钱睿智, 陈静, 李章林, 等. 扬州市中心城区河网闸泵联合调度优化研究与应用[J]. 江苏水利, 2019(12): 18. [11]卓灵. 南方地区“一库两站”复杂水资源优化配置模型的改进遗传算法研究[D]. 扬州: 扬州大学, 2022: 33-37. [12]吴海龙. 强排自排一体化闸站控制调度研究与应用[D]. 扬州: 扬州大学, 2022: 15-20. [13]赵靓芳. 城市河道流域的排水系统内涝模拟及河道闸泵的优化调度模型研究[D]. 广州: 华南理工大学, 2019: 45-52. [14]张利婷, 袁保惠. 应用动态规划法对单泵装置的实时控制[J]. 内蒙古水利, 2011(3): 145. (责任编辑:于海琴)

