空间向量在解答立体几何问题中的运用

葛学清

(山东省日照第一中学)

立体几何是高考中的必考题目且分数占比较高.由于立体几何问题有抽象、复杂等特性,学生在解题中,往往存在着多种多样的问题,导致解题效率不高,而借助空间向量解题有时可以降低立体几何问题的解题难度,因此,本文将结合实际问题,分析空间向量在解答常见立体几何问题时的应用.

1 在距离问题中的运用

例1 如图1所示,四边形ABCD,EADM和MDCF均是边长为a的正方形,点P是ED的中点.

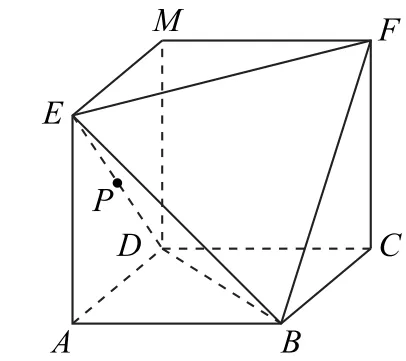
图1

(1)求点D到直线BF的距离;(2)求点P到平面EFB的距离.

如图2所示,以

图2

DA,DC,DM所 在直 线 为x轴、y轴、z轴,建立空间直角坐标系,则有D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),M(0,0,a),E(a,0,a),F(0,a,a),由中点的坐标公式得

2 在角问题中的运用

在立体几何问题中,有诸多关于角的问题都可以借助空间向量进行解答:如在二面角问题的解答中,首先要建立合适的空间直角坐标系,然后找到二面角所涉及的两个平面,接着通过法向量进行求解,最后观察二面角是钝角还是锐角,从而得到最终答案.同样地,可以借助空间向量将线面角转化为线线角进行解答.

例2 如图3 所示,在正四 棱 柱ABCD-A1B1C1D1中,AB＝2,AA1＝4.

图3

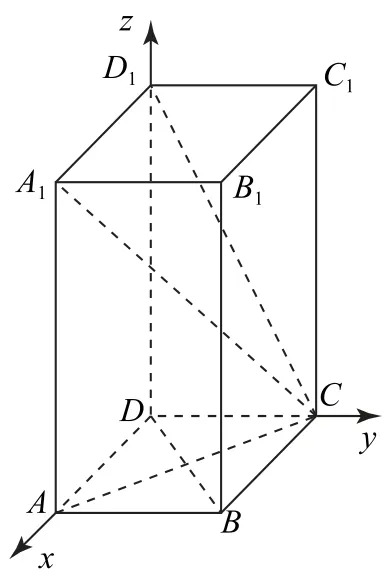
图4

(1)求证:BD⊥A1C;

(2)求二面角A-A1C-D1的余弦值.

3 在位置关系中的运用

空间几何的线面关系(垂直或平行)问题是常见考点,在求解这类问题时,同样可以借助空间向量进行解答.比如在线面平行的证明中,可以通过建立合理的空间直角坐标系,求出平面外一条直线的方向向量l与平面的法向量n,当l•n＝0时,则可证得线面平行.

例3 如图5所示,在四棱 锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底 面ABCD,PA＝AD＝CD＝2AB＝2,M为PC的中点.

图5

图6

(1)求 证:BM// 平面PAD;

(2)平面PAD内是否存在一点N,使得MN⊥平面PBD? 若存在,确定N的位置;若不存在,说明理由.

综上,平面PAD内存在点),使得MN⊥平面PBD.

本文介绍了使用空间向量法解答立体几何问题,不难发现灵活运用空间向量法,能够降低诸多立体几何问题的解题难度,从而有效提升解题效率.

(完)