空间中以平行关系为背景的题型及求解策略

张 平

(广东省珠海市实验中学)

空间中的平行关系是立体几何中重要的位置关系,是“线线平行”“线面平行”“面面平行”三种关系的统称,是高考考查的热点.试题呈现方式主要有两类:一是旗帜鲜明地证明平行关系;二是以平行关系为背景进行综合考查.本文针对第二类问题结合具体题目进行剖析,以期帮助读者突破思维难点,提升抽象思维能力.

1 客观性试题赏析

1.1 以线线平行为背景

例1 在棱长为10的正方体ABCD-A1B1C1D1中,一条平行于A1C的直线与正方体的表面交于P,Q两点,其中P在侧面ADD1A1上,且到A1D1的距离为3,到AA1的距离为2,则点Q所在的面是( ).

A.平面ABCDB.平面ABB1A1

C.平面BCC1B1D.平面CDD1C1

方法1 如图1所示,连接A1P并延长与线段AD交于点E,则平面A1PC∩平面ABCD＝EC.又PQ//A1C,P在平面A1PC上,则PQ⊂平 面A1PC,所 以Q在EC上,即点Q在平面ABCD上,故选A.

图1

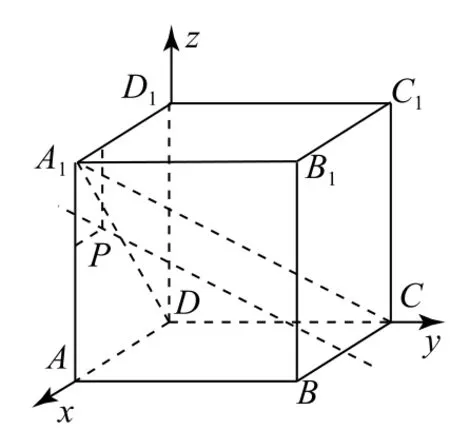
图2

10时,t＝－8或2;当－t＝0或10时,t＝0或－10;当t＋7＝0或10时,t＝－7或3.只有t＝－7满足题意,此时点Q(1,7,0)在平面ABCD内,故选A.

本题命题视角比较新颖,方法1通过作图将问题转化为平面问题,方法2则通过坐标法及点在平面内的坐标要求进行定性求解,突出空间问题平面化的处理方法.

1.2 以线面平行为背景

例2 在棱长为2的正方体ABCD-A1B1C1D1中,点M是该正方体表面及其内部的一动点,且BM//平面AD1C,则动点M的轨迹所形成区域的面积是_____.

如图3所示,在棱长为 2 的 正 方 体ABCD-A1B1C1D1中,动 点M满足BM//平面AD1C,由面面平行的性质可得当BM始终在一个与平面AD1C平行的面内时满足题意.连接A1B,BC1,A1C1,则平面A1BC1//平面AD1C,所以平面A1BC1满足题意,且△A1BC1是边长为2 2的等边三角形,则

例3 已知正方体ABCD-A1B1C1D1的棱长为1,点E,F分别是线段AB,BD1上的动点,若EF//平面ADD1A1,则三棱锥A-EFB1体积的最大值为( ).

如图4 所示,由题意得DD1⊥平面ABCD,则 平 面BDD1⊥平面ABCD.在平面BDD1内过F作FG⊥DB于G,则FG⊥平 面ABCD,从 而FG//DD1,则FG//平 面ADD1A1.又EF//平 面ADD1A1,EF∩FG＝F,则 平 面EFG//平 面ADD1A1,从而EG//AD,所以EG⊥平面AEB1.又FG//DD1//AA1,FG⊄平 面AEB1,则FG//平 面AEB1,所以点F到平面AEB1的距离等于点G到平面AEB1的距离.设BE＝x(0＜x＜1),则GE＝BE＝x,即点F到平面AEB1的距离等于x,且,所以

图4

例4 已知正四面体ABCD的棱长为1,棱AB//平面α,则正四面体上所有点在平面α内的射影构成的图形面积的取值范围是_________.

根据正四面体的特性,易知AB⊥CD且异面直线AB与CD之间的距离为.将正四面体ABCD绕棱AB旋转,当棱CD//平面α时,CD在平面α内的射影最长,记为GH,此时正四面体上所有点在平面α内射影构成的图形面积最大,且

在CD绕AB旋转的过程中,CD在平面α内的射影越来越短,当CD⊥平面α时,C,D在平面α内的射影重合,所得的射影图形是以AB为底,异面直线AB与CD之间的距离为高的三角形,此时射影构成的图形面积最小,即,所以此正四面体上所有点在平面α内的射影构成的图形面积的取值范围是

动态问题是立体几何中的一个难点,关键是要挖掘“运动中的不变量”,求解例2的关键是通过定点B作平面AD1C的平行平面来确定点M的轨迹;例3则通过三棱锥的等体积转化将突破点调整为求点F到平面ABB1A1的距离;例4则将AB,CD之间在“运动中的不变量”体现得淋漓尽致.

1.3 以面面平行为背景

例5 (2016年全国Ⅰ卷文理11)平面α过正方体ABCD-A1B1C1D1的顶点A,α//平面CB1D1,α∩平面ABCD＝m,α∩平面ABB1A1＝n,则m,n所成角的正弦值为( ).

如图5 所示,设平面CB1D1∩平面ABCD＝m′,平面CB1D1∩平面ABB1A1＝n′,由α//平面CB1D1,可得m//m′,n//n′,则m,n所成角等于m′,n′所 成 角.过 点D1作D1E//B1C交AD的延长线于点E,连接CE,则直线CE即为m′.连接A1B,过点B1作B1F1//A1B交AA1的延长线于点F1,则直线B1F1即为n′.连接BD,则BD//CE,B1F1//A1B,则m′,n′所成角即为A1B与BD所成角,即m,n所成角为60°,其正弦值为,故选A.

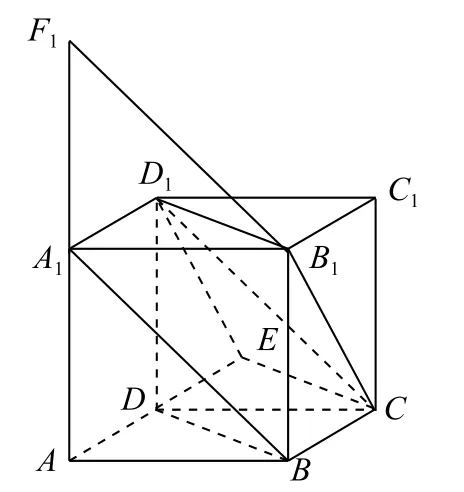
图5

例6 (2018年全国Ⅰ卷理12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( ).

方法1 平面α与正方体的每条棱所在直线所成的角都相等,只需与过同一顶点的三条棱所成的角相等即可.如图6所示,若AP＝AR＝AQ,则平面PQR与正方体过点A的三条棱所成的角相等.若点E,F,G,H,M,N分别为相应棱的中点,易证得平面EFGHMN平行于平面PQR,且六边形EFGHMN为正六边形.因为正方体的棱长为1,所以正六边形EFGHMN的边长为,可得此正六边形的面积为,从而所求截面的最大面积为,故选A.

图6

图7

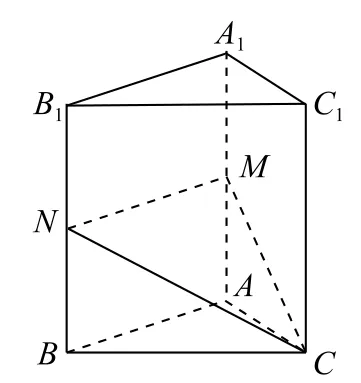
图8

图9

方法2 由方法1易知平面PQR与平面ABCD的夹角为定值α且tanα＝2.设截面的面积为S,截面在平面ABCD内的射影图形面积为S′,则由,可知S′越大,则S越大.

例6的两种方法体现了选择题的两种思路,方法1是从截面的特殊位置出发去计算结果得到答案,方法2则是从解答题的角度给出了严格的计算及推理,具有严密性.实质上还可以将六边形EFGHMN分成两个等腰梯形求解面积.

2 综合试题赏析

2.1 以线线平行为背景

例7 已知正三棱柱ABC-A1B1C1的底面面积为S,高为h,过点C作与三棱柱的底面ABC成α)角的截面MNC,使MN//AB,求截面的面积.

2.2 以线面平行为背景

例8 (2019年北京卷文18)如图10所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底部ABCD为菱形,E为CD的中点.

图10

(1)求 证:BD⊥平面PAC;

(2)若∠ABC＝60°,求 证:平 面PAB⊥平面PAE;

(3)棱PB上 是 否 存在点F,使得CF//平面PAE? 说明理由.

(1)(2)求解过程略.

(3)方法1 (先猜后证)存在点F为PB的中点时,满足CF//平面PAE.

如图11所示,分别取PB,PA的中点F,G,连接CF,FG,EG, 在△PAB中,FG//AB且;在菱形ABCD中,E为CD的中点,所以CE//AB且CE＝,则CE//FG且CE＝FG,即四边形CEGF为平行四边形,所以CF//EG.又CF⊄平面PAE,EG⊂平面PAE,所以CF//平面PAE.

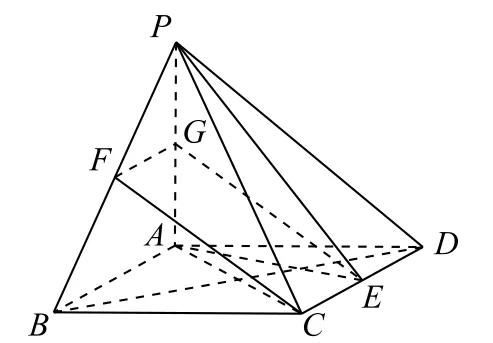
图11

方法2 (转化为面面平行)假设棱PB上存在点F,使得CF//平面PAE.如 图12 所 示,过 点F作FH⊥AB于H,连接CH,易证FH//PA,从而FH//平面PAE,由CF∩FH＝F,知平面FHC//平面PAE.又平面FHC∩平面ABCD＝CH,平面PAE∩平面ABCD＝AE,则CH//AE.又AH//CE,从而四边形AECH为平行四边形,由E为CD的中点,可知点H为AB的中点,从而点F为PB的中点,即存在点F为PB的中点时,满足CF//平面PAE.

图12

方法3 (转化为线线平行)假设棱PB上存在点F,使 得CF//平 面PAE.如 图13 所 示,过 点F作FM⊥PA于M,连接EM.易证FM//AB//CE,从而F,M,C,E四 点 共 面.由CF//平 面PAE及 平 面FMEC∩平面PAE＝ME,可得CF//ME,从而四边形FMEC为平行四边形,则FM＝CE.由E为CD的中点,知,从而点F为PB的中点,即存在点F为PB的中点时,满足CF//平面PAE.

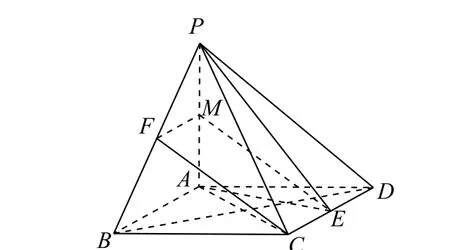
图13

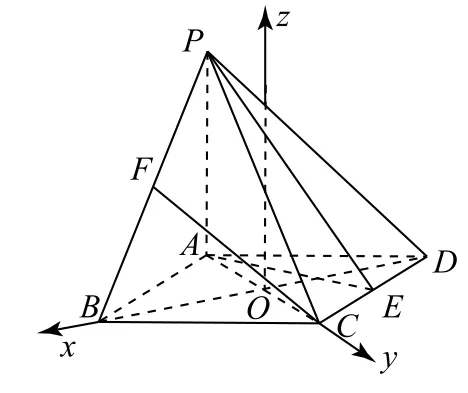
图14

方法5 (坐标法)假设棱PB上存在点F,使得CF//平面PAE.设AC与BD相交于O,由四边形ABCD为菱形,可得AC⊥BD且点O为AC与BD的中点.

例7的特点在于对问题的分类讨论,例8则是借助于一题多解对此类问题的解决策略进行了全方面总结与呈现,完善与丰富了此类问题思考途径.

限于篇幅,此处省略了对以面面平行为背景的试题剖析.从上述试题可以看出:对空间中平行关系的考查是全方位的,试题形式灵活,方法多样,在复习过程中,要及时进行题型与解题策略的归纳总结,充分发挥“微专题”的优势,帮助并引导学生形成知识网络与框架,提升数学素养.

(完)