立体几何动态问题的求解策略

王 慎

(甘肃省定西市渭源县第四高级中学)

立体几何的动态问题,历来是高考的热点与难点,这类集策略性、挑战性与创新性于一体的考题,常常令考生“望而生畏”,因此研究这类问题的求解策略意义重大.这类动态问题主要包含动点变化、平面图形的翻折、几何体的平移和旋转问题等,由此引发的常见题型有动点轨迹、角度与距离的计算、面积与体积的计算以及有关几何量的最值求解等.那么,求解这类问题有何策略? 本文举例说明.

1 去枝除叶现本质

立体几何动态问题的本质是研究空间点、线、面的位置关系,因此面对复杂的图形,我们应排除各种干扰,捕捉最简单的具有实质性意义的点、线、面的有关信息,抓住问题的本质,从而从看似无序的图形中找到规律,这是解决“动态”问题的关键.

例1 如图1 所示,在正 方 体ABCD-A′B′C′D′中,点P在线段AD′上运动,设异面直线CP与BA′所成角为θ,则cosθ的最小值是______.

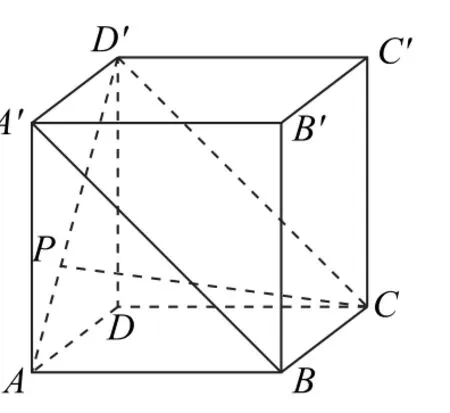
图1

本题考查正方体的结构特征及异面直线所成角的定义,因此只需抓住问题的本质,发现CP与A′B所成角即为CP与D′C所成角θ,于是可得出θ的取值范围,进而得到最小值.

2 极端位置显神奇

对于某些以填空题形式出现的立体几何“移动”问题,要求某个变量的取值范围,不妨依据图形变化的连续性,从极端位置中发现取值范围的上限与下限,进而得出答案.

例2 如图2所示,在棱长为1 的正方体ABCDA1B1C1D1中,点E,F分 别是棱BC,CC1的中点,P是底面ABCD(含边界)上一动点,满足A1P⊥EF,则线段A1P 长度的取值范围是_____.

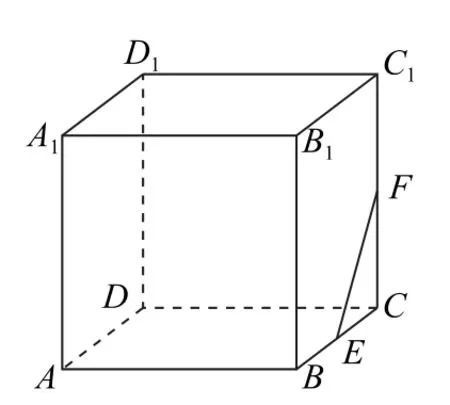
图2

如图3 所示,连接BC1,A1D,A1C,则EF//BC1,所以A1D⊥BC1,A1D⊥EF.又DC⊥EF,所以EF⊥平面A1DC,故当P在线段CD上运动时,有A1P⊥EF.

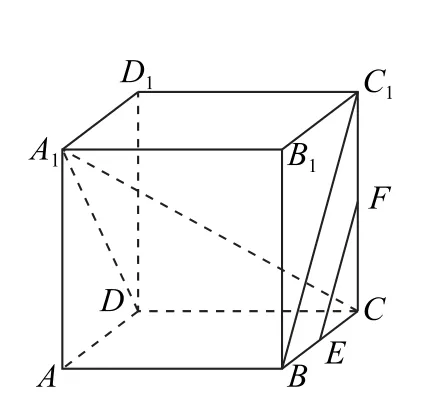
图3

当P与D重合时,A1P有最小值2,当P与C重合时,A1P有最大值,则线段A1P长度的取值范围是

由于A1是定点,而P是底面ABCD(含边界)上一动点,故只需找到P在底面ABCD(含边界)上的极端位置,问题便迎刃而解.

3 翻折问题找垂面

求解立体几何翻折动态问题的关键是找到图形变化过程中的“不变因素”,比如,若能抓住相关线或面的垂面,化空间为平面,那么问题的突破口便跃然纸上.

例3 如图4所示,在等腰直角△ABC中,AB＝BC＝8,D为AC的中点,l为平面ABC内过点D的一条动直线,沿直线l进行翻折,点C在翻折过程中记为点C′,C′在直线l上的射影为C1,C′在平面ABC上的射影C2落在直线AB上,则当取得最小值时,C1到直线AB的距离为_________.

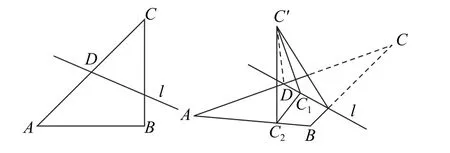
图4

C′C2⊥平面ABC,l⊂平面ABC,则C′C2⊥l,而C′C1⊥l,C′C1∩C′C2＝C′,所以l⊥平面C′C1C2,于是C1C2⊥l,因此点C2,C1,C三点 共 线,|CC1|＝|C′C1|＞|C1C2|.以直 线AB,BC分 别 为x轴、y轴 建 立 平 面 直 角 坐 标 系,如 图5 所 示,则A(－8,0),C(0,8),D(－4,4),依题意,直线l的斜率存在且不为0.设直线l的方程为y＝k(x＋4)＋4,直线CC1的方程为,则C2(8k,0),且

图5

由|C′C1|＞|C1C2|,得|2k2＋k＋1|＜|k－1|,解得－1＜k＜0.因此,有

对于平面图形翻折问题,我们应注意在翻折过程中位于同一平面内的点线的位置关系和数量关系的不变性.

4 轨迹问题探定值

立体几何中的轨迹问题是一类与解析几何有关的动态问题,而解析几何中的曲线具有“动中有定”的特点,因此探求立体几何轨迹问题,就是探寻变化过程中的不变关系.

例4 如图6 所示,在直三 棱 柱ABC-A1B1C1中,△ABC是边长为2 的正三角形,AA1＝3,N为棱A1B1上的中点,M为棱CC1上的动点,过N作平面ABM的垂线段,垂足为点O,当点M从点C运动到点C1时,点O的轨迹长度为__________.

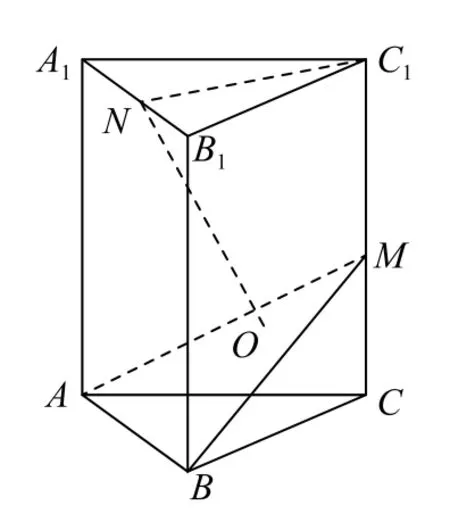
图6

图7

图8

本题要求点O的轨迹的长度,需先探究O的轨迹形状,于是采用数形结合的方法发现点O是以PN为斜边的直角三角形的直角顶点,因此它到PN的中点的距离是PN的一半,它的轨迹是圆的一部分.

(完)