NATURALLY REDUCTIVE (Q1, a2)METRICS*

Ju TAN(谭举)School of Microelectronics and Data Science，Anhui University of Technology,Maanshan 243032,China E-mail : tanju200r@163.com

Ming XU(许明)+School of Mathematical Sciences，Capital Normal University，Beijing 100048，China E-mail: mgmgmgxu@163.com

In this paper, we discuss natural reductiveness in Finsler geometry, which has been given from different view points, by Latifi in [22], and by Deng and Hou in [9].

The equivalence between these two definitions was proven in [36].It should be remarked that, unlike the situation in Riemannian geometry, the Finslerian natural reductiveness cannot be implied from the normal homogeneity, and in some sense, it is even stronger, because naturally reductive Finsler metrics are Berwaldian.

The first goal of this paper is to characterize the natural reductiveness of non-Riemannian(α1,α2) metric.The (α1,α2) metrics are defined in [12].We believe that these generalize Randers metrics [26] and (α,β)-metrics [23], and they share some similar properties [1, 12, 34,35].The f-product in [5] is a special case of the Berwald (α1,α2) metric; it is defined as a Finsler metric F = f(α1,α2) on M1×M2, where each αiis a Riemannian metric on Mi.A general(α1,α2) metric can be similarly presented as F =f(α1,α2), but each αiis only defined on a (possibly non-integrable) distribution Viin T M with T M =V1+V2.

From a geometric point of view, we prove the following explicit and simple description:

Theorem 1.1Any non-Riemannian naturally reductive homogeneous (α1,α2) metric is locally isometric to an f-product between two naturally reductive Riemannian metrics.

For connected and simply connected manifolds,the local f-product description in Theorem 1.1 is global and the inverse of Theorem 1.1 is valid (see Corollary 3.3).With some minor changes, the proof of Theorem 1.1 might argue in favour of a similar description for the non-Riemannian naturally reductive (α,β) manifold.

Notice that naturally reductive Finsler metrics are Berwald[9].These results are consistent with to Szab´o’s description for Berwald metrics, i.e., they are some local “product” among Riemannian manifolds and non-Riemannian affine symmetric spaces[29].Here the speciality of the (α1,α2) metric type specifies how the “product” is built and constrains the product factor and the factor number.

Switching to the algebraic point of view,we prove that if the non-Riemannian homogeneous(α1,α2) metric F is defined using the homogeneous Riemannian metric α, then the natural reductiveness of F is in fact inherited from α (see Corollary 3.4).This byproduct generalizes the corresponding result for (α,β) metrics (see [25, Theorem 3.7]).Meanwhile, we see that a non-Riemannian homogeneous (α1,α2) manifold (M,F) may achieve its natural reductiveness for diffferent homogeneous space representations M = G/H.The assertion that M is locally an f-product does not imply that G is also locally a product (see Example 3.6).

The second task of this paper is to discuss the curvature properties of a homogeneous(α1,α2) manifold.The S-curvature was found by Shen when he proved the volume comparison theorem in Finsler geometry [27].The Hessian of the S-curvature S(x,y) for its y-entries essentially provides the mean Berwald curvature (E-curvature in short).E-curvature helps us study the celebrated Landsberg Conjecture [17].In general Finsler geometry, there are many properties related to the S-curvature(for example, the vanishing, constant,isotropic and weakly isotropic S-curvature conditions), and there are many others related to the E-curvature(for example, the vanishing, constant and isotropic E-curvature conditions).These properties are closely related,and some are equivalent in homogeneous Finsler geometry[33].If we specify the homogeneous metric to be of Randers or(α,β) type, even more equivalences can be proven([6, 11, 30]).We transport these observation to homogeneous (α1,α2) metrics and prove the following theorem:

Theorem 1.2For a homogeneous (α1,α2) metric, the following are equivalent:

(1) it has weakly isotropic S-curvature;

(2) it has vanishing S-curvature;

(3) it has isotropic E-curvature;

(4) it has vanishing E-curvature.

Flag curvature generalizes sectional curvature in Riemannian geometry [2], but its calculation in general and homogeneous Finsler geometry is much harder.However, for a naturally reductive Finsler metric, the vanishing of the spray vector field greatly simplifies the homogeneous flag curvature formula [16].For a naturally reductive (α1,α2) metric of the form F =αφ(α2/α), we present an explicit flag curvature formula (see Theorem 4.4).

The arrangement of the rest of this paper is as follows: in Section 2, we summarize some preliminaries in general and homogeneous Finsler geometry.In Section 3, we prove Theorem 1.1.In Section 4,we prove Theorem 1.2 and calculate the flag curvature formula for a naturally reductive (α1,α2) metric.

2 Preliminaries

In this section, we summarize some fundamental knowledge on general Finsler geometry from [2, 28], and recall the basic settings of homogeneous Finsler geometry in [7].The notion of the (α1,α2) metric is from [12].

2.1 Minkowski Norms and Finsler Metrics

Definition 2.1LetVbe a finite dimensional real vector space.A Minkowski norm onVis a continuous function F :V→[0,+∞) satisfying the following properties:

(1) regularity: F is positive and smooth onV{0};

(2) positive 1-homogeneity: F(λy)=λF(y) for any y ∈Vand λ ≥0;

(3) strong convexity: for any y ∈V{0}, the fundamental tensor

Definition 2.2A Finsler metric on a smooth manifold M is a continuous function F :T M →[0,+∞) such that

(1) F is smooth on the slit tangent bundle T M{0};

(2) the restriction of F to each tangent space TxM is a Minkowski norm.

We also call the pair (M,F) a Finsler manifold or a Finsler space.

For example, a Finsler metric is Riemannian when the fundamental tensor (gij(x,y)) depends on x ∈M only, for any standard local coordinate x = (xi) ∈M and y = yi∂xi∈TxM,or, equivalently, the Cartan tensor

vanishes everywhere.

A Randers metric has the form F = α+β, where α is a Riemannian metric and β is a one-form with a pointwise α-norm smaller than 1.An(α,β)metric has the form F =αφ(β/α),where φ(s) is a positive smooth function of one variable.

A Minkowski norm or a Finsler metric is said to be reversible if opposite (tangent) vectors have the same length.Obviously, all (α1,α2) metrics (including Riemannian metrics) are reversible, and most (α,β) metrics (including Randers metrics) are not.The (α,β) and (α1,α2)metrics can achieve the maximal non-Euclidean linear symmetry degree in each tangent space,i.e., O(n -1) and O(n1)×O(n2), respectively, where n = n1+n2is the dimension of the manifold.Thus the calculation and formulae for these metrics have relatively low complexity.

2.2 E-curvature, S-curvature and Flag Curvature

For a Finsler manifold (M,F), the geodesic spray is the smooth tangent vector field G on T M, which can be locally presented as

for any standard local coordinate.

We say that (M,F) has weakly isotropic S-curvature if there exists a function c(x) and a one-form ∊on M such that

is satisfied at every (x,y) ∈T M.We say that a weak isotropic S-curvature metric F is isotropic, if the one-form ∊in (2.2) vanishes.We say that an isotropic S-curvature metric F is of constant or vanishing S-curvature if we further have c(x)≡const or c(x)≡0, respectively.

Remark 2.3In this paper, the S-curvature is always with respect to the B.H.measure.Generally speaking, this can be defined for any smooth measure on a Finsler manifold.Some S-curvature properties, like the vanishing, constant or isotropic S-curvature properties, depend on the choice of the smooth measure,and others,like the weakly isotropic S-curvature property,does not.

On a Finsler manifold (M,F), the flag curvature is defined for each flag triple (x,y,P)with x ∈M, y ∈TxM{0} and a tangent planeP⊂TxM containing y.Suppose thatP=span{y,v}.Then the flag curvature of this triple is

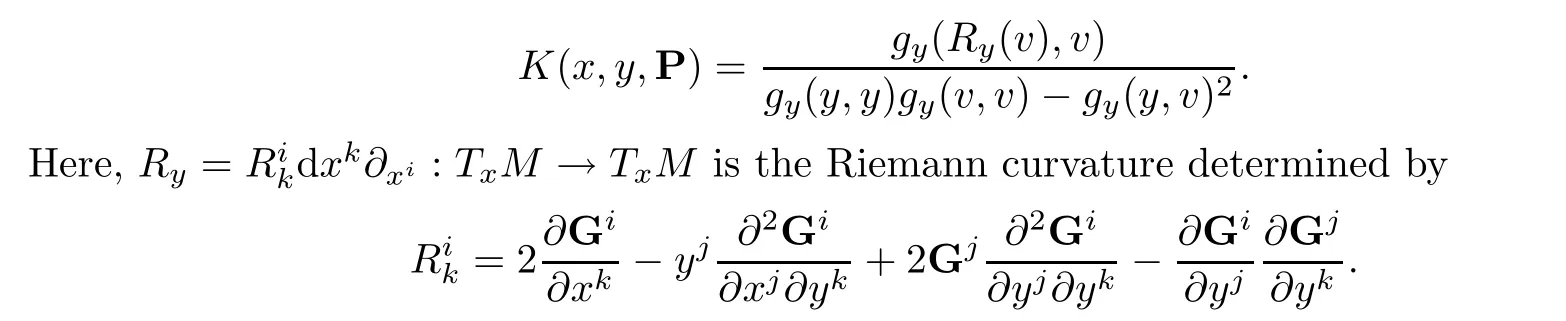
2.3 Homogeneous Finsler Space

Let (M,F) be a Finsler manifold.We call (M,F) or F homogeneous if the isometry group I(M,F) acts transitively on M [7].Since I(M,F) is a Lie transformation group [10, 24], we may present M as the smooth coset space G/H for any Lie subgroup G in I(M,F), where H ={g ∈G|g·o=o} is the isotropy subgroup at o=eH ∈G/H.

Denote that g = Lie(G) and h = Lie(H).Since the G-action on M is effective, H is compactly imbedded, so we can find an Ad(H)-complement m of h in g,i.e., a reductive decomposition g =h+m for G/H.In the Lie algebraic level, this means that [h,m] ⊂m.Generally speaking, reductive decompositions for G/H are not unique.

A chosen reductive decomposition g=h+m helps us study the homogeneous geometry of G/H because m can be canonically identified as the tangent space To(G/H),which is equivariant in the sense that the Ad(H)-action on m coincides with the isotropy action on To(G/H).Any vector v ∈g can be decomposed as v =vh+vm,according to the given reductive decomposition;its m-summand coincides with the evaluation V(o) for the vector field V induced by v ∈g, i.e.,A homogeneous Finsler metric F on G/H can be one-to-one determined by its restriction F(o,·)to To(G/H)=m,which is an arbitrary Ad(H)-invariant Minkowski norm(for simplicity,we still use the same F to denote this norm).The homogeneous metric F is Riemannian if and only if it provides an Ad(H)-invariant Euclidean norm |·|=〈·,·〉1/2on m.For a homogeneous metric F on G/H, the vector field induced by any v ∈g is a Killing vector field.

When studying the local geometry of a homogeneous Finsler manifold, we may assume the connectedness and simple connectedness for M = G/H, and the connectedness for both G and H.In this context, a homogeneous (α1,α2) metric on G/H can be determined by any arbitrary Ad(H)-invariant (α1,α2) norm on m.An Ad(H)-invariant (α1,α2) norm on m can be determined by the following procedure: first, we choose an Ad(H)-invariant Euclidean norm α on m, and an Ad(H)-invariant and α-orthogonal decomopsition m =V1+V2with each ni= dimVi> 0.Next, we choose some positively 1-homogeneous smooth real function L:[0,+∞)×[0,+∞)→[0,+∞)(the requirements for the function L are implied by Theorem 3.2 in [12] or Theorem A in [32]).Then the desired norm can be presented as

2.4 Natural Reductiveness

In homogeneous Riemannian geometry, the natural reductiveness is defined as follows [19]:

Definition 2.4The homogeneous Riemannian manifold (M,g) or the metric g is called naturally reductive for the homogeneous space representation M =G/H with G ⊂I(M,g)and the reductive decomposition g=h+m if

or, equivalently,

Here 〈·,·〉 is the Ad(H)-invariant inner product on m induced by g.

In this definition, the natural reductiveness for a homogeneous Riemannian manifold is more like an algebraic property, because it depends on the representation M = G/H and the decomposition g=h+m.This can also be more geometrized as follows:

Definition 2.5The homogeneous Riemannian manifold (M,g) or the metric g is called naturally reductive if there exists a homogeneous space representation M = G/H with G ⊂I(M,g) and a reductive decomposition g=h+m such that (2.3) or (2.4) is satisfied.

Notice that Definition 2.4 specifies the precise choices for the homogeneous space representation and the reductive decompostion, and that Definition 2.5 only concerns their existence.

In homogeneous Finsler geometry, there are several equivalent definitions or descriptions for natural reductiveness.The first one was proposed by Latifi [22].

Definition 2.6The homogeneous Finsler manifold (M,F), or the metric F, is called naturally reductive for the homogeneous space representation M = G/H with G ⊂I(M,F)and the reductive decomposition g=h+m if we have that

The second definition was proposed by Deng and Hou [9].

Definition 2.7The homogeneous Finsler manifold (M,F), or the metric F, is called naturally reductive for the homogeneous space representation M = G/H with G ⊂I(M,F)and the reductive decomposition g = h+m if there exists a homogeneous Riemannian metric g on M = G/H such that g has the same connection as F, and its natural reductiveness is achieved for the given decomposition.

The equivalence between Definition 2.6 and Definition 2.7 was proven in [36].Naturally reductive Finsler manifolds (or metrics), without mentioning the homogeneous space representation or the reductive decomposition, can be similarly defined as Definition 2.5.From Definition 2.7, we can immediately see that a naturally reductive Finsler metric is Berwald.

Huang [16] provided an equivariant description using his spray vector field.For a homogeneous Finsler manifold (G/H,F) with a reductive decomposition g = h+m, the spray vector field η :m{0}→m is the Ad(H)-invariant smooth map determined by

Then a homogeneous Finsler manifold (G/H,F) is naturally reductive for a given reductive decomposition if and only if the corresponding spray vector field is constantly 0 [9, 16].

Remark 2.8To be more self contained, here we briefly recall the proof in [36] for the equivalence between Definition 2.6 and Definition 2.7.In [9], Theorem 3.2 proved that Latifi’s natural reductiveness implies Deng-Hou’s, and Theorem 3.1 indicated that Deng-Hou’s natural reductiveness implies η ≡0.To prove Latifi’s natural reductiveness from η ≡0, we consider the smooth vector field W(y) = adm(w)y = [w,y]mfor any w ∈m, and denote that ρt=exp(t·adm(w)) is the one-parameter subgroup W generates in GL(m).When η ≡0, W is tangential to the indicatrix F = 1.Thus each ρtis a linear isomorphism preserving F, which is called a linear isometry for F in [35].A linear isometry for F is automatically an isometry for the Hessian metric gyon m.Therefore the generating vector field W is a Killing vector field for (m,gy), which is the meaning of (2.5) in Definition 2.6.

3 Proof of Theorem 1.1

Lemma 3.2Keeping all the above assumptions and notations, then we have

(1) each ki=h+miis a Lie subalgebra of g, i.e., [mi,mi]⊂h+mifor i=1,2;

(2) [m1,m2]⊂h;

(3) for any yi∈mi, 〈yi,[yi,mi]mi〉=0, where the subscript midenotes the projection with respect to decomposition ki=h+mi.

From(3.3),we see that[mi,mi]⊂h+mifor each i,and that[m1,m2]⊂(h+m1)∩(h+m2)=h.This proves (1) and (2) in Lemma 3.2.

Now we are ready to prove Theorem 1.1.

Proof(When H is connected) We identify each mias a subspace in To(G/H).Then we have the G-invariant distribution Vi= ∪g∈Gg∗(mi) ⊂T(G/H) on G/H.The decomposition m=m1+m2is orthogonal with respect to the inner product 〈·,·〉=α2(·), so the linear bundle decomposition T(G/H)=V1+V2is orthogonal at each point with respect to the homogeneous Riemannian metric α on G/H.

First, we prove that each Viis integrable.The first claim in Lemma 3.2 provides the Lie subalgebra ki=h+mi.Let Kibe the Lie subgroup of G generated by ki.Then H is a closed subgroup in Kiand the submanifold Ki/H is the integral submanifold of Vipassing o.Using the homogeneity, we see that Vigenerates the smooth foliation {gKi/H,∀g ∈G} on G/H.

Second, we consider the restriction of α to Ki/H, which is the homogeneous metric determined by the Euclidean norm αi|mi.For simplicity, we denote (Ki/H,αi) as this homogeneous Riemannian submanifold.Obviously ki= h+miis a reductive decomposition for Ki/H, and by (3) in Lemma 3.2, (Ki/H,αi) is naturally reductive with respect to this decomposition.

Next,we prove that each submanifold gKi/H is a totally geodesic submanifold in(G/H,α).Any vector v ∈g induces a Killing vector field V on (G/H,α).In particular, when the vector v is from mi, V is tangential to Ki/H, and V(o) = v ∈m = To(G/H).For any w ∈m2and any Killing vector fields X,Y corresponding to u,v ∈m1, respectively, we have that

in which ∇αis the Levi-Civita connection of α.By (1) and (2) in Lemma 3.2, each summand on the right-hand side of (3.4) vanishes.This implies that the second fundamental tensor for K1/H in (G/H,α) vanishes at o.Using the G-actions, we see that the second fundamental tensors of all gK1/H vanish everywhere.For gK2/H, the argument is similar.

To summarize, we have two integrable totally geodesic foliations V1and V2, which are α-orthogonal complements of each other, at each point of G/H.Thus (M,α) is locally a Riemannian product between integral submanifolds of V1and V2.

Finally,we only need to prove that the integral submanifold of Viis naturally reductive.By the G-invariancy, we only need to consider Ki/H, i.e., the integral submanifold of Vipassing o.The restriction of α to Ki/H is the homogeneous Riemannian metric αidetermined by the Euclidean norm αion mi.Obviously, ki=h+miis a reductive decomposition for Ki/H, and by (3) in Lemma 3.2, (Ki/H,αi) is naturally reductive for this decomposition.

(When H is not connected) Denote H0as the identity component of H.Then g=h+m is also a reductive decomposition for G/H0and (G/H,F) is locally isometric to (G/H0, ˜F), in which the homogeneous metric ˜F is determined by the same (α1,α2) norm on m as F.Thus(G/H0, ˜F) is also a homogeneous (α1,α2) manifold and it is naturally reductive with respect to the same decomposition as F.We have just proven that(G/H0, ˜F)is locally isometric to an f-product between two naturally reductive Riemannian manifolds, so the same claim is valid for (G/H,F) immediately.□

For a connected and simple connected manifold,Theorem 1.1 can be strengthened as follows:

There are many examples of naturally reductive (α1,α2) manifolds.For example, when each Gi/Hiis a normal homogeneous Riemannian manifold, the f-product metric on G1/H1×G2/H2is naturally reductive.Most of these metrics are not Riemannian, locally Minkowski,or symmetric.

We also have the following byproduct:

Remark 3.5The natural reductiveness of a non-Riemannian (α1,α2) metric F on G/H does not imply the local product decompositions G = G1×G2and H = H1×H2such that G1/H1and G2/H2are the two factors in the local f-product representation for F.Here is an example:

4 Curvatures of Homogeneous (α1,α2) Manifolds

4.1 Proof of Theorem 1.2

The S-curvature curvature formula of a homogeneous manifold is the following(see Theorem

4.2 in [33] and Proposition 4.6 in [16]):

Theorem 4.1Let G/H be a smooth coset space with a reductive decomposition g =h+m.Then, for any homogeneous Finsler F and an invariant smooth measure,the S-curvature S(o,·):m{0}=To(G/H){0}→R is determined by

where η is the spray vector field and Iyis the mean Cartan tensor.

Using Theorem 4.1, we can prove

Lemma 4.2Let G/H be a smooth coset space with a reductive decomposition g=h+m,and let the decomposition m=m1+m2be used for defining the homogeneous (α1,α2) metric F on G/H.Then, for any nonzero vector y ∈m1∪m2⊂m=To(G/H), the S-curvature S(o,y)vanishes.

ProofSince F is a homogeneous (α1,α2) metric, the corresponding Minkowski norm F =F(o,·) on m is invariant for a standard block-diagonal action of O(n1)×O(n2) such that m1and m2are the fixed point sets of the O(n2)and O(n1)-actions,respectively.Because of this symmetry, the Cartan tensor vanishes on(m1∪m2){0}(the detailed argument is contained in the proof of Lemma 2.2 in [35]).Thus for any nonzero y ∈m1∪m2, Iy(·)≡0, and by Theorem 4.1, S(o,y)=Iy(η(y))=0.□

Now we prove Theorem 1.2.

ProofThe equality (3.19) in [4] points out that

from which we see that

i.e., a Finsler metric has weak isotropic S-curvature if and only if it has isotropic E-curvature.This observation proves (2)⇒(4) and (3)⇒(1) immediately.The statement (4)⇒(3) is trivial,so we only need to prove (1)⇒(2).

Let(G/H,F)be a homogeneous(α1,α2)manifold with weakly isotropic S-curvature.Suppose that g = h + m is a reductive decomposition for G/H and that the decomposition m = m1+m2is used when defining F.Since F is reversible, its S-curvature S(x,y) is odd for the y-entry, i.e., S(x,y)+S(x,-y)≡0.Then the property of weakly isotropic S-curvature,S(x,y)=(n+1)c(x)F(x,y)+∊(x,y), for some function c(x)and one-form ∊(x,y),provides that

i.e., c(x) ≡0 and S(x,y) = ∊(x,y).By Lemma 4.2, S(o,·) vanishes on (m1∪m2){0}.Then,by the linearity of S(o,·)=∊(o,·), S(o,·) vanishes at any nonzero y ∈m=m1+m2.Using the homogeneity, we see that (G/H,F) has vanishing S-curvature.□

Remark 4.3Theorem 4.2 in [12] provides an explicit S-curvature formula for a homogeneous (α1,α2) metric.We may use this to observe directly that the S-curvature S(o,·) is odd and vanishes on (m1∪m2){0}.Theorem 4.3 in [12] provides the algebraic characterization of the vanishing S-curvature property for a homogeneous (α1,α2) metric; i.e., a homogeneous(α1,α2)metric F on G/H with a reductive decomposition g=h+m has vanishing S-curvature if and only if

where the inner product〈·,·〉=α2(·)and the decomposition m=m1+m2are used for defining F.By Theorem 1.2, (4.2) also characterizes the properties of vanishing E-curvature, isotropic E-curvature, etc..

4.2 Flag Curvature of a Naturally Reductive (α1,α2) Manifold

where [R(x,y)y]2denote the components of R(x,y)y in m2.

According to Theorem 2.1 in [8], the Riemann curvature Ry(x) at o ∈(G/H,F) is given by

Thus, we obtain that

Substituting (4.4)–(4.10) into

we complete the proof.□

Conflict of InterestThe authors declare no conflict of interest.