控制类课程群视角下案例教学初探
高学辉 刘瑞国
(山东科技大学 智能装备学院,泰安 271019)
自动化、电气工程及其自动化、电气工程与智能控制等专业往往开设的控制类课程有“自动控制原理”“现代控制理论”以及“智能控制”等课程。这类课程具有的一个共同的特点就是寻找合理的控制输入使得被控系统在稳定的前提下获得期望的输出。“自动控制原理”主要从频域角度采用传递函数模型出发解决上述问题。“现代控制理论”则是从时域角度采用状态空间模型解决问题。“智能控制”在以上两门课程学习的基本方法之上,对传递函数或状态空间描述的线性或非线性系统,采用更加先进、智能的控制策略,寻找合适的控制输入在保证系统稳定的前提下获得期望的输出。本文将这类具有共同特征又各有特点,且课程内容具有延续性的课程称之为课程群,将以上三门课程称之为控制类课程群。
单独的控制课程教学研究已经取得了大量的成果[1-6]。文献[1]基于一致性建构原则进行了以学生为中心、以成果为导向的“自动控制原理”课程的教学设计,从五个方面包括优化课程目标、设计学习活动等改进了新的思路,并以多功能机器人为例作贯穿式工程实物实训。文献[2]采用开放式评价方法进行了疫情下的“现代控制理论”教学研究并取得了较好的结果。文献[3]在“智能控制”课程教学中引入PBL教学模式,以寻迹小车仿真为例设计了PBL模糊控制教学案例,探讨了开展PBL案例教学的设计步骤与实施方法,增强了学生学习兴趣,提高了学生分析解决问题的能力,但是以上从课程群角度探讨教学方法、教学内容等的教学研究却几乎无人涉及。本文将从控制类课程群的角度,以案例教学为例初探控制类课程群教学问题。
以RLC电路为案例贯穿“自动控制原理”“现代控制理论”和“智能控制”课程,对“自动控制原理”的传递函数建模、零极点配置、根轨迹分析等知识点,“现代控制理论”的传递函数和状态空间的转换、能控性能观性判据、零极点配置、状态观测器以及李雅普诺夫稳定性分析等知识点,“智能控制”的神经网络控制、滑模控制、自适应控制等知识点进行了串联,从课程群的角度以纵向视角通过RLC电路这个案例说明了各门课程之间的延续关系,让学生更加深入地理解学习的内容,做到学以致用,举一反三,增强理论联系实际的能力,提高分析问题、解决问题的水平。
1 “自动控制原理”教学案例
首先以案例教学探索“自动控制原理”课程教学方法。在“自动控制原理”课程中,系统模型的建立的知识点往往会采用RLC电路作为案例引入,如图1所示。本文以此最简单最常见案例为例从控制类课程群角度贯穿“自动控制原理”“现代控制理论”和“智能控制”三门课程,探索在课程群视角下的案例教学。

图1 RLC无源网络
图1中RLC电路可以得到其微分方程模型如式(1)所示:
(1)
从式(1)的二阶微分方程出发,首先从传递函数的角度对“自动控制原理”中零极点配置等知识点应用本案例教学设计。
考虑式(1)微分方程,对方程中各项做拉普拉斯变换可得:
(LCs2+RCs+1)Uc(s)=Ur(s)
(2)
根据传递函数的定义,可以得到RLC电路的传递函数为:
(3)
为了说明RLC电路案例在“自动控制原理”课程零极点配置知识点的教学应用,假设L=100 H,C=0.002 F,R=300 Ω。则RLC电路的传递函数为:
(4)
若希望将极点配置到[-3 -5],直接配置法或串联前馈矫正法都可以将传递函数配置到[-3 -5]。
下面给出Matlab仿真程序和结果。Matlab仿真程序如下:
clc;clear;closeall;
num =[0,0,1];
den =[0.2,0.6,1];
G0 = tf(num,den)
disp(‘开环极点’);pole(G0)
G1 = feedback(G0,1)
disp(‘闭环极点’);pole(G1)
P =[-3,-5];%期望极点
%% 1.传递函数极点配置
%设G_c = p0 + p1*s
%由 D(S) = 1 + G_c*G0 = 0;
%和 F(S) = (s + 3)*(s + 5) = 0
% D(s) = F(s),可以求出p0 和 p1
%校正传函
G_c = 1*tf([1,2],[0,1])
%校正后传函
G_o = G_c*G0
%闭环
G2 = feedback(G_o,1)
disp(‘串联校正后闭环极点’);pole(G2)
step(G2)
其阶跃响应如图2所示,配置[-3 -5]后的根轨迹如图3所示。
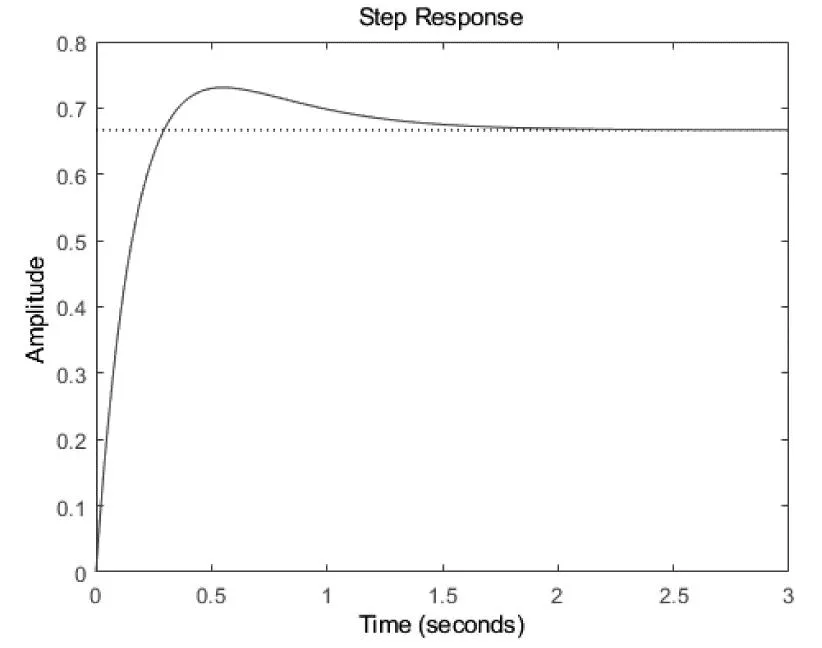
图2 传递函数极点配置后阶跃响应

图3 传递函数极点配置根轨迹图
同样可以容易地做出Bode图,分析输入电压ur(t)和电容两端输出电压uc(t)之间的关系。本案例可囊括“自动控制原理”中多个知识点,比如传递函数模型的建立、零极点配置、根轨迹分析以及冲激和阶跃响应等等。
从课程群的角度来看,“自动控制原理”分析的案例可以容易地应用到“现代控制理论”中,只是不再采用传递函数方法在频域下分析,而是将传递函数转换为状态空间形式,采用“现代控制理论”的知识进行分析,这样就将“自动控制原理”和“现代控制理论”从课程群的角度串在一起。
2 “现代控制理论”教学案例
如前所述,从课程群的角度可将分属于不同课程的内容串在一起考虑,更加有助于课程的学习和理解。仍然以上节RLC电路为例说明。首先根据“现代控制理论”的知识点,可以将传递函数转换为状态空间方程,因此,传递函数(4)可以转换为:
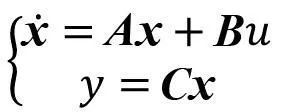
(5)
其中

在状态空间的形式下仍然可以将系统极点配置到[-3 -5],在状态空间下的Matlab程序如下:
clc;clear;closeall;
num =[0,0,1];
den =[0.2,0.6,1];
G0 = tf(num,den)
disp(‘开环极点’);pole(G0)
G1 = feedback(G0,1)
disp(‘闭环极点’);pole(G1)
P =[-3,-5];%期望极点
%% 2.转换为状态空间
[A,B,C,D]= tf2ss(num,den)
sys0 = ss(A,B,C,D)
%% 3.判断可控和能观
nc =[A,A*B]
rank(nc)
if rank(nc) == rank(A)
disp(‘可控’)
else
disp(‘不可控’)
end
no =[A;C*A]
rank(no)
if rank(no) == rank(A)
disp(‘能观’)
else
disp(‘不能观’)
end
%% 4.极点配置
K = place(A,B,P)
A_hat = A-B*K;
sys = ss(A_hat,B,C,D);
pole(sys)
step(sys)
sss = ss2tf(A_hat,B,C,D)
阶跃响应结果如图4所示。

图4 状态空间极点配置后阶跃响应

图5 状态观测器设计
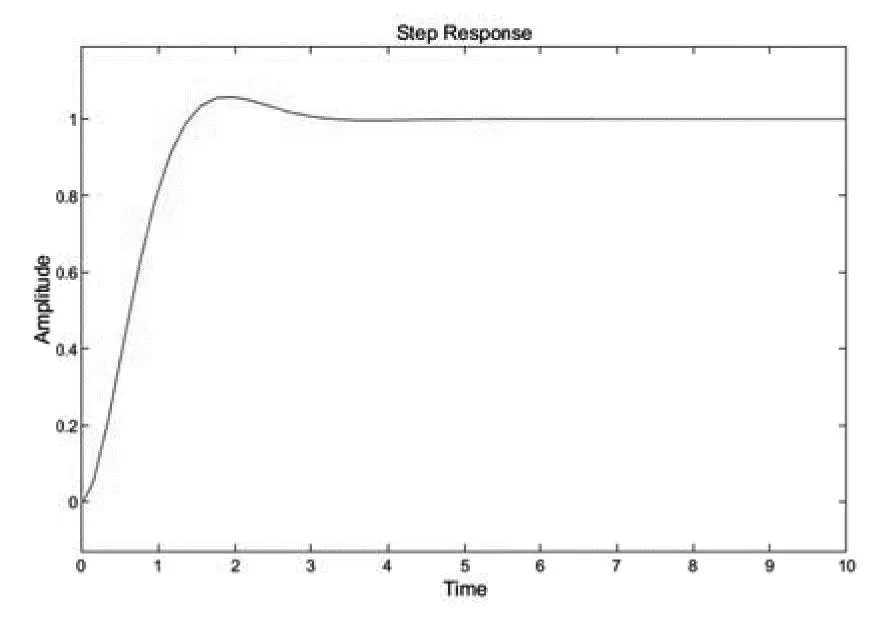
图6 状态空间下的输出
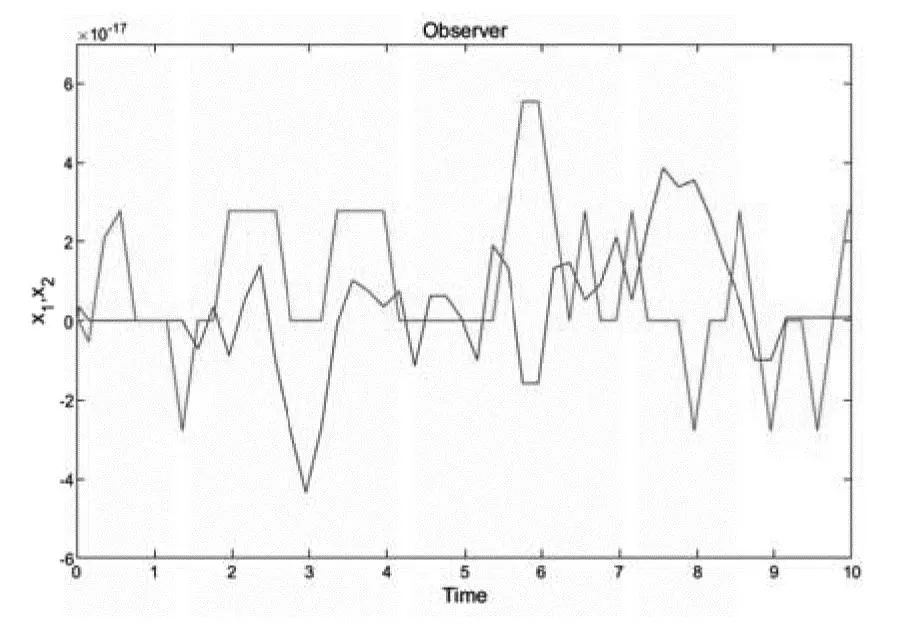
图7 状态观测器观测结果
通过以上讨论可以看出,针对RLC电路可以从课程群的角度将“自动控制原理”和“现代控制理论”无缝连接,从而将不同课程的知识点串在一起,从纵向加深学生对课程的理解。不仅如此,仍然以RLC电路为例,继续深化讨论“智能控制”的案例教学。
3 “智能控制”教学案例
上节从课程群的角度应用RLC案例讨论了“现代控制理论”的知识点,本节仍然以RLC电路为例,讨论“智能控制”的知识点。以“智能控制”中最重要知识点的神经网络控制说明该课程案例教学。
仍然考虑RLC电路,其传递函数为式(4),状态空间方程为式(5),若考虑输出存在未知有界非线性干扰的情况,“自动控制原理”和“现代控制理论”均不好解决。但是在“智能控制”中,处理未知干扰是其基本知识点,可采用模糊、神经网络等多种方法估计未知干扰。
假设未知有界非线性干扰为d(t),将状态空间方程(5)转换为能观能控标准形式为:

(6)
其中
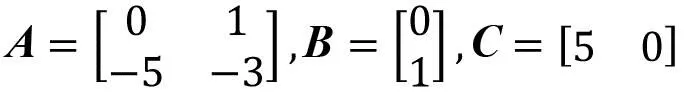
考虑未知干扰的影响,RLC电路的状态空间表达形式为:

(7)
作为教学案例,可以采用“智能控制”中的模糊逻辑估计未知有界干扰,也可以用神经网络估计未知有界干扰,或者都采用后进行对比教学。本文仅采用RBF神经网络估计未知有界非线性干扰,并设计滑模控制器控制RLC电路,补偿未知干扰对电路的影响。
系统模型转换为式(7)后,x1表示电容两端的电压,我们的目标是设计控制输入端ur(t)的电压让输出电压uc(t)不受未知非线性干扰的影响,按照期望的信号输出。假设预先设定的期望信号为uc(t)=sin(t),即x1d=sin(t),则定义误差:
e=x1d-x1
(8)
定义滑模面为:
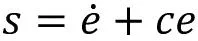
(9)
其中c>0。
根据“智能控制”的内容可以设计控制输入为:

(10)

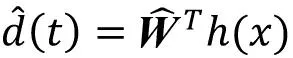
(11)
其中h(x)为RBF神经网络的高斯函数,选择为:
(12)
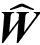
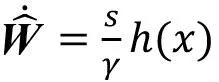
(13)
用Matlab对本案例进行仿真(控制器选择及稳定性证明略,可参考《智能控制》教材或文献[7]),仿真时未知有界非线性干扰选择为d(t)=1.5sin(t)cos(t),c=9,γ=0.05,η=1.1。Matlab仿真程序如图8所示,控制结果,控制输入和神经网络逼近未知干扰结果如图9~11所示。

图8 神经网络滑模控制
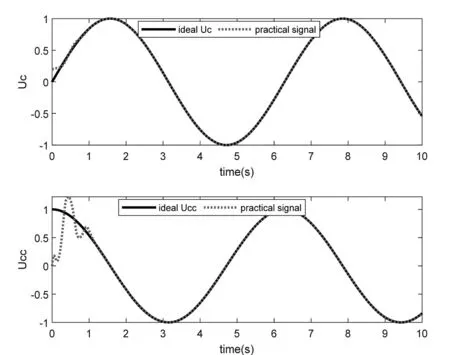
图9 x1,x2的控制输出和预设输出的对比
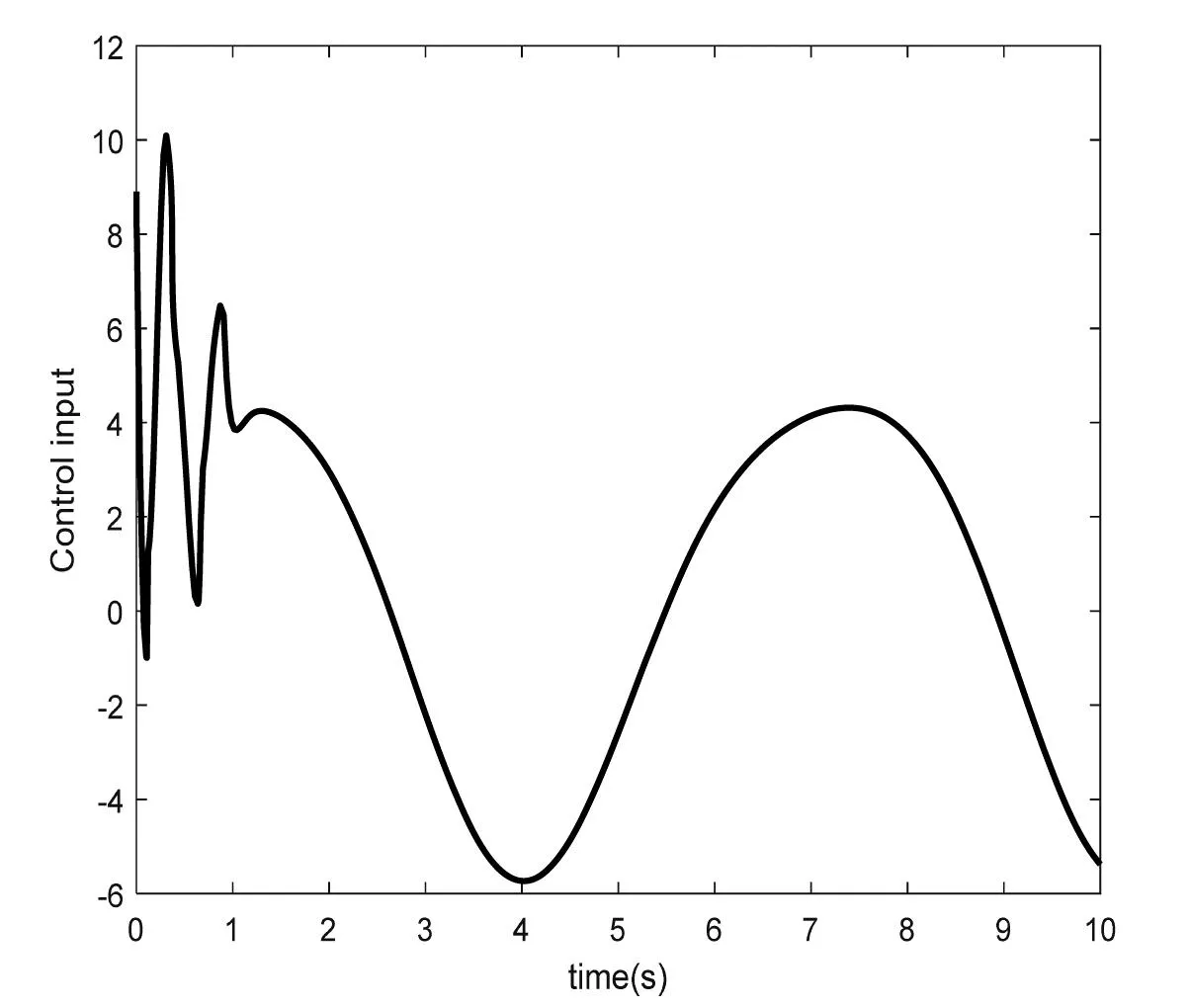
图10 控制输入信号

图11 估计干扰和实际干扰的对比
对“智能控制”课程来说,可以用RLC电路为案例教授并验证模糊控制、神经网络控制和各种进化算法控制的内容。本案例涉及“智能控制”的知识点包括估计未知非线性干扰、神经网络、滑模控制、李雅普诺夫稳定、自适应控制等。如果继续深挖,还可以将更多知识点纳入本案例。从课程群角度看,应用RLC电路从传递函数建模开始到神经网络滑模控制分别串联了“自动控制原理”“现代控制理论”和“智能控制”三门课的多个知识点,有助于学生们从纵向加深对这三门课程知识的理解和掌握。多利用这样的案例可以提高学生的学习兴趣,引导学生将理论和实践结合,更好地学习专业知识。
4 结语
采用RLC电路为案例,从课程群的角度对“自动控制原理”“现代控制理论”和“智能控制”三门课程的主要知识点进行了纵向串联。对RLC电路的传递函数模型建模、极点配置等串联了“自动控制原理”的传递函数模型的建立,零极点配置,根轨迹分析以及冲激和阶跃响应等知识点;通过对RLC电路的状态空间模型转换、状态观测器等串联了“现代控制理论”的传递函数模型和状态空间模型的转换、能控性和能观性判据、状态空间模型下的极点配置以及状态观测器设计等知识点;通过对RLC电路的神经网络滑模控制串联了“智能控制”的神经网络控制、滑模控制、自适应控制,以及“现代控制理论”中的李雅普诺夫稳定等知识点。对于同一个案例,在不同课程中采用课程群的视角可以将各个知识点串联在一起,加深学生们对学习内容的理解和掌握,且案例教学容易实现理论联系实际,切实提高学生分析问题和解决问题的能力,让学生不仅喜欢学,还能学得会、学得好。

