沉管隧道管节拖航过程的运动性态及影响因素研究

贺维国，张金凤，吕 洋，李婧宜，张浦阳

(1.中铁隧道勘测设计院有限公司，天津 300133； 2.西南交通大学 土木工程学院，四川 成都 610031； 3.天津大学 建筑工程学院，天津 300072； 4.天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

沉管隧道因对地质条件要求低、施工工期短、工程造价较低等显著优势[1-2]，目前占据了一定市场并有着广阔的发展应用前景[3]。目前中国已建成上海金山供水隧道、天津海河隧道、宁波甬江隧道及世界最长公路沉管隧道——港珠澳大桥等[4-5]；在建的项目包括大连湾海底隧道[6-7]、深中通道沉管隧道[8]、襄阳东西轴线过江隧道[9]等。随着沉管隧道在实际工程中的应用越来越广泛，沉管隧道管节在浮运过程中的安全性也日益受到关注。徐鹏飞[10]针对香港中环湾仔绕道项目的超大异型沉管管节的远距离海上拖航进行了研究，并根据分析结果获得最优拖航方案；林建军等[11]以佛山东平沉管隧道为研究对象，对管段在干坞内起浮的浮态和初稳性进行分析并得到最佳配载方案；于志安等[12]对管节浮运适应性进行了分析；吴建成[13]以深中通道S08 合同段管节浮运施工为例介绍了管节拖航过程中下沉量分析的数值计算方法；蒋龙皎[14]建立了约束模型和自由模型模拟沉管管段在浅水航道中浮运时的阻力和浮态特性；林鸣等[15]进行了5 次实体管节拖航的试验，观测分析管节的速度及相应的拖航阻力；罗甜[16]针对沉管隧道施工过程中的浮运阶段进行了物理模型试验，获得管节静水拖曳的阻力系数及风浪流复杂因素影响下的浮运拖航缆力；冯海暴[17]采用数值计算和物理模型试验的方法对沉管模型分别在静止和浮运状态时的阻力系数进行分析；沈可[18]采用径向基神经网络对模型试验中沉管管节的水阻力系数进行学习，预报不同水深吃水比和拖航角度的水阻力系数。

然而，目前对沉管隧道浮运的研究主要集中于外海浮运过程，对内河沉管隧道管节浮运风险因素的研究较为有限，特别是对长距离复杂水域中内河沉管隧道管节浮运中的风险考虑不足[19]。随着内河沉管隧道建设的日益增多，沉管在内河中浮运的安全性也愈加受到重视。本文针对内河某实际工程中的沉管隧道管节结构的浮运过程进行研究，并采用改变拖航过程中缆绳布置方式、缆绳绳长、拖船航速及浪向角的方法研究单一变量对沉管浮运过程中运动响应的影响。

1 模型验证及建立

作为一款较为成熟的水动力软件，MOSES 是面向海洋工程的高级分析语言，可以在静态分析、时域分析和频域分析过程中对结构相应的载荷工况展开动力响应分析。首先对MOSES 软件计算沉管拖航模型的准确性进行验证，参考文献[18]中的试验结果，在MOSES 中建立与文献中试验相同的模型，得到不同拖航速度下的拖航阻力如图1 所示。

图1 不同拖航速度下的拖航阻力Fig.1 Towing resistance at various towing speeds

取200 s 以后的平稳段结果与文献中试验结果进行对比，对比结果如图2 所示，可以认为MOSES 数模结果与试验结果吻合较好。

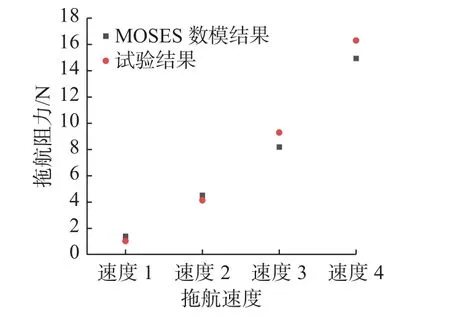
图2 MOSES 数模结果与试验结果对比Fig.2 Comparison between MOSES simulation results and experimental test results

采用某实际工程中的沉管隧道管节原型进行模拟，结构参数为：沉管长102.8 m，宽31.3 m，高8.9 m，重心高3.25 m，质量20 259.2 t。根据实际工程中沉管设计的拖缆点位置，设计了Y 型拖缆方式，利用MOSES 软件建立沉管的拖航模型（图3），分别研究缆绳布置角度、缆绳长度、拖船航速和浪向角等4 种因素对沉管浮运过程中运动特性的影响。缆绳布置角度 α和缆绳长度L如图4 所示。波浪等环境参数按照实际工程现场实测资料选取，水深10 m，波高0.21 m，波浪周期为1.76 s，流速为1.0 m/s，风速为11.82 m/s，风向为横风。与外海浮运相比，内河浮运的水深较浅，波浪条件呈现波高较小且波浪周期较短的特点。

图3 沉管拖航的MOSES 模型Fig.3 Immersed tube towing model of MOSES

图4 缆绳布置示意Fig.4 Towing cable layout

设定标准组工况如下：缆绳布置角度为45°、缆绳绳长120 m、拖船航速为0.51 m/s、浪向角为180°。

2 标准组静稳性及运动响应

对沉管隧道管节模型进行静稳性分析，得到回复力臂曲线，如图5 所示。沉管结构的回复力臂先随着横倾角的增大而增大，到达峰值后减小，回复力臂曲线与横轴的交点为消失角，代表沉管结构保持稳定所能承受的最大倾角，沉管的回复力臂消失角为83°，即当沉管结构倾斜角度大于消失角时，结构变为倾覆力臂，会加速结构的倾覆。

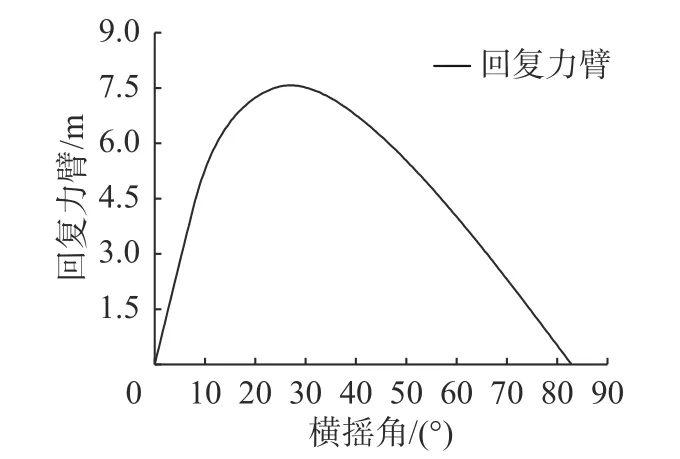
图5 沉管的回复力臂曲线Fig.5 Righting arm curve of immersed tubes

图6 为浮运过程中标准组工况下的沉管重心点纵摇角、垂荡、拖航速度及拖缆力的变化情况。标准组工况下沉管的重心点纵摇角、垂荡、拖航速度及拖缆力峰值分别为0.28°、8 cm、0.49 m/s 和960.9 kN，沉管在浮运过程中的运动响应较小。

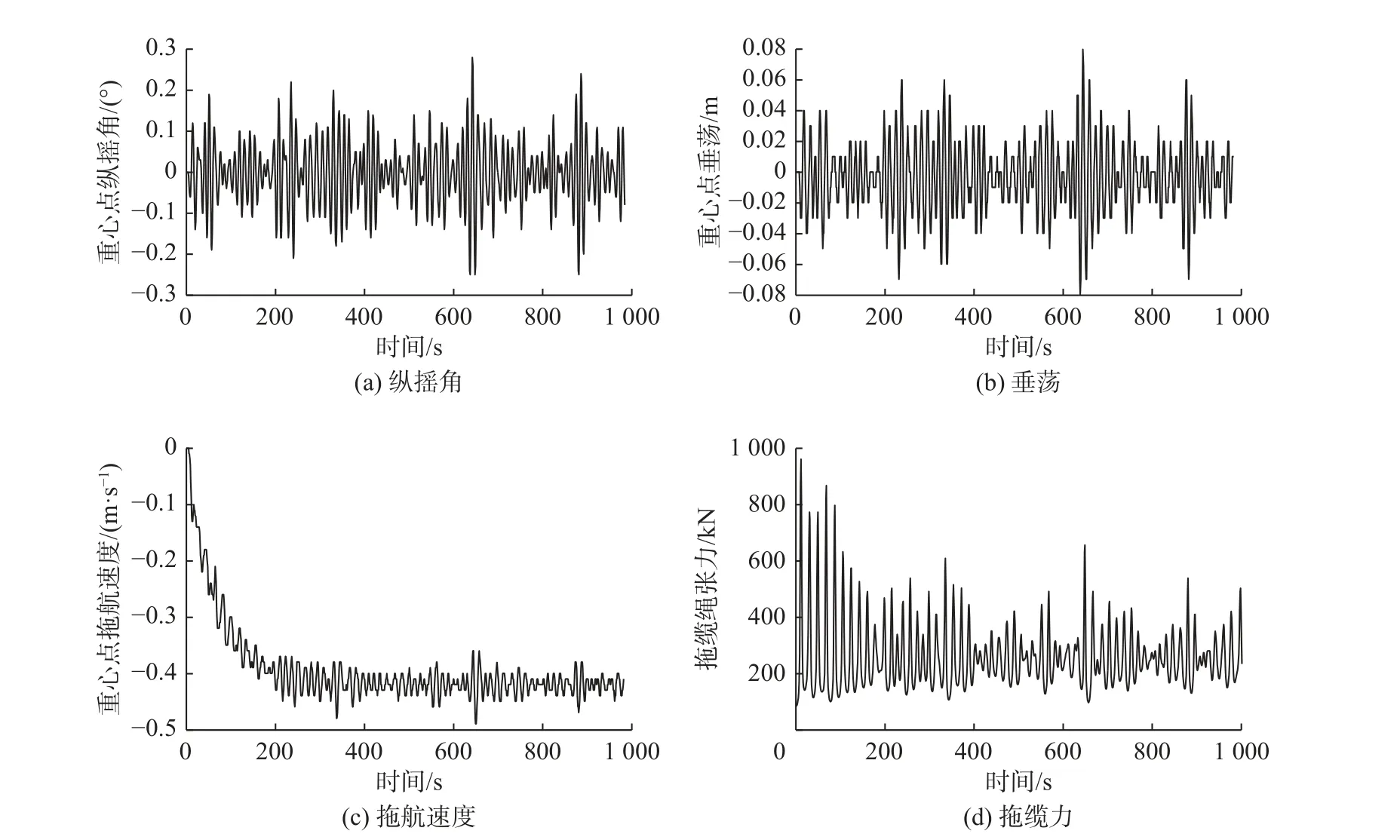
图6 浮运过程中标准组工况下沉管重心点纵摇角、垂荡、拖航速度和拖缆力的变化Fig.6 Variations in pitch angle, heave, towing speed, and center of gravity towing force for the standard group during floating

3 沉管结构拖航稳性及影响因素分析

沉管隧道管节在浮运拖航时需要选择合适的拖航方案，因此需要研究不同因素对沉管结构浮运过程产生的影响。本研究通过控制变量法单独研究各因素对拖航过程的影响，主要考虑缆绳布置角度、缆绳绳长、拖船航速及浪向角对沉管结构拖航稳性的影响，研究工况如表1 所示，其中工况2 为标准组工况。

3.1 缆绳布置角度对结构浮运的影响

为了研究缆绳布置角度对沉管结构拖航稳性的影响，选取30°、45°、60°和75°等4 种角度对沉管结构的浮运过程进行时域分析。给定工况的其他条件为：拖船航速0.51 m/s，浪向角为180°。由于缆绳布置角度改变的同时也会改变缆绳绳长，因此应保证拖船与沉管之间的距离保持不变，尽量减少绳长变化对计算结果的影响。利用MOSES 对4 种不同工况下的沉管结构进行时域分析，得到不同缆绳布置角度下的重心点纵摇角、垂荡、拖航速度及拖缆力时程曲线，如图7 所示。不同缆绳布置角度下的运动响应峰值和均值如表2 所示。可以看出，30°、45°、60°及75°缆绳布置角度下沉管的纵摇峰值均为0.28°，均值约为0°，45°时均值最小，30°时最大；不同布置角度下沉管的垂荡峰值均为8 cm，均值约为0 m，30°时均值最小，45°时最大；拖航速度峰值在30°和45°时均为0.49 m/s，在60°和75°时均为0.48 m/s，差别很小，均值为0.42 m/s；拖缆力峰值在缆绳布置角度30°时最小，45°和60°时相同，75°时最大，均值约为251.7 kN，45°下拖缆力均值最小。可以发现缆绳布置角度对纵摇角、垂荡和拖航速度影响很小，对拖缆力有一定的影响，缆绳布置角度的增大一定程度上能够降低拖缆力的波动幅度。综合各项运动响应，发现缆绳布置角度在45°时纵摇角和拖缆力均值最小，其他运动响应也较小，因此推荐拖航时选择缆绳布置角度为45°。

表2 不同缆绳布置角度下沉管浮运响应峰值及均值对比Tab.2 Comparison of peak and average towing responses of immersed tube for different layout angles

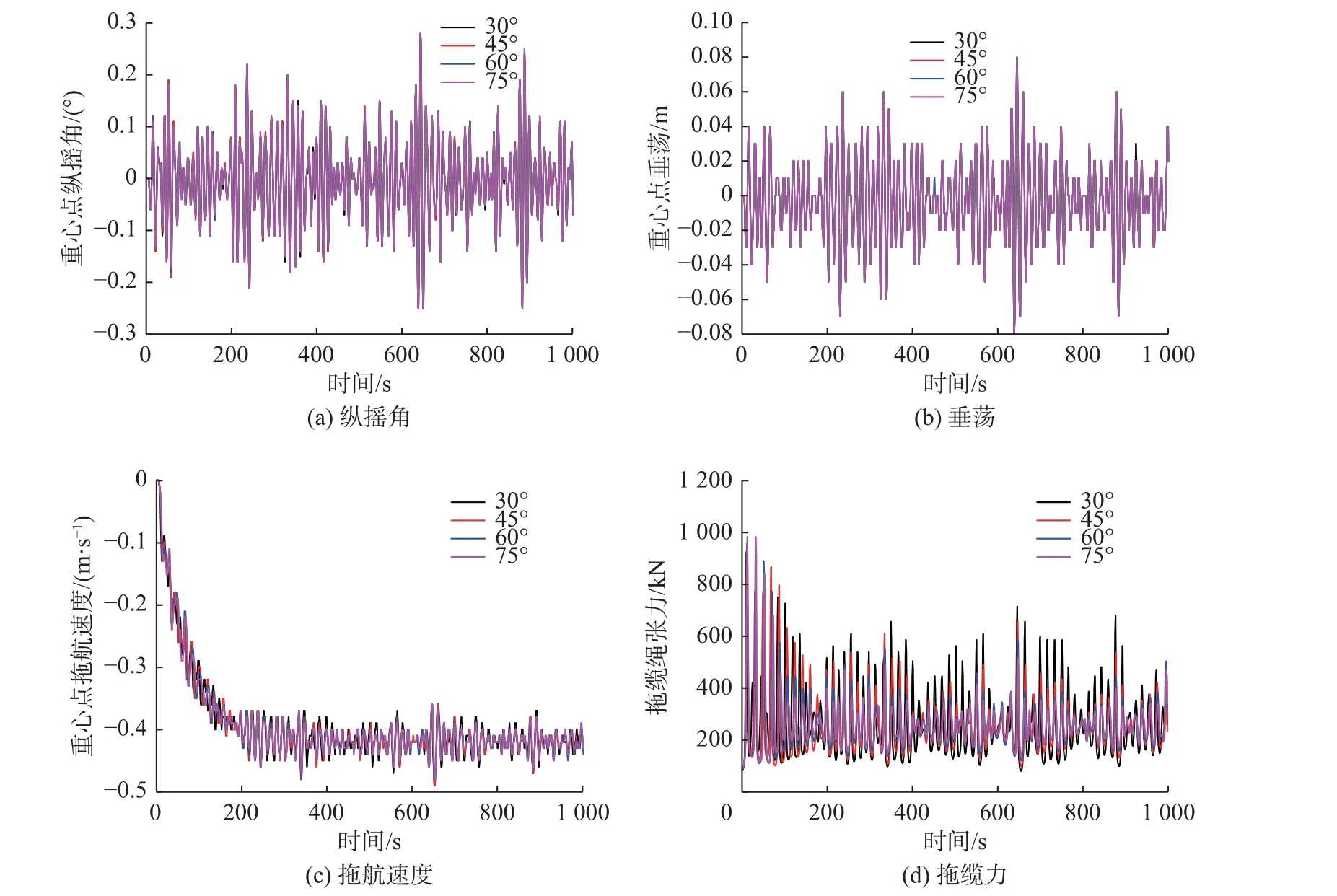
图7 不同缆绳布置角度下的沉管重心点纵摇角、垂荡、拖航速度和拖缆力的变化Fig.7 Variations in pitch angle, heave, towing speed, and center of gravity towing force for different layout angles

3.2 缆绳绳长对结构浮运的影响

缆绳绳长对结构浮运过程中的运动响应也有一定的影响[20]。为了研究缆绳绳长对沉管结构浮运的影响，选取80、100、 120 和140 m 等4 种缆绳绳长，对沉管结构的浮运过程进行时域分析。给定工况的其他条件为：缆绳布置角度45°，拖船航速0.51 m/s，浪向角为180°。不同缆绳绳长下的重心点纵摇角、垂荡、拖航速度及拖缆力时程曲线如图8 所示。

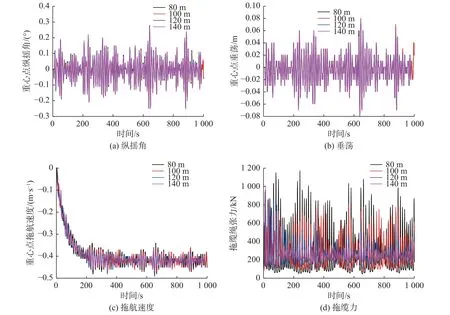
图8 浮运过程中不同缆绳绳长下的沉管重心点纵摇角、垂荡、拖航速度和拖缆力的变化Fig.8 Variations in pitch angle, heave, towing speed, and center of gravity towing force for different cable lengths

不同缆绳绳长下的沉管运动响应峰值和均值的比较见表3。由表3 可见，在浮运过程中，80、100 、120 及140 m 下沉管的纵摇角峰值均为0.28°，垂荡峰值均为8 cm，拖航速度峰值分别为0.48、0.48、0.49 和0.47 m/s，缆绳绳长变化对垂荡和拖航速度均值的影响不明显；说明在逆浪条件下，由于缆绳时刻处于张紧状态，缆绳绳长较短时沉管运动受到约束更大，纵摇角和垂荡响应较小；拖缆力峰值和均值均随着绳长的增大先降低后增大，在80 m 绳长时拖缆力最大，分别在100 和120 m 绳长时对应的峰值和均值最小，观察时程曲线可以发现，拖缆力的变化幅度随着绳长的增大而减小，因此在一定程度上绳长的增大有利于缓解拖船与沉管运动不协调而产生的冲击张力。综合对比各项运动响应结果，80 m 绳长时纵摇角、垂荡和拖航速度均值最小，但拖缆力最大，因此推荐选择100 m 绳长进行拖航。

表3 不同缆绳绳长下的沉管浮运响应峰值及均值对比Tab.3 Comparison of peak and average towing responses of immersed tube for different cable lengths

3.3 拖船航速对浮运的影响

实际工程中需要拖航过程在保证安全的前提下尽量快速完成，因此需要在保证结构稳定的情况下，给定适宜的拖船航速。 为了研究拖船航速对沉管结构浮运的影响，选取了0.26、0.51、0.77 和1.03 m/s 等4 种拖船航速，对结构的浮运过程进行时域分析。给定工况的其他条件为：缆绳布置角度45°，缆绳绳长120 m，浪向角为180°。4 种不同拖船航速下的重心点纵摇角、垂荡、拖航速度及拖缆力时程曲线见图9。

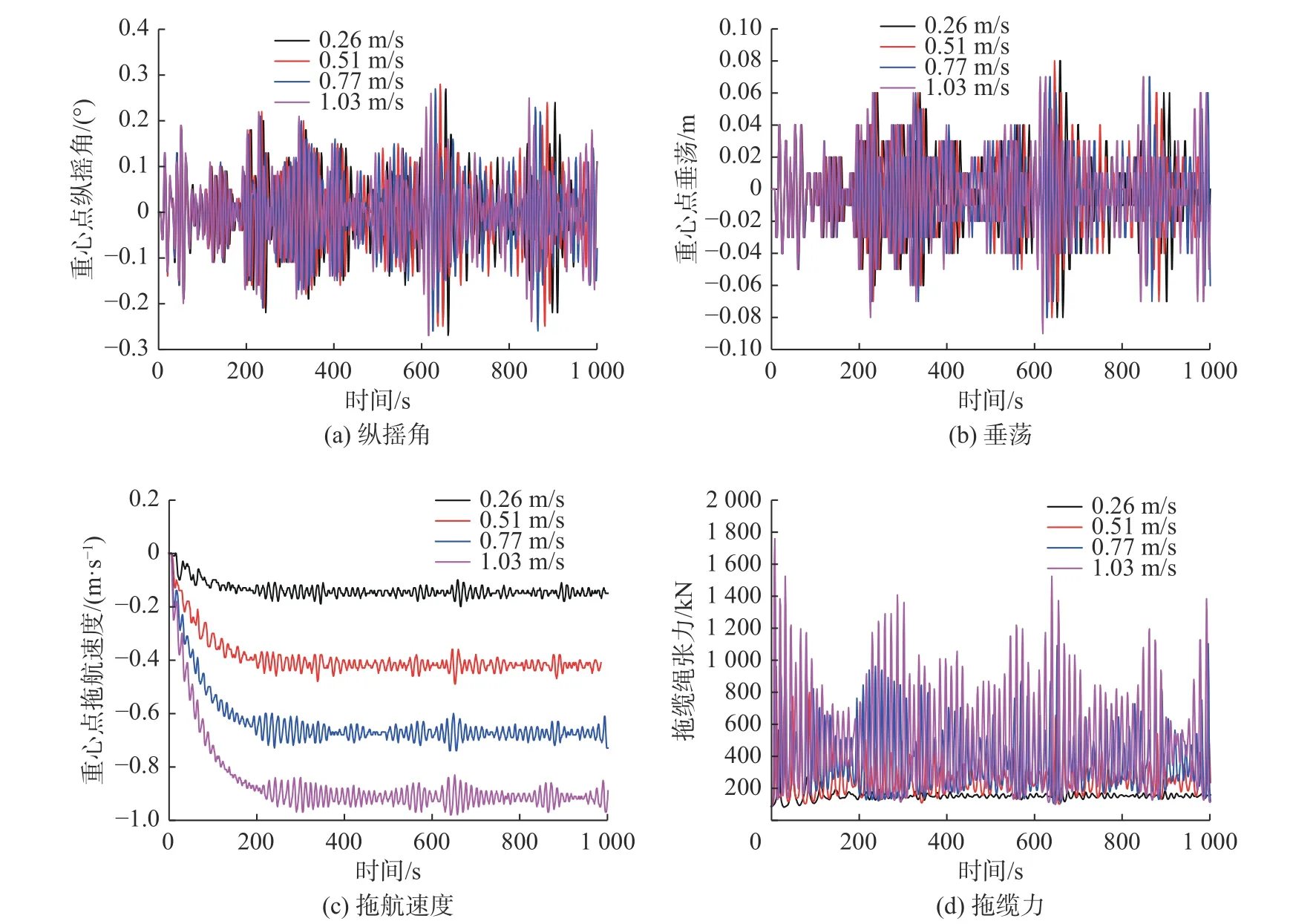
图9 浮运过程中不同拖船航速下的沉管重心点纵摇角、垂荡、拖航速度和拖缆力的变化Fig.9 Variations in pitch angle, heave, towing speed, and center of gravity towing force for different tugboat speeds

不同拖船航速下的沉管运动响应峰值和均值对比如表4 所示。沉管的纵摇角峰值随着拖船航速的增大先增后减，纵摇角均值随着拖船航速的增大而减小，沉管的垂荡峰值在拖船航速为1.03 m/s 时最大，其他拖船航速下峰值相同，均值先降后增；拖航速度和拖缆力的变化趋势一致，其峰值和均值均随拖船航速的增大而增大，且基本呈线性变化。因此为保证浮运过程中的沉管安全稳定，应控制拖船航速不宜过大。由于本工程中缆绳的破断力为3 000 kN，安全系数取2.0，拖缆力不宜超过1 500 kN，因此拖船航速不应超过0.77 m/s。

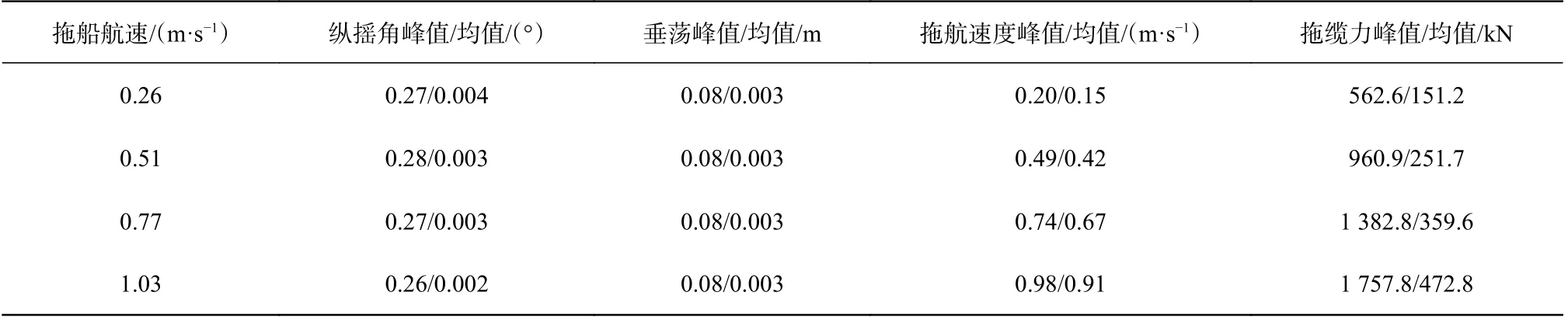
表4 不同拖船航速下的沉管重心点纵摇角、垂荡、拖航速度和拖缆力的变化Tab.4 Variations in pitch angle, heave, towing speed, and center of gravity towing force for different tugboat speeds

3.4 浪向角对浮运的影响

为了研究浪向角对沉管结构浮运的影响，选取0°（顺浪）、45°、135°和180°（逆浪）等4 种浪向角，对结构的浮运过程进行时域分析。给定工况的其他条件为：缆绳布置角度45°，缆绳绳长120 m，拖船航速0.51 m/s 。4 种不同浪向角下的重心点纵摇角、垂荡、拖航速度及拖缆力时程曲线见图10。不同浪向角下的沉管运动响应峰值和均值对比如表5 所示。

表5 不同浪向角下的沉管重心点纵摇角、垂荡、拖航速度和拖缆力的变化Tab.5 Comparison of peak and average towing response of immersed tube for different wave directions

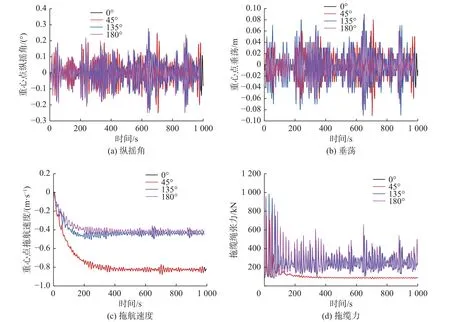
图10 浮运过程中不同浪向角下的沉管重心点纵摇角、垂荡、拖航速度和拖缆力的变化Fig.10 Variations in pitch angle, heave, towing speed, and center of gravity towing force for different wave directions

在浮运过程中，0°和45°下纵摇角峰值均为0.25°，135°和180°下纵摇角峰值分别为0.26°和0.28°，纵摇角均值随浪向角的增大逐渐增大。垂荡峰值在180°浪向角时最小，其余浪向角下均相同，均值在45°浪向角下最小；在逆浪条件下拖航速度明显小于顺浪条件，拖缆力明显大于顺浪条件，且顺浪时拖缆力的波动幅度远小于逆浪。

4 影响因素关联度分析

为更好地量化对比各影响因素与结构拖航响应的关系，利用Apriori 算法基于数模计算结果对沉管结构拖航稳性的各影响因素进行关联度分析，进而分析各因素对结构拖航过程中运动响应的影响。Apriori 算法是经典的关联规则挖掘算法，利用逐层搜索的迭代方法找出数据库中项集的关系[21]。

本文中每个影响因素对应的沉管运动响应都可以认为是1 个项集ai，即

式中：ti为影响因素，包括缆绳角度、缆绳长度、航速和浪向；pij、hij、vij、fij分别表示影响因素ti在时刻j下对应的纵摇角、垂荡、拖航速度和拖缆力。

在Apriori 算法中，主要涉及到支持度S、置信度Cf和提升度L的概念，支持度S（X→Y）是指关联数据X和Y在所有数据中同时出现的概率，即：

式中：Ct(X,Y)为X和Y同时出现的次数；Ct(I)为项的总数。

置信度Cf(X→Y)是指在包含项X出现的项集中，项Y出现的概率，即：

提升度L(X→Y)是指包含项X出现的项集出现项Y的概率与项Y出现的概率之比，即：

提升度反映了项X的出现使项Y的出现概率产生了多大的变化，由于主要研究运动响应与各影响因素的关联度，因此本文通过提升度来判断各因素对结构拖航运动特性的作用大小。

通过支持度、置信度对X、Y之间是否存在关联进行衡量，即X→Y的支持度、置信度大于最小支持度和最小置信度时，认为X和Y之间存在关联。最小支持度和最小置信度阈值越大，得到的关联规则可靠性越高，但是阈值设置过大会导致关联规则数量过少，预期结果易被过滤掉，因此需要对最小支持度和置信度进行反复调试以得到合适的阈值[22]。最终确定最小支持度和置信度为5%。大于等于最小支持度的项集称为频繁项集，频繁项集的基础上大于等于最小置信度称为强关联规则。通过找到各影响因素（X）与运动响应（Y）之间的关联规则，并通过提升度的对比进行关联度分析。提升度大于1 时，说明X对Y有提升作用，且提升度值越大X对Y的提升作用越明显；当提升度小于1 时，说明X对Y有抑制作用，且提升度值越小X对Y的抑制作用越明显；当提升度等于1 时，X与Y无关。

以标准组的运动响应作为依据，取时程曲线中出现的某运动响应值的90%分位数作为该运动响应对应的较大值，得到纵摇角、垂荡、拖航速度和拖缆力的较大值分别为0.13°、0.033 m、0.44 m/s、398.6 kN，将运动响应数据与对应的较大值作比较，根据比较结果将运动响应划分为2 个集合，即{运动响应的绝对值＞较大值}和{运动响应的绝对值≤较大值}，建立影响因素项与{运动响应的绝对值＞较大值}项之间的关联规则，寻找其对应的提升度，并将其作为影响因素对运动响应作用大小的表征值，即当影响因素项对{运动响应的绝对值＞较大值}项的提升度越大时，认为该影响因素对该运动响应的提高作用越明显。各影响因素对运动响应的提升度数值如表6 所示。

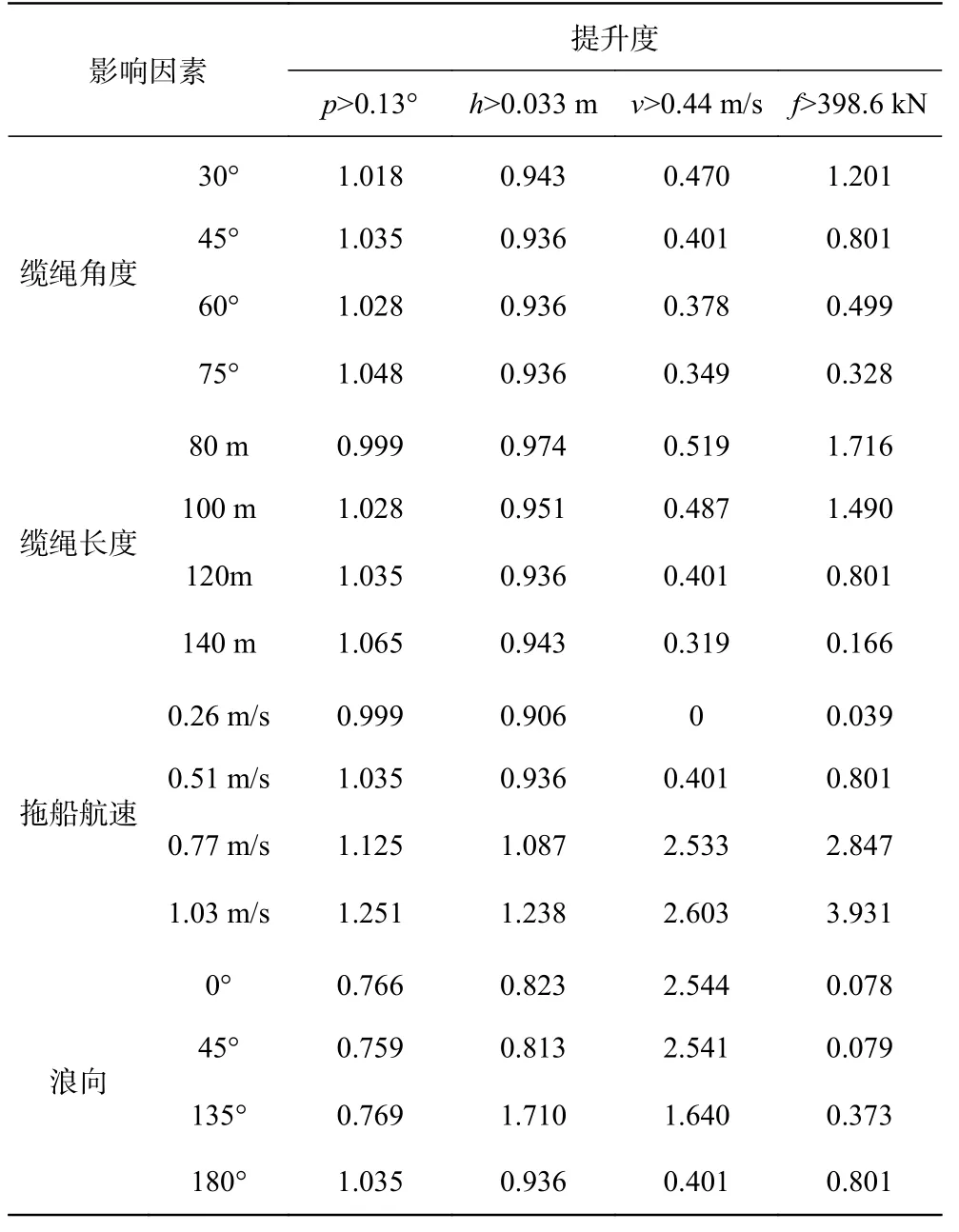
表6 各影响因素对运动响应的提升度Tab.6 Lift degree of influencing factors on motion response

由于各因素的单位不同，将影响因素进行无量纲化处理，无量纲化后各影响因素对运动响应的提升度对比如图11 所示。由图11 可以发现，缆绳角度、绳长和航速均与纵摇角较大值呈正相关，浪向180°与纵摇角较大值呈正相关，其他浪向呈负相关。缆绳角度和绳长的变化对纵摇角的影响较小，航速的变化会引起纵摇角的明显变化，且航速越大，对纵摇角的提升效果越明显。纵摇角对浪向角的敏感度在顺浪和逆浪时表现不同，顺浪条件下纵摇角对浪向的变化敏感性较低，逆浪条件下对浪向更敏感，顺浪45°条件对纵摇角较大值的抑制效果最明显。

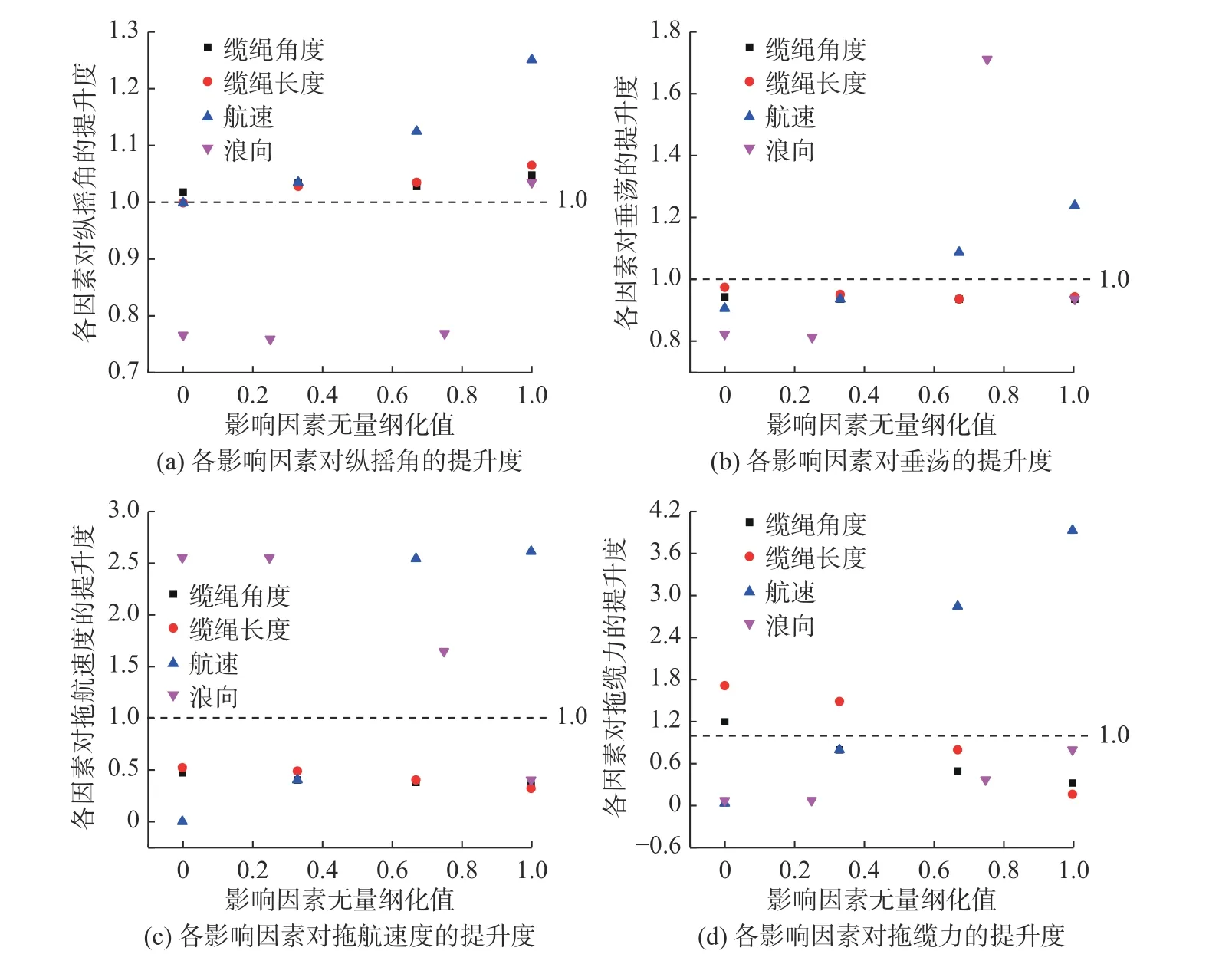
图11 各影响因素对沉管运动响应的提升度对比Fig.11 Comparison of lift degree on towing response of immersed tubes for of different influence factors

缆绳角度和绳长均与垂荡较大值呈负相关，其变化对垂荡的影响不明显；随着航速的增大，航速与垂荡较大值由负相关转为正相关，而浪向与垂荡之间的相关性没有明显规律，顺浪45°条件对垂荡较大值的抑制效果最明显。

缆绳角度和绳长均与拖航速度较大值呈负相关，其变化对拖航速度的影响较小；而航速的增大对拖航速度有明显提升效果，但增大到一定值后提升作用放缓。随着浪向的增大，浪向与拖航速度较大值由正相关转为负相关，这说明逆浪对拖航速度有抑制作用。

各因素变化对拖缆力较大值的提升度均有较为明显的影响，其中拖缆力对航速的变化最为敏感，航速增大对拖缆力的提升效果最明显；浪向对拖缆力较大值的提升度呈负相关，但随着浪向由顺浪转为逆浪，浪向角对拖缆力的抑制作用也逐渐减弱；缆绳角度和绳长的增大均减少拖缆力较大值的出现。

由上述分析可知，沉管结构的运动响应对拖船航速最为敏感，其次是浪向角。结构响应对浪向角的敏感度在顺浪和逆浪时表现不同，顺浪条件下纵摇角、垂荡和拖航速度对浪向的变化敏感性较低，在逆浪条件下对浪向的改变更加敏感，顺浪45°对纵摇和垂荡较大值的抑制效果最好。缆绳布置角度对结构响应的影响最小。各影响因素对沉管运动响应的作用大小为：航速＞浪向角＞缆绳绳长＞缆绳布置角度。结合前文中对响应峰值和均值的分析，在拖航过程中应选择不超过0.77 m/s 的拖船航速，同时推荐顺浪45°进行拖航。

5 结 语

基于某内河实际工程中的沉管隧道管节结构的拖航过程，利用数值模拟的方法研究了缆绳因素、拖船航速和浪向角对沉管结构浮运过程的影响。并利用Apriori 算法对沉管结构拖航稳性的各影响因素进行关联度分析，明确了各因素对结构拖航过程中运动特性的影响程度，得出结论如下：

（1）缆绳角度和绳长对沉管拖航过程中的运动响应影响较小，对拖缆力的影响较为明显，综合对比后认为缆绳布置角度为45°及绳长100 m 时安全性较好。

（2）拖船航速和浪向角对沉管浮运过程中运动响应的影响较为明显。随着航速的增加，结构的纵摇角峰值和平均值降低，拖航速度和拖缆力的峰值及均值则呈线性增长，考虑实际工程中根据拖缆力的要求控制航速应在0.77 m/s 以下；逆浪较顺浪条件下纵摇角增大，拖航速度减小，拖缆力增大，因此在拖航过程中航速不宜过大，尽量避免逆浪拖航。

（3）利用Apriori 算法对各影响因素与运动响应之间的关联度进行了分析，得到各影响因素对沉管运动响应的作用大小为：航速＞浪向角＞缆绳绳长＞缆绳布置角度。因此在拖航过程中应更加关注航速和浪向角对结构响应的影响。