不同温度下带阻尼薄板件振动模态实验与仿真

冯 青， 葛剑敏， 林国斌， 丁叁叁， 朱雷威

（1.同济大学 物理科学与工程学院，上海 200092；2.同济大学 国家磁浮交通工程技术研究中心，上海 201804；3.中车青岛四方机车车辆股份有限公司 国家工程研究中心，山东 青岛 266111）

带有黏弹性阻尼材料的薄板件常用于各类高速交通运载工具的壁板结构，例如飞机舱壁、磁浮车身壁板等，用于减少车厢壁板的振动和辐射噪声。飞机和磁浮等交通运载工具会长期在相对温度较高或较低的极端温度条件下运行，温度对黏弹性阻尼材料的模量、损耗因子会有显著的影响，尤其在低温下，阻尼材料性能大幅衰减，甚至失效，因此，有必要对带有阻尼材料薄板件在大跨度温度范围内的模态特性进行实验，分析温度对带阻尼薄板件振动特性的影响规律。识别黏弹性阻尼材料的材料参数随温度和频率的变化规律，是分析带阻尼薄板构件在极端温度下模态特性的关键。

高铁行业较早开始关注阻尼材料在极端温度条件下的性能，刘佳等［1］对高寒列车常用的4款阻尼材料在低温情况下的性能进行了模态实验研究，发现不同阻尼材料在低温下性能差别显著；陈沛等［2］用仿真方法研究了温度对带阻尼板件隔声特性的影响。由于测试所需的温度环境、方法和设备等因素，带阻尼材料的薄板件在大跨度的温度范围内的振动模态特性还没有系统的测试研究结果。

随着激光测振系统的发展，基于激光多普勒测振原理的测试得到广泛应用。杜鹃［3］使用激光测振技术识别飞机襟翼蒙皮的局部模态；田英等［4］使用二维激光扫描测试装置对热环境下的复合材料层合板进行了振动测试；代江波等［5］非使用三维激光扫描对涡轮叶片的高温模态进行了测试分析。激光测振以其非接触的特点，可以最大程度地减少实体加速度传感器对测试样件带来的附加质量。

对于黏弹性阻尼材料的参数识别主要有DMA（动态力学分析）方法［6］和基于悬臂梁振动的复合损耗因子识别法［7］。DMA 方法对阻尼材料样件加载周期变化的力载荷，将位移响应和力进行处理得到材料在特定受力模式下的储能模量和损耗因子，但要进一步推导黏弹性材料的特性总曲线，过程复杂繁琐。悬臂梁法通过测试带阻尼材料的复合样条和不带阻尼材料的基体样条的频率响应曲线，识别出各阶共振频率和复合损耗因子，再通过公式推导出阻尼材料复模量和损耗因子，误差较大且几乎无法得到连续的黏弹性材料的特性总曲线。基于以上，学者开始尝试倒推法来识别阻尼材料的参数。Ren等［8］基于自由梁的振动频率响应，使用倒推法来识别黏弹性阻尼材料的特性总曲线，该方法在材料级别效果较好，但并未在大尺度构件和仿真中进行验证；Sun等［9］基于带阻尼板件结构的振动响应，使用倒推法识别了阻尼材料在单一温度下的材料频变参数，但并未得到材料的特性总曲线，即无法得到不同温度下的材料参数。

为研究带阻尼薄板件在大跨度温度范围内的模态特性，基于激光多普勒测振原理，在环境箱中使用非接触方法测试各个温度下带阻尼板件的振动响应，分析带阻尼薄板件在极端高、低温下的模态特性以及随温度的变化规律。尝试基于优化算法倒推识别黏弹性阻尼材料的特性总曲线，再从特性总曲线中提取不同温度下的随频率变化的频变参数，用于有限元仿真的输入参数。

1 带阻尼薄板件在高低温下模态特性实验

1.1 高低温下模态实验技术

带阻尼薄板件的模态测试分析需要测试板件上诸多离散点的传递函数，常用方法有加速度传感器配合移动力锤的方法，也有加速度传感器配合激振器的方法。测试件需要放置于温度箱内，移动力锤法操作困难且逐个敲击测点工作量巨大。激振器法需要大量加速度传感器，带来的附加质量会严重影响测试精度。

将激振器和测试样件置于环境箱内，使用基于激光多普勒原理的振动测试技术，以消除加速度传感器附加质量带来的负面影响；同时，环境箱门用透明亚克力板进行封盖，使测试激光可透过透明亚克力板，逐点扫描测试样件上的测点，以满足测试板件在不同温度下各测点的振动响应信号的采集。将激光测振采集的各点传递函数用于模态参数识别，从而得到系统的模态频率、模态阻尼比和模态振型等参数。

激光多普勒测振原理是通过测量从振动物体表面反射回来的激光，通过信号处理解调出多普勒频移fd，从而得到物体振动速率v，进而获得物体的振动特性。其关系式为

式中：λ为激光波长；θ为激光传播方向和振动物体运动方向的夹角。

1.2 高低温下的模态实验过程

测试样件为带有阻尼材料的薄板件，基底板为平直钢板，尺寸500mm×500mm，厚度1.5mm；阻尼材料为高铁车厢内壁使用的水性阻尼浆，单侧涂覆，充分固化后阻尼材料平均厚度3mm。测试板件固定在刚性支座上，连同整个支座置于温度箱中，温度箱正面用透明亚克力板件密封。测试过程中，钢板面朝外，垂直面对激光测试仪。温度箱和激光测振仪的配置如图1所示。

图1 温度箱与激光测振仪Fig.1 Environment chamber and laser vibration meter

带阻尼薄板件的约束状态为对边固支、对边自由。激振器自由悬挂于刚性支座，一同放置在环境箱内。力传感器（图2）粘接到薄板阻尼侧，通过激振杆连接至激振器。力信号作为测试传递函数的参考量引出到数据采集系统中。

图2 传感器和激振器布置Fig.2 Arrangement of transducer and exciter

测试温度为-25℃、-10℃、5℃、20℃、35℃、50℃，将环境箱温度调整至各测试温度点，并且保持30min以上再开始测试，以保证板件阻尼材料内部达到设定的温度。在每个温度下，通过激光测振仪透过透明亚克力板扫描板件上49 个测点（见图1），经FFT 分析得到49 组速率和激振力之间的传递函数用于后续的模态参数识别。

经过预测试，不带阻尼材料的薄板样件的模态参数和有限元仿真一致性较好，因此，认为实验设置是合理的。带阻尼材料的薄板样件在室温环境下前10 阶的模态频率都在300Hz 以下，为确保识别各个温度下的模态参数，并留有一定的余量，频率上限定为1 000Hz。

1.3 模态实验结果分析

将激光扫描得到的各个温度下的49 组传递函数导入Pulse Reflex core软件进行模态参数识别，使用有理分式多项式方法（rational partial polynomial）进行总体拟合［10-11］，提取各个温度下前几阶清晰的模态振型和对应的模态参数。表1 和表2 列出了带阻尼薄板件在各个温度下的前6阶识别出的模态频率和模态阻尼比。

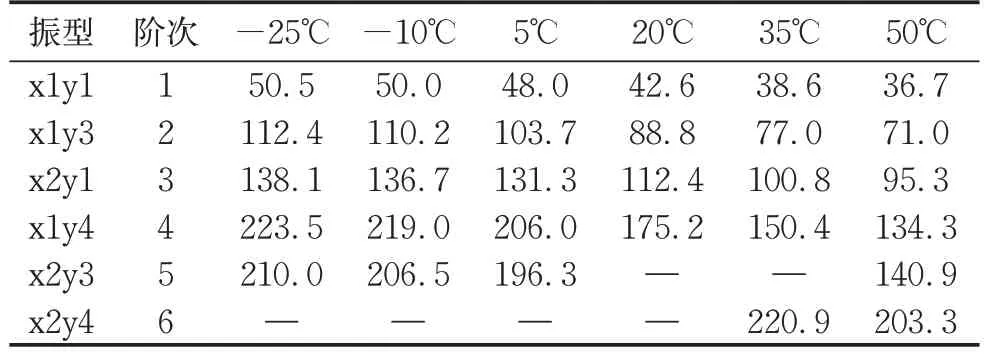
表1 各温度下的模态频率Tab.1 Modal frequency at different temperatures单位：Hz

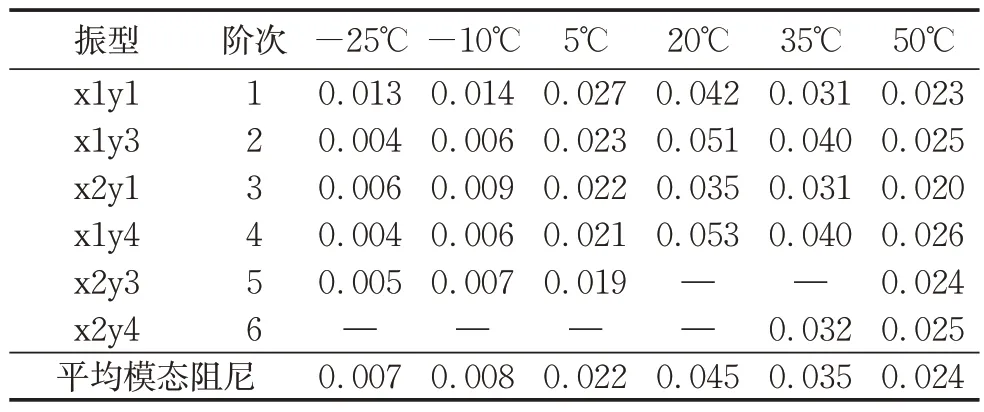
表2 各温度下的模态阻尼Tab.2 Modal damping at different temperatures

在不同温度下带阻尼薄板件前几阶振型基本一致，如图3列出了50℃时的前6阶振型。

图3 前6阶模态振型Fig.3 Vibration modes of first 6 orders

温度对模态频率影响很大，图4 显示为各温度下前4 阶振型的模态频率随温度的变化规律，温度会显著改变带阻尼薄板件的模态频率，且模态频率与温度呈负相关。

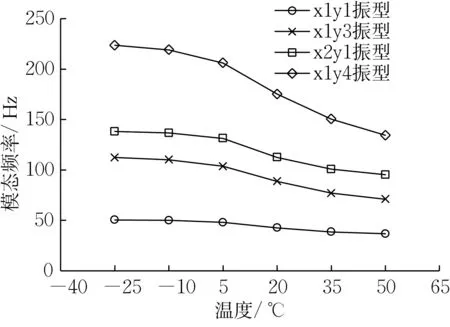
图4 各温度下的模态频率Fig.4 Modal frequency at different temperatures

根据表2 数据，在同一温度下带阻尼薄板件的各阶模态阻尼比基本保持一致。将各个温度下的前几阶模态阻尼比取算术平均值，得到各温度下的平均模态阻尼比，如图5 所示。平均模态阻尼比在20℃时最高，其余温度均呈下降趋势，尤其在-25℃低温时下降尤为显著。

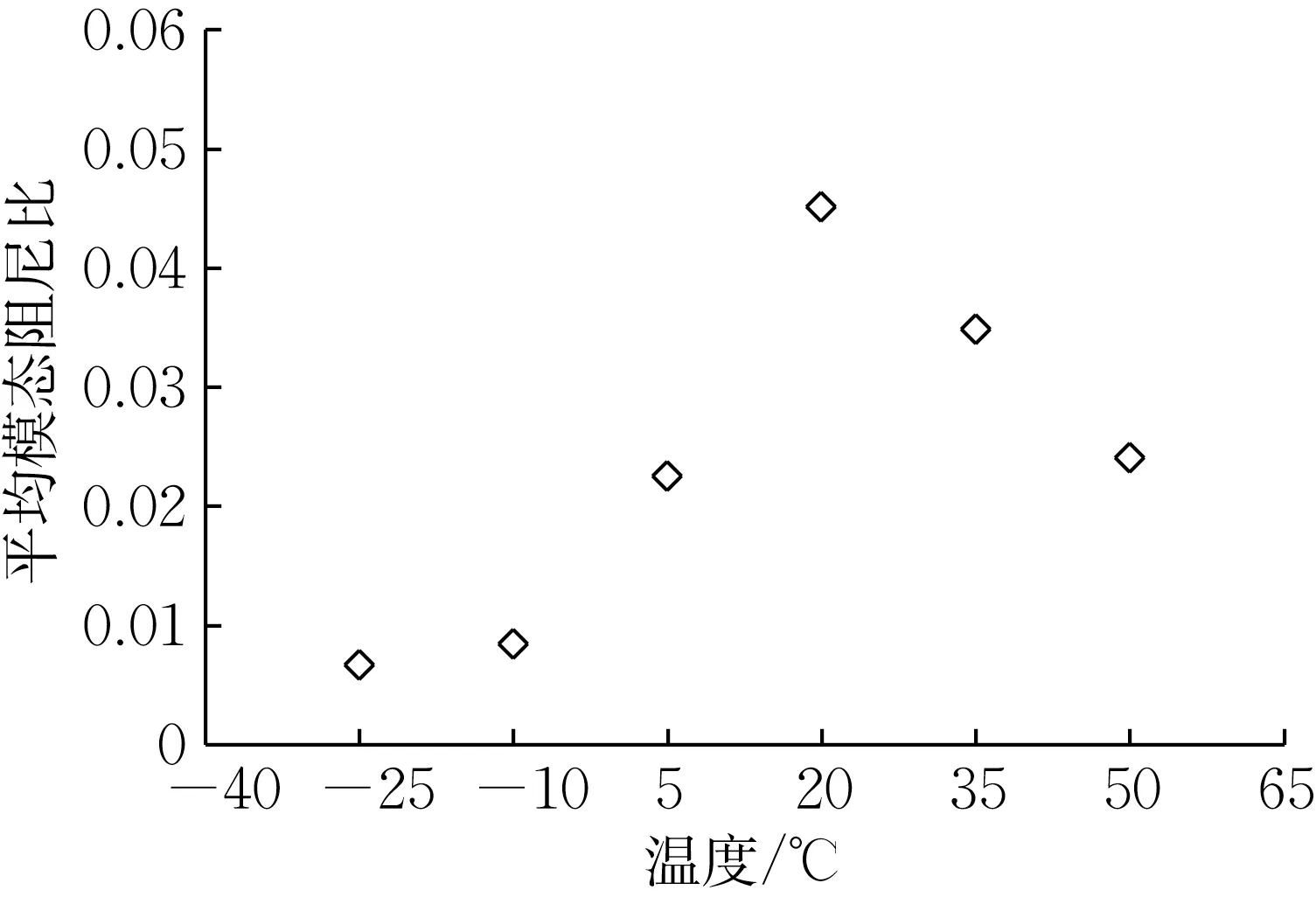
图5 各温度下的平均模态阻尼比Fig.5 Averaged modal damping ratio at different temperatures

2 阻尼材料参数识别

2.1 黏弹材料定常参数识别

2.1.1 复合损耗因子识别

为识别黏弹性阻尼材料在不同温度下的材料损耗因子和模量，首先识别复合样条的复合损耗因子［7］。图6所示是环境箱内的测试装置和样件，悬臂梁测试样件自由长度215mm，宽度10mm，基底梁厚度1mm，阻尼材料厚度3mm。激励位置位于悬臂梁末端，响应位置距固定端64mm，激励和响应信号经采集和处理，可得到振动频率响应曲线，频率上限800Hz。测试温度包括-25℃以及从-20℃到50℃每间隔10℃一个温度点。典型的频率响应曲线包含若干个清晰的共振峰，如图7 中列出的-10℃、20℃和50℃的频率响应曲线。通过第2 阶和第3 阶共振峰的半功率带宽，可识别出对应的频率和复合损耗因子，如表3所示。

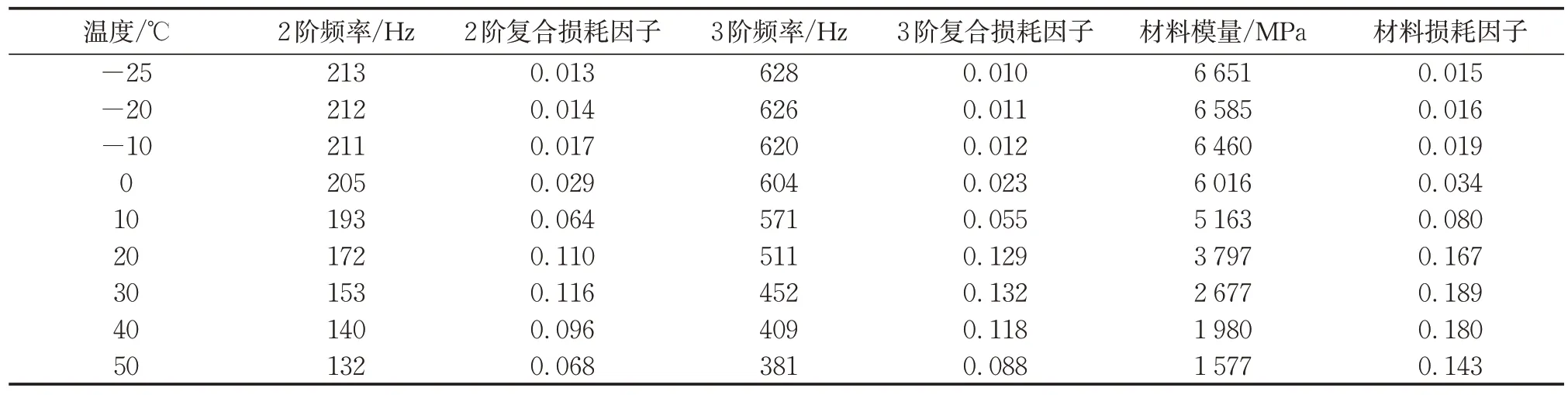
表3 各温度下的损耗因子Tab.3 Loss factor at different temperatures

图6 复合损耗因子测试装置Fig.6 Test configuration for composite loss factor

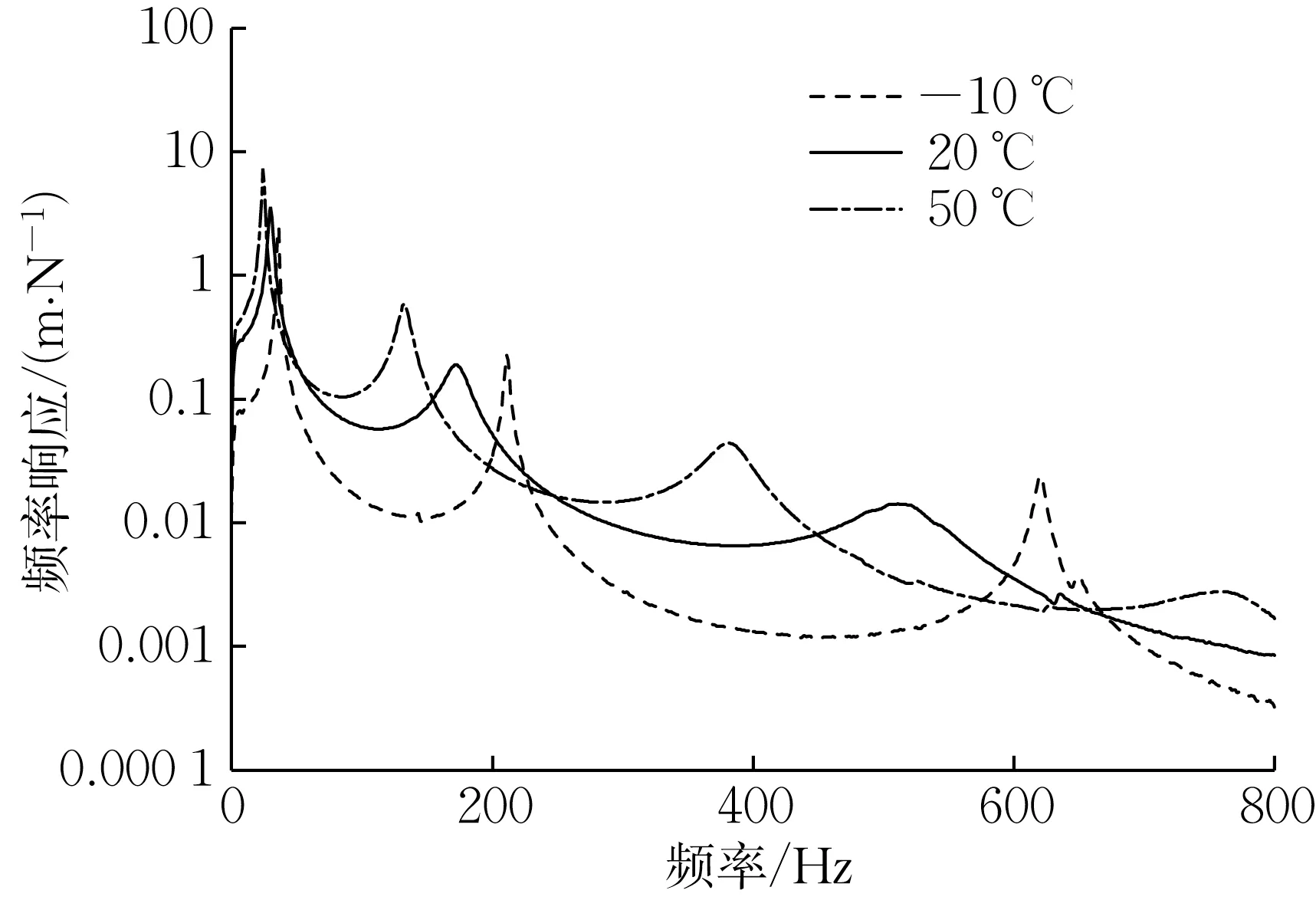
图7 频率响应曲线Fig.7 Frequency response

2.1.2 黏弹材料定常参数

通过式（2）和式（3）［7］可推导阻尼材料的模量E1和损耗因子η1。

式中：ηc为复合样条的复合损耗因子；M为阻尼材料与基底梁材料的模量比；T为阻尼材料与基底梁的厚度比。

根据每一个温度下频率和复合损耗因子可得到对应的材料模量和材料损耗因子，数据如表3所示。每一个温度下，均有一组材料模量和材料损耗因子的不随频率变化的单值参数，可用于后续的仿真参数输入。

2.2 黏弹材料不同温度下频变参数识别

2.2.1 参数识别过程

为识别不同温度下阻尼材料随频率变化的模量和损耗因子参数，首先用包含待定参数的黏弹性材料分数导数模型结合温频转换系数方程，推导不同温度下带频率特性的材料参数。将材料参数代入悬臂梁复弯曲刚度表达式，结合悬臂梁强迫振动理论模型，预测不同温度下的悬臂梁的振动频率响应。将预测的频率响应和测试的频率响应构建目标函数，用Pattern Search（模式搜索）的方法寻找目标函数的最小值，即可找到阻尼材料分数导数模型和温频转换方程的参数，使得预测理论值曲线和实测曲线无限接近，这组参数就是识别出的黏弹性材料的特性参数。识别流程图如图8所示。

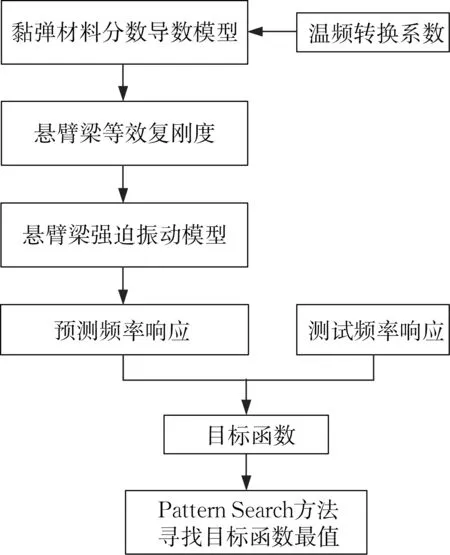
图8 参数识别过程Fig.8 Flowchart of identification

2.2.2 黏弹性材料的分数导数模型

黏弹性材料的参数模型即描述材料动力学性能参数的一组模型公式，以复模量G*表示，如式（4）：

式中：G'为储能模量；G″为损耗模量；η为损耗因子。

考虑复模量G*和频率f以及温度T的相关性，用式（5）所示的4参数分数导数模型［12-13］来描述阻尼材料的特性。

式中：G0为准静态弹性模量；d=G∞G0，其中G∞为动模量的最大值；1τ为损耗模量最大值的频率；β为指数；α(T)为温频转换系数。

2.2.3 温频转换系数

根据温频率等效原理，低温对材料性能的影响与高频的影响等效，高温对材料性能的影响与低频的影响等效，其表达式如式（6）：

经典的温频转换公式［12］如式（7），也称WLF方程。

式中：B、C为待定系数；T0为待定参考温度。因此，利用温频等效原理，如要得到阻尼材料在温度T时的频变参数，只需将α(T)代入分数导数模型即可。

2.2.4 悬臂梁复弯曲刚度

基于文献［14］所述复刚度法推导得到带有自由阻尼的悬臂梁复弯曲刚度B'，如式（8）所示：

式中：B1为基底梁弯曲刚度；e为阻尼材料与基底梁材料的模量比，e=E2E1；h为阻尼材料与基底梁的厚度比，h=H2H1。将式（5）的阻尼材料在温度T时的复模量代入式（8），可得到悬臂梁随频率变化的复弯曲刚度B'。

2.2.5 悬臂梁动力学模型梁弯曲振动运动方程如式（9）：

式中：y=y（x，t）为梁在位置x和时间t的位移；ρ为线密度；B'为梁的复弯曲刚度。应用悬臂梁一端固支一端自由的边界条件，得到悬臂梁的弯曲振动的特征方程如式（10）：

式中：γi=-(sinhλil-sinλil)/(coshλil+cosλil)。

根据图9 所示悬臂梁强迫振动示意图，写出任意点激励任意点响应的运动方程为

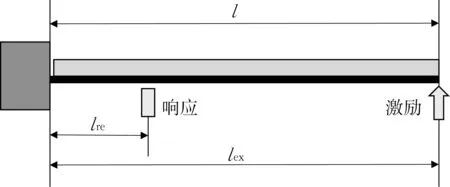
图9 自由阻尼悬臂梁示意Fig.9 Schematics of cantilever beam with free damping

模态质量和模态刚度容易求得。物理坐标中的激励位于距离悬臂梁固定端lex距离处，并设为P0sinθt，因此可得模态坐标下的载荷为

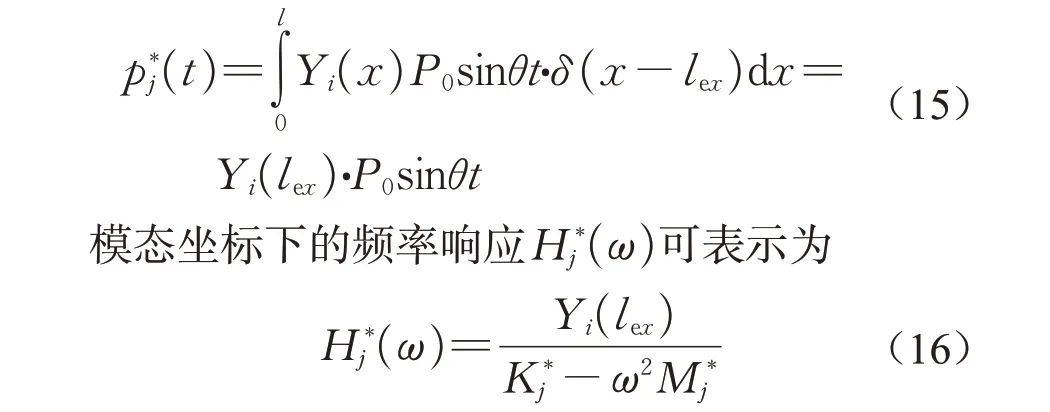
物理坐标下的响应是各阶模态振型的叠加，将响应点位置lre代入，得到物理坐标下的频率响应函数为

根据测试配置，悬臂梁的总长度、激励位置和响应点位置均在模型中体现。各个温度下黏弹性阻尼材料的频变特性也由分数导数模型和WLF 方程得到，已包括在模型之中。因此，此频率响应函数中就包括4 个分数导数模型的变量和3 个WLF 方程的变量。

2.2.6 目标函数

为了使包含有未知量的预测频率响应曲线与实测曲线逼近，使用全局幅值准则［15］，其表达式为

式中：Hx(Tj，fi)和HA(Tj，fi)分别为不同温度下测试和预测得到的频率响应复数值，Hx*和为HA*为复数值的共轭。显然，这个幅值准则同时考虑了频率响应的实部和虚部。因此，构建的目标函数为

拟合问题就变成寻找目标函数J(Tj，fi)最小值问题。使用Matlab 软件中的Pattern Search 全局优化工具，搜索分数导数模型和WLF 方程的7 个变量，使目标函数最小。

2.2.7 黏弹性阻尼材料的特性总曲线

选用了-20℃到50℃的8 个温度下测试所得的频率响应曲线，以及根据待定参数建立的8 组对应温度下的频响预测曲线，构建用于拟合的目标函数，并进行优化拟合。表4给出了优化过程的初始值和约束条件。

表4 优化参数和优化结果Tab.4 Parameters for optimization and results

将表4中的优化结果代入阻尼材料分数导数模型和WLF方程，即可得到黏弹性材料模型如式（20）和式（21）所示表达式，变量为温度T和频率f。

式中：α(T)f为折算频率；G*(f)为材料复模量。

以折算频率α(T)f作为横轴，以材料模量和损耗因子为纵轴，得到黏弹性材料的特性总曲线，如图10 所示。储能模量随折算频率提高而提高，损耗模量和损耗因子存在明显的峰值，在峰值两边会有明显的下降。温频转换系数如图11所示。

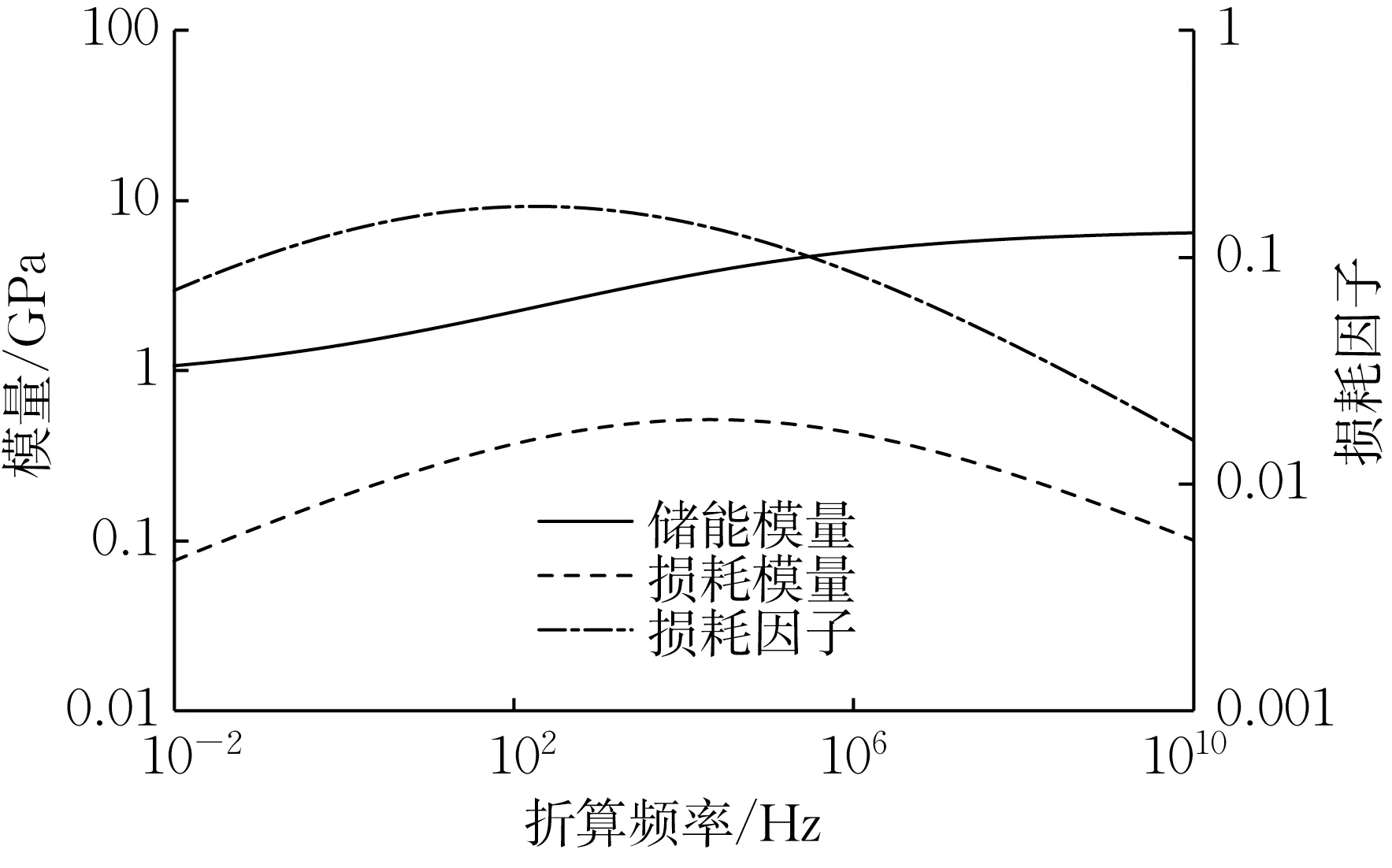
图10 黏弹性材料特性总曲线Fig.10 Nomogram of visco-elastic material

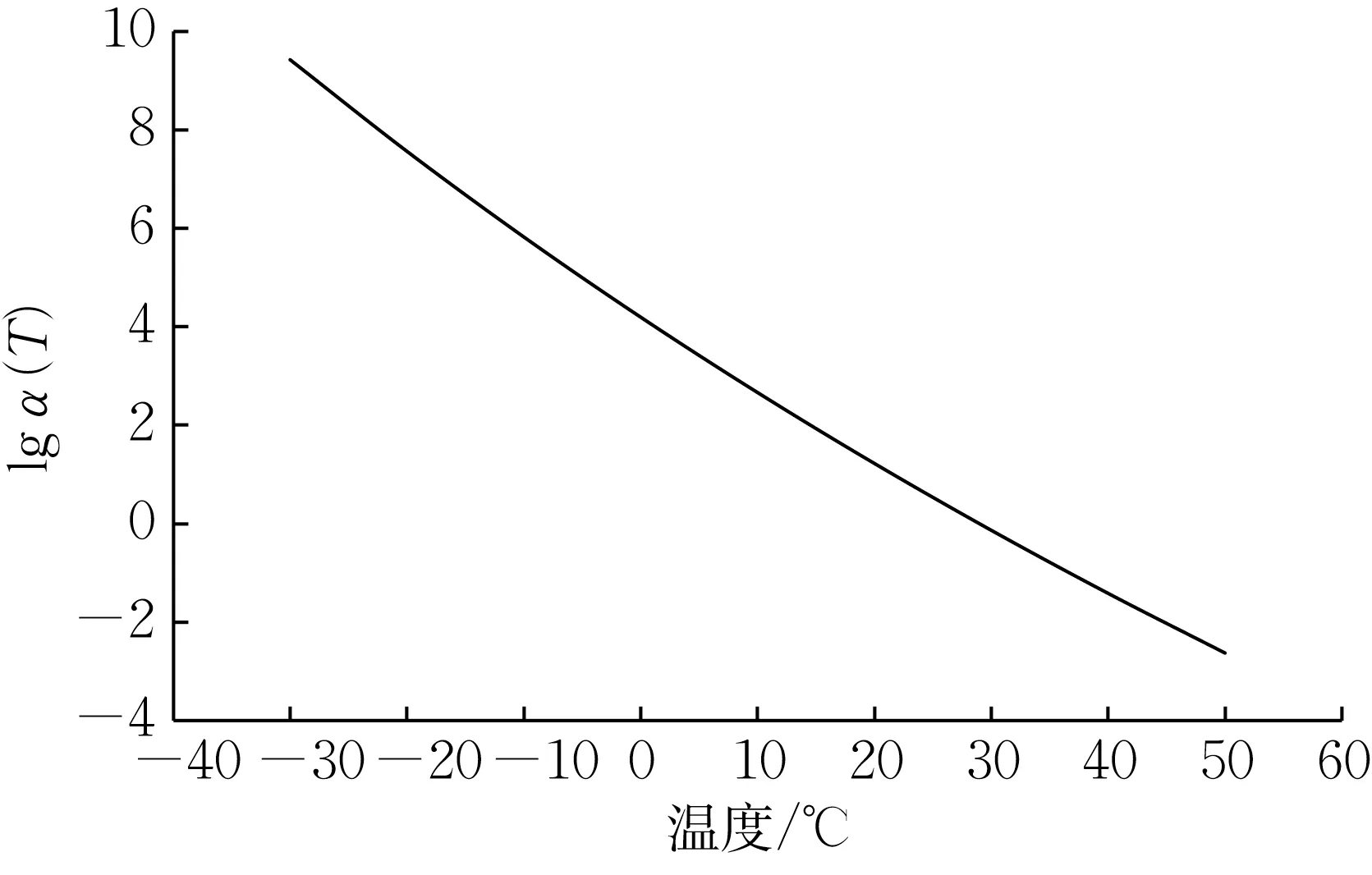
图11 温频转换系数Fig.11 Frequency-temperature shift factor

2.2.8 黏弹性阻尼材料的频变参数

将任意温度T代入WLF 方程得到温频转换系数α(T)，将其代入阻尼材料分数导数模型，即可得到对应温度下自变量为f的材料复模量，根据式（4）材料损耗因子亦可得。图12给出了-25℃、-10℃、20℃和50℃温度下阻尼材料储能模量和损耗因子的频变特性曲线。

材料储能模量在1 000Hz范围内变化相对平缓，总体趋势是频率增加、储能模量提高。损耗因子显示出更显著的频变特征，20℃时损耗因子中间高两头低，-25℃和-10℃时是由高到低的趋势，50℃时是由低到高的趋势。因此，在研究带阻尼薄板件振动响应时，需要充分考虑阻尼材料损耗因子的频变特性。

3 带阻尼板件高低温下振动响应仿真分析

3.1 有限元分析中阻尼材料参数设置

3.1.1 阻尼材料单值参数的设置有限元分析中的频率响应分析模型可表述为

式中：M为质量矩阵；B为黏性阻尼矩阵；K为刚度矩阵；x(ω)为位移响应；F(ω)为载荷。黏弹性阻尼材料单值参数包含在复刚度矩阵K内，表达式

式中：g为总体结构损耗因子；K0为总体刚度矩阵；gE为黏弹性材料的损耗因子；KE为黏弹性材料的刚度矩阵。

3.1.2 阻尼材料频变参数的设置

阻尼材料频变的储能模量G'(f)和损耗模量G''(f)需要根据式（24）和式（25）分别转成频变的数据卡TR(f)和TI(f)，并写入到TABLED1 数据卡中，最终通过SDAMP控制卡调取使用。

式中：gREF为参考损耗因子；GREF为参考模量；G'(f)为材料频变储能模量；G″(f)为材料频变损耗模量。因此，黏弹性材料的频变参数包含在式（26）所描述的刚度矩阵内。

式中：KV为黏弹性材料的刚度矩阵。

3.2 频率响应的有限元验证

使用oSH 模型［16］（偏置壳单元加六面体单元方法）建立带阻尼薄板件的有限元模型，可达到较高的有限元建模和仿真精度。具体地，薄板用四边形壳单元，厚度1.5mm，使用钢材典型材料参数，如表5所示。阻尼材料使用六面体单元，与薄钢板壳单元在交界面处共节点。薄板壳单元偏置0.5倍的钢板厚度。建立的有限元模型如图13所示，约束条件与1.2节中所述实验一致，即对边自由、对边固支；激振点和49个响应点也与实验一致。

根据3.1.1 所述的方法和表3 中对应温度下的阻尼材料模量和损耗因子，在模型中设置阻尼材料的单值参数。根据3.1.2 所述的方法，将图13 所示的不同温度下的频变模量和损耗因子转换成对应的TR(f)和TI(f)，在模型中设置阻尼材料的频变参数。使用直接频率响应法分析带阻尼薄板件的振动响应，分析频率上限为1 000Hz，频率间隔1Hz。在模态实验己有的温度点中，选择-25℃、-10℃、20℃和50℃这几个典型且温度跨度较大的温度点，使用其对应温度下的单值和频变参数进行仿真验证。

3.3 分析结果

图14 所示为-25℃、-10℃、20℃和50℃下激振点和响应点之间频率响应曲线，包括测试结果、单值参数和频变参数仿真所得的结果。2 种参数得到的仿真曲线与测试曲线都有较好的一致性，相比之下，频变参数得到的前几阶频率和幅值更接近测试值。

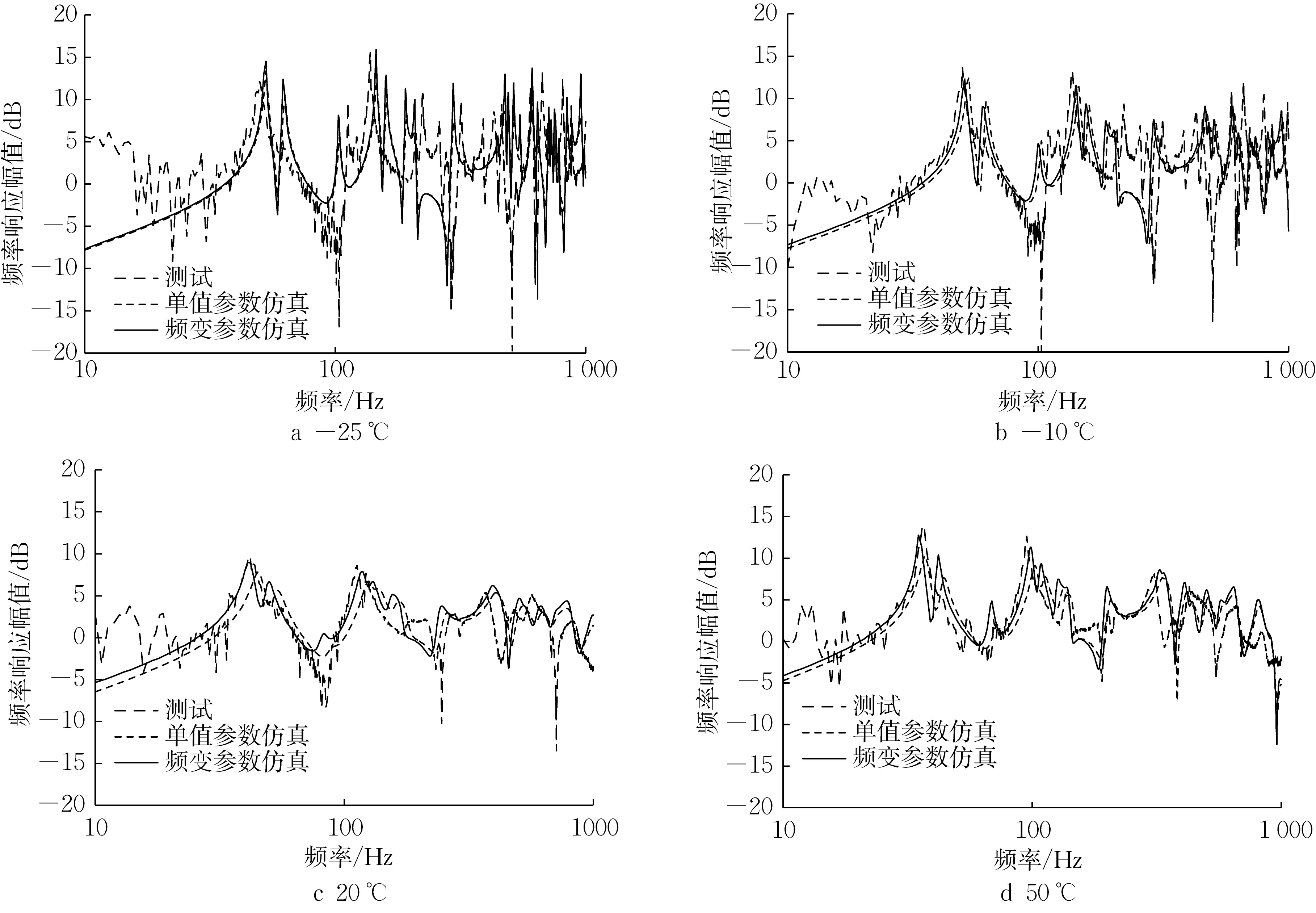
图14 频率响应曲线Fig.14 Frequency response

将图14所示频率响应曲线的前2阶峰值的频率和幅值取出，进行误差分析，如表6所示。单值参数和频变参数仿真得到的1阶峰的频率值最大误差分别为3.0Hz和3.0Hz，2阶峰值的频率值最大误差分别为17.8Hz 和7.9Hz；单值参数和频变参数仿真得到的1阶幅值最大误差分别为11.9dB和5.3dB，2阶幅值最大误差分别为-20.9dB和2.8dB。使用频变参数进行仿真得到前2阶的峰值频率和幅值均比单值参数误差更小，更接近测试结果。因此，本文基于优化算法的倒推法识别得到的频变参数，由于考虑了参数随频率的变化，可以更准确地用于带阻尼薄板件的振动响应仿真分析。

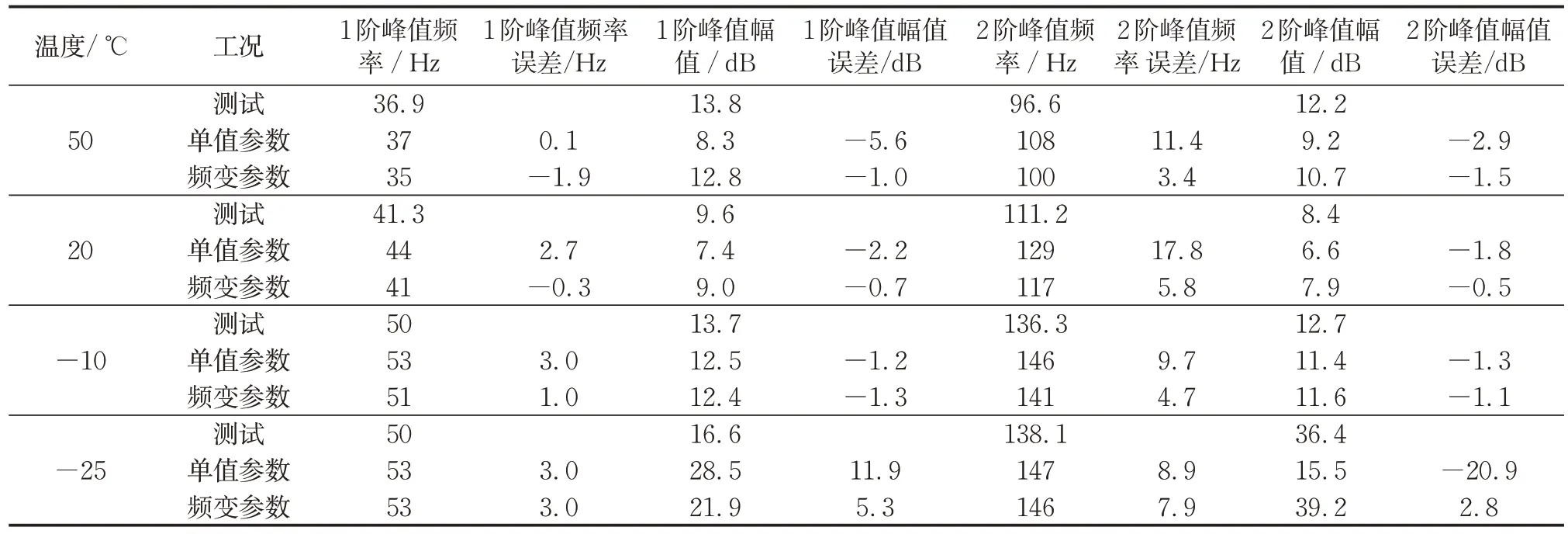
表6 仿真结果的误差分析Tab.6 Error analysis of simulation results

4 结语

对带阻尼薄板构件在大跨度的温度范围内进行了模态参数识别，分析结果表明温度对带阻尼薄板件的模态特性会有显著的影响。温度与模态频率呈负相关，在极端高、低温下，模态阻尼比会有极大的衰减。

提出了基于优化算法倒推识别黏弹性阻尼材料的特性总曲线，再从特性总曲线中提取不同温度下的随频率变化的材料模量和损耗因子。材料的模量随频率的提高而提高，材料损耗因子在不同温度下都呈现明显的频变特性，且趋势各不相同。

将频变参数用于有限元仿真，分析结果显示，频变参数能更准确地预测带阻尼薄板件的振动响应，其频率响应曲线前2阶的频率和幅值的精度比单值参数更高。

作者贡献声明：

冯 青：提出研究内容和研究方法，实施试验和仿真，起草与修订论文。

葛剑敏：确认研究内容和研究方法，指导试验方案，修订论文。

林国斌：指导试验方案，参与修订论文。

丁叁叁：确认研究内容和研究方法，参与修订论文。

朱雷威：参与试验和仿真，协助分析数据。