变中不变找规律 函数特值试一试
——对中考一类定值问题的探究
陈 通
(江苏省泗洪县洪泽湖路实验学校,江苏 泗洪 223900)
在一个给定的图形中,某些元素(如点、线、角、三角形等)按照一定的规律在运动变化,而在运动变化中,某几何量或几何量间的关系(如线段的长度、角的度数、图形的周长或面积的大小等)却始终保持固定的数值,这就是几何图形“变中不变”问题, 也称“定值”问题[1].求解这类“定值问题”难度较大,解决的办法一般是将问题特殊化,即先从特殊情况入手,找出定值,然后再一般化处理.
定值问题常见的题型有:线段、角度定值;周长定值;面积定值;线段的乘积定值等[2].比如,对于线段乘积为定值的问题,大多采用相似法,通过相似成比例把乘积问题转化为比例问题.此外,对于定值问题,还可以设变量x,并用x的代数式来表示其他变量,通过代数式变形计算解决问题.若计算结果中不含x和其他变量,则为定值,否则不是.这种用 “数” 来研究 “形” 的方法,是研究定值问题的常用方法[3],同时体现了转化思想与数形结合思想.
1 三角形中的定值问题


图1 例1题图 图2 例1解析示意图


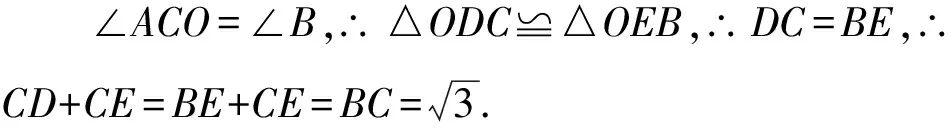
点评本题是一个选择题,我们可以通过点E的特殊位置快速选出答案.对于解答题探究定值,一般是先考虑特殊情况,得到定值,再一般化,确定求证途径.
2 圆中的定值问题
例2如图3,线段AB是⊙O的直径,延长AB至点C,使BC=OB,E是线段OB的中点,DE⊥AB交⊙O于点D,P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC.
(1)求证:CD是⊙O的切线.



图5 例2(1)问解析示意图
点评解决定值问题时,对于一些与定点、定长等有关的定值问题,定值一定和题目所给的“不变量”有关.因此,在“变化”的量中寻求“不变”的量是解决问题的关键.一般可先从特殊位置、极端位置或特殊数值入手,探究出这个定值,然后再借助特殊情况的思路作为探讨一般情况的基础,完成一般情况的证明.
3 矩形中的定值问题
例3如图6,在边长为3的正方形ABCD中,点E是CD边上一点,点F是CB延长线上一点,AF=AE,连接EF,交AB于点K,过点A作AH⊥EF于H,延长AH交BC于点G,连接HD,若BG=2,则AK·DH=____.


图6 例3题图 图7 例3解析示意图



点评根据正方形和三角形的性质以及一般角的三角函数值等,找出AK=FG,从而可得3-2x=2+3x是解题的关键.
4 平行四边形中的定值

分析本题主要考查了平行线之间的距离和等边三角形的判定和性质,先证明△ABE是等边三角形,再在AD上取点Q,使AQ=AN,构造△AQP≌△ANP(SAS),将折线线段和转化为平行线之间的距离,得出M、P、Q在同一直线上,并且PQ⊥BC,通过解三角形求出AP.
对于一些与定点、定长等有关的定值问题,可以将问题引向特殊情形,先求出这个定值, 再进行证明,探索出的定值必须通过证明才能明确其正确性,要论证的问题就是特殊情形与一般情形的固定关系.也可直接设参数进行推理、计算,并在计算中消去参数,得到定值.得到了定值,做题时就有了明确的目标与方向,再证明一般情况下结论成立即可.

